Lời Giải Toán Phổ Thông
Hướng dẫn giải bài tập Toán phổ thông chương trình 2018. Chia sẻ đề và lời giải đề thi thử các tỉnh thành, đề thi chính thức THPTQG, đề thi Đánh giá năng lực ĐHQG TPHCM
Toán 8
Toán 8 - Chân trời sáng tạo
Chương 1. Biểu thức đại số
Chương 2. Các hình khối trong thực tiễn
Chương 3: Định lý Pythagore. Các loại tứ giác thường gặp
Chương 4. Một số yếu tố thống kê
Hoạt động thực hành và trải nghiệm
Chương 5. Hàm số và đồ thị
Chương 6. Phương trình
Chương 7. Định lý Thalès
Chương 8. Hình đồng dạng
Chương 9. Một số yếu tố xác suất
Hoạt động thực hành và trải nghiệm
Toán 8 - Kết nối tri thức
Chương 1. Đa thức
Chương 2. Hằng đẳng thức đáng nhớ và ứng dụng
Chương 3. Tứ giác
Chương 4. Định lý Thales
Chương 5. Dữ liệu và biểu đồ
Hoạt động thực hành và trải nghiệm
Chương 6. Phân thức đại số
Chương 7. Phương trình bậc nhất và hàm số bậc nhất
Chương 8. Mở đầu về tính xác suất của biến cố
Chương 9. Tam giác đồng dạng
Chương 10. Một số hình khối trong thực tiễn
Hoạt động thực hành và trải nghiệm
Toán 8 - Cánh diều
Chương 1. Đa thức nhiều biến
Chương 2. Phân thức đại số
Hoạt động thực hành và trải nghiệm Chủ đề 1. Quản lí tài chính cá nhân
Chương 3. Hàm số và đồ thị
Chương 4. Hình học trực quan
Hoạt động thực hành và trải nghiệm Chủ đề 2. Thực hành tạo Hologram.
Chương 5. Tam giác. Tứ giác
Chương 6. Một số yếu tố thống kê và xác suất
Chương 7. Phương trình bậc nhất một ẩn
Chương 8. Tam giác đồng dạng. Hình đồng dạng
Hoạt động thực hành và trải nghiệm Chủ đề 3. Thực hành đo chiều cao.
Toán 9
Toán 9 - Chân trời sáng tạo
Chương 1: Phương trình và hệ phương trình
Chương 2: Bất đẳng thức. Bất phương trình bậc nhất một ẩn
Chương 3: Căn thức
Chương 4: Hệ thức lượng trong tam giác vuông
Chương 5. Đường tròn
Chương 6. Hàm số y = ax² (a khác 0) và phương trình bậc hai một ẩn
Chương 7. Một số yếu tố thống kê
Chương 8. Một số yếu tố xác suất
Chương 9. Tứ giác nội tiếp. Đa giác đều
Chương 10. Các hình khối trong thực tiễn
Hoạt động thực hành và trải nghiệm
Hoạt động thực hành trải nghiệm
Toán 9 - Kết nối tri thức
Chương 1. Phương trình và hệ hai phương trình bậc nhất hai ẩn
Chương 2. Phương trình và bất phương trình bậc nhất một ẩn
Chương 3: Căn bậc hai và căn bậc ba
Chương 4: Hệ thức lượng trong tam giác vuông
Chương 5. Đường tròn
Hoạt động thực hành trải nghiệm
Chương 6. Hàm số y = ax² (a khác 0). Phương trình bậc hai một ẩn
Chương 7. Tần số và tần số tương đối
Chương 8. Xác suất của biến cố trong một số mô hình xác suất đơn giản
Chương 9. Đường tròn ngoại tiếp và đường tròn nội tiếp
Chương 10. Một số hình khối trong thực tiễn
Hoạt động thực hành trải nghiệm
Toán 9 - Cánh diều
Chương 1: Phương trình và hệ phương trình bậc nhất
Chương 2. Bất đẳng thức. Bất phương trình bậc nhất một ẩn
Chương 3. Căn thức
Chương 4. Hệ thức lượng trong tam giác vuông
Chương 5. Đường tròn
Chương 6. Một số yếu tố thống kê và xác suất
Chương 7. Hàm số y = ax² (a ≠ 0). Phương trình bậc hai một ẩn
Chương 8. Đường tròn ngoại tiếp và đường tròn nội tiếp
Chương 9. Đa giác đều
Chương 10. Hình học trực quan
Toán 10
Toán 10 - Chân trời sáng tạo
Chương 1: Mệnh đề và tập hợp
Chương 2: Bất phương trình và hệ bất phương trình bậc nhất hai ẩn
Chương 3: Hàm số bậc hai và đồ thị
Chương 4: Hệ thức lượng trong tam giác
Chương 5: Vectơ
Chương 6: Thống kê
Hoạt động thực hành và trải nghiệm - Tập 1
Chương 7: Bất phương trình bậc hai một ẩn
Chương 8: Đại số tổ hợp
Chương 9: Phương pháp toạ độ trong mặt phẳng
Chương 10: Xác suất
Hoạt động thực hành và trải nghiệm - Tập 2
Toán 10 - Kết nối tri thức
Chương 1: Mệnh đề và tập hợp
Chương 2: Bất phương trình và hệ bất phương trình bậc nhất hai ẩn
Chương 3: Hệ thức lượng trong tam giác
Chương 4: Vectơ
Chương 5: Các số đặc trưng của mẫu số liệu không ghép nhóm
Hoạt động thực hành trải nghiệm - Tập 1
Chương 6: Hàm số, đồ thị và ứng dụng
Chương 7: Phương pháp tọa độ trong mặt phẳng
Chương 8: Đại số tổ hợp
Chương 9: Tính xác suất theo định nghĩa cổ điển
Hoạt động thực hành trải nghiệm - Tập 2
Toán 10 - Cánh diều
Chương 1: Mệnh đề toán học. Tập hợp
Chương 2: Bất phương trình và hệ bất phương trình bậc nhất hai ẩn
Chương 3: Hàm số và đồ thị
Chương 4: Hệ thức lượng trong tam giác. Vectơ
Hoạt động thực hành và trải nghiệm -Tập 1
Chương 5: Đại số tổ hợp
Chương 6: Một số yếu tố thống kê và xác suất
Hoạt động thực hành và trải nghiệm - Tập 2
Chương 7: Phương pháp tọa độ trong mặt phẳng
Thực hành phần mềm Geogebra
Toán 11
Toán 11 - Chân trời sáng tạo
Chương 1: Hàm số lượng giác và phương trình lượng giác
Chương 2: Dãy số. Cấp số cộng. Cấp số nhân
Chương 3: Giới hạn. Hàm số liên tục
Chương 4: Đường thẳng và mặt phẳng. Quan hệ song song trong không gian
Chương 5: Các số đặc trưng đo xu thế trung tâm cho mẫu số liệu ghép nhóm
Hoạt động thực hành và trải nghiệm - Tập 1
Chương 6: Hàm số mũ và hàm số lôgarit
Chương 7: Đạo hàm
Chương 8: Quan hệ vuông góc trong không gian
Chương 9: Xác suất
Hoạt động thực hành trải nghiệm - Tập 2
Toán 11 - Kết nối tri thức
Chương 1: Hàm số lượng giác và phương trình lượng giác
Chương 2: Dãy số. Cấp số cộng và cấp số nhân
Chương 3: Các số đặc trưng đo xu thế trung tâm của mẫu số liệu ghép nhóm
Chương 4: Quan hệ song song trong không gian
Chương 5: Giới hạn. Hàm số liên tục
Hoạt động thực hành trải nghiệm - Tập 1
Hoạt động thực hành trải nghiệm - Tập 2
Chương 6: Hàm số mũ và hàm số lôgarit
Chương 7: Quan hệ vuông góc trong không gian
Chương 8: Các quy tắc tính xác suất
Chương 9: Đạo hàm
Toán 11 - Cánh diều
Chương 1: Hàm số lượng giác và phương trình lượng giác
Chương 2: Dãy số. Cấp số cộng. Cấp số nhân
Chương 3: Giới hạn. Hàm số liên tục
Hoạt động thực hành và trải nghiệm - Tập 1
Chương 4: Đường thẳng và mặt phẳng trong không gian. Quan hệ song song
Chương 5: Một số yếu tố thống kê và xác suất
Chương 6: Hàm số mũ và hàm số lôgarit
Chương 7: Đạo hàm
Chương 8: Quan hệ vuông góc trong không gian. Phép chiếu vuông góc
Hoạt động thực hành và trải nghiệm - Tập 2
Chuyên đề học tập Chân Trời Sáng Tạo
Chuyên đề học tập Kết Nối Tri Thức
Chuyên đề học tập Cánh diều
Toán 12
SGK Toán 12 - Chân trời sáng tạo
Chương 1. Ứng dụng đạo hàm để khảo sát hàm số
Chương 2. Vectơ và hệ tọa độ trong không gian
Chương 3. Các số đặc trưng đo mức độ phân tán cho mẫu số liệu ghép nhóm
Hoạt động thực hành và trải nghiệm
Chương 4. Nguyên hàm. Tích phân.
Chương 5. Phương trình mặt phẳng, đường thẳng, mặt cầu
Chương 6. Xác suất có điều kiện
Hoạt động thực hành và trải nghiệm
SGK Toán 12 - Kết nối tri thức
Chương 1. Ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số
Chương 2. Vectơ và hệ trục tọa độ trong không gian
Chương 3. Các số đặc trưng đo mức độ phân tán của mẫu số liệu ghép nhóm
Hoạt động thực hành và trải nghiệm
Chương 4. Nguyên hàm và Tích phân.
Chương 5. Phương pháp tọa độ trong không gian
Chương 6. Xác suất có điều kiện
Hoạt động thực hành và trải nghiệm
SGK Toán 12 - Cánh diều
Chương 1. Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số
Chương 2. Tọa độ của vectơ trong không gian
Chương 3. Các số đặc trưng đo mức độ phân tán cho mẫu số liệu ghép nhóm
Chương 4. Nguyên hàm. Tích phân
Chương 5. Phương trình mặt phẳng, đường thẳng, mặt cầu trong không gian
Chương 6. Một số yếu tố xác suất
SBT Toán 12 - Chân trời sáng tạo (SBT)
SBT Toán 12 - Kết nối tri thức (SBT)
Chương 1. Ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số
Chương 2. Vectơ và hệ trục tọa độ trong không gian
Chương 3. Các số đặc trưng đo mức độ phân tán của mẫu số liệu ghép nhóm
Chương 4. Nguyên hàm và Tích phân.
Chương 5. Phương pháp tọa độ trong không gian
Chương 6. Xác suất có điều kiện
Bài tập ôn tập cuối năm
Đề minh họa kiểm tra cuối học kì II
SBT Toán 12 - Cánh diều (SBT)
Chương 1. Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số
Chương 2. Tọa độ của vectơ trong không gian
Chương 3. Các số đặc trưng đo mức độ phân tán cho mẫu số liệu ghép nhóm
Chương 4. Nguyên hàm. Tích phân
Chương 5. Phương trình mặt phẳng, đường thẳng, mặt cầu trong không gian
Chương 6. Một số yếu tố xác suất
Công thức toán mới nhất
[Lớp 12] Khoảng cách từ một điểm đến một mặt phẳng
[Lớp 12] Diện tích hình phẳng giới hạn bởi đồ thị của các hàm số
[Lớp 12] Cách tìm toạ độ của một vectơ vuông góc với hai vectơ cho trước
[Lớp 12] Biểu thức toạ độ của tích vô hướng
Bài tập toán mới nhất
Luyện tập 6 trang 114 Toán 11 Tập 2
Một thùng đựng rác có dạng khối chóp cụt tứ giác đều với hai cạnh đáy lần lượt dài 2 dm và 3 dm, chiều cao bằng 4 dm. Tính thể tích của thùng đựng rác.
Luyện tập 5 trang 114 Toán 11 Tập 2
Cho khối tứ diện đều ABCD cạnh a. Chứng minh rằng thể tích của khối tứ diện đó bằng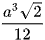 
.
Luyện tập 4 trang 112 Toán 11 Tập 2
Tính thể tích của khối lăng trụ ABC.A’B’C’ biết tất cả các cạnh bằng a và hình chiếu của A’ trên mặt phẳng (ABC) là trung điểm của AB.
Hoạt động 4 trang 112 Toán 11 Tập 2
Hãy nêu lại công thức tính thể tích của khối lăng trụ đứng tam giác, khối lăng trụ đứng tứ giác.
Luyện tập 3 trang 111 Toán 11 Tập 2
Cho hình chóp đều S.ABC. Gọi A’, B’, C’ lần lượt là trung điểm của các đoạn thẳng SA, SB, SC. Chứng minh rằng phần hình chóp đã cho giới hạn bởi hai mặt phẳng (ABC) và (A’B’C’) là hình chóp cụt đều.
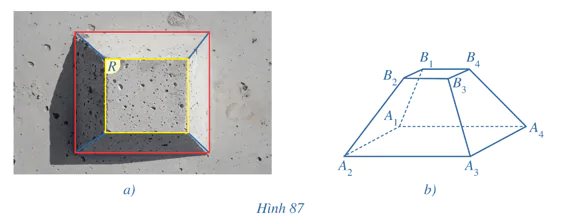
Hoạt động 3 trang 110 Toán 11 Tập 2
Khối bê tông ở Hình 87a gợi nên hình ảnh một hình chóp bị cắt đi bởi mặt phẳng (R) song song với đáy. Hình 87b là hình biểu diễn của khối bê tông ở Hình 87a. Hãy dự đoán về mối quan hệ giữa các đường thẳng chứa cạnh A1B1, A2B2, A3B3, A4B4.
Luyện tập 2 trang 110 Toán 11 Tập 2
Cho hình chóp tam giác đều S.ABC. Chứng minh rằng các cạnh bên tạo với mặt phẳng chứa đáy các góc bằng nhau.
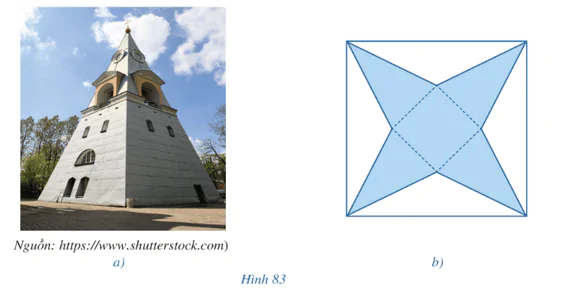
Hoạt động 2 trang 108 Toán 11 Tập 2
Để tạo mô hình một tháp chuông ở Hình 83a từ một tấm bìa hình vuông, bạn Dũng cắt bỏ phần màu trắng gồm bốn tam giác cân bằng nhau có đáy là các cạnh của tấm bìa (Hình 83b) rồi gấp lại phần màu xanh để tạo thành một hình chóp tứ giác. Quan sát Hình 83a, 83b và cho biết:
a) Đáy của hình chóp mà bạn Dũng tạo ra là tứ giác có tính chất gì;
b) Các cạnh bên của hình chóp đó có bằng nhau hay không.
Luyện tập 1 trang 108 Toán 11 Tập 2
Cho hình lập phương có cạnh bằng a. Tính độ dài đường chéo của hình lập phương đó.
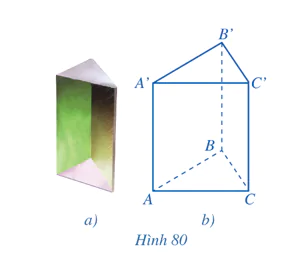
Hoạt động 1 trang 107 Toán 11 Tập 2
Cho hình lăng trụ tam giác có các mặt bên là hình chữ nhật ở Hình 80a, 80b. Hãy cho biết mỗi cạnh bên của hình lăng trụ đó có vuông góc với các mặt đáy hay không.
Câu hỏi khởi động trang 107 Toán 11 Tập 2
Ở lớp 7, ta đã làm quen với hình lăng trụ đứng tam giác và hình lăng trụ đứng tứ giác, tức là những hình lăng trụ đứng có đáy là tam giác hoặc tứ giác.
Hình lăng trụ đứng với đáy là đa giác, đặc biệt là đa giác đều, có tính chất gì (Hình 97)?
Luyện tập 5 trang 106 Toán 11 Tập 2
Cho hình chóp tam giác S.ABC có đáy ABC là tam giác đều cạnh a, SA ⊥ (ABC). Tính d(SA, BC).
Hoạt động 5 trang 104 Toán 11 Tập 2
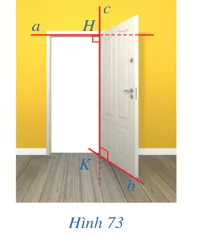
Trong Hình 73, khuôn cửa phía trên và mép cánh cửa phía dưới gợi nên hình ảnh hai đường thẳng a và b chéo nhau, hai bản lề của cánh cửa nằm trên đường thẳng c.
Quan sát Hình 73 và cho biết đường thẳng c có vừa cắt, vừa vuông góc với cả hai đường thẳng a và b hay không.
Luyện tập 4 trang 104 Toán 11 Tập 2
Cho hình lăng trụ ABC.A’B’C’ có cạnh bên bằng a, góc giữa đường thẳng AA’ và mặt phẳng (ABC) bằng 60°. Tính khoảng cách giữa hai mặt phẳng (ABC) và (A’B’C’).
Hoạt động 4 trang 103 Toán 11 Tập 2
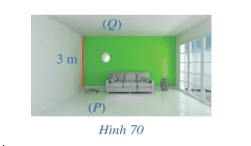
a) Trong Hình 70, sàn nhà và trần nhà của căn phòng gợi nên hình ảnh hai mặt phẳng song song (P), (Q). Chiều cao của căn phòng là 3 m.
Chiều cao đó gợi nên khái niệm gì trong hình học liên quan đến hai mặt phẳng song song (P), (Q)?
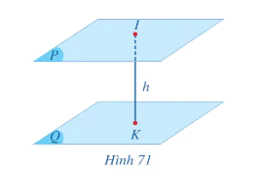
b) Cho hai mặt phẳng (P) và (Q) song song với nhau. Xét điểm I tuỳ ý trong mặt phẳng (P), lấy K là hình chiếu của I trên (Q) (Hình 71). Khoảng cách IK từ điểm I đến mặt phẳng (Q) có phụ thuộc vào vị trí của điểm I trong mặt phẳng (P) hay không? Vì sao?
Luyện tập 3 trang 103 Toán 11 Tập 2
Cho hình chóp S.ABC có SA = a, góc giữa SA và mp(ABC) là 60°. Gọi M, N lần lượt là trung điểm của cạnh SA và SB. Chứng minh MN // (ABC) và tính d(MN, (ABC)).
Hoạt động 3 trang 102 Toán 11 Tập 2
Trong Hình 67, thanh gỗ dọc phía trên các cột và mặt đường hành lang gợi nên hình ảnh đường thẳng Δ và mặt phẳng (P) song song với nhau, chiều cao của chiếc cột có đỉnh cột A là khoảng cách từ điểm A đến mặt phẳng (P).
a) Khoảng cách từ điểm A đến mặt phẳng (P) có phụ thuộc vào vị trí của điểm A trên đường thẳng Δ hay không? Vì sao?
b) Khoảng cách đó gợi nên khái niệm nào trong hình học liên quan đến đường thẳng Δ và mặt phẳng (P)?
Luyện tập 2 trang 102 Toán 11 Tập 2
Người ta dựng các cột đèn vuông góc với mặt đường, trong đó mỗi cột đèn gợi nên hình ảnh một đường thẳng. Khoảng cách giữa hai chân cột đèn liên tiếp đo được là 5 m. Tại sao có thể nói khoảng cách giữa hai cột đèn đó là 5 m?
Hoạt động 2 trang 102 Toán 11 Tập 2
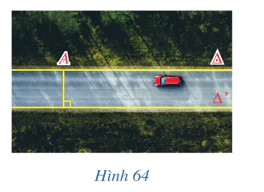
Trong Hình 64, hai mép của con đường gợi nên hình ảnh hai đường thẳng song song Δ và ∆’. Xét điểm A trên đường thẳng Δ.
a) Khoảng cách từ điểm A đến đường thẳng Δ’ có phụ thuộc vào vị trí của điểm A trên đường thẳng Δ hay không? Vì sao?
b) Khoảng cách đó gợi nên khái niệm gì trong hình học liên quan đến hai đường thẳng song song Δ và Δ’?
Luyện tập 1 trang 101 Toán 11 Tập 2
Cho hình chóp S.ABC có SA ⊥ (ABC), AI ⊥ BC (I ∈ BC), AH ⊥ SI (H ∈ SI). Chứng minh rằng khoảng cách từ A đến mặt phẳng (SBC) bằng AH.
Hoạt động 1 trang 101 Toán 11 Tập 2
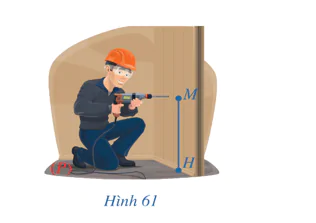
Khi lắp thiết bị cho nhà bạn Nam, bác thợ khoan tường tại vị trí M trên tường có độ cao so với nền nhà là MH = 80 cm. Quan sát Hình 61, nền nhà gợi nên mặt phẳng (P), cho biết độ dài đoạn thẳng MH gợi nên khái niệm gì trong hình học liên quan đến điểm M và mặt phẳng (P).
Câu hỏi khởi động trang 100 Toán 11 Tập 2
Hình 58 mô tả cách đo chiều cao của một người khi kiểm tra sức khỏe. Coi mặt bản sắt người đó đứng lên là mặt phẳng (P), mặt bản sắt áp vào đầu người đó là mặt phẳng (Q) song song với (P).
Luyện tập 4 trang 99 Toán 11 Tập 2
Cho hình chóp S.ABC có SA ⊥ SB, SB ⊥ SC, SC ⊥ SA. Chứng minh rằng:
a) (SAB) ⊥ (SBC);
b) (SBC) ⊥ (SCA);
c) (SCA) ⊥ (SAB).
Hoạt động 4 trang 98 Toán 11 Tập 2
Trong Hình 54, hai bìa của cuốn sách gợi nên hình ảnh hai mặt phẳng vuông góc với mặt bàn. Hãy dự đoán xem gáy sách có vuông góc với mặt bàn hay không.
Tài liệu toán mới nhất
[Toán 12-HK2] Bộ đề ôn thi cuối học kì 2 Toán 12 chuẩn cấu trúc mới năm 2024 – 2025
[Toán 12-HK2] Đề ôn thi HK2 Toán 12 năm 2024 – 2025 trường Quốc tế Á Châu – TP HCM
[Toán 12-HK2] 05 đề thi thử cuối học kì 2 môn Toán 12 năm học 2024 – 2025 có đáp án
[Toán 12-HK2] Đề ôn tập CK2 Toán 12 năm 2024 – 2025 trường THPT Hùng Vương – Bình Phước
[Toán 12-HK2] Bộ đề kiểm tra cuối học kỳ 2 môn Toán 12 năm học 2024 – 2025
[Toán 12-HK2] Bộ đề ôn tập kiểm tra cuối học kì 2 môn Toán 12 theo cấu trúc mới
[Toán 12-HK2] Đề kiểm tra cuối kì 2 Toán 12 năm 2023 – 2024 sở GD&ĐT Vĩnh Long
[Toán 12-HK2] Đề cuối học kỳ 2 Toán 12 năm 2023 – 2024 trường THPT Thị xã Quảng Trị
[Toán 12-HK2] Đề cuối kì 2 Toán 12 năm 2023 – 2024 trường THPT Lê Hồng Phong – Đắk Lắk
[Toán 12-HK2] Đề cuối học kì 2 Toán 12 năm 2023 – 2024 trường THPT Lê Hồng Phong – Quảng Nam
[Toán 12-HK2] Đề kiểm tra học kỳ 2 Toán 12 năm 2023 – 2024 sở GD&ĐT Bình Dương
[Toán 12-HK2] Đề cuối học kỳ 2 Toán 12 năm 2023 – 2024 trường THPT Nguyễn Huệ – Quảng Nam
[Toán 12-HK2] Đề kiểm tra cuối học kì 2 Toán 12 năm 2023 – 2024 sở GD&ĐT Bắc Ninh
[Toán 12-HK2] Đề cuối kỳ 2 Toán 12 năm 2023 – 2024 trường THPT Quế Sơn – Quảng Nam
[Toán 12-HK2] Đề cuối học kì 2 Toán 12 năm 2023 – 2024 trường THPT Chế Lan Viên – Quảng Trị
[Toán 12-HK2] Đề học kì 2 Toán 12 năm 2023 – 2024 trường THPT Kẻ Sặt – Hải Dương
[Toán 12-HK2] Đề cuối học kỳ 2 Toán 12 năm 2023 – 2024 trường THPT Bình Giang – Hải Dương
[Toán 12-HK2] Đề cuối học kì 2 Toán 12 năm 2023 – 2024 trường THPT Ngô Quyền – Thái Nguyên
[Toán 12-HK2] Đề cuối học kỳ 2 Toán 12 năm 2023 – 2024 trường THPT Lê Lợi – Quảng Trị
[Toán 12-HK2] Đề cuối học kỳ 2 Toán 12 năm 2023 – 2024 trường Lạc Hồng – TP HCM
[Toán 12-HK2] Đề thi học kỳ 2 Toán 12 năm 2023 – 2024 trường THPT Nguyễn Trãi – Thái Bình
[Toán 12-HK2] Đề cuối học kỳ 2 Toán 12 năm 2023 – 2024 trường THPT Lạc Long Quân – Khánh Hòa
[Toán 12-HK2] Đề kiểm tra HK2 Toán 12 năm 2023 – 2024 trường THPT Phan Ngọc Hiển – Cà Mau
[Toán 12-HK2] Đề học kì 2 Toán 12 năm 2023 – 2024 trường THPT Nguyễn Quốc Trinh – Hà Nội
Công thức mới cập nhật
[Lớp 12] Công thức Bayes
Công thức Bayes
[Lớp 12] Công thức xác suất toàn phần
Công thức xác suất toàn phần
[Lớp 12] Góc giữa hai mặt phẳng
Góc giữa hai mặt phẳng
[Lớp 12] Góc giữa đường thẳng và mặt phẳng
Góc giữa đường thẳng và mặt phẳng
[Lớp 12] Góc giữa hai đường thẳng
Góc giữa hai đường thẳng
[Lớp 12] Khoảng cách từ một điểm đến một mặt phẳng
Khoảng cách từ một điểm đến một mặt phẳng
[Lớp 12] Thể tích của khối tròn xoay
Thể tích của khối tròn xoay
[Lớp 12] Tính thể tích của vật thể
Tính thể tích của vật thể
[Lớp 12] Diện tích hình phẳng giới hạn bởi đồ thị của các hàm số
Diện tích hình phẳng giới hạn bởi đồ thị của các hàm số y = f(x), y = g(x) và hai đường thẳng x = a, x = b
[Lớp 12] Tính diện tích hình phẳng
Tính diện tích hình phẳng
Tài liệu mới cập nhật
[Toán 12-HK2] Bộ đề ôn thi cuối học kì 2 Toán 12 chuẩn cấu trúc mới năm 2024 – 2025
Tài liệu gồm 79 trang, được biên soạn bởi thầy giáo Nguyễn Hữu Chung Kiên, tuyển tập 20 đề ôn thi cuối học kì 2 môn Toán 12 chuẩn cấu trúc mới năm học 2024 – 2025.
[Toán 12-HK2] Đề ôn thi HK2 Toán 12 năm 2024 – 2025 trường Quốc tế Á Châu – TP HCM
Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 12 đề ôn thi cuối học kì 2 môn Toán 12 năm học 2024 – 2025 trường Quốc tế Á Châu, thành phố Hồ Chí Minh.
[Toán 12-HK2] 05 đề thi thử cuối học kì 2 môn Toán 12 năm học 2024 – 2025 có đáp án
Tài liệu gồm 25 trang, được biên soạn bởi thầy giáo Chu Hoàng Minh, tuyển tập 05 đề thi thử cuối học kì 2 môn Toán 12 năm học 2024 – 2025 có đáp án.
[Toán 12-HK2] Đề ôn tập CK2 Toán 12 năm 2024 – 2025 trường THPT Hùng Vương – Bình Phước
Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 12 bộ đề ôn tập kiểm tra cuối học kì 2 môn Toán 12 năm học 2024 – 2025 trường THPT Hùng Vương, tỉnh Bình Phước.
[Toán 12-HK2] Bộ đề kiểm tra cuối học kỳ 2 môn Toán 12 năm học 2024 – 2025
Tài liệu gồm 43 trang, được biên soạn bởi tác giả Toán Từ Tâm, tuyển tập bộ đề ôn tập kiểm tra cuối học kỳ 2 môn Toán 12 năm học 2024 – 2025.
[Toán 12-HK2] Bộ đề ôn tập kiểm tra cuối học kì 2 môn Toán 12 theo cấu trúc mới
Tài liệu gồm 95 trang, được biên soạn bởi thầy giáo Phạm Lê Duy, tuyển tập bộ đề ôn tập kiểm tra cuối học kì 2 môn Toán 12 theo cấu trúc mới.
[Toán 12-HK2] Đề kiểm tra cuối kì 2 Toán 12 năm 2023 – 2024 sở GD&ĐT Vĩnh Long
Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 12 đề kiểm tra cuối học kì 2 môn Toán 12 năm học 2023 – 2024 sở Giáo dục và Đào tạo tỉnh Vĩnh Long; đề thi có đáp án trắc nghiệm mã đề 101 – 102 – 103 – 104.
[Toán 12-HK2] Đề cuối học kỳ 2 Toán 12 năm 2023 – 2024 trường THPT Thị xã Quảng Trị
Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 12 đề kiểm tra cuối học kỳ 2 môn Toán 12 năm học 2023 – 2024 trường THPT Thị xã Quảng Trị, tỉnh Quảng Trị; đề thi có đáp án trắc nghiệm mã đề 125 – 126.
[Toán 12-HK2] Đề cuối kì 2 Toán 12 năm 2023 – 2024 trường THPT Lê Hồng Phong – Đắk Lắk
Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 12 đề kiểm tra đánh giá cuối học kì 2 môn Toán 12 năm học 2023 – 2024 trường THPT Lê Hồng Phong, tỉnh Đắk Lắk; đề thi có đáp án và hướng dẫn chấm điểm.
[Toán 12-HK2] Đề cuối học kì 2 Toán 12 năm 2023 – 2024 trường THPT Lê Hồng Phong – Quảng Nam
Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 12 đề kiểm tra cuối học kì 2 môn Toán 12 năm học 2023 – 2024 trường THPT Lê Hồng Phong, tỉnh Quảng Nam.