Giải bài tập Toán 12 Chương 1. Ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số | Kết Nối Tri Thức
Hướng dẫn giải chi tiết SBT Chương 1. Ứng dụng đạo hàm để khảo sát hàm số. Đạo hàm, bảng biến thiên, đồng biến nghịch biến, cực trị, min, max, tiệm cận đứng, tiệm cận ngang, tiệm cận xiên
Giải bài tập Bài 1. Tính đơn điệu và cực trị của hàm số.

Bài 1.1 trang 8 SBT Toán 12 Tập 1
Cho hàm f(x) xác định trên ℝ và đạo hàm f'(x) có đồ thị như hình bên. Sử dụng đồ thị hàm số y = f'(x), hãy cho biết: a) Các khoảng đồng biến, khoảng nghịch biến của hàm số f(x); b) Hàm số f(x) có cực đại, cực tiểu không?

Bài 1.2 trang 9 SBT Toán 12 Tập 1
Tìm các khoảng đồng biến, khoảng nghịch biến và cực trị (nếu có) của các hàm số sau.

Bài 1.3 trang 9 SBT Toán 12 Tập 1
Xét tính đơn điệu và tìm các cực trị (nếu có) của các hàm số sau.

Bài 1.4 trang 9 SBT Toán 12 Tập 1
Tìm các khoảng đơn điệu và các cực trị (nếu có) của các hàm số sau.

Bài 1.5 trang 9 SBT Toán 12 Tập 1
Tìm các giá trị của tham số m sao cho hàm số y đồng biến trên ℝ.
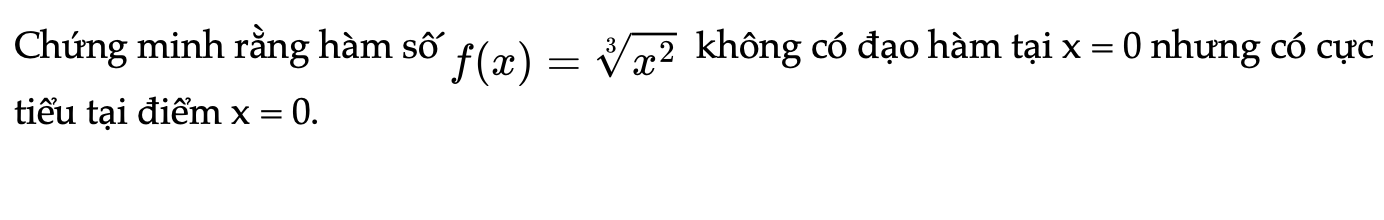
Bài 1.6 trang 9 SBT Toán 12 Tập 1
Chứng minh rằng hàm số f(x) không có đạo hàm tại x = 0 nhưng có cực tiểu tại điểm x = 0.

Bài 1.7 trang 9 SBT Toán 12 Tập 1
Một nhà phân phối đồ chơi trẻ em xác định hàm chi phí C(x) và hàm doanh thu R(x) (đều tính bằng trăm nghìn đồng) cho một loại đồ chơi như sau.

Bài 1.8 trang 9 SBT Toán 12 Tập
Hàm chi phí và hàm doanh thu (đều tính bằng triệu đồng) của một loại sản phẩm lần lượt là C(x) = 25,5x + 1 000 và R(x) = 75,5x, trong đó x là số đơn vị sản phẩm đó được sản xuất và bán ra.

Bài 1.9 trang 10 SBT Toán 12 Tập 1
Một con lắc lò xo, gồm một vật nặng có khối lượng 1 kg được gắn vào một lò xo được cố định một đầu, dao động điều hòa với biên độ A = 0,24 m và chu kì T = 4 giây.

Bài 1.10 trang 10 SBT Toán 12 Tập 1
Một vật chuyển động dọc theo trục số nằm ngang, chiều dương từ trái sang phải. Giả sử vị trí của vật x (mét) từ thời điểm t = 0 giây đến thời điểm t = 5 giây được cho bởi công thức x(t).
Giải bài tập Bài 2. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số.
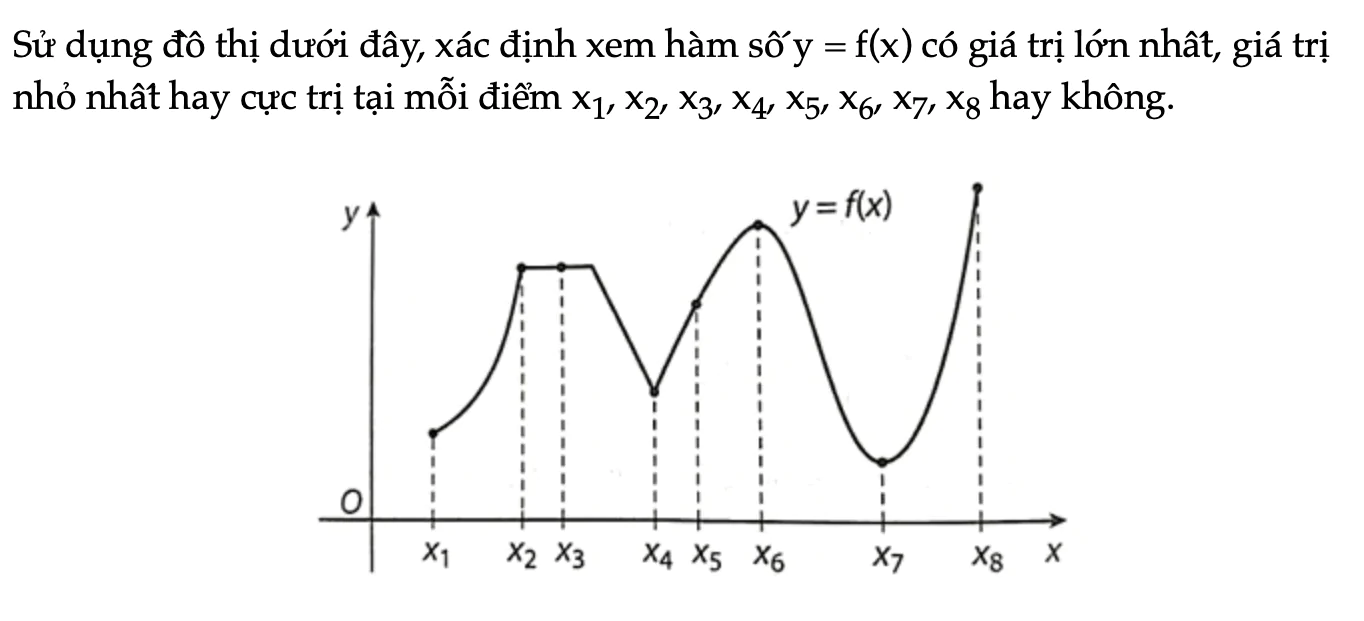
Bài 1.11 trang 14 SBT Toán 12 Tập 1
Sử dụng đồ thị dưới đây, xác định xem hàm số y = f(x) có giá trị lớn nhất, giá trị nhỏ nhất hay cực trị tại mỗi điểm x1, x2, x3, x4, x5, x6, x7, x8 hay không.

Bài 1.12 trang 14 SBT Toán 12 Tập 1
Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của các hàm số sau.

Bài 1.13 trang 14 SBT Toán 12 Tập 1
Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của các hàm số sau.
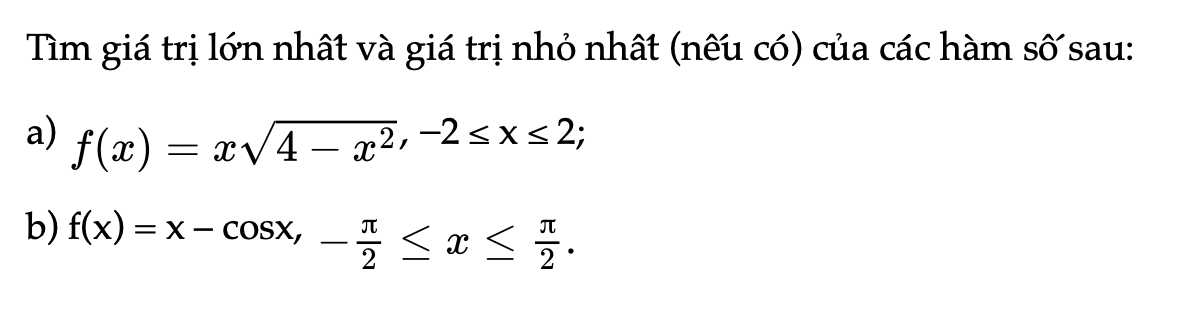
Bài 1.14 trang 14 SBT Toán 12 Tập 1
Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của các hàm số sau.
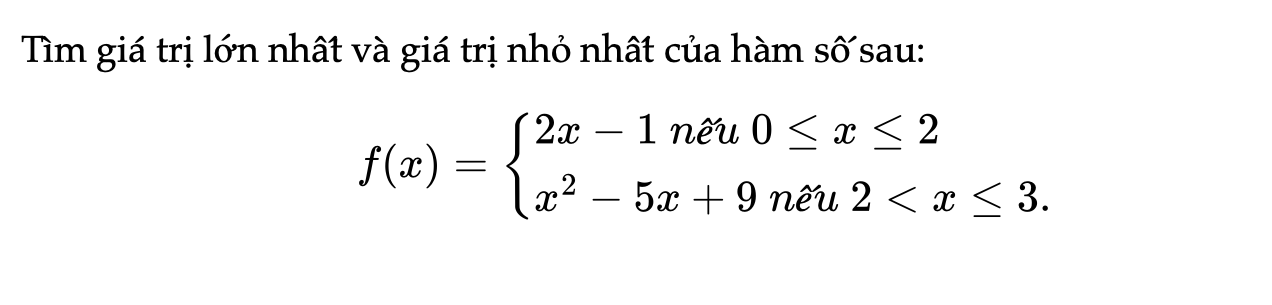
Bài 1.15 trang 15 SBT Toán 12 Tập 1
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số sau.

Bài 1.16 trang 15 SBT Toán 12 Tập 1
Lợi nhuận thu được P của một công ty khi dùng số tiền s chi cho quảng cáo được cho bởi công thức.

Bài 1.17 trang 15 SBT Toán 12 Tập 1
Giải bài toán bằng cách tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số.

Bài 1.18 trang 15 SBT Toán 12 Tập 1
Hai nguồn nhiệt đặt cách nhau s mét, một nguồn có cường độ a đặt ở điểm A và một nguồn có cường độ b đặt ở điểm B. Cường độ nhiệt tại điểm P nằm trên đoạn thẳng nối A và B được tính theo công thức sau. Tại điểm nào nằm giữa A và B nhiệt độ sẽ thấp nhất?

Bài 1.19 trang 16 SBT Toán 12 Tập 1
Một vật được phóng lên trời theo một góc xiên θ (45° ≤ x ≤ 90°) so với phương ngang với vận tốc ban đầu v0 (feet/giây) tính từ chân mặt phẳng nghiêng tạo một góc 45° so với phương ngang (xem hình vẽ).

Bài 1.20 trang 16 SBT Toán 12 Tập 1
Một chiếc xe nhỏ chuyển động không có ma sát, gắn vào tường bằng một lò xo (xem hình vẽ), được kéo ra khỏi vị trí đứng yên 10 cm rồi thả ra tại thời điểm ban đầu t = 0 giây để chuyển động trong 4 giây. Vị trí s (cm) tại thời điểm t giây là s = 10cosπt.
Giải bài tập Bài 3. Đường tiệm cận của đồ thị hàm số.
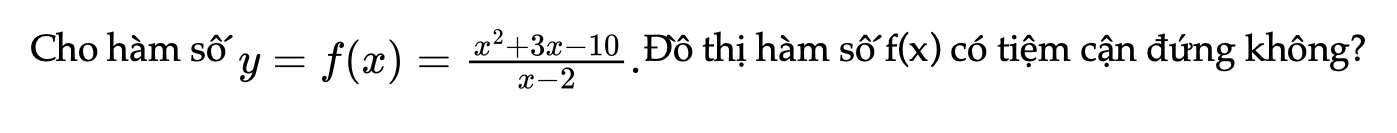
Bài 1.21 trang 19 SBT Toán 12 Tập 1
Cho hàm số y=f(x). Đồ thị hàm số f(x) có tiệm cận đứng không?

Bài 1.22 trang 19 SBT Toán 12 Tập 1
Tìm các đường tiệm cận của đồ thị các hàm số sau.

Bài 1.23 trang 19 SBT Toán 12 Tập 1
Tìm tiệm cận đứng và tiệm cận xiên của đồ thị hàm số sau.
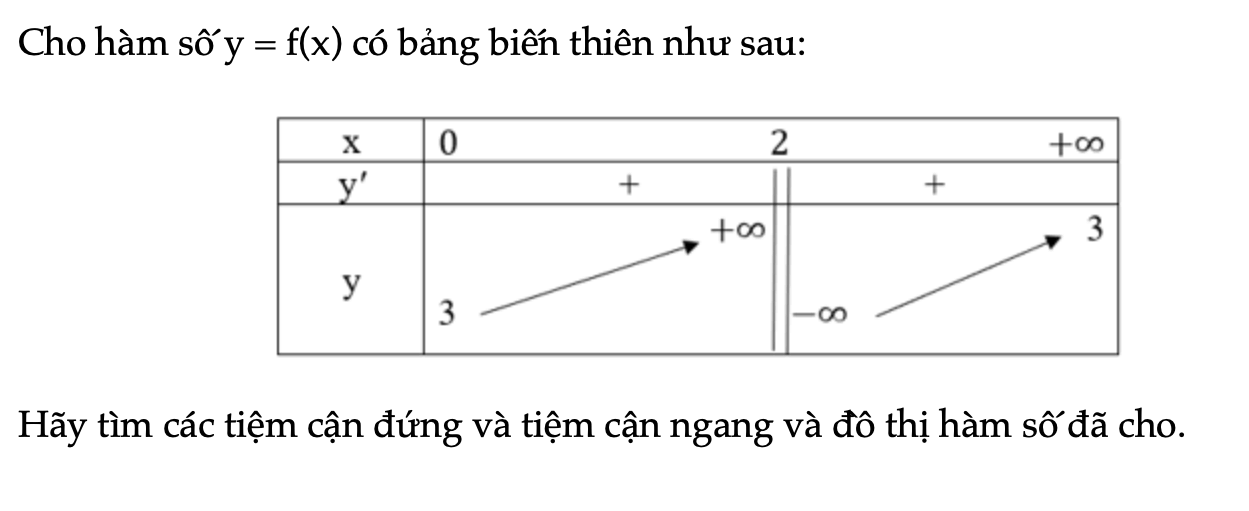
Bài 1.24 trang 19 SBT Toán 12 Tập 1
Cho hàm số y = f(x) có bảng biến thiên như sau. Hãy tìm các tiệm cận đứng và tiệm cận ngang và đồ thị hàm số đã cho.
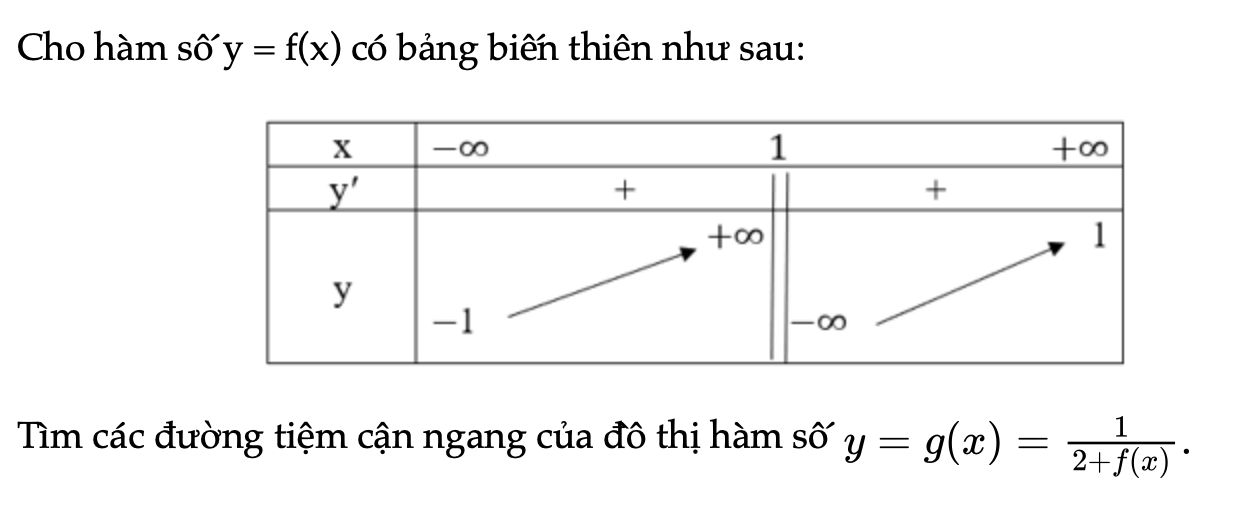
Bài 1.25 trang 19 SBT Toán 12 Tập 1
Cho hàm số y = f(x) có bảng biến thiên như sau. Tìm các đường tiệm cận ngang của đồ thị hàm số.

Bài 1.26 trang 20 SBT Toán 12 Tập 1
Cho hàm số y có đồ thị (C). Tính tích khoảng cách từ một điểm tùy ý thuộc (C) đến hai đường tiệm cận của nó.
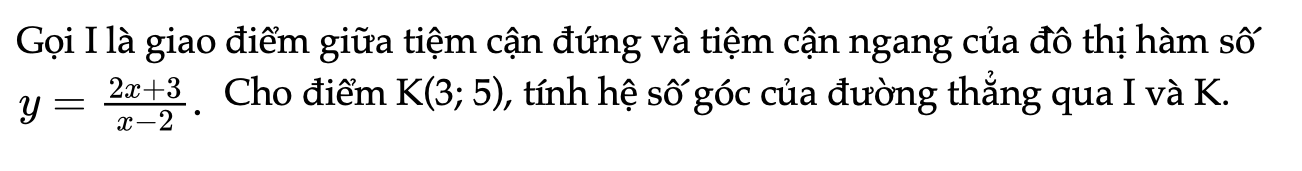
Bài 1.27 trang 20 SBT Toán 12 Tập 1
Gọi I là giao điểm giữa tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y. Cho điểm K(3; 5), tính hệ số góc của đường thẳng qua I và K.
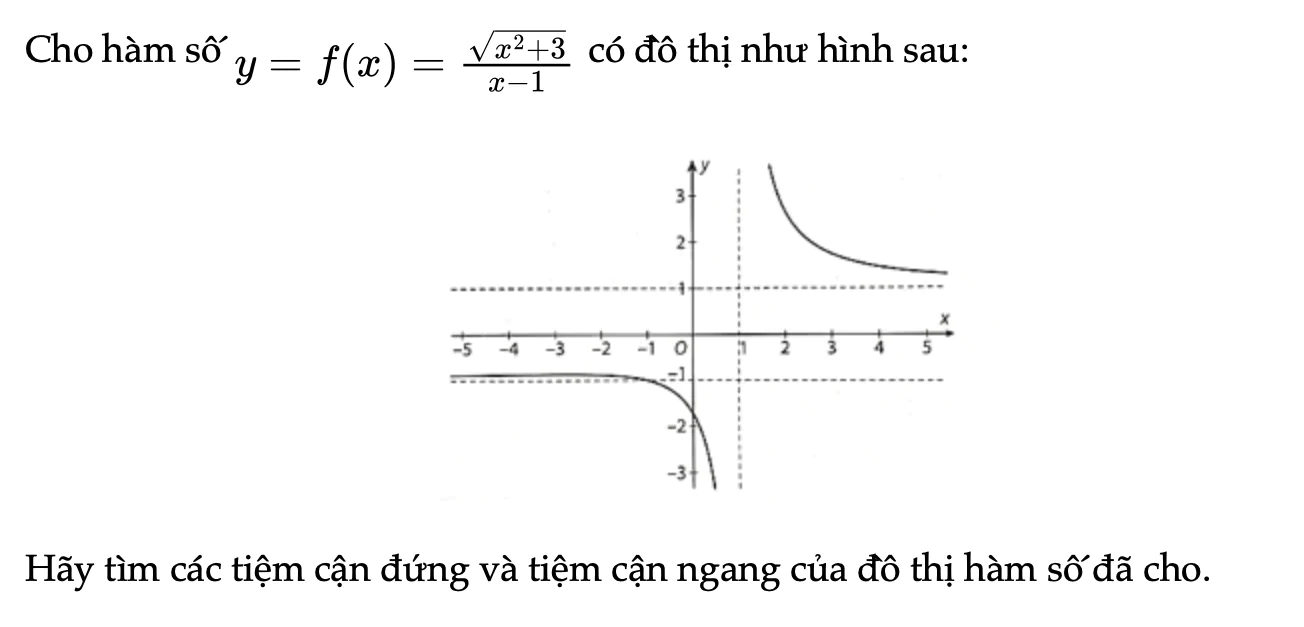
Bài 1.28 trang 20 SBT Toán 12 Tập 1
Hãy tìm các tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho.

Bài 1.29 trang 20 SBT Toán 12 Tập 1
Cho hàm số y = f(x) có đồ thị (C). Gọi tổng khoảng cách từ một điểm (x; y) ∈ (C), với x > 3, tới hai đường tiệm cận của (C) là g(x). Tìm các đường tiệm cận của đồ thị hàm số y = g(x).

Bài 1.30 trang 20 SBT Toán 12 Tập
Một bình chứa 200 ml dung dịch muối với nồng độ 5 mg/ml. a) Tính nồng độ dung dịch muối trong bình sau khi thêm vào x ml dung dịch muối với nồng độ 10 mg/ml. b) Phải thêm bao nhiêu mililít vào bình để có dung dịch muối với nồng độ 9 mg/ml?
Giải bài tập Bài 4. Khảo sát sự biến thiên và vẽ đồ thị của hàm số.

Bài 1.31 trang 25 SBT Toán 12 Tập 1
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau.

Bài 1.32 trang 25 SBT Toán 12 Tập 1
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau.

Bài 1.33 trang 25 SBT Toán 12 Tập 1
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau.

Bài 1.34 trang 25 SBT Toán 12 Tập 1
Cho hàm số y = f(x) có đạo hàm f'(x) xác định trên ℝ và f'(x) có đồ thị như hình vẽ sau. Tìm các khoảng đồng biến, khoảng nghịch biến và các điểm cực trị của hàm số y = f(x).
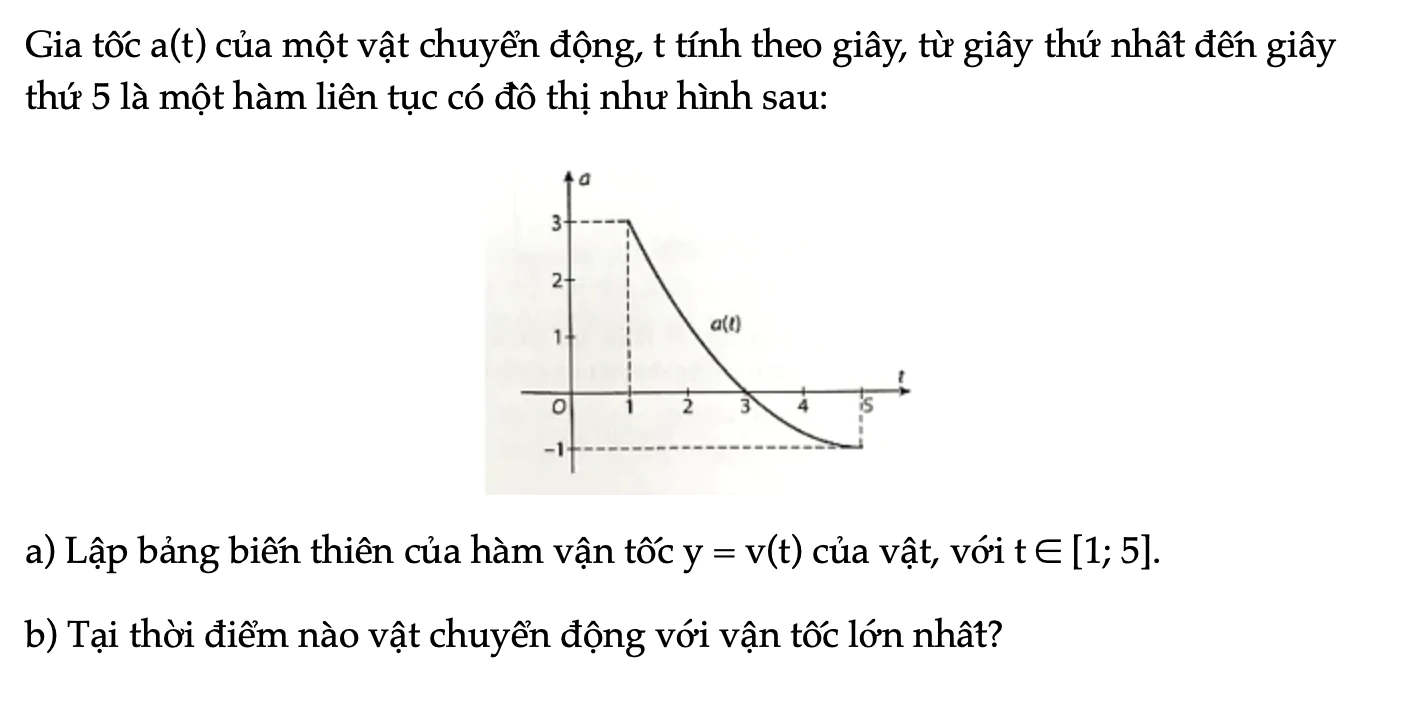
Bài 1.35 trang 25 SBT Toán 12 Tập 1
Gia tốc a(t) của một vật chuyển động, t tính theo giây, từ giây thứ nhất đến giây thứ 5 là một hàm liên tục có đồ thị như hình sau. a) Lập bảng biến thiên của hàm vận tốc y = v(t) của vật. b) Tại thời điểm nào vật chuyển động với vận tốc lớn nhất.

Bài 1.36 trang 26 SBT Toán 12 Tập 1
Một mẫu giấy in hình chữ nhật được thiết kế với vùng in có diện tích 300 cm2, lề trái và lề phải là 2 cm, lề trên và lề dưới là 3 cm. Gọi x (cm) là chiều rộng của tờ giấy.

Bài 1.37 trang 26 SBT Toán 12 Tập 1
Giả sử chi phí để sản xuất x sản phẩm của một nhà máy được cho bởi C(x) = 0,2x2 + 10x + 5(triệu đồng). Khi đó, chi phí trung bình để sản xuất một đơn vị sản phẩm là f(x).
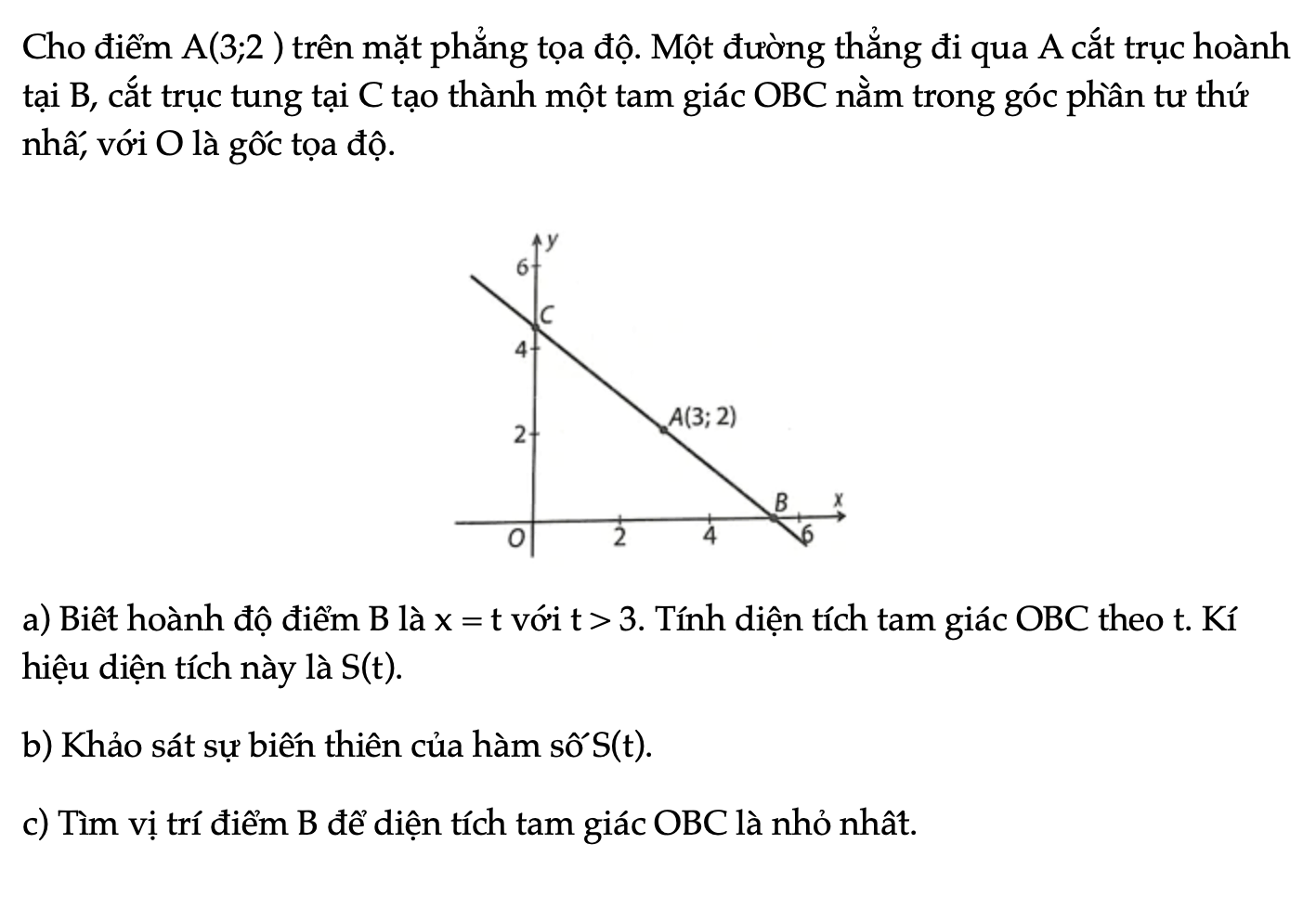
Bài 1.38 trang 26 SBT Toán 12 Tập 1
Cho điểm A(3;2 ) trên mặt phẳng tọa độ. Một đường thẳng đi qua A cắt trục hoành tại B, cắt trục tung tại C tạo thành một tam giác OBC nằm trong góc phần tư thứ nhấ, với O là gốc tọa độ.

Bài 1.39 trang 26 SBT Toán 12 Tập 1
Một quần thể cá được nuôi trong một hồ nhân tạo lúc ban đầu có 80 000 con. Sau t năm, số lượng quần thể cá nói trên được xác định bởi N(t). a) Khảo sát sự biến thiên của hàm số y = N(t). b) Số lượng tối đa có thể có của quần thể cá là bao nhiêu?
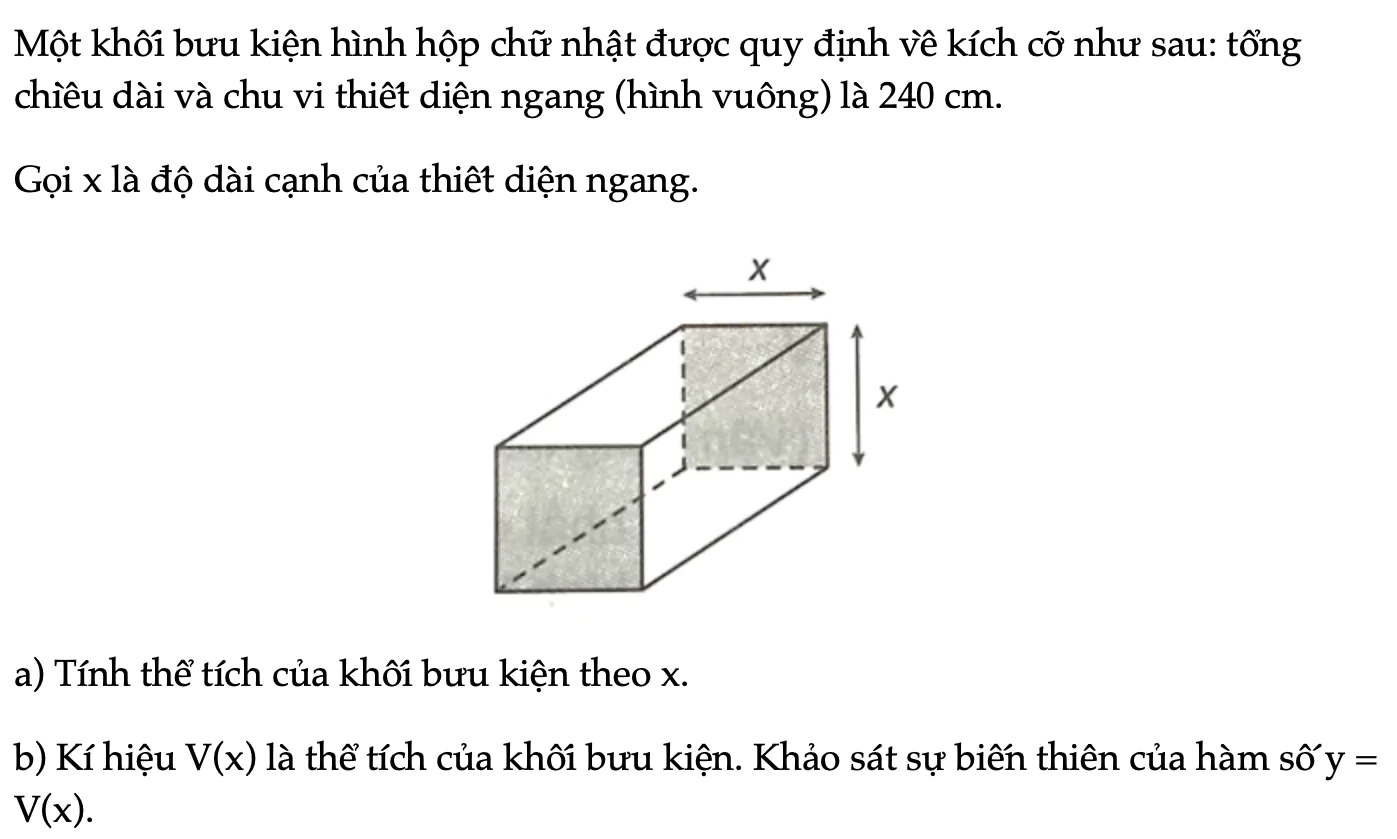
Bài 1.40 trang 27 SBT Toán 12 Tập 1
Một khối bưu kiện hình hộp chữ nhật được quy định về kích cỡ như sau: tổng chiều dài và chu vi thiết diện ngang (hình vuông) là 240 cm. a) Tính thể tích của khối bưu kiện theo x. b) Khảo sát sự biến thiên của hàm số V(x).
Giải bài tập Bài 5. Ứng dụng đạo hàm để giải quyết một số vấn đề liên quan đến thực tiễn.

Bài 1.41 trang 31 SBT Toán 12 Tập 1
Bác Hưng có một hàng rào thép dài 240 m và muốn rào cánh đồng thành một thửa ruộng hình chữ nhật giáp một con sông thẳng. Bác không cần rào phía cạnh con sông. Hỏi thửa ruộng có diện tích lớn nhất là bao nhiêu?

Bài 1.42 trang 31 SBT Toán 12 Tập 1
Doanh số bán hệ thống âm thanh nổi mới trong một khoảng thời gian dự kiến sẽ tuân theo đường cong logistic R = R(x), x ≥ 0, trong đó thời gian x được tính bằng năm. Hỏi tốc độ bán hàng đạt tối đa vào năm nào?

Bài 1.43 trang 31 SBT Toán 12 Tập 1
Một chiếc hộp dạng hình hộp chữ nhật có đáy là hình vuông và có thể tích là 2 000 cm3. Các kích thước của chiếc hộp là bao nhiêu nếu muốn lượng vật liệu dùng để sản xuất chiếc hộp là nhỏ nhất?

Bài 1.44 trang 31 SBT Toán 12 Tập 1
Một hòn đảo nhỏ cách điểm P trên bờ biển khoảng 3km, một thị trấn ở điểm A cách điểm P12 km. Nếu một người trên đảo chèo thuyền với vận tốc 2,5km/h và đi bộ với vận tốc 4km/h thì thuyền nên neo đậu ở vị trí nào để người đó đến thị trấn trong t ngắn nhất?

Bài 1.45 trang 32 SBT Toán 12 Tập 1
Chứng tỏ rằng một thùng hình trụ có thể tích V cố định cần ít vật liệu sản xuất nhất (tức là có diện tích về mặt nhỏ nhất) khi chiều cao của thùng gấp đôi bán kính đáy.

Bài 1.46 trang 32 SBT Toán 12 Tập 1
Ở 0℃, sự mất nhiệt H (tính bằng Lcal/m2h, ở đây Kcal là kilocalories và 1 Kcal = 1 000 calo) từ cơ thể của một người có thể được mô hình hóa bằng công thức H.

Bài 1.47 trang 32 SBT Toán 12 Tập 1
Doanh thu R (USD) từ việc cho thuê x căn hộ có thể được mô hình hóa bằng hàm số R.

Bài 1.48 trang 32 SBT Toán 12 Tập 1
Một công ty ước tính rằng chi phí C (USD) để sản xuất x đơn vị sản phẩm có thể được mô hình hóa bằng công thức.

Bài 1.49 trang 32 SBT Toán 12 Tập 1
a) Nếu C(x) (USD) là chi phí sản xuất x đơn vị hàng hóa, thì chi phí trung bình cho mỗi đơn vị là C(x). Chứng minh rằng nếu chi phí trung bình là nhỏ nhất thì chi phí biên bằng chi phí trung bình.

Bài 1.50 trang 33 SBT Toán 12 Tập 1
a) Chứng tỏ rằng nếu lợi nhuận P(x) là cực đại thì doanh thu biên bằng chi phí biên. b) Cho C(x) = 16 000 + 500x – 1,6x^2 + 0,004x^3 là hàm chi phí và p(x) = 1 700 – 7x là hàm cầu. Hãy tìm mức sản xuất sẽ tối đa hóa lợi nhuận.
Giải bài tập Bài tập cuối chương 1

Bài 1.51 trang 33 SBT Toán 12 Tập 1
Cho hàm số y = f(x) có đạo hàm trên (a;b). Xét các mệnh đề sau. Trong các mệnh để trên, mệnh đề nào đúng, mệnh đề nào sai?

Bài 1.52 trang 33 SBT Toán 12 Tập 1
Hàm số nào dưới đây nghịch biến trên tập xác định của nó?

Bài 1.53 trang 33 SBT Toán 12 Tập 1
Có tất cả bao nhiêu giá trị nguyên dương của tham số m để hàm số sau đồng biến trên từng khoảng xác định của nó?
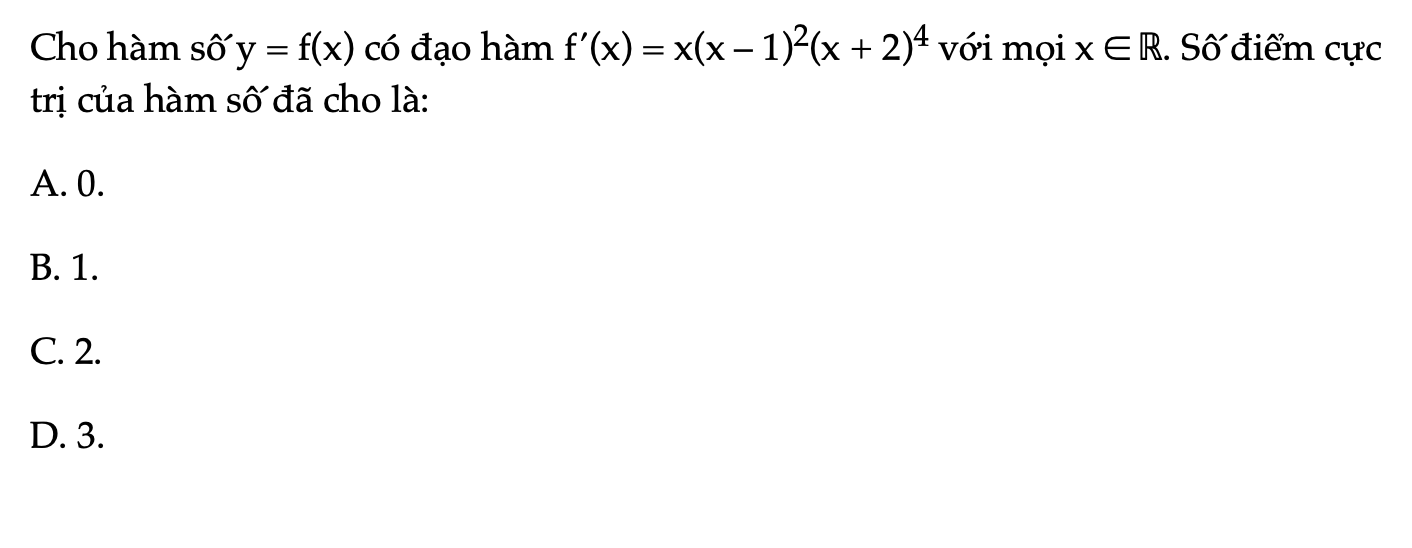
Bài 1.54 trang 34 SBT Toán 12 Tập 1
Cho hàm số y = f(x) có đạo hàm f'(x) = x(x – 1)2(x + 2)4 với mọi x ∈ ℝ. Số điểm cực trị của hàm số đã cho là?
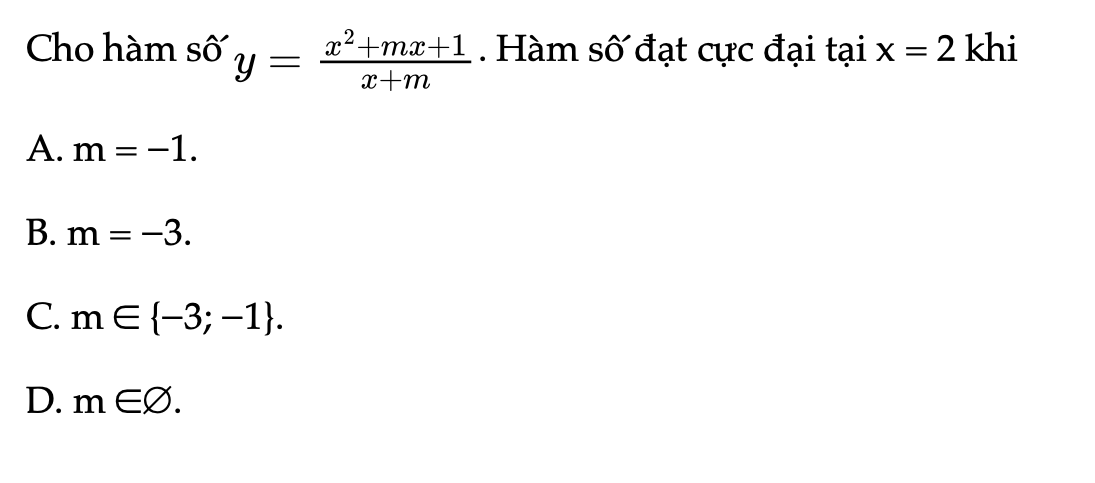
Bài 1.55 trang 34 SBT Toán 12 Tập 1
Cho hàm số sau. Hàm số đạt cực đại tại x = 2 khi?

Bài 1.56 trang 34 SBT Toán 12 Tập 1
Cho hàm số y có đồ thị (C). Xét các mệnh đề sau. Số mệnh đề đúng trong các mệnh đề trên là?

Bài 1.57 trang 34 SBT Toán 12 Tập 1
Cho hàm số y. Xét các mệnh đề sau. Số mệnh đề đúng trong các mệnh đề trên là?

Bài 1.58 trang 34 SBT Toán 12 Tập 1
Cho hàm số y. Mệnh đề nào sau đây là đúng?
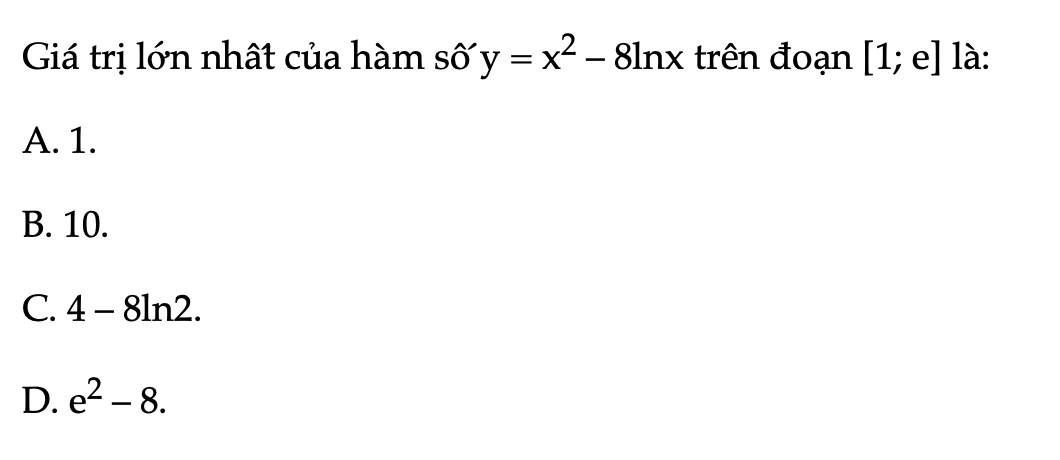
Bài 1.59 trang 34 SBT Toán 12 Tập 1
Giá trị lớn nhất của hàm số y = x^2 – 8lnx trên đoạn [1; e] là:
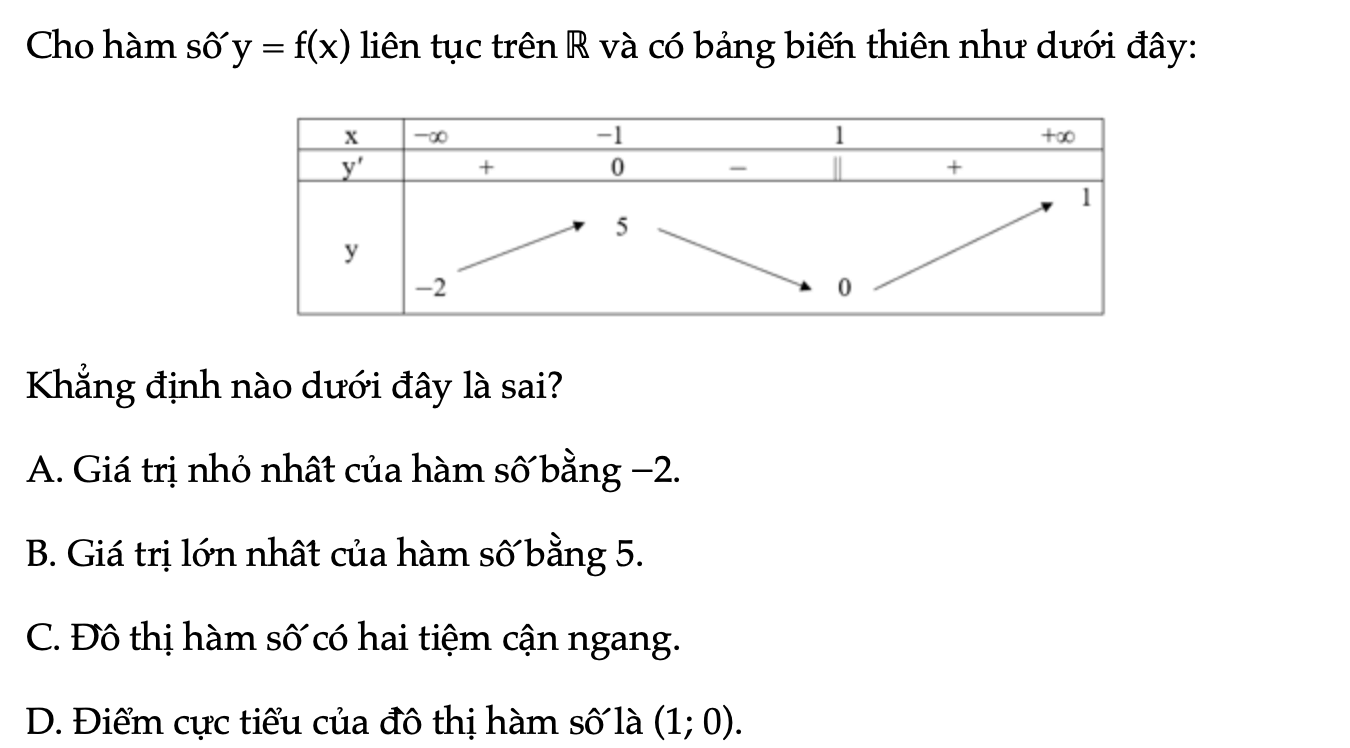
Bài 1.60 trang 35 SBT Toán 12 Tập 1
ho hàm số y = f(x) liên tục trên ℝ và có bảng biến thiên như dưới đây. Khẳng định nào dưới đây là sai?
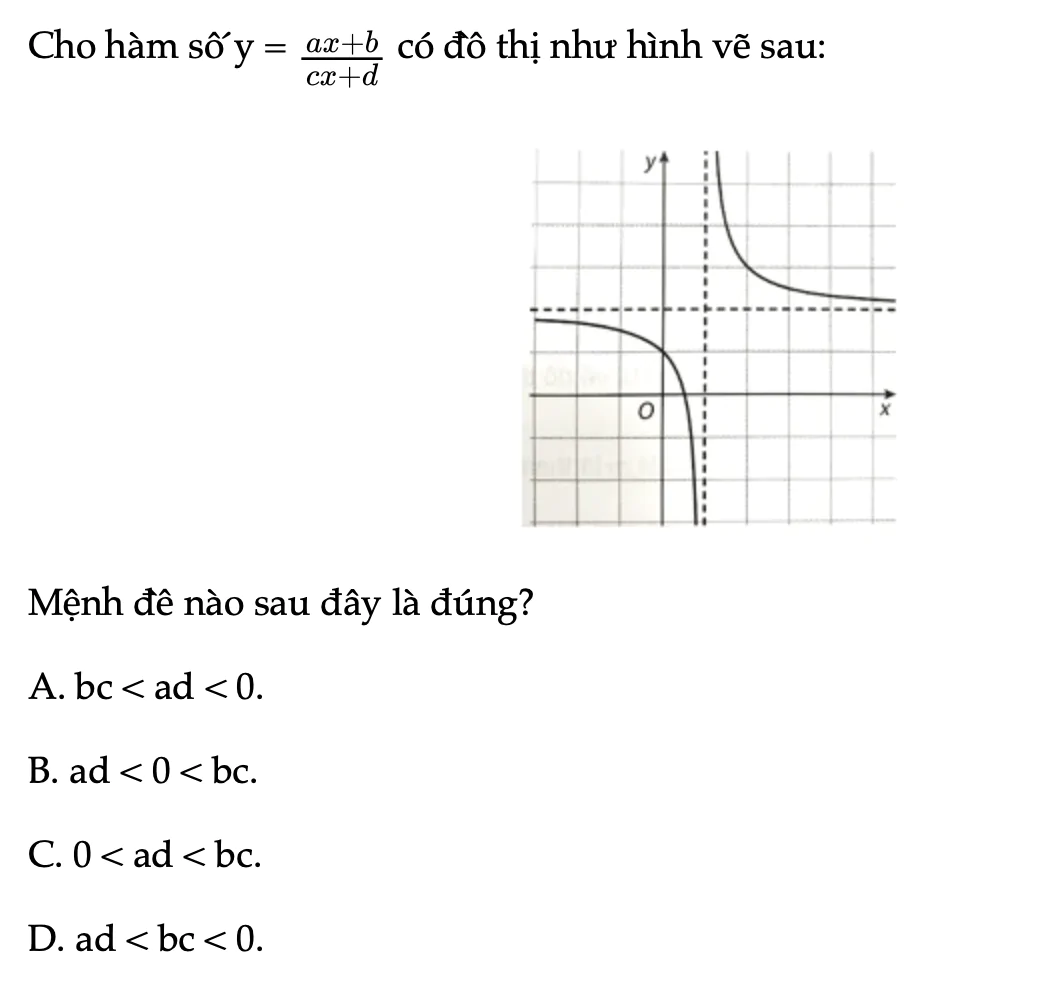
Bài 1.61 trang 35 SBT Toán 12 Tập 1
Cho hàm số y có đồ thị như hình vẽ sau. Mệnh đề nào sau đây là đúng?

Bài 1.62 trang 35 SBT Toán 12 Tập 1
Biết đường thẳng y = 2x – 3 cắt đồ thị hàm số y tại hai điểm A và B. Tọa độ trung điểm I của đoạn thẳng AB là?

Bài 1.63 trang 36 SBT Toán 12 Tập 1
Cho hàm số y. Thực hiện các yêu cầu bài toán.

Bài 1.64 trang 36 SBT Toán 12 Tập 1
Cho hàm số y có đồ thị (C). Thực hiện các yêu cầu sau.

Bài 1.65 trang 36 SBT Toán 12 Tập 1
Cho hàm số y. Thực hiện các yêu cầu sau.

Bài 1.66 trang 36 SBT Toán 12 Tập 1
Cho hàm số y với m là tham số. Thực hiện các yêu cầu sau.
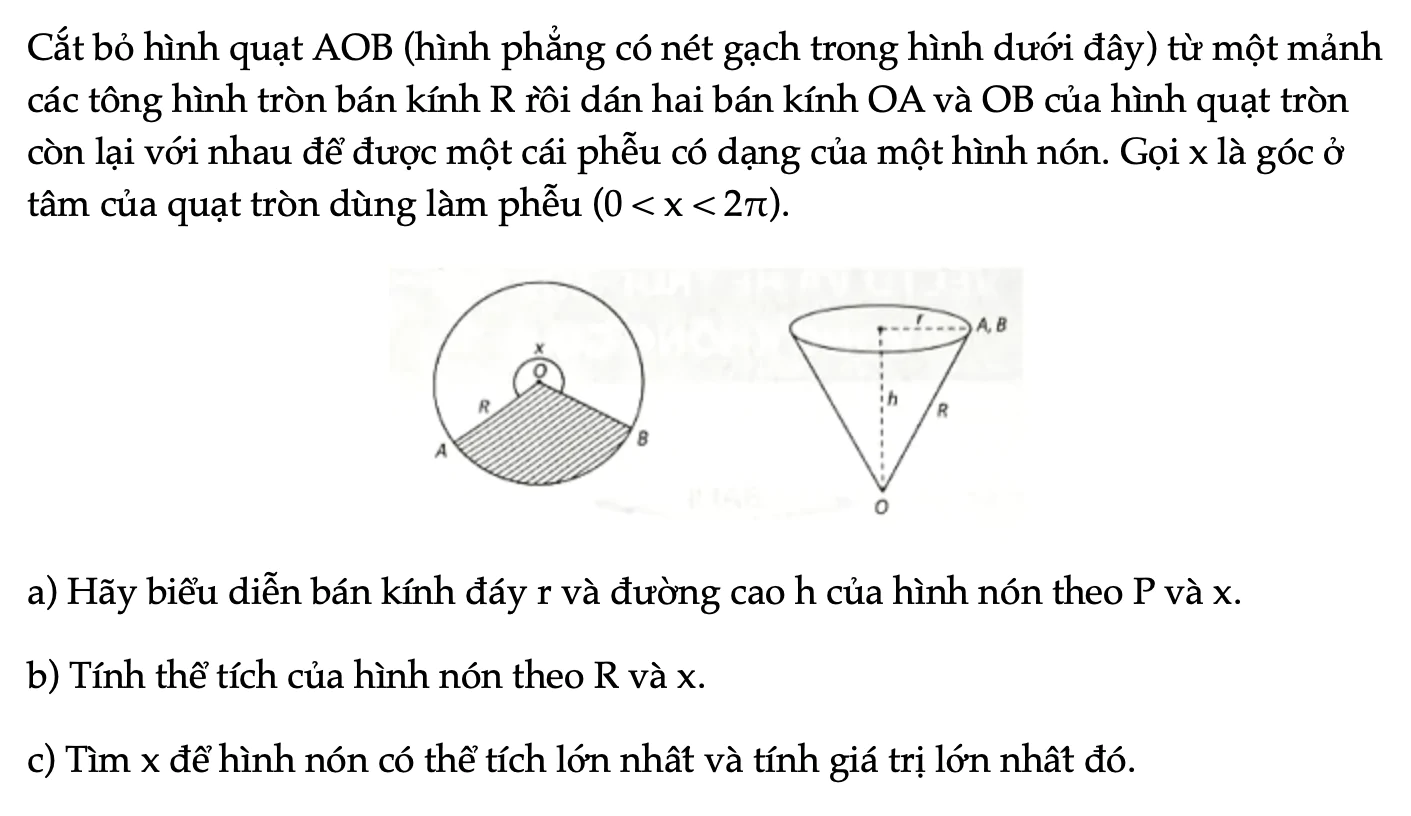
Bài 1.67 trang 36 SBT Toán 12 Tập 1
Cắt bỏ hình quạt AOB (hình phẳng có nét gạch trong hình dưới đây) từ một mảnh các tông hình tròn bán kính R rồi dán hai bán kính OA và OB của hình quạt tròn còn lại với nhau để được một cái phễu có dạng của một hình nón. Gọi x là góc ở tâm của quạt tròn d

Bài 1.68 trang 37 SBT Toán 12 Tập 1
Một hành lang giữa hai nhà có hình dạng một lăng trụ đứng (xem hình bên). Hai mặt bên ABB'A' và ACC'A' là hai tấm kính hình chữ nhật dài 20 m, rộng 5 m. Gọi x (m) là độ dài của cạnh BC.