Giải bài tập Bài 1.8 trang 9 SBT Toán 12 Tập | SBT Toán 12 - Kết nối tri thức (SBT)
Hướng dẫn giải chi tiết từng bước bài tập Bài 1.8 trang 9 SBT Toán 12 Tập . Bài 1. Tính đơn điệu và cực trị của hàm số.. SBT Toán 12 - Kết nối tri thức (SBT)
Đề bài:
Hàm chi phí và hàm doanh thu (đều tính bằng triệu đồng) của một loại sản phẩm lần lượt là C(x) = 25,5x + 1 000 và R(x) = 75,5x, trong đó x là số đơn vị sản phẩm đó được sản xuất và bán ra.
a) Tính hàm lợi nhuận trung bình
b) Tìm lợi nhuận trung bình khi mức sản xuất x lần lượt là 100, 500 và 1 000 đơn vị sản phẩm.
c) Xét tính đơn điệu của hàm lợi nhuận trung bình trên khoảng (0; +∞) và tính giới hạn của hàm số này khi x → +∞. Giải thích ý nghĩa thực tiễn của kết quả nhận được.
Đáp án và cách giải chi tiết:
a) Ta có:
(triệu đồng).
Tập xác định của hàm lợi nhuận trung bình là: (0; +∞).
b) Với x = 100 thì (triệu đồng).
Với x = 500 thì (triệu đồng).
Với x = 1 000 thì (triệu đồng).
c) Ta có:
với mọi x ∈ (0; +∞).
Vậy hàm lợi nhuận trung bình đồng biến trên khoảng (0; +∞).
Mặt khác,
Ta có bảng biến thiên như sau:
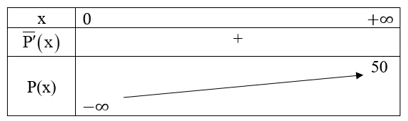
Như vậy, mặc dù lợi nhuận trung bình luôn tăng khi mức sản xuất tăng nhưng không vượt quá 50 triệu đồng.
Nguồn: loigiaitoan.com
Tổng số đánh giá:
Xếp hạng: / 5 sao
Bài tập liên quan:
Bài 1.1 trang 8 SBT Toán 12 Tập 1
Cho hàm f(x) xác định trên ℝ và đạo hàm f'(x) có đồ thị như hình bên. Sử dụng đồ thị hàm số y = f'(x), hãy cho biết:

a) Các khoảng đồng biến, khoảng nghịch biến của hàm số f(x);
b) Hàm số f(x) có cực đại, cực tiểu không? Nếu có, hãy cho biết các điểm cực trị tương ứng.
Bài 1.2 trang 9 SBT Toán 12 Tập 1
Tìm các khoảng đồng biến, khoảng nghịch biến và cực trị (nếu có) của các hàm số sau:
a) y = x3 – 9x2 – 48x + 52;
b) y = −x3 + 6x2 + 9.
Bài 1.3 trang 9 SBT Toán 12 Tập 1
Xét tính đơn điệu và tìm các cực trị (nếu có) của các hàm số sau:
a)
b)
Bài 1.4 trang 9 SBT Toán 12 Tập 1
Tìm các khoảng đơn điệu và các cực trị (nếu có) của các hàm số sau:
a) y = x4 – 2x2 + 3;
b) y = x2lnx.
Bài 1.5 trang 9 SBT Toán 12 Tập 1
Tìm các giá trị của tham số m sao cho hàm số y = x3 + mx2 + 3x + 2 đồng biến trên ℝ.
Bài 1.6 trang 9 SBT Toán 12 Tập 1
Chứng minh rằng hàm số không có đạo hàm tại x = 0 nhưng có cực tiểu tại điểm x = 0.
Bài 1.7 trang 9 SBT Toán 12 Tập 1
Một nhà phân phối đồ chơi trẻ em xác định hàm chi phí C(x) và hàm doanh thu R(x) (đều tính bằng trăm nghìn đồng) cho một loại đồ chơi như sau:
C(x) = 1,2x – 0,0001x2, 0 ≤ x ≤ 6 000,
R(x) = 3,6x – 0,0005x2, 0 ≤ x ≤ 6 000,
trong đó x là số lượng đồ chơi loại đó được sản xuất và bán ra. Xác định khoảng của x để hàm lợi nhuận P(x) = R(x) – C(x) đồng biến trên khoảng đó. Giải thích ý nghĩa thực tiễn và kết quả nhận được.
Bài 1.9 trang 10 SBT Toán 12 Tập 1
Một con lắc lò xo, gồm một vật nặng có khối lượng 1 kg được gắn vào một lò xo được cố định một đầu, dao động điều hòa với biên độ A = 0,24 m và chu kì T = 4 giây. Vị trí x (mét) của vật tại thời điểm t được xác định bởi x(t) = A cos(ωt), trong đó là tần số góc và thời gian t tính bằng giây.
a) Tìm vị trí của vật tại thời điểm t và tại thời điểm t = 0,5 giây.
b) Tìm vận tốc v của vật tại thời điểm t giây và tìm vận tốc của vật khi t = 0,5 giây.
c) Tìm gia tốc a của vật.
d) Sử dụng Định luật thứ hai của Newton F = ma, tìm độ lớn và hướng của lực tác dụng lên vật khi t = 0,5 giây.
e) Tìm thời gian tối thiểu để vật chuyển động từ vị trí ban đầu đến vị trí x = −0,12 m. Tìm vận tốc của vật khi x = −0,12 m.
Bài 1.10 trang 10 SBT Toán 12 Tập 1
Một vật chuyển động dọc theo trục số nằm ngang, chiều dương từ trái sang phải. Giả sử vị trí của vật x (mét) từ thời điểm t = 0 giây đến thời điểm t = 5 giây được cho bởi công thức x(t) = t3 – 7t2+ 11t + 5.
a) Xác định vận tốc v của vật. Xác định khoảng thời gian vật chuyển động sang phải và khoảng thời gian vật chuyển sang trái.
b) Tìm tốc độ của vật và thời điểm vật dừng lại. Tính tốc độ cực đại của vật và khoảng thời gian từ t = 1 giây đến t = 4 giây.
c) Xác định gia tốc a của vật. Tìm khoảng thời gian vật tăng tốc và khoảng thời gian vật giảm tốc.