Giải bài tập Bài 1.32 trang 25 SBT Toán 12 Tập 1 | SBT Toán 12 - Kết nối tri thức (SBT)
Hướng dẫn giải chi tiết từng bước bài tập Bài 1.32 trang 25 SBT Toán 12 Tập 1. Bài 4. Khảo sát sự biến thiên và vẽ đồ thị của hàm số.. SBT Toán 12 - Kết nối tri thức (SBT)
Đề bài:
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau:
a)
b)
Đáp án và cách giải chi tiết:
a)
1. Tập xác định: D = ℝ\{−2}.
2. Sự biến thiên
Giới hạn tại vô cực:
Do đó, đường thẳng y = 3 là đường tiệm cận ngang của đồ thị hàm số.
Do đó, đường thẳng x = −2 là đường tiệm cận đứng của đồ thị hàm số.
Ta có: y' = > 0, với mọi x ∈ D.
Ta có bảng biến thiên như sau:
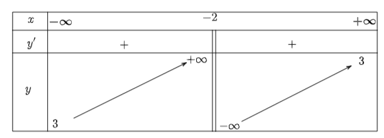
Hàm số đồng biến trên khoảng (−∞; −2) và (−2; +∞).
2. Đồ thị hàm số
Đồ thị cắt trục tung tại điểm
Đồ thị cắt trục hoành tại điểm
Đồ thị có tâm đối xứng là điểm (−2; 3).
Hai trục đối xứng của đồ thị hàm số là hai đường phân giác của các góc tạo bởi hai đường tiệm cận.
Đồ thị hàm số như sau:
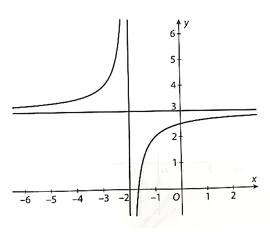
b)
1. Tập xác định: D = ℝ\{1}.
2. Sự biến thiên
Giới hạn tại vô cực:
Do đó, đường thẳng y = 2 là đường tiệm cận ngang của đồ thị hàm số.
Do đó, đường thẳng x = 1 là đường tiệm cận đứng của đồ thị hàm số.
Ta có: y' = > 0, với mọi x ∈ D.
Ta có bảng biến thiên như sau:
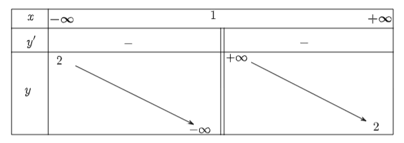
Hàm số nghịch biến trên các khoảng (−∞; 1) và (1; +∞).
3. Đồ thị hàm số
Đồ thị hàm số cắt trục tung tại điểm (0; 1).
Đồ thị hàm số cắt trục hoành tại điểm
Đồ thị hàm số có tâm đối xứng là điểm (1; 2).
Hai trục đối xứng của đồ thị hàm số là hai đường phân giác của các góc tạo bởi hai đường tiệm cận.
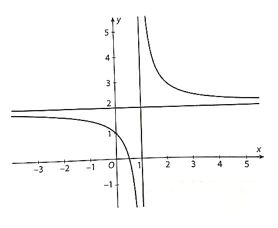
Nguồn: loigiaitoan.com
Tổng số đánh giá:
Xếp hạng: / 5 sao
Bài tập liên quan:
Bài 1.31 trang 25 SBT Toán 12 Tập 1
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau:
a) y = x3 – 6x2 + 9x;
b) y = x3 + 3x2 + 6x + 4.
Bài 1.33 trang 25 SBT Toán 12 Tập 1
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau:
a)
b)
Bài 1.34 trang 25 SBT Toán 12 Tập 1
Cho hàm số y = f(x) có đạo hàm f'(x) xác định trên ℝ và f'(x) có đồ thị như hình vẽ sau:
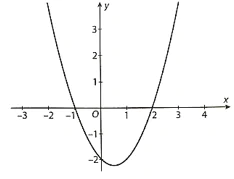
Tìm các khoảng đồng biến, khoảng nghịch biến và các điểm cực trị của hàm số y = f(x).
Bài 1.35 trang 25 SBT Toán 12 Tập 1
Gia tốc a(t) của một vật chuyển động, t tính theo giây, từ giây thứ nhất đến giây thứ 5 là một hàm liên tục có đồ thị như hình sau:

a) Lập bảng biến thiên của hàm vận tốc y = v(t) của vật, với t ∈ [1; 5].
b) Tại thời điểm nào vật chuyển động với vận tốc lớn nhất?
Bài 1.36 trang 26 SBT Toán 12 Tập 1
Một mẫu giấy in hình chữ nhật được thiết kế với vùng in có diện tích 300 cm2, lề trái và lề phải là 2 cm, lề trên và lề dưới là 3 cm. Gọi x (cm) là chiều rộng của tờ giấy.
a) Tính diện tích của tờ giấy theo x.
b) Kí hiệu diện tích tờ giấy là S(x). Khảo sát sự biến thiên của hàm số y = S(x).
c) Tìm kích thước của tờ giấy sao cho nguyên liệu giấy được sử dụng là ít nhất.
Bài 1.37 trang 26 SBT Toán 12 Tập 1
Giả sử chi phí để sản xuất x sản phẩm của một nhà máy được cho bởi C(x) = 0,2x2 + 10x + 5(triệu đồng). Khi đó, chi phí trung bình để sản xuất một đơn vị sản phẩm là
a) Khảo sát sự biến thiên của hàm số y = f(x).
b) Số lượng sản phẩm cần sản xuất là bao nhiêu để chi phí trung bình là thấp nhất?
Bài 1.38 trang 26 SBT Toán 12 Tập 1
Cho điểm A(3;2 ) trên mặt phẳng tọa độ. Một đường thẳng đi qua A cắt trục hoành tại B, cắt trục tung tại C tạo thành một tam giác OBC nằm trong góc phần tư thứ nhấ, với O là gốc tọa độ.

a) Biết hoành độ điểm B là x = t với t > 3. Tính diện tích tam giác OBC theo t. Kí hiệu diện tích này là S(t).
b) Khảo sát sự biến thiên của hàm số S(t).
c) Tìm vị trí điểm B để diện tích tam giác OBC là nhỏ nhất.
Bài 1.39 trang 26 SBT Toán 12 Tập 1
Một quần thể cá được nuôi trong một hồ nhân tạo lúc ban đầu có 80 000 con. Sau t năm, số lượng quần thể cá nói trên được xác định bởi
(nghìn con).
a) Khảo sát sự biến thiên của hàm số y = N(t).
b) Số lượng tối đa có thể có của quần thể cá là bao nhiêu?
Bài 1.40 trang 27 SBT Toán 12 Tập 1
Một khối bưu kiện hình hộp chữ nhật được quy định về kích cỡ như sau: tổng chiều dài và chu vi thiết diện ngang (hình vuông) là 240 cm.
Gọi x là độ dài cạnh của thiết diện ngang.
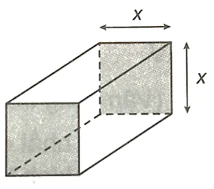
a) Tính thể tích của khối bưu kiện theo x.
b) Kí hiệu V(x) là thể tích của khối bưu kiện. Khảo sát sự biến thiên của hàm số y = V(x).