Giải bài tập Bài 1.67 trang 36 SBT Toán 12 Tập 1 | SBT Toán 12 - Kết nối tri thức (SBT)
Hướng dẫn giải chi tiết từng bước bài tập Bài 1.67 trang 36 SBT Toán 12 Tập 1. Bài tập cuối chương 1. SBT Toán 12 - Kết nối tri thức (SBT)
Đề bài:
Cắt bỏ hình quạt AOB (hình phẳng có nét gạch trong hình dưới đây) từ một mảnh các tông hình tròn bán kính R rồi dán hai bán kính OA và OB của hình quạt tròn còn lại với nhau để được một cái phễu có dạng của một hình nón. Gọi x là góc ở tâm của quạt tròn dùng làm phễu (0 < x < 2π).

a) Hãy biểu diễn bán kính đáy r và đường cao h của hình nón theo P và x.
b) Tính thể tích của hình nón theo R và x.
c) Tìm x để hình nón có thể tích lớn nhất và tính giá trị lớn nhất đó.
Đáp án và cách giải chi tiết:
a) Vì độ dài của đường tròn đáy hình nón bằng độ dài của quạt tròn dùng làm phễu nên ta có: 2πr = Rx ⇔ r =
Mặt khác h =
b) Thể tích của hình nón là:
, 0 < x < 2π.
c) Ta cần tìm x ∈ (0; 2π) sao cho thể tích V đạt giá trị lớn nhất.
Xét hàm số f(x) = , x ∈ (0; 2π).
Ta có: f'(x) =
f'(x) = 0 ⇔ x = ≈ 1,63π.
Ta có bảng biến thiên như sau:
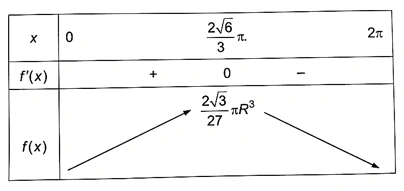
Hình nón có thể tích lớn nhất khi x = ≈ 1,63π.
Khi đó:
Nguồn: loigiaitoan.com
Tổng số đánh giá:
Xếp hạng: / 5 sao
Bài tập liên quan:
Bài 1.51 trang 33 SBT Toán 12 Tập 1
Cho hàm số y = f(x) có đạo hàm trên (a;b). Xét các mệnh đề sau:
(I) Nếu f'(x) ≥ 0 với mọi x ∈ (a; b) và dấu bằng chỉ xảy ra tại một số hữu hạn điểm trên
(a; b) thì hàm số đồng biến trên (a; b).
(II) Nếu f'(x) ≤ 0 với mọi x ∈ (a; b) và dấu bằng chỉ xảy ra tại một số hữu hạn điểm trên (a; b) thì hàm số nghịch biến trên (a; b).
(III) Nếu f'(x) ≤ 0 với mọi x ∈ (a; b) thì hàm số nghịch biến trên khoảng (a; b).
(IV) Nếu f'(x) ≥ 0 với mọi x ∈ (a; b) thì hàm số đồng biến trên khoảng (a; b).
Trong các mệnh để trên, mệnh đề nào đúng, mệnh đề nào sai?
A. I, II, III và IV đúng.
B. I, II và III đúng, còn IV sai.
C. I, II và IV đúng, còn III sai.
D. I và II đúng, còn III và IV sai.
Bài 1.52 trang 33 SBT Toán 12 Tập 1
Hàm số nào dưới đây nghịch biến trên tập xác định của nó?
A. y = −x3 + 3x2 + 9x.
B.
C.
D. y = 2024lnx.
Bài 1.53 trang 33 SBT Toán 12 Tập 1
Có tất cả bao nhiêu giá trị nguyên dương của tham số m để hàm số đồng biến trên từng khoảng xác định của nó?
A. 2 021.
B. 2 024.
C. 2 023.
D. 2 022.
Bài 1.54 trang 34 SBT Toán 12 Tập 1
Cho hàm số y = f(x) có đạo hàm f'(x) = x(x – 1)2(x + 2)4 với mọi x ∈ ℝ. Số điểm cực trị của hàm số đã cho là:
A. 0.
B. 1.
C. 2.
D. 3.
Bài 1.55 trang 34 SBT Toán 12 Tập 1
Cho hàm số . Hàm số đạt cực đại tại x = 2 khi
A. m = −1.
B. m = −3.
C. m ∈ {−3; −1}.
D. m ∈∅.
Bài 1.56 trang 34 SBT Toán 12 Tập 1
Cho hàm số có đồ thị (C). Xét các mệnh đề sau:
(I): Điểm cực đại của đồ thị (C) là (0; 1).
(II): Trục hoành là tiệm cận ngang của đồ thị (C).
(III): Giá trị lớn nhất của hàm số là 1.
(IV): Điểm cực đại của đồ thị (C) là x = 0.
Số mệnh đề đúng trong các mệnh đề trên là:
A. 4.
B. 1.
C. 2.
D. 3.
Bài 1.57 trang 34 SBT Toán 12 Tập 1
Cho hàm số y = . Xét các mệnh đề sau:
(I) Hàm số nghịch biến trên tập xác định của nó.
(II) Trục hoành là tiệm cận ngang của đồ thị hàm số.
(III) Trục tung là tiệm cận đúng của đồ thị hàm số.
(IV) Hàm số không có cực trị.
Số mệnh đề đúng trong các mệnh đề trên là:
A. 3.
B. 1.
C. 2.
D. 4.
Bài 1.58 trang 34 SBT Toán 12 Tập 1
Cho hàm số Mệnh đề nào sau đây là đúng?
A. Đường thẳng x = 1 là tiệm cận đứng của đồ thị hàm số.
B. Đồ thị hàm số có hai đường tiệm cận đứng.
C. Đồ thị hàm số không có tiệm cận ngang.
D. Đường thẳng x = 5 là tiệm cận đứng của đồ thị hàm số.
Bài 1.59 trang 34 SBT Toán 12 Tập 1
Giá trị lớn nhất của hàm số y = x2 – 8lnx trên đoạn [1; e] là:
A. 1.
B. 10.
C. 4 – 8ln2.
D. e2 – 8.
Bài 1.60 trang 35 SBT Toán 12 Tập 1
Cho hàm số y = f(x) liên tục trên ℝ và có bảng biến thiên như dưới đây:

Khẳng định nào dưới đây là sai?
A. Giá trị nhỏ nhất của hàm số bằng −2.
B. Giá trị lớn nhất của hàm số bằng 5.
C. Đồ thị hàm số có hai tiệm cận ngang.
D. Điểm cực tiểu của đồ thị hàm số là (1; 0).
Bài 1.61 trang 35 SBT Toán 12 Tập 1
Cho hàm số y = có đồ thị như hình vẽ sau:

Mệnh đề nào sau đây là đúng?
A. bc < ad < 0.
B. ad < 0 < bc.
C. 0 < ad < bc.
D. ad < bc < 0.
Bài 1.62 trang 35 SBT Toán 12 Tập 1
Biết đường thẳng y = 2x – 3 cắt đồ thị hàm số y = tại hai điểm A và B. Tọa độ trung điểm I của đoạn thẳng AB là:
A.
B.
C.
D.
Bài 1.63 trang 36 SBT Toán 12 Tập 1
Cho hàm số y = x3 + (m – 1)x2 + (2m – 3)x + .
a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số khi m = 2.
b) Tìm m để hàm số có hai điểm cực trị x1 và x2 thỏa mãn
c) Tìm m để hàm số đồng biến trên ℝ.
d) Tìm m để hàm số đồng biến trên khoảng (1; +∞).
Bài 1.64 trang 36 SBT Toán 12 Tập 1
Cho hàm số y = x3 – 3x2 + 2 có đồ thị (C).
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số đã cho.
b) Viết phương trình tiếp tuyến ∆ của đồ thị (C) tại tâm đối xứng của nó. Chứng minh rằng ∆ là tiếp tuyến có hệ số góc nhỏ nhất của (C).
c) Tìm các giá trị của tham số m để phương trình x3 – 3x2 – m = 0 có ba nghiệm phân biệt.
Bài 1.65 trang 36 SBT Toán 12 Tập 1
Cho hàm số
a) Tìm m để tiệm cận ngang của đồ thị hàm số đi qua điểm (1; 2).
b) Khảo sát và vẽ đồ thị (H) của hàm số y = f(x) với m tìm được ở câu a.
c) Từ đồ thị (H) của hàm số y = f(x) ở câu b, vẽ đồ thị của hàm số y = .
Bài 1.66 trang 36 SBT Toán 12 Tập 1
Cho hàm số với m là tham số.
a) Chứng minh rằng hàm số đã cho luôn có cực đại, cực tiểu với mọi m > 0.
b) Khảo sát và vẽ đồ thị (H) của hàm số đã cho với m = 1.
c) Giả sử ∆ cắt tiệm cận đứng và tiệm cận xiên của (H) tại điểm M ∈ (H) bất kì. Chứng minh rằng nếu ∆ cắt tiệm cận đứng và tiệm cận xiên của (H) tại A và B thì M luôn là trung điểm của đoạn AB.
Bài 1.68 trang 37 SBT Toán 12 Tập 1
Một hành lang giữa hai nhà có hình dạng một lăng trụ đứng (xem hình bên). Hai mặt bên ABB'A' và ACC'A' là hai tấm kính hình chữ nhật dài 20 m, rộng 5 m. Gọi x (m) là độ dài của cạnh BC.

a) Tính thể tích V của hình lăng trụ theo x.
b) Tìm x sao cho hình lăng trụ có thể tích lớn nhất và tính giá trị lớn nhất đó.