Giải bài tập Toán 11 Chương 8: Quan hệ vuông góc trong không gian | Chân trời sáng tạo
Hướng dẫn giải Chương 8: Quan hệ vuông góc trong không gian
Giải bài tập Bài 1: Hai đường thẳng vuông góc

Bài 1 trang 56 Toán 11 Tập 2
Cho hình chóp S.ABCD có đáy là hình thoi ABCD cạnh a. Cho biết SA ⊥ AB và SA ⊥ AD. Tính góc giữa SB và CD, SD và CB. Bài 1 trang 56 Toán 11 Tập 2

Bài 2 trang 56 Toán 11 Tập 2
Cho tứ diện đều ABCD. Chứng minh rằng AB ⊥ CD. Bài 2 trang 56 Toán 11 Tập 2
Bài 3 trang 56 Toán 11 Tập 2
Cho hình chóp S.ABC có SA = SB = SC = a. Cho I và J lần lượt là trung điểm của SA và BC. Chứng minh rằng IJ ⊥ SA và IJ ⊥ BC. Bài 3 trang 56 Toán 11 Tập 2

Bài 5 trang 56 Toán 11 Tập 2
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của BC và AD. Biết AB = CD = 2a và MN = a căn 3. Tính góc giữa AB và CD. Bài 5 trang 56 Toán 11 Tập 2

Bài 4 trang 56 Toán 11 Tập 2
Cho tứ diện đều ABCD cạnh a. Gọi K là trung điểm CD. Tính góc giữa hai đường thẳng AK và BC. Bài 4 trang 56 Toán 11 Tập 2

Bài 6 trang 56 Toán 11 Tập 2
Một ô che nắng có viền khung hình lục giác đều ABCDEF song song với mặt bàn và có cạnh AB song song với cạnh bàn a (Hình 5). Tính số đo góc hợp bởi đường thẳng a lần lượt với các đường thẳng AF, AE và AD. Bài 6 trang 56 Toán 11 Tập 2

Hoạt động khởi động trang 54 Toán 11 Tập 2
Ta đã biết cách xác định góc giữa hai đường thẳng cùng thuộc một mặt phẳng. Có góc giữa hai đường thẳng chéo nhau không? Nếu có, làm thế nào để xác định?
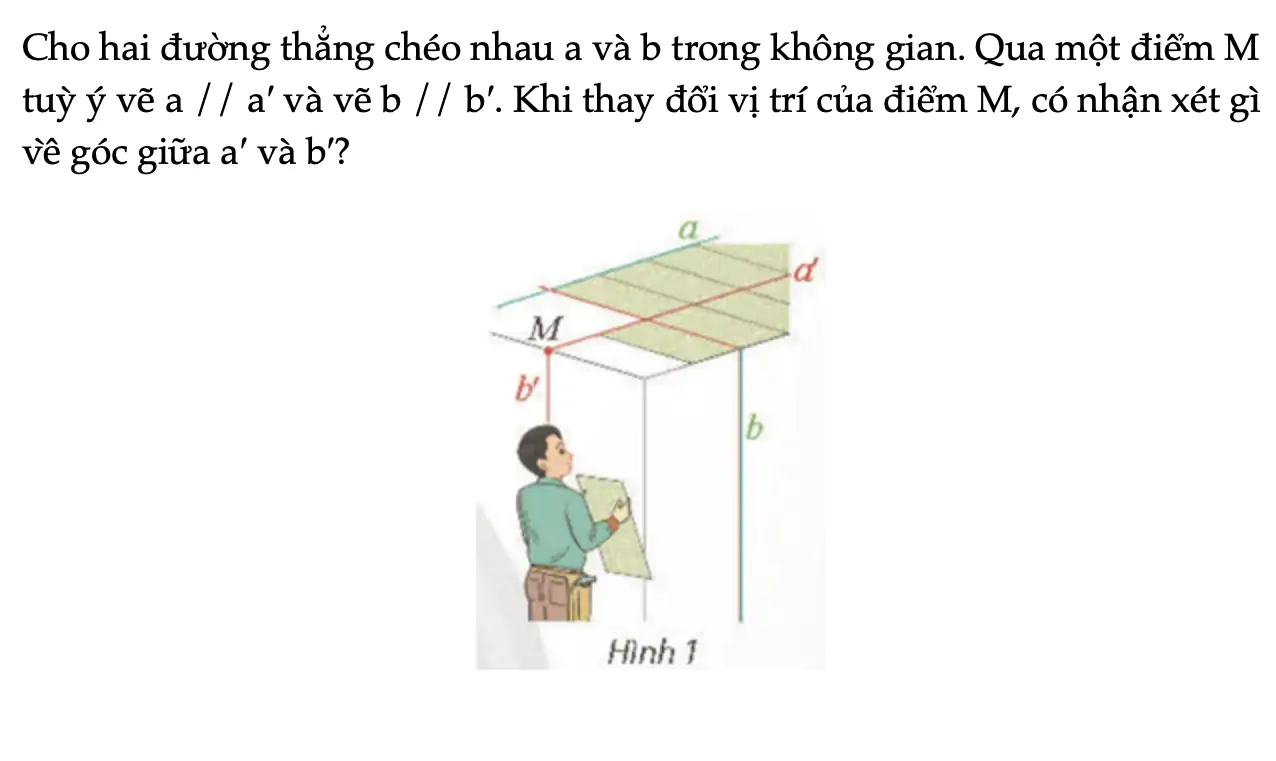
Hoạt động khám phá 1 trang 54 Toán 11 Tập 2
Cho hai đường thẳng chéo nhau a và b trong không gian. Qua một điểm M tuỳ ý vẽ a // a′ và vẽ b // b′. Khi thay đổi vị trí của điểm M, có nhận xét gì về góc giữa a′ và b′?

Thực hành 1 trang 55 Toán 11 Tập 2
Cho hình hộp ABCD.A′B′C′D′ có 6 mặt đều là hình vuông M, N, E, F lần lượt là trung điểm các cạnh BC, BA, AA′, A′D′. Tính góc giữa các cặp đường thẳng sau.

Vận dụng 1 trang 55 Toán 11 Tập 2
Khung của một mái nhà được ghép bởi các thanh gỗ như Hình 3. Cho biết tam giác OMN vuông cân tại O. Tính góc giữa hai thanh gỗ a và b.

Hoạt động khám phá 2 trang 55 Toán 11 Tập 2
Cho hình hộp ABCD.A′B′C′D′ có 6 mặt đều là hình vuông. Nêu nhận xét về góc giữa các cặp đường thẳng.

Thực hành 2 trang 55 Toán 11 Tập 2
Cho hình hộp ABCD.A′B′C′D′ có 6 mặt đều là hình vuông. a) Tìm các đường thẳng đi qua hai đỉnh của hình lập phương và vuông góc với AC . b) Trong các đường thẳng tìm được ở câu a, tìm đường thẳng chéo với AC .

Vận dụng 2 trang 55 Toán 11 Tập 2
Hình bên mô tả một người thợ đang ốp gạch vào tường có sử dụng thước laser để kẻ vạch. Tìm các đường thẳng vuông góc với đường thẳng a trong Hình 4.
Giải bài tập Bài 2: Đường thẳng vuông góc với mặt phẳng

Bài 1 trang 64 Toán 11 Tập 2
Cho hình chóp S.ABCD có SA ⊥ (ABCD). Cho biết ABCD là hình thang vuông tại A và D, AB = 2AD. Bài 1 trang 64 Toán 11 Tập 2

Bài 2 trang 64 Toán 11 Tập 2
Cho hình vuông ABCD. Gọi H, K lần lượt là trung điểm của AB, AD. Trên đường thẳng vuông góc với (ABCD) tại H, lấy điểm S. Bài 2 trang 64 Toán 11 Tập 2
Bài 3 trang 64 Toán 11 Tập 2
Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng a căn 2, có các cạnh bên đều bằng 2a. Tính góc giữa SC và AB. Bài 3 trang 64 Toán 11 Tập 2
Bài 4 trang 64 Toán 11 Tập 2
Cho hình chóp S.ABC có SA = SB = SC = a. Gọi I là trung điểm cạnh AC . Chứng minh SI ⊥ (ABC). Bài 4 trang 64 Toán 11 Tập 2

Bài 5 trang 64 Toán 11 Tập 2
Một cái lều có dạng hình lăng trụ ABC.A′B′C′ có cạnh bên AA′ vuông góc với đáy (Hình 24). Cho biết AB = AC = 2,4 m; BC = 2 m; AA′ = 3 m. Bài 5 trang 64 Toán 11 Tập 2

Hoạt động khởi động trang 57 Toán 11 Tập 2
Trong thực tế, người thợ xây dựng thường dùng dây dọi để xác định đường vuông góc với nền nhà. Thế nào là đường thẳng vuông góc với mặt phẳng?

Hoạt động khám phá 1 trang 57 Toán 11 Tập 2
Thả một dây dọi AO chạm sàn nhà tại điểm O. Kẻ một đường thẳng xOy bất kì trên sàn nhà. a) Dùng êke để kiểm tra xem AO có vuông góc với xOy không. b) Nêu nhận xét về góc giữa dây dọi và một đường thẳng bất kì trong sàn nhà.
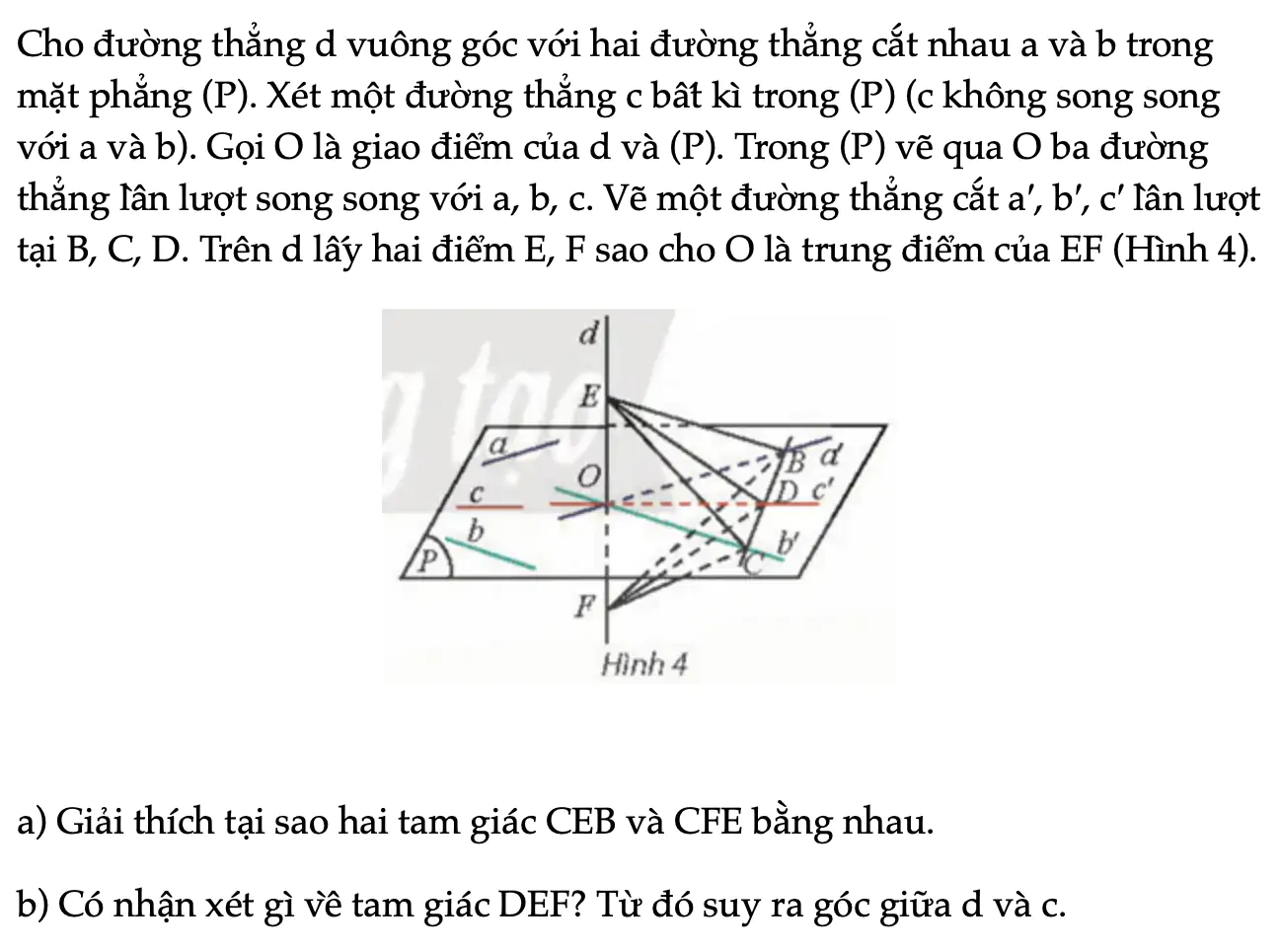
Hoạt động khám phá 2 trang 57 Toán 11 Tập 2
Cho đường thẳng d vuông góc với hai đường thẳng cắt nhau a và b trong mặt phẳng (P). Xét một đường thẳng c bất kì trong (P) (c không song song với a và b). Gọi O là giao điểm của d và (P). Trong (P) vẽ qua O ba đường thẳng lần lượt song song.
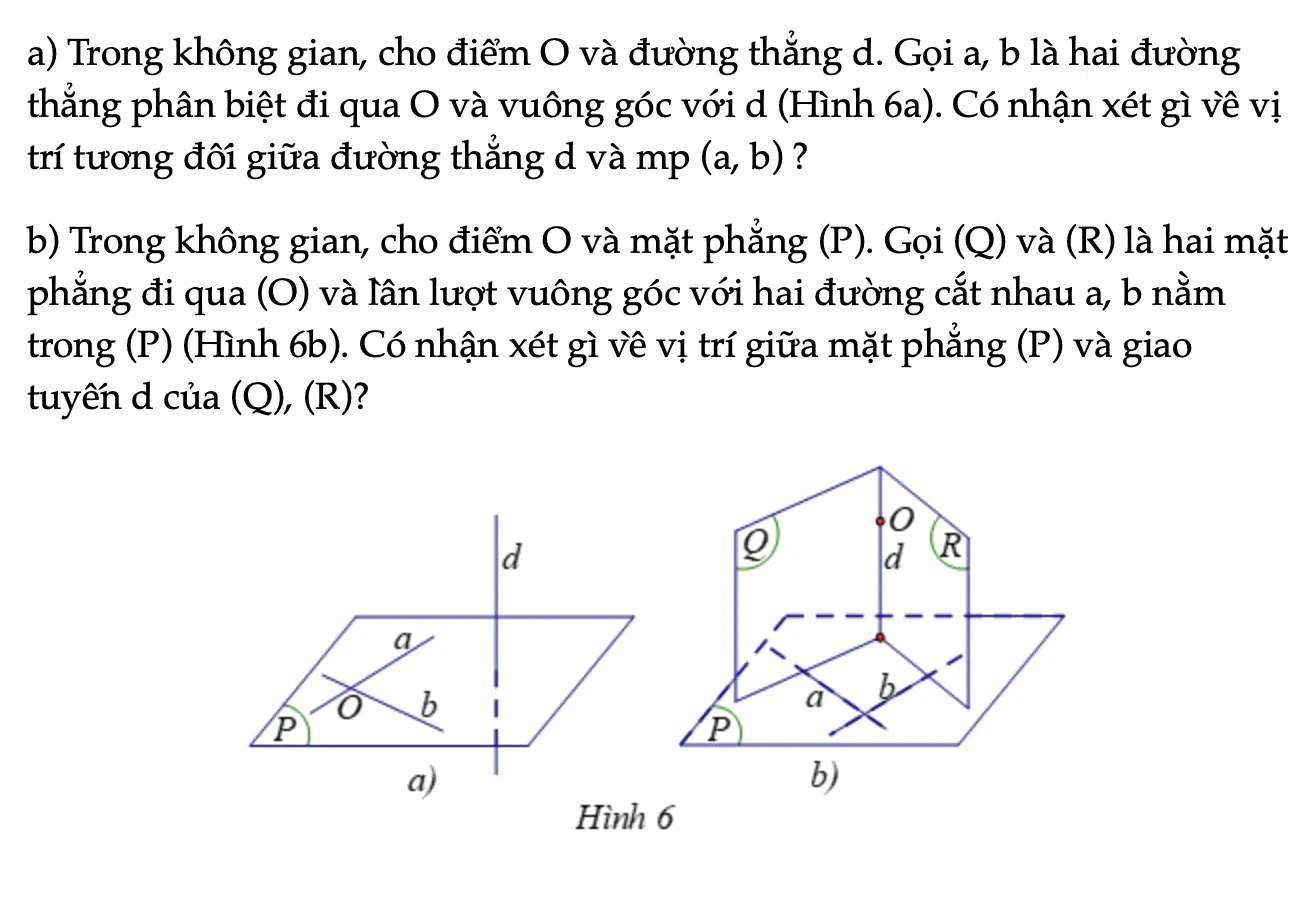
Hoạt động khám phá 3 trang 58 Toán 11 Tập 2
a) Trong không gian, cho điểm O và đường thẳng d. Gọi a, b là hai đường thẳng phân biệt đi qua O và vuông góc với d (Hình 6a). Có nhận xét gì về vị trí tương đối giữa đường thẳng d và mp (a, b) ?
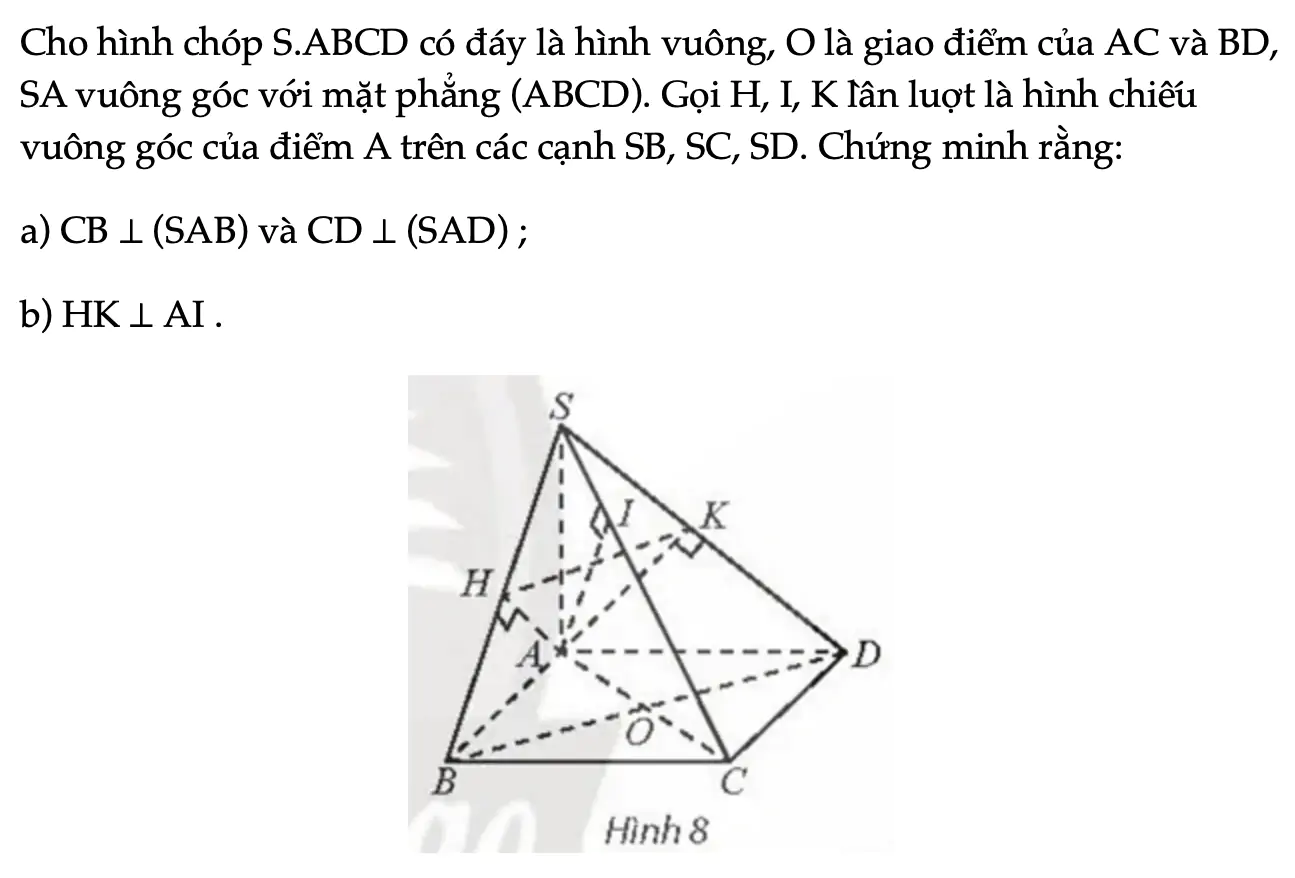
Thực hành 1 trang 59 Toán 11 Tập 2
Cho hình chóp S.ABCD có đáy là hình vuông, O là giao điểm của AC và BD, SA vuông góc với mặt phẳng (ABCD). Gọi H, I, K lần luợt là hình chiếu vuông góc của điểm A trên các cạnh SB, SC, SD. Chứng minh rằng.
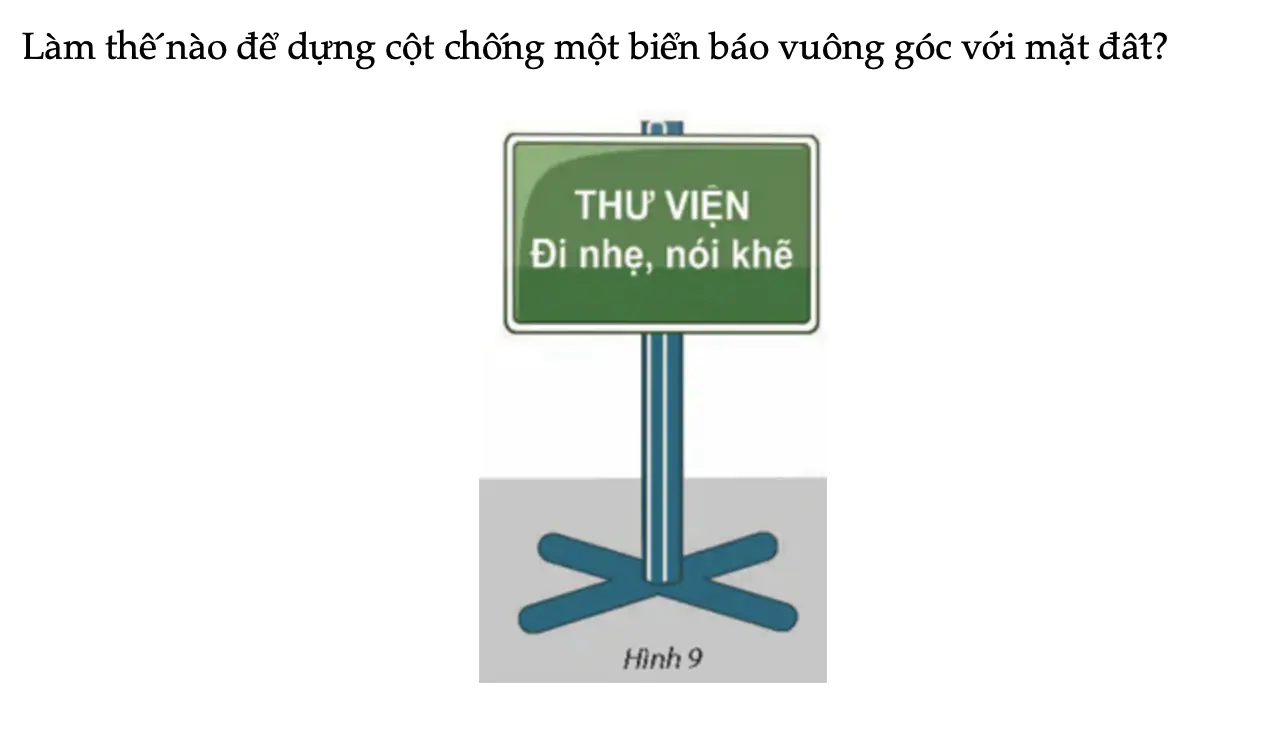
Vận dụng 1 trang 59 Toán 11 Tập 2
Làm thế nào để dựng cột chống một biển báo vuông góc với mặt đất?

Hoạt động khám phá 4 trang 60 Toán 11 Tập 2
Nêu nhận xét về vị trí tương đối của: a) Hai thân cây cùng mọc vuông góc với mặt đất. b) Mặt bàn và mặt đất cùng vuông góc với chân bàn. c) Thanh xà ngang nằm trên trần nhà và mặt sàn nhà cùng vuông góc với cột nhà.
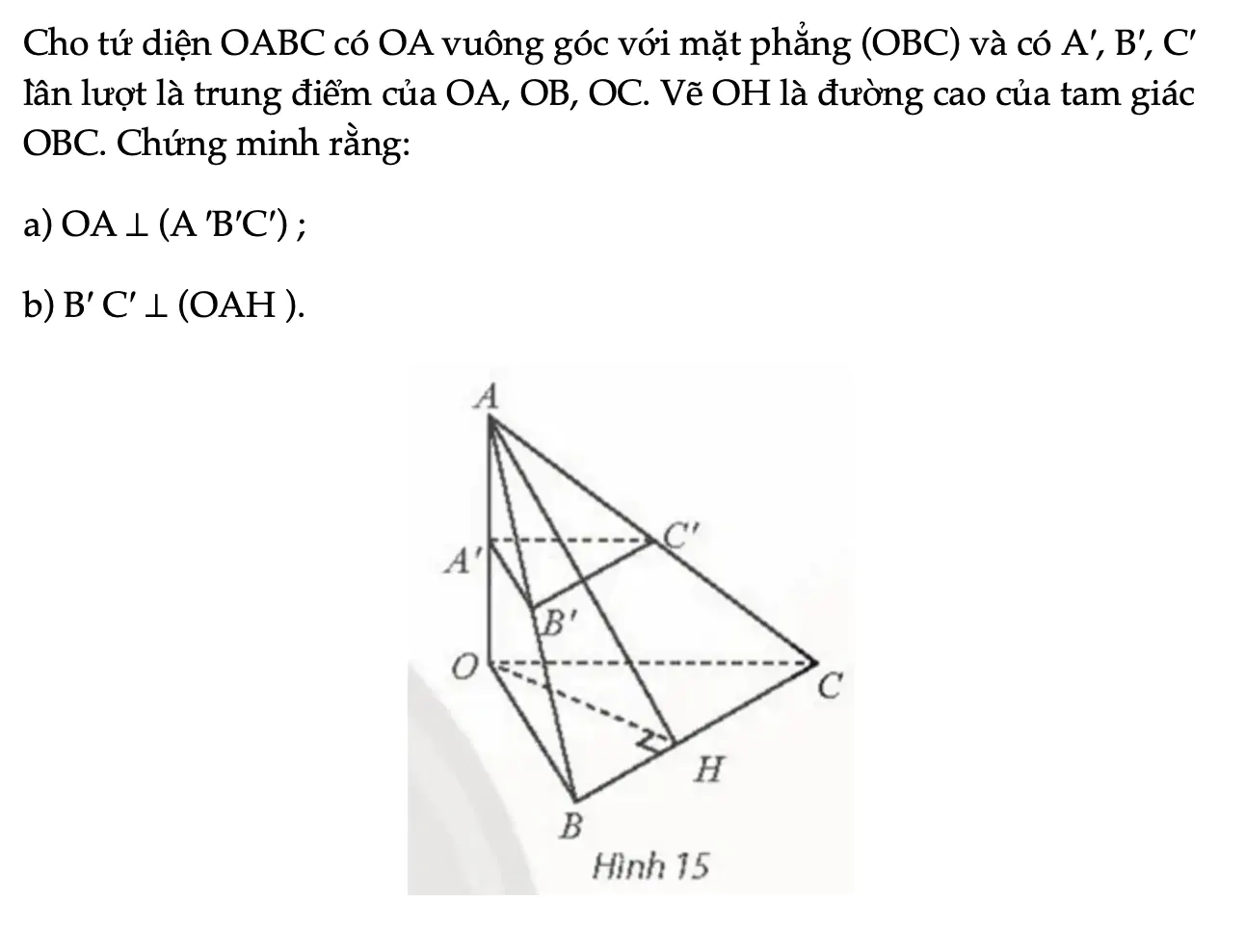
Thực hành 2 trang 61 Toán 11 Tập 2
Cho tứ diện OABC có OA vuông góc với mặt phẳng (OBC) và có A′, B′, C′ lần lượt là trung điểm của OA, OB, OC. Vẽ OH là đường cao của tam giác OBC. Chứng minh rằng: a) OA ⊥ (A ′B′C′); b) B′ C′ ⊥ (OAH ).

Thực hành 3 trang 62 Toán 11 Tập 2
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông với AB là cạnh góc vuông và có cạnh SA vuông góc với mặt phẳng (ABCD). Cho M, N, P, Q lần lượt là trung điểm của SB, AB, CD, SC. Chứng minh rằng: a) AB ⊥ (MNPQ); b) MQ ⊥ (SAB) .

Vận dụng 2 trang 62 Toán 11 Tập 2
Một kệ sách có bốn trụ chống và các ngăn làm bằng các tấm gỗ (Hình 18). Làm thế nào dùng một êke để kiểm tra xem các tấm gỗ có vuông góc với mỗi trụ chống và song song với nhau hay không? Giải thích cách làm.

Hoạt động khám phá 5 trang 62 Toán 11 Tập 2
Hai người thợ trong hình đang thả dây dọi từ một điểm M trên trần nhà và đánh dấu điểm M′ nơi đầu nhọn quả dọi chạm sàn. Có nhận xét gì về đường thẳng MM′ với mặt sàn?

Thực hành 4 trang 63 Toán 11 Tập 2
Cho hình chóp S.ABCD có SA ⊥ (ABCD) và đáy ABCD là hình chữ nhật. Xác định hình chiếu vuông góc của điểm C, đường thẳng CD và tam giác SCD trên mặt phẳng (SAB).
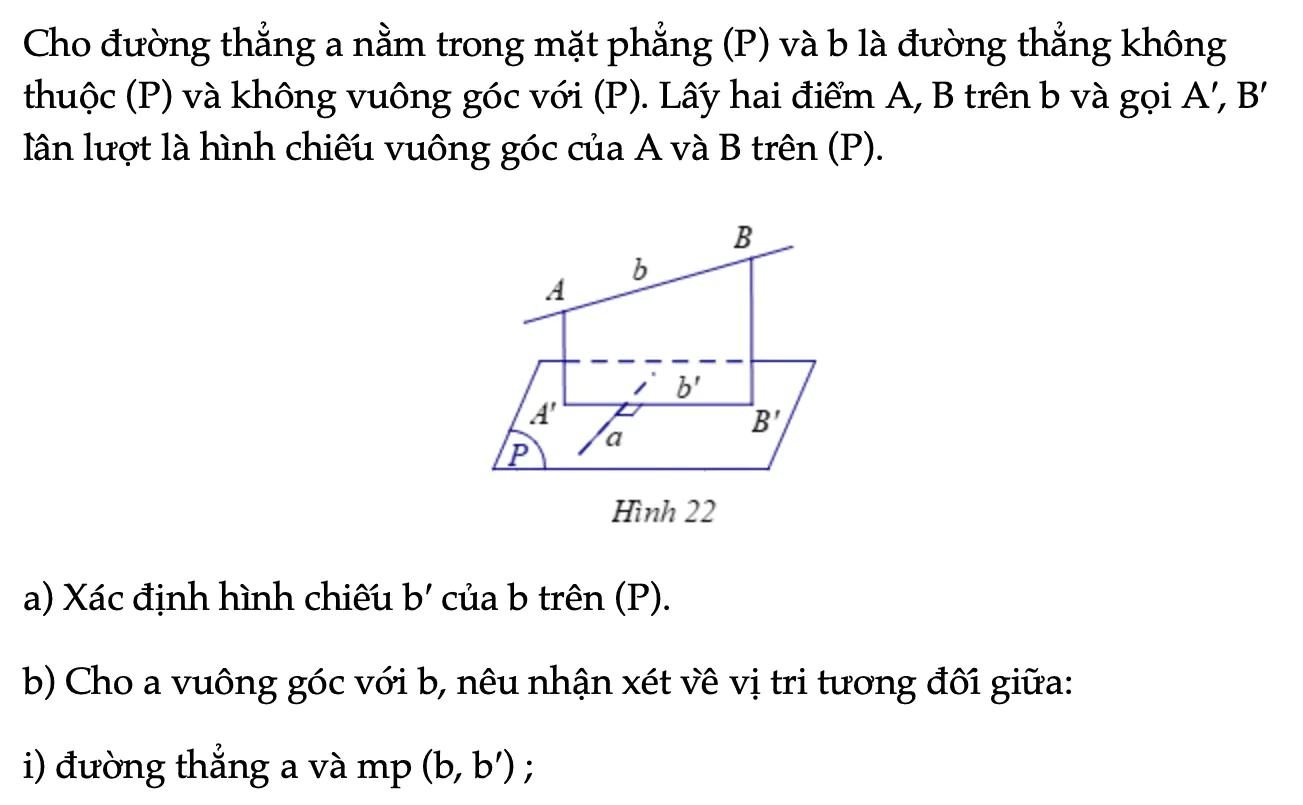
Hoạt động khám phá 6 trang 63 Toán 11 Tập 2
Cho đường thẳng a nằm trong mặt phẳng (P) và b là đường thẳng không thuộc (P) và không vuông góc với (P). Lấy hai điểm A, B trên b và gọi A′, B′ lần lượt là hình chiếu vuông góc của A và B trên (P).

Thực hành 5 trang 64 Toán 11 Tập 2
Cho tứ diện OABC có OA, OB, OC đôi một vuông góc. Vẽ đường thẳng qua O và vuông góc với (ABC) tại H. Chứng minh AH ⊥ BC.

Vận dụng 3 trang 64 Toán 11 Tập 2
Nêu cách tìm hình chiếu vuông góc của một đoạn thẳng AB trên trần nhà xuống nền nhà bằng hai dây dọi.
Giải bài tập Bài 3: Hai mặt phẳng vuông góc

Bài 1 trang 73 Toán 11 Tập 2
Cho hình chóp S.ABC có đáy là tam giác vuông tại C, mặt bên SAC là tam giác đều và nằm trong mặt phẳng vuông góc với (ABC). Bài 1 trang 73 Toán 11 Tập 2

Bài 2 trang 73 Toán 11 Tập 2
Cho tam giác đều ABC cạnh a, I trung điểm của BC, D là điểm đối xứng với A qua I. Bài 2 trang 73 Toán 11 Tập 2
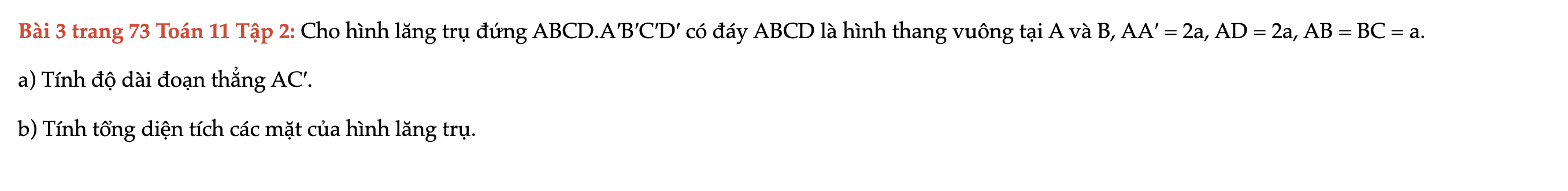
Bài 3 trang 73 Toán 11 Tập 2
Cho hình lăng trụ đứng ABCD.A′B′C′D′ có đáy ABCD là hình thang vuông tại A và B, AA′ = 2a, AD = 2a, AB = BC = a. Bài 3 trang 73 Toán 11 Tập 2

Bài 4 trang 74 Toán 11 Tập 2
Cho hình hộp ABCD.A′B′C′D′ có đáy là hình thoi. Cho biết AB = BD = a, A′C = 2a. Bài 4 trang 74 Toán 11 Tập 2
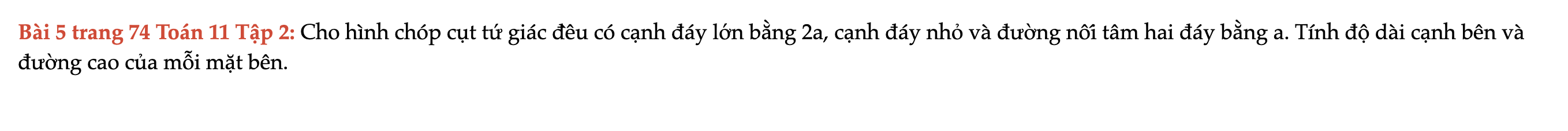
Bài 5 trang 74 Toán 11 Tập 2
Cho hình chóp cụt tứ giác đều có cạnh đáy lớn bằng 2a, cạnh đáy nhỏ và đường nối tâm hai đáy bằng a. Tính độ dài cạnh bên và đường cao của mỗi mặt bên. Bài 5 trang 74 Toán 11 Tập 2

Bài 6 trang 74 Toán 11 Tập 2
Kim tự tháp bằng kính tại bảo tàng Louvre ở Paris có dạng hình chóp tứ giác đều với chiều cao là 21,6 m và cạnh đáy dài 34 m. Tính độ dài cạnh bên và diện tích xung quanh của kim tự tháp. Bài 6 trang 74 Toán 11 Tập 2

Hoạt động khởi động trang 65 Toán 11 Tập 2
Trong thực tế, người ta thường nói mặt ngang và mặt đứng của các bậc thang vuông góc với nhau. Vậy thế nào là hai mặt phẳng vuông góc?
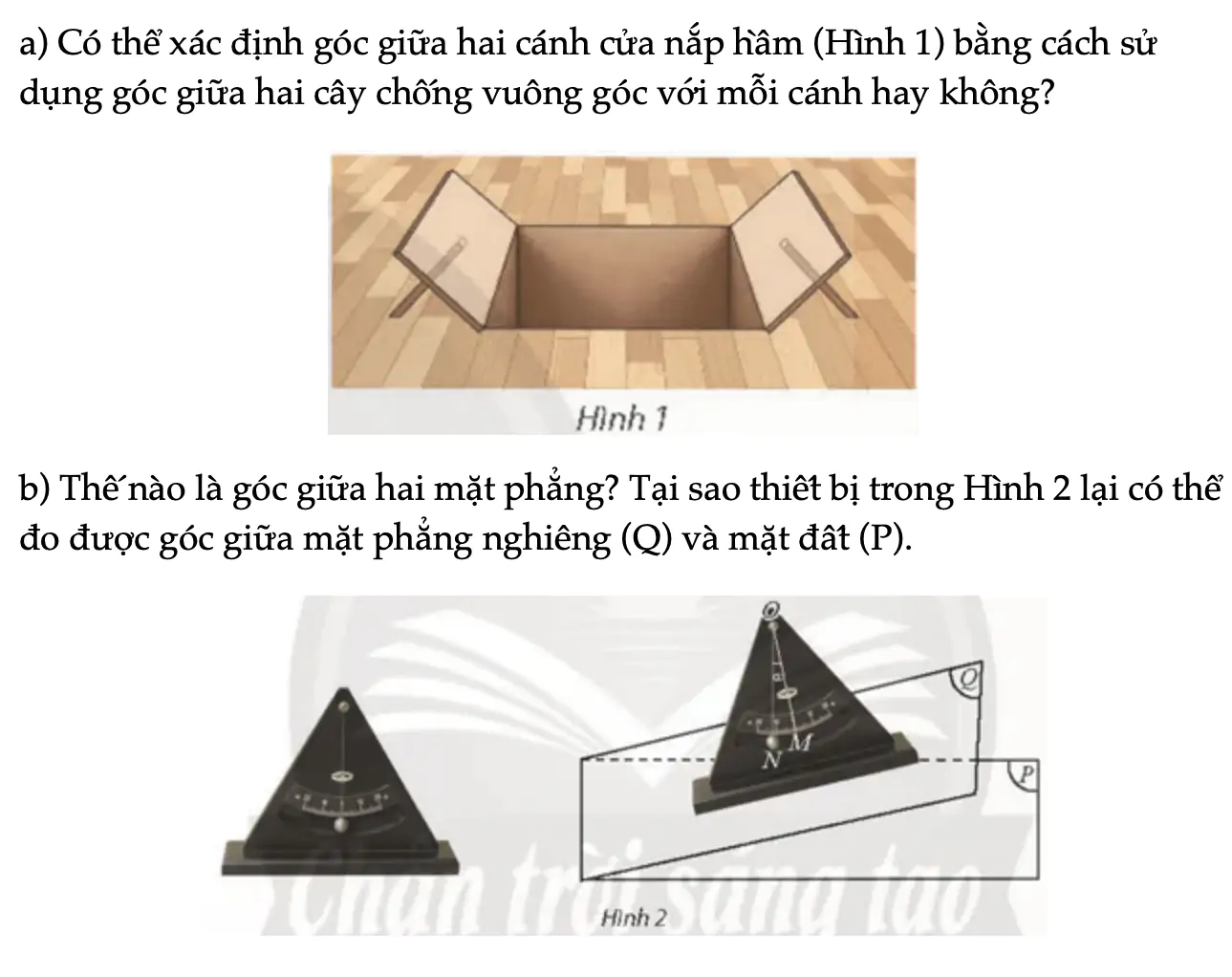
Hoạt động khám phá 1 trang 65 Toán 11 Tập 2
a) Có thể xác định góc giữa hai cánh cửa nắp hầm bằng cách sử dụng góc giữa hai cây chống vuông góc với mỗi cánh hay không? b) Thế nào là góc giữa hai mặt phẳng? Tại sao thiết bị trong Hình 2 lại có thể đo được góc giữa mặt phẳng nghiêng (Q) và (P).
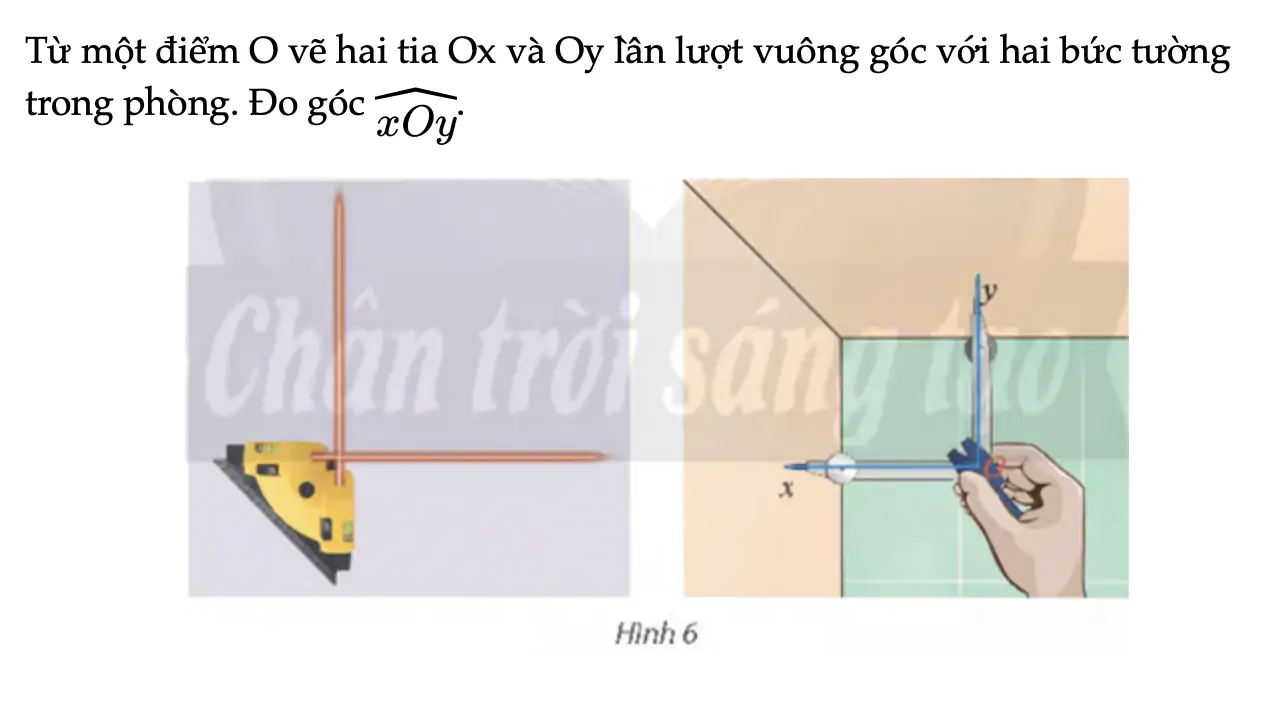
Hoạt động khám phá 2 trang 66 Toán 11 Tập 2
Từ một điểm O vẽ hai tia Ox và Oy lần lượt vuông góc với hai bức tường trong phòng. Đo góc xOy.
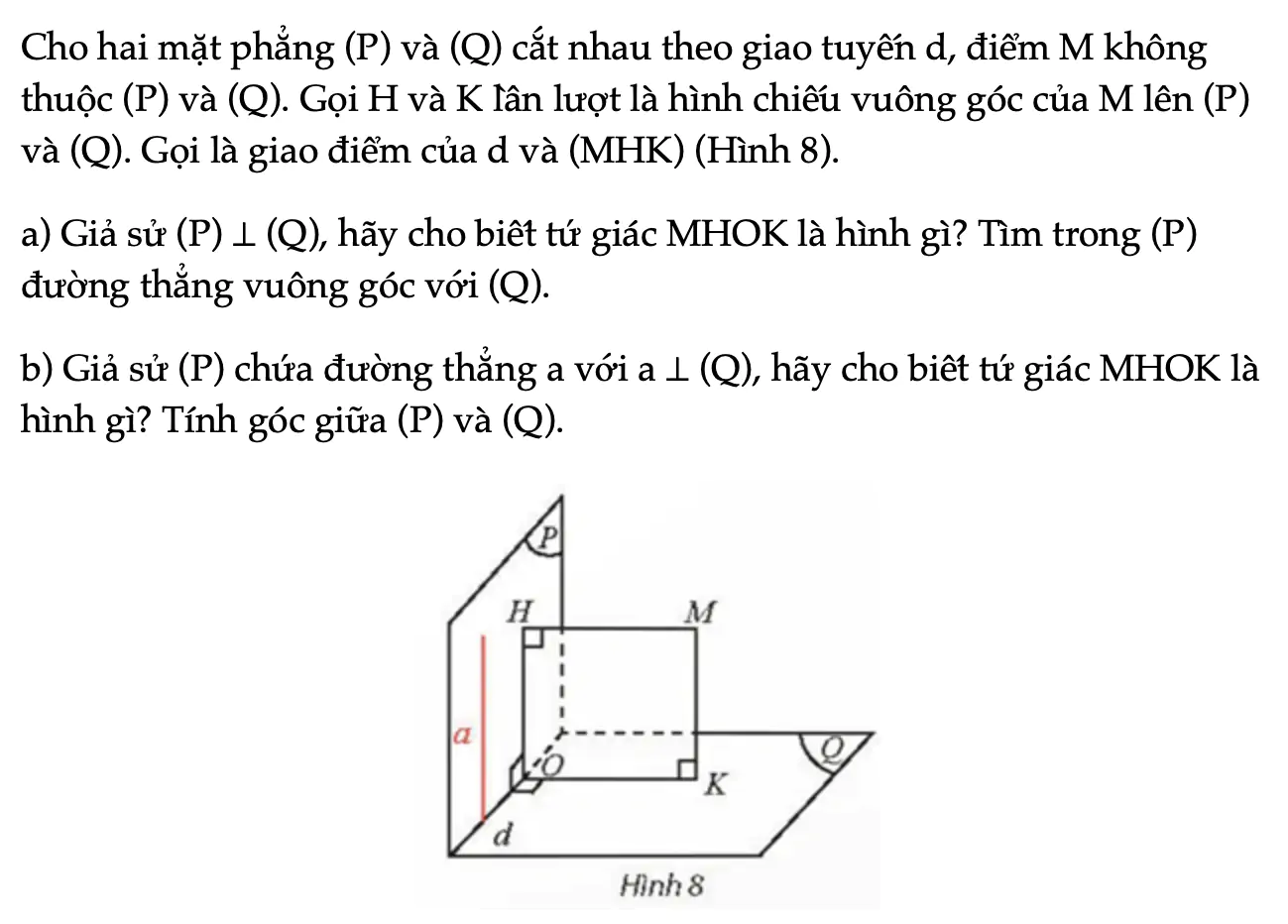
Hoạt động khám phá 3 trang 67 Toán 11 Tập 2
Cho hai mặt phẳng (P) và (Q) cắt nhau theo giao tuyến d, điểm M không thuộc (P) và (Q). Gọi H và K lần lượt là hình chiếu vuông góc của M lên (P) và (Q). Gọi là giao điểm của d và (MHK) (Hình 8).

Thực hành 1 trang 67 Toán 11 Tập 2
Cho hình chóp S.ABCD có các cạnh bên bằng nhau và đáy là hình vuông. Chứng minh rằng: a) (SAC) ⊥ (ABCD) . b) (SAC) ⊥ (SBD).

Vận dụng 1 trang 67 Toán 11 Tập 2
Mô tả cách kiểm tra một bức tường vuông góc với mặt sàn bằng hai cái êke trong Hình 10.
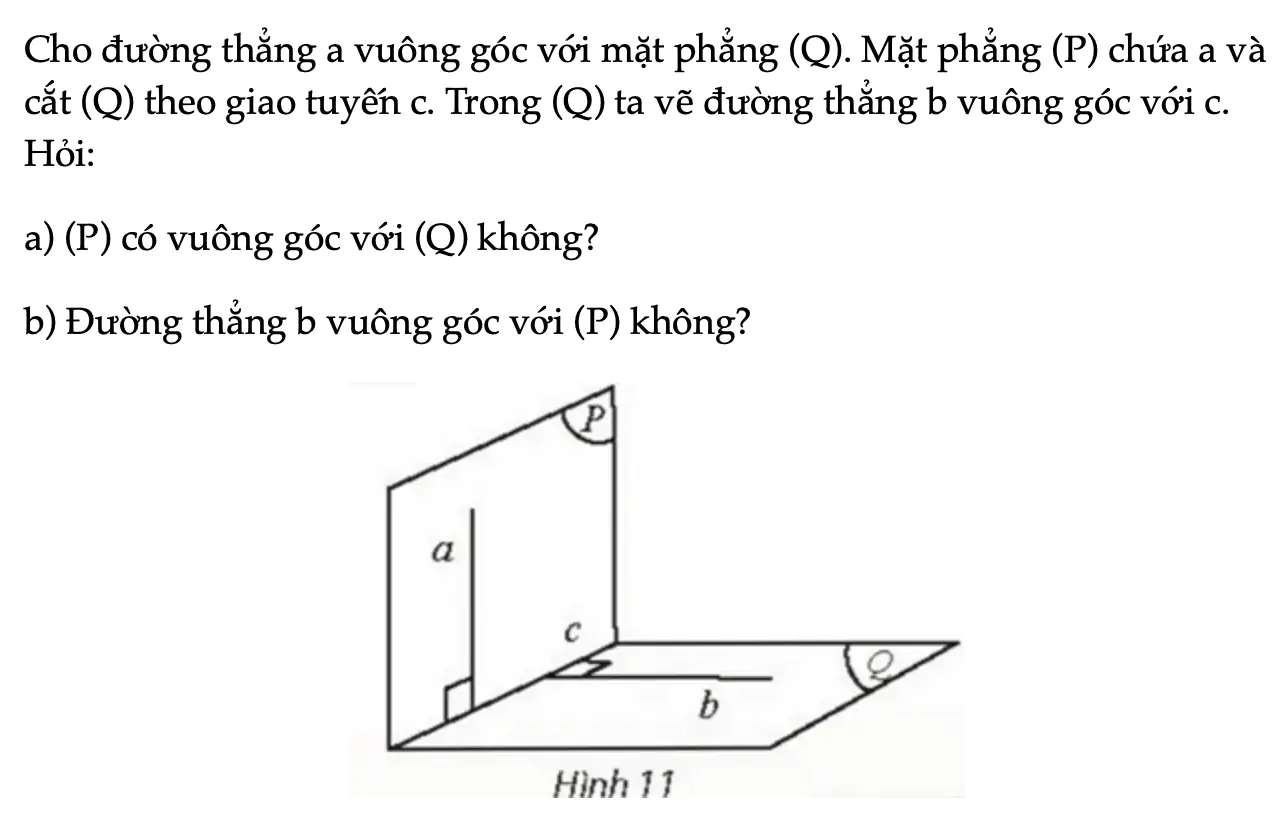
Hoạt động khám phá 4 trang 67 Toán 11 Tập 2
Cho đường thẳng a vuông góc với mặt phẳng (Q). Mặt phẳng (P) chứa a và cắt (Q) theo giao tuyến c. Trong (Q) ta vẽ đường thẳng b vuông góc với c. Hỏi: a) (P) có vuông góc với (Q) không? b) Đường thẳng b vuông góc với (P) không?
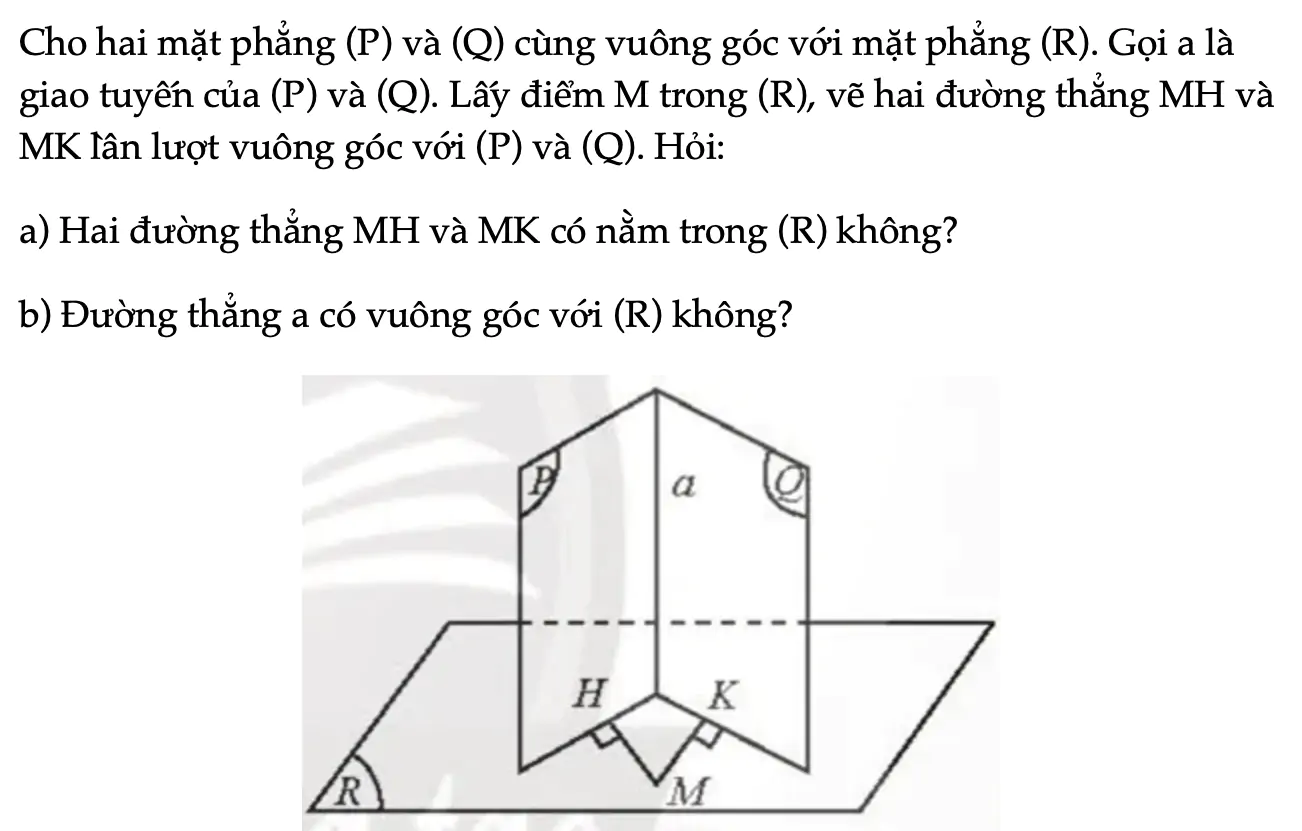
Hoạt động khám phá 5 trang 68 Toán 11 Tập 2
Cho hai mặt phẳng (P) và (Q) cùng vuông góc với mặt phẳng (R). Gọi a là giao tuyến của (P) và (Q). Lấy điểm M trong (R), vẽ hai đường thẳng MH và MK lần lượt vuông góc với (P) và (Q). Hỏi: a) Hai đường thẳng MH và MK có nằm trong (R) không?
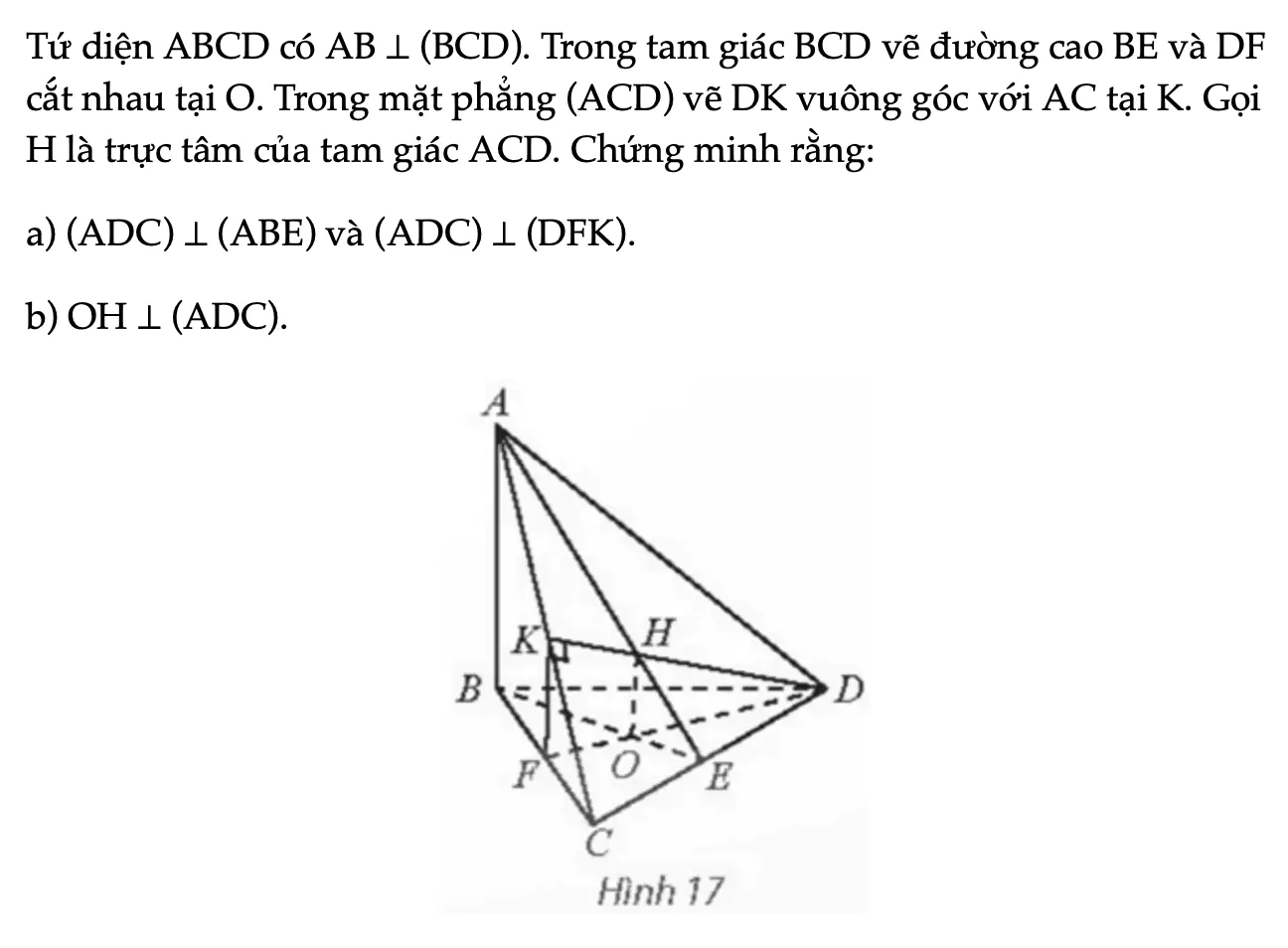
Thực hành 2 trang 69 Toán 11 Tập 2
Tứ diện ABCD có AB ⊥ (BCD). Trong tam giác BCD vẽ đường cao BE và DF cắt nhau tại O. Trong mặt phẳng (ACD) vẽ DK vuông góc với AC tại K. Gọi H là trực tâm của tam giác ACD. Chứng minh rằng: a) (ADC) ⊥ (ABE) và (ADC) ⊥ (DFK). b) OH ⊥ (ADC).

Vận dụng 2 trang 69 Toán 11 Tập 2
Nêu cách đặt một quyển sách lên mặt bàn sao cho tất cả các trang sách đều vuông góc với mặt bàn.

Hoạt động khám phá 6 trang 69 Toán 11 Tập 2
a) Cho hình lăng trụ ABCDE.A′B′C′D′E′ có cạnh bên AA′ vuông góc với một mặt phẳng đáy (Hình 18a). Có nhận xét gì về các mặt bên của hình lăng trụ này? b) Cho hình lăng trụ có đáy là đa giác đều và có cạnh bên vuông góc với một mặt phẳng đáy (Hình 18b).

Thực hành 3 trang 71 Toán 11 Tập 2
Cho hình lăng trụ lục giác đều ABCDEF.A′B′C′D′E′F′ có cạnh bên bằng h và cạnh đáy bằng a. Tính A′C và A′D theo a và h.

Vận dụng 3 trang 71 Toán 11 Tập 2
Một chiếc lồng đèn kéo quân có dạng hình lăng trụ lục giác đều với cạnh đáy bằng 10 cm và cạnh bên bằng 30 cm (Hình 20). Tính tổng diện tích các mặt bên của chiếc lồng đèn đó.
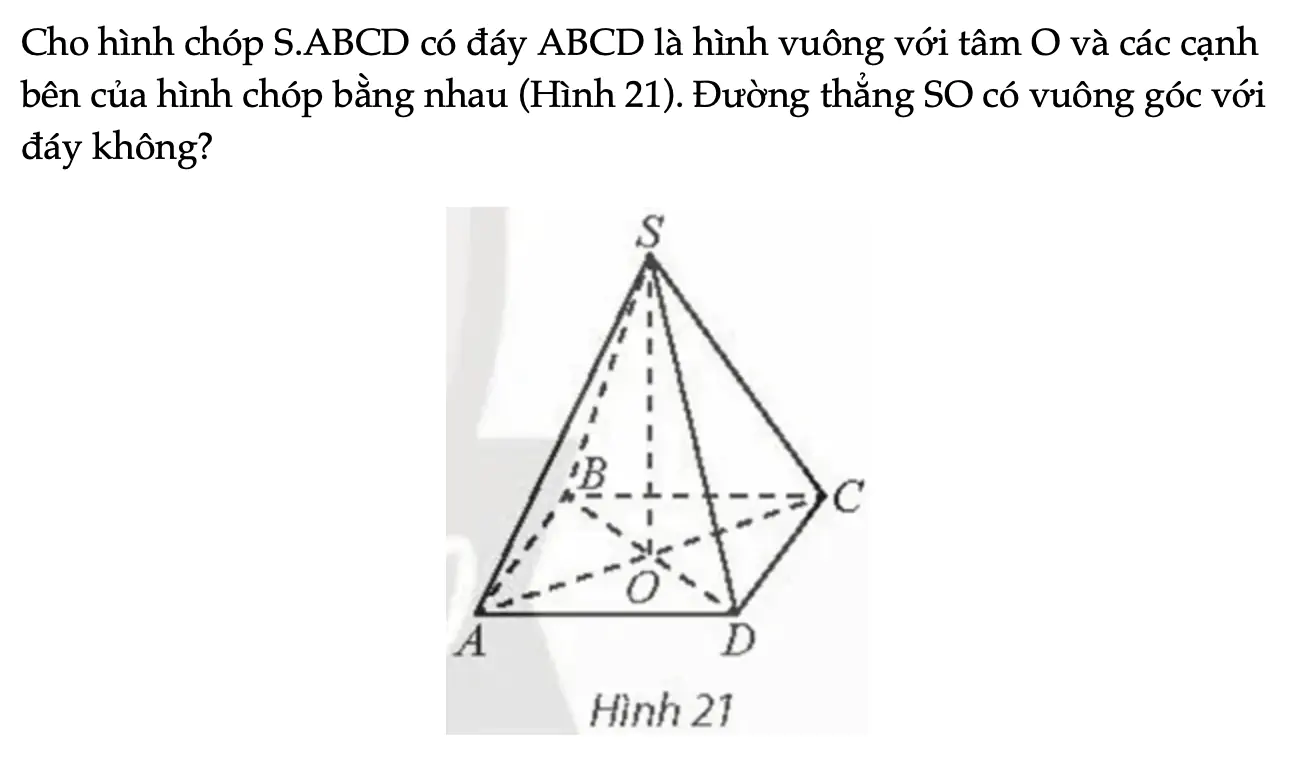
Hoạt động khám phá 7 trang 71 Toán 11 Tập 2
Cho hình chóp S.ABCD có đáy ABCD là hình vuông với tâm O và các cạnh bên của hình chóp bằng nhau (Hình 21). Đường thẳng SO có vuông góc với đáy không?

Thực hành 4 trang 72 Toán 11 Tập 2
Cho hình chóp tứ giác đều S.ABCD có O là tâm của đáy và AB = a, SA = 2a. Tính SO theo a.

Vận dụng 4 trang 72 Toán 11 Tập 2
Cho biết kim tự tháp Khafre tại Ai Cập có dạng hình chóp tứ giác đều với chiều cao khoảng 136m và cạnh đáy dài khoảng 152m. Tính độ dài đường cao của mặt bên xuất phát từ đỉnh của kim tự tháp.
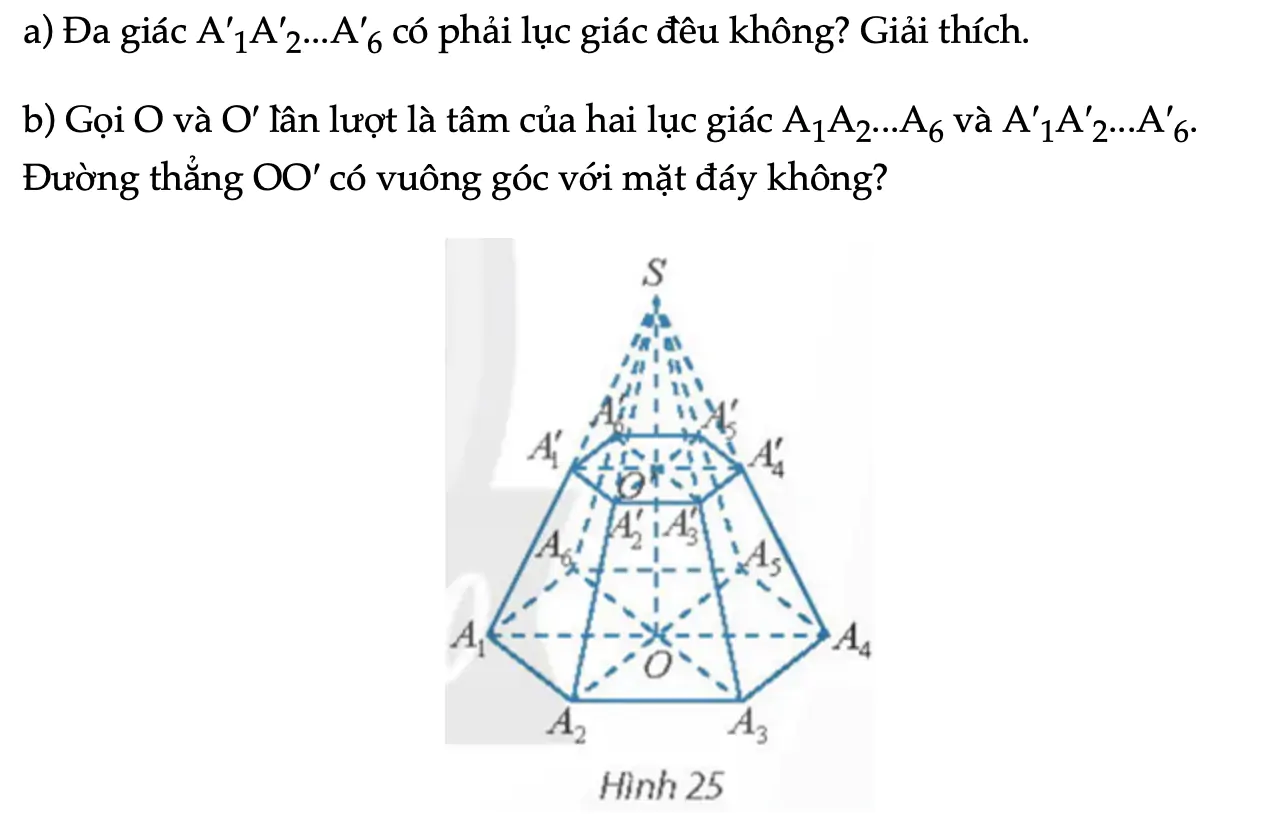
Hoạt động khám phá 8 trang 72 Toán 11 Tập 2
Cho hình chóp đều S.A1A2...A6. Mặt phẳng (P) song song với mặt đáy và cắt các cạnh bên lần lượt tại A′1A′2...A′6. a) Đa giác A′1A′2...A′6 có phái lục giác đều không? Giải thích. b) Đường thẳng OO′ có vuông góc với mặt đáy không?

Thực hành 5 trang 73 Toán 11 Tập 2
Cho hình chóp cụt tam giác đều ABC.A′B′C′ có cạnh đáy lớn bằng a, cạnh đáy nhỏ a/2 và cạnh bên 2a. Tính độ dài đường cao của hình chóp cụt đó.

Vận dụng 5 trang 73 Toán 11 Tập 2
Một người cần sơn tất cả các mặt của một cái bục để đặt tượng có dạng hình chóp cụt lục giác đều có cạnh đáy lớn 1 m, cạnh bên và cạnh đáy nhỏ bằng 0,7 m. Tính tổng diện tích cần sơn.
Giải bài tập Bài 4: Khoảng cách trong không gian

Bài 1 trang 81 Toán 11 Tập 2
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a có O là giao điểm của hai đường chéo. Bài 1 trang 81 Toán 11 Tập 2

Bài 2 trang 81 Toán 11 Tập 2
Cho hai tam giác cân ABC và ABD có đáy chung AB và không cùng nằm trong một mặt phẳng. Chứng minh rằng AB ⊥ CD. Bài 2 trang 81 Toán 11 Tập 2

Bài 3 trang 81 Toán 11 Tập 2
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA = SB = SC = SD = a căn 2. Gọi I, J lần lượt là trung điểm của AB và CD. Bài 3 trang 81 Toán 11 Tập 2
Bài 4 trang 81 Toán 11 Tập 2
Cho hình lăng trụ tam giác đều ABC.A′B′C′ có AB = a, góc giữa hai mặt phẳng (A′BC) và (ABC) bằng 60°. Tính khoảng cách giữa hai đáy của hình lăng trụ. Bài 4 trang 81 Toán 11 Tập 2

Bài 5 trang 81 Toán 11 Tập 2
Một cây cầu dành cho người đi bộ (Hình 22) có mặt sàn cầu cách mặt đường 3,5 m, khoảng cách từ đường thẳng a nằm trên tay vịn của cầu đến mặt sàn cầu là 0,8 m. Gọi b là đường thẳng kẻ theo tim đường. Bài 5 trang 81 Toán 11 Tập 2

Bài 6 trang 82 Toán 11 Tập 2
Cho hình hộp đứng ABCD.A′B′C′D′ có cạnh bên AA′ = 2a và đáy ABCD là hình thoi có AB = a và a căn 3. Bài 6 trang 82 Toán 11 Tập 2

Bài 7 trang 82 Toán 11 Tập 2
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh đều bằng a và có O là giao điểm hai đường chéo của đáy. Tính khoảng cách giữa hai đường thẳng AC và SB. Bài 7 trang 82 Toán 11 Tập 2
Bài 8 trang 82 Toán 11 Tập 2
Tính thể tích của khối chóp cụt lục giác đều ABCDEF.A′B′C′D′E′F′ với O và O′ là tâm hai đáy, cạnh đáy lớn và đáy nhỏ lần lượt là a và a/2; OO' = a. Bài 8 trang 82 Toán 11 Tập 2

Hoạt động khởi động trang 74 Toán 11 Tập 2
Có bao nhiêu loại khoảng cách trong công trình đang xây dụng này? Làm thế nào để tính được những khoảng cách đó?
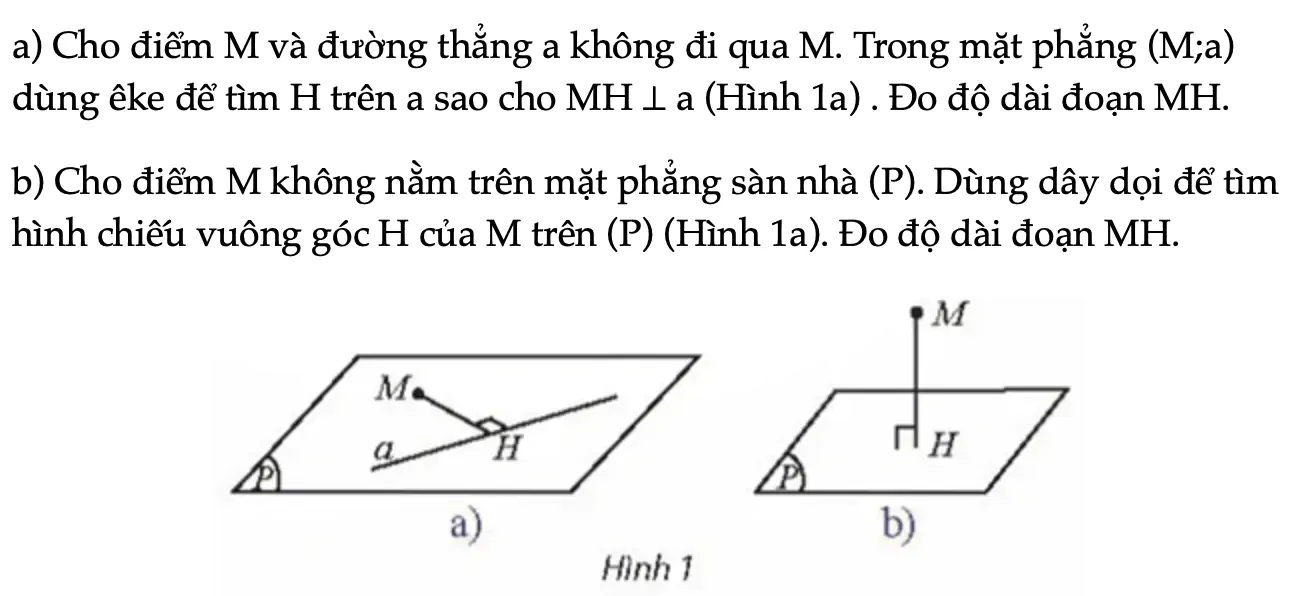
Hoạt động khám phá 1 trang 74 Toán 11 Tập 2
a) Cho điểm M và đường thẳng a không đi qua M. Trong mặt phẳng (M;a) dùng êke để tìm H trên a sao cho MH ⊥ a (Hình 1a) . Đo độ dài đoạn MH. b) Cho điểm M không nằm trên mặt phẳng sàn nhà (P). Dùng dây dọi để tìm hình chiếu vuông góc H của M trên (P)

Thực hành 1 trang 75 Toán 11 Tập 2
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Biết SA = a và SA ⊥ (ABCD). Cho biết OA = a. a) Tính khoảng cách từ B đến (SAD). b) Tính khoảng cách từ A đến đường thẳng SC.
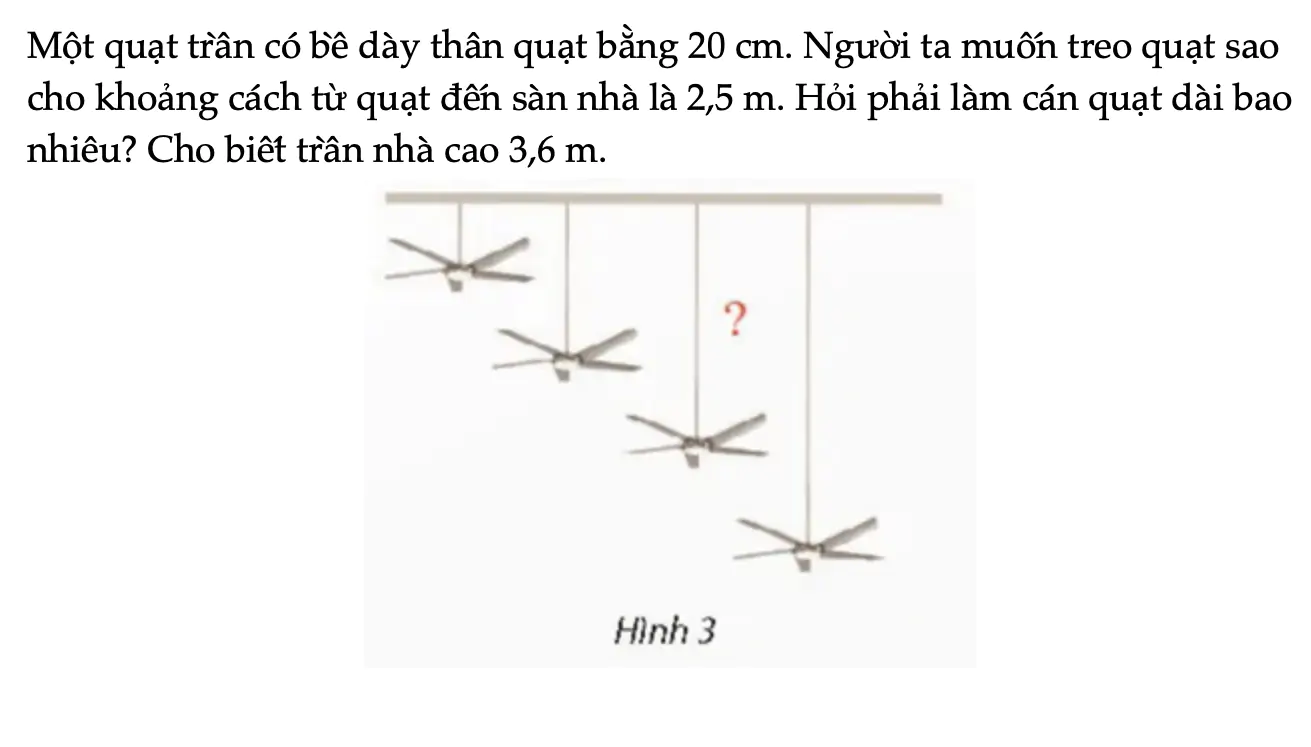
Vận dụng 1 trang 75 Toán 11 Tập 2
Một quạt trần có bề dày thân quạt bằng 20 cm. Người ta muốn treo quạt sao cho khoảng cách từ quạt đến sàn nhà là 2,5 m. Hỏi phải làm cán quạt dài bao nhiêu? Cho biết trần nhà cao 3,6 m.
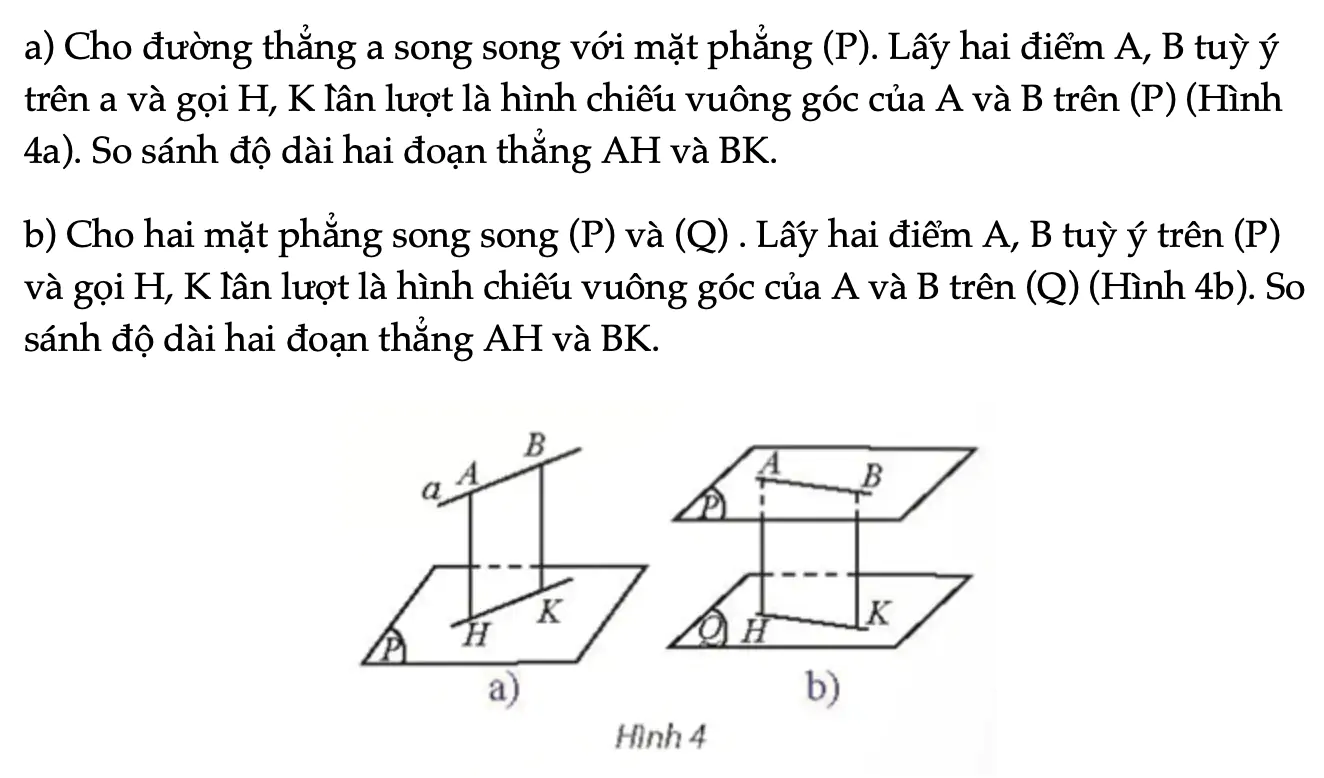
Hoạt động khám phá 2 trang 76 Toán 11 Tập 2
a) Cho đường thẳng a song song với mặt phẳng (P). Lấy hai điểm A, B tuỳ ý trên a và gọi H, K lần lượt là hình chiếu vuông góc của A và B trên (P) (Hình 4a). So sánh độ dài hai đoạn thẳng AH và BK.

Thực hành 2 trang 77 Toán 11 Tập 2
ho hình lập phương ABCD.A′B′C′D′ có cạnh bằng a. Tính khoảng cách: a) Giữa hai mặt phẳng (ACD′) và (A′C′B); b) Giữa đường thẳng AB và (A′B′C′D′).
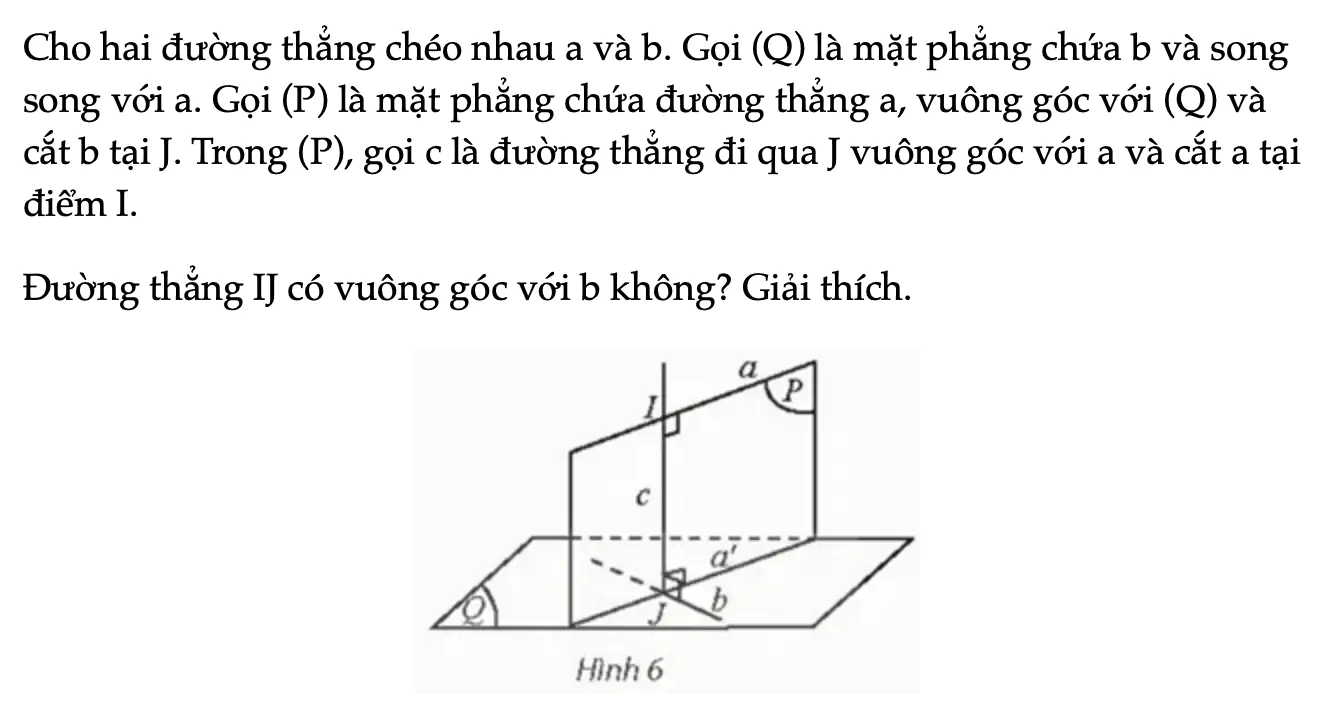
Hoạt động khám phá 3 trang 77 Toán 11 Tập 2
Cho hai đường thẳng chéo nhau a và b. Gọi (Q) là mặt phẳng chứa b và song song với a. Gọi (P) là mặt phẳng chứa đường thẳng a, vuông góc với (Q) và cắt b tại J. Trong (P), gọi c là đường thẳng đi qua J vuông góc với a và cắt a tại điểm I.

Thực hành 3 trang 78 Toán 11 Tập 2
Cho tứ diện OABC có ba cạnh OA, OB, OC đều bằng a và vuông góc từng đôi một. Tính khoảng cách giữa hai đường thẳng: a) OA và BC; b) OB và AC.

Vận dụng 2 trang 78 Toán 11 Tập 2
Một căn phòng có trần cao 3,2 m. Tính khoảng cách giữa một đường thẳng a trên trần nhà và đường thẳng b trên sàn nhà.
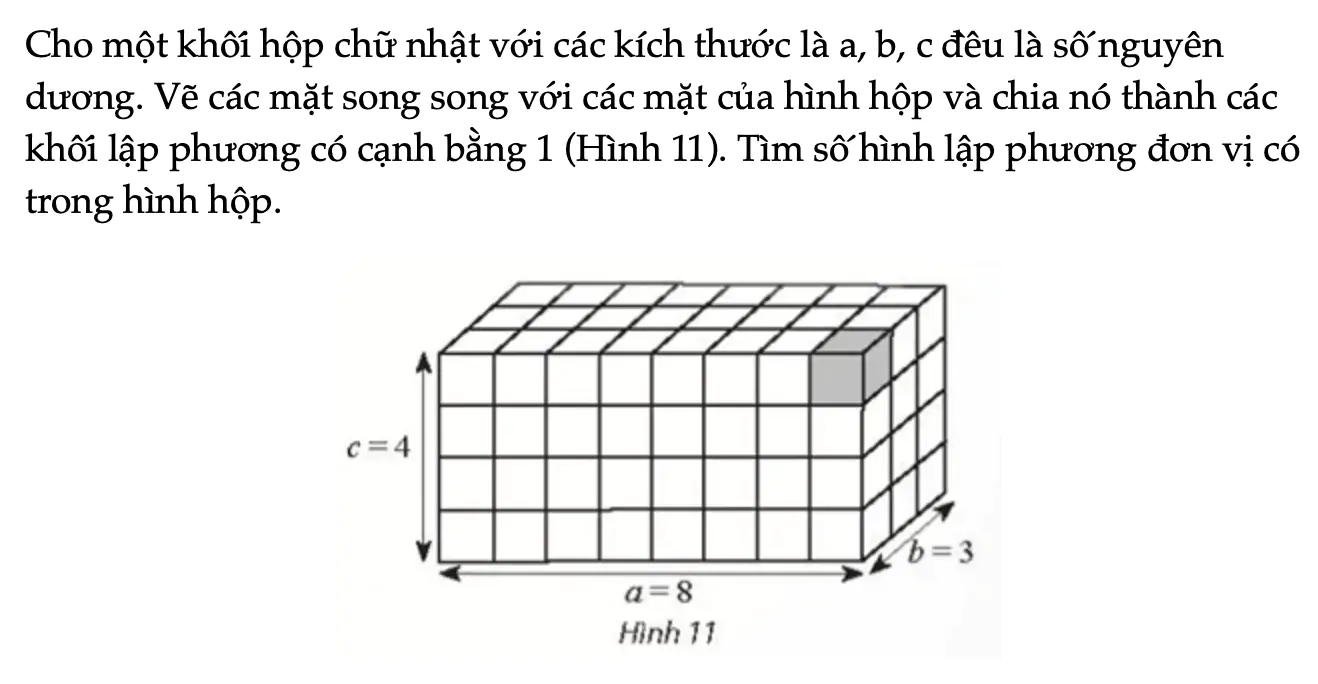
Hoạt động khám phá 4 trang 78 Toán 11 Tập 2
Cho một khối hộp chữ nhật với các kích thước là a, b, c đều là số nguyên dương. Vẽ các mặt song song với các mặt của hình hộp và chia nó thành các khối lập phương có cạnh bằng 1 (Hình 11). Tìm số hình lập phương đơn vị có trong hình hộp.
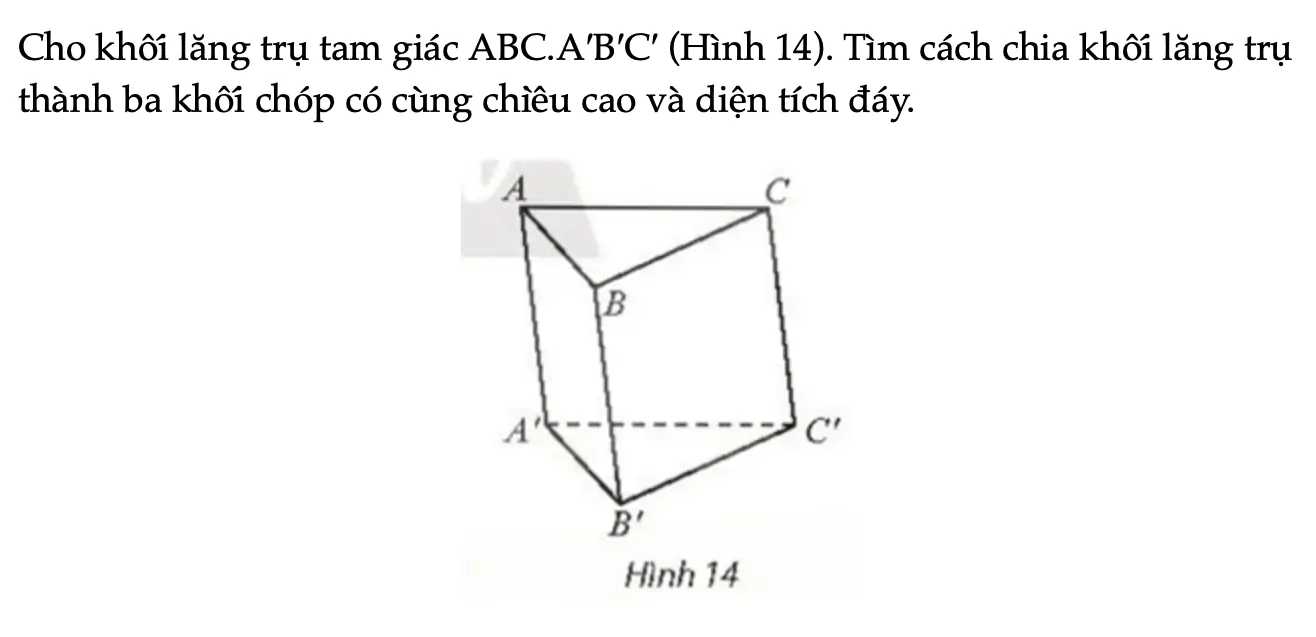
Hoạt động khám phá 5 trang 79 Toán 11 Tập 2
Cho khối lăng trụ tam giác ABC.A′B′C′ (Hình 14). Tìm cách chia khối lăng trụ thành ba khối chóp có cùng chiều cao và diện tích đáy.
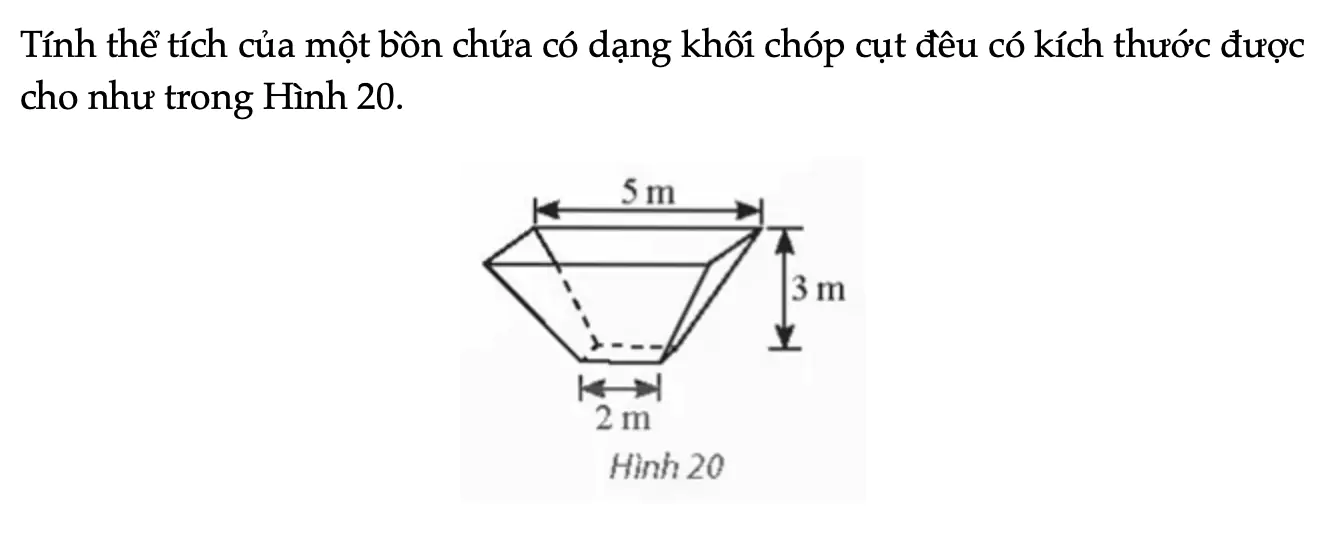
Thực hành 4 trang 81 Toán 11 Tập 2
Tính thể tích của một bồn chứa có dạng khối chóp cụt đều có kích thước được cho như trong Hình 20.
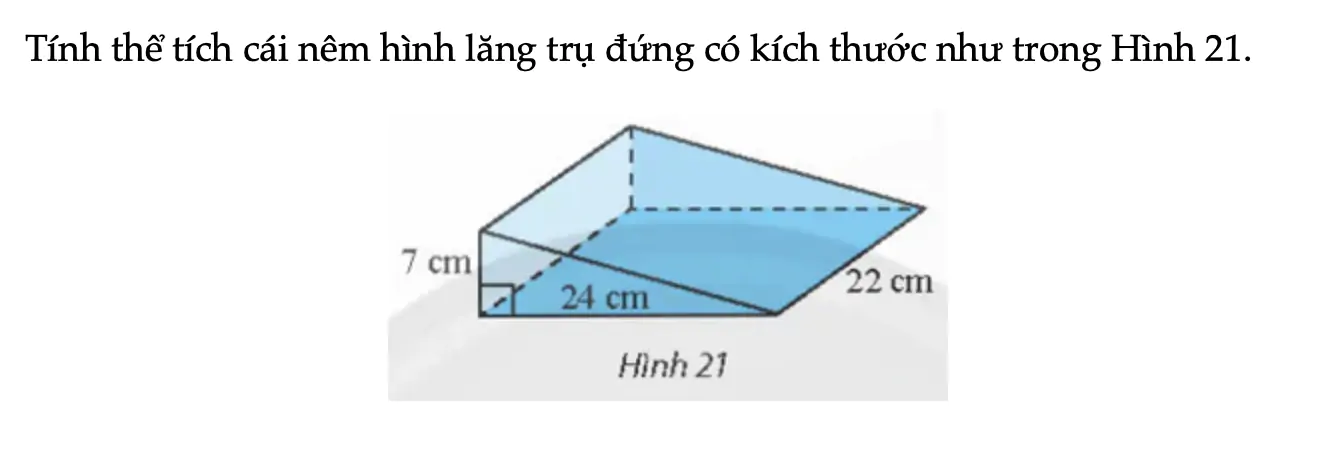
Vận dụng 3 trang 81 Toán 11 Tập 2
Tính thể tích cái nêm hình lăng trụ đứng có kích thước như trong Hình 21.
Giải bài tập Bài 5: Góc giữa đường thẳng và mặt phẳng. Góc nhị diện

Bài 1 trang 85 Toán 11 Tập 2
Cho tứ diện đều ABCD. Vẽ hình bình hành BCED. Tìm góc giữa đường thẳng AB và (BCD). Bài 1 trang 85 Toán 11 Tập 2

Bài 2 trang 85 Toán 11 Tập 2
Cho hình chóp tứ giác đều S.ABCD có O là tâm của đáy và có tất cả các cạnh bằng nhau. Tìm góc giữa đường thẳng SA và (ABCD). Bài 2 trang 85 Toán 11 Tập 2

Bài 3 trang 85 Toán 11 Tập 2
Cho hình chóp cụt lục giác đều ABCDEF.A′B′C′D′E′F′ với O và O′ là tâm hai đáy, cạnh đáy lớn và đáy nhỏ lần lượt là a và a/2; OO' = a. Tìm góc giữa cạnh bên và mặt đáy. Bài 3 trang 85 Toán 11 Tập 2

Bài 4 trang 85 Toán 11 Tập 2
Một con dốc có dạng hình lăng trụ đứng tam giác với kích thước như trong Hình 9. Tính số đo góc giữa đường thẳng CA′ và (CC′B′B). Bài 4 trang 85 Toán 11 Tập 2

Bài 5 trang 85 Toán 11 Tập 2
Người ta định đào một cái hầm có dạng hình chóp cụt tứ giác đều có hai cạnh đáy là 14 m và 10 m. Mặt bên tạo với đáy nhỏ thành một góc nhị diện có số đo bằng 135°. Tính số mét khối đất cần phải di chuyển ra khỏi hầm. Bài 5 trang 85 Toán 11 Tập 2
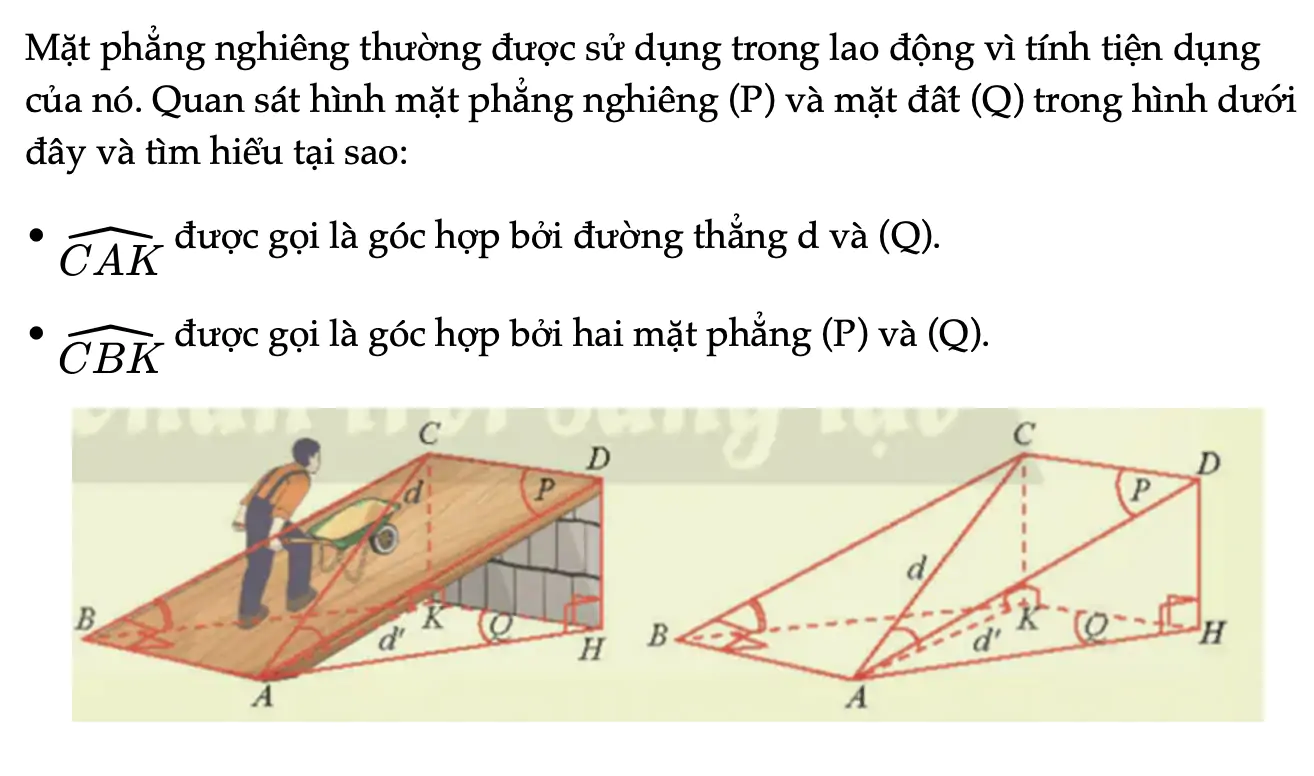
Hoạt động khởi động trang 82 Toán 11 Tập 2
Mặt phẳng nghiêng thường được sử dụng trong lao động vì tính tiện dụng của nó. Quan sát hình mặt phẳng nghiêng (P) và mặt đất (Q) trong hình dưới đây và tìm hiểu tại sao.
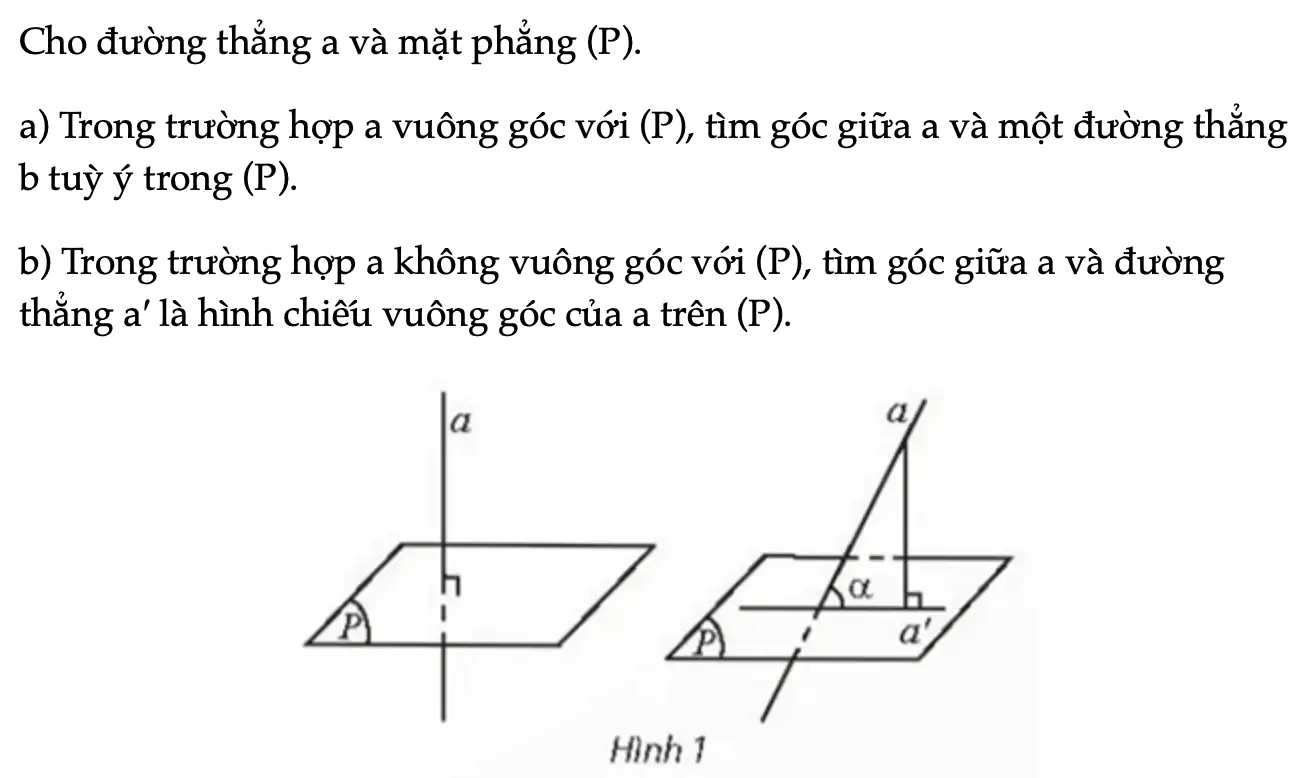
Hoạt động khám phá 1 trang 82 Toán 11 Tập 2
Cho đường thẳng a và mặt phẳng (P). a) Trong trường hợp a vuông góc với (P), tìm góc giữa a và một đường thẳng b tuỳ ý trong (P). b) Trong trường hợp a không vuông góc với (P), tìm góc giữa a và đường thẳng a′ là hình chiếu vuông góc của a trên (P).

Thực hành 1 trang 83 Toán 11 Tập 2
Cho hình lập phương ABCD.A′B′C′D′. Tính góc giữa các đường thẳng sau đây với mặt phẳng (ABCD): a) AA′ ; b) BC′ ; c) A′C.
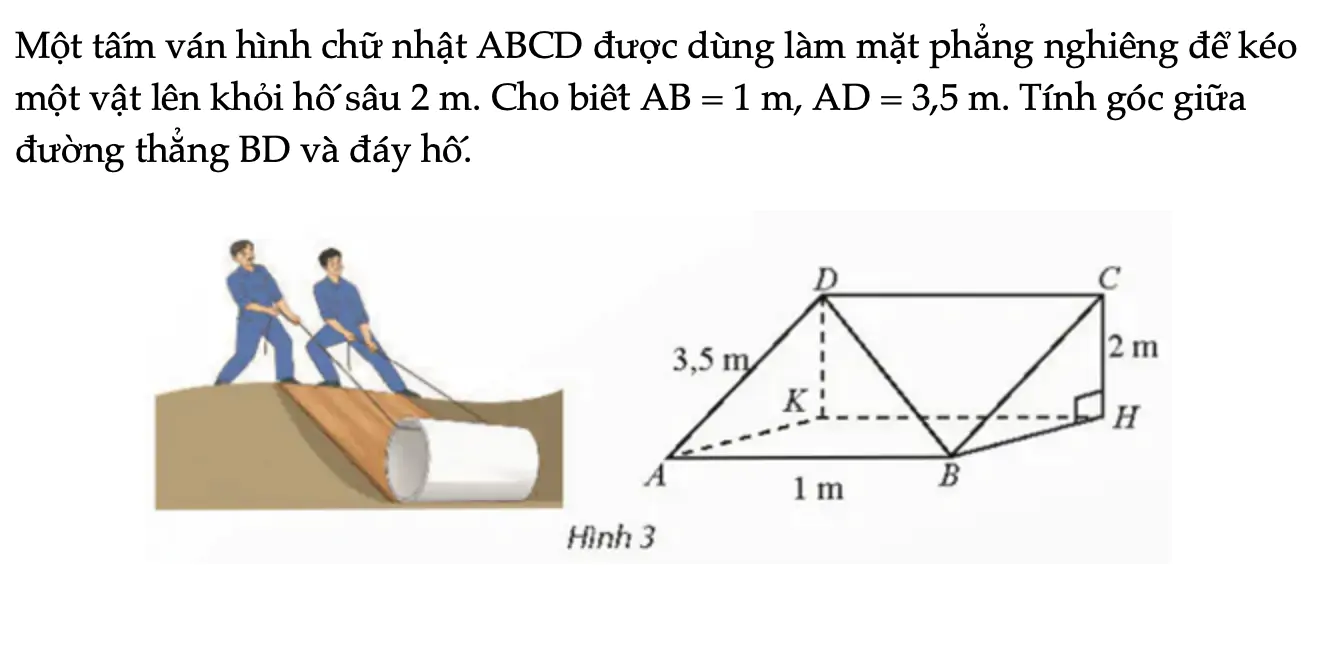
Vận dụng 1 trang 83 Toán 11 Tập 2
Một tấm ván hình chữ nhật ABCD được dùng làm mặt phẳng nghiêng để kéo một vật lên khỏi hố sâu 2 m. Cho biết AB = 1 m, AD = 3,5 m. Tính góc giữa đường thẳng BD và đáy hố.
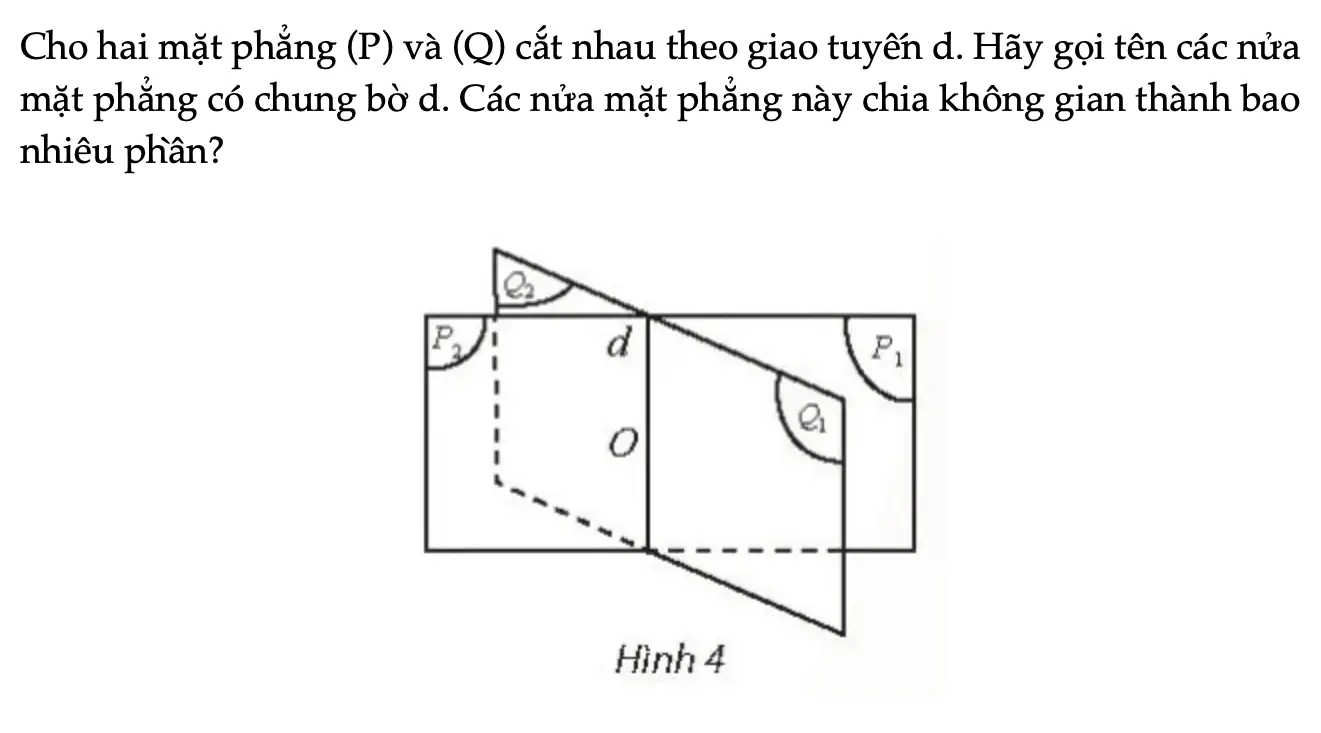
Hoạt động khám phá 2 trang 84 Toán 11 Tập 2
Cho hai mặt phẳng (P) và (Q) cắt nhau theo giao tuyến d. Hãy gọi tên các nửa mặt phẳng có chung bờ d. Các nửa mặt phẳng này chia không gian thành bao nhiêu phần
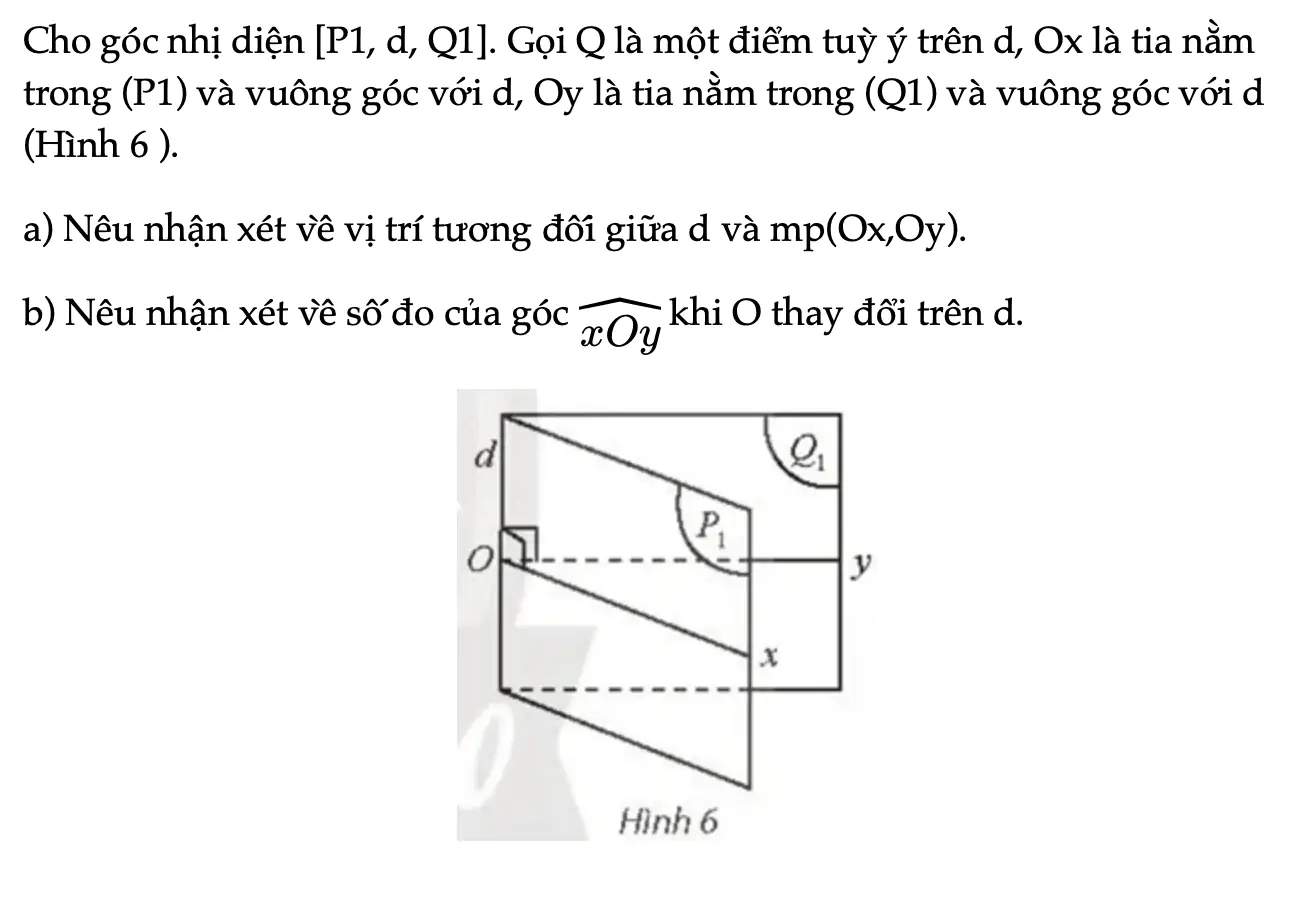
Hoạt động khám phá 3 trang 84 Toán 11 Tập 2
Cho góc nhị diện [P1, d, Q1]. Gọi Q là một điểm tuỳ ý trên d, Ox là tia nằm trong (P1) và vuông góc với d, Oy là tia nằm trong (Q1) và vuông góc với d (Hình 6 ).

Thực hành 2 trang 85 Toán 11 Tập 2
Cho hình chóp tứ giác đều S.ABCD với O là tâm của đáy và có tất cả các cạnh đều bằng a. Xác định và tính góc phẳng nhị diện: a) [S, BC, O]; b) [C, SO, B].

Vận dụng 2 trang 85 Toán 11 Tập 2
Cho biết kim tự tháp Memphis tại bang Tennessee (Mỹ) có dạng hình chóp tứ giác đều với chiều cao 98m và cạnh đáy 180m. Tính số đo góc nhị diện tạo bởi mặt bên và mặt đáy.
Giải bài tập Bài tập cuối chương 8

Bài 1 trang 86 Toán 11 Tập 2
Cho hình chóp S.ABCD có đáy ABCD là hình vuông, SA vuông góc với mặt đáy. Đường thẳng CD vuông góc với mặt phẳng nào sau đây. Bài 1 trang 86 Toán 11 Tập 2

Bài 2 trang 86 Toán 11 Tập 2
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh b, SA vuông góc với mặt đáy, SC = 2b căn 2. Số đo góc giữa cạnh bên SC và mặt đáy là. Bài 2 trang 86 Toán 11 Tập 2

Bài 3 trang 86 Toán 11 Tập 2
Cho hình chóp S.ABCD có các cạnh bên và cạnh đáy đều bằng a. Gọi M là trung điểm của SA. Mặt phẳng (MBD) vuông góc với mặt phẳng nào dưới đây. Bài 3 trang 86 Toán 11 Tập 2

Bài 4 trang 86 Toán 11 Tập 2
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng và chiều cao bằng a căn 2. Khoảng cách từ tâm O của đáy ABC đến một mặt bên là. Bài 4 trang 86 Toán 11 Tập 2

Bài 5 trang 86 Toán 11 Tập 2
Thể tích của khối chóp cụt tam giác đều có cạnh đáy lớn bằng 2a, cạnh đáy nhỏ bằng a và chiều cao bằng (a căn 6)/3 là. Bài 5 trang 86 Toán 11 Tập 2

Bài 6 trang 86 Toán 11 Tập 2
Cho chóp tứ giác S.ABCD có đáy là hình chữ nhật với AB = 4a, AD = 3a. Các cạnh bên đều có độ dài 5a. Góc nhị diện [S, BC, A] có số đo là. Bài 6 trang 86 Toán 11 Tập 2

Bài 7 trang 86 Toán 11 Tập 2
Nếu hình hộp chữ nhật có ba kích thước là 3, 4, 5 thì độ dài đường chéo của nó là. Bài 7 trang 86 Toán 11 Tập 2

Bài 8 trang 86 Toán 11 Tập 2
Thể tích của khối lăng trụ tam giác đều có tất cả các cạnh đều bằng a là. Bài 8 trang 86 Toán 11 Tập 2
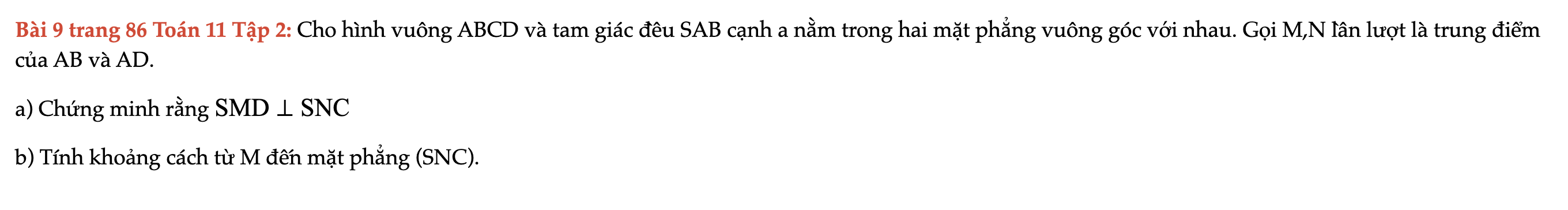
Bài 9 trang 86 Toán 11 Tập 2
Cho hình vuông ABCD và tam giác đều SAB cạnh a nằm trong hai mặt phẳng vuông góc với nhau. Gọi M,N lần lượt là trung điểm của AB và AD. Bài 9 trang 86 Toán 11 Tập 2

Bài 10 trang 87 Toán 11 Tập 2
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA ⊥ (ABCD) và SA = a. Gọi M, N, P lần lượt là trung điểm của SB, SC và SD. Tính khoảng cách giữa AM và NP. Bài 10 trang 87 Toán 11 Tập 2

Bài 11 trang 87 Toán 11 Tập 2
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D, AB = AD = 2a, CD = a; số đo góc nhị diện [S, BC, A] bằng 60°. Gọi I là trung điểm của cạnh AD. Bài 11 trang 87 Toán 11 Tập 2

Bài 12 trang 87 Toán 11 Tập 2
Một chân cột bằng gang có dạng hình chóp cụt tứ giác đều có cạnh đáy lớn bằng 2a, cạnh đáy nhỏ bằng a, chiều cao h = 2a và bán kính đáy phần trụ rỗng bên trong bằng a/2. Bài 12 trang 87 Toán 11 Tập 2
Bài 13 trang 87 Toán 11 Tập 2
Cho hình hộp ABCD.A′B′C′D′ có cạnh bên AA′ = a, đáy ABCD là hình thoi có AB = BD = a. Hình chiếu vuông góc của A′ lên mặt đáy trùng với điểm O là giao điểm hai đường chéo của đáy. Tính thể tích của khối hộp. Bài 13 trang 87 Toán 11 Tập 2