Giải bài tập Toán 11 Chương 3: Giới hạn. Hàm số liên tục | Chân trời sáng tạo
Hướng dẫn giải chi tiết Chương 3: Giới hạn. Hàm số liên tục
Giải bài tập Bài 1: Giới hạn của dãy số

Bài 1 trang 69 Toán 11 Tập 1
Tìm các giới hạn sau. Bài 1 trang 69 Toán 11 Tập 1

Bài 2 trang 69 Toán 11 Tập 1
Tính tổng của các cấp số nhân lùi vô hạn sau. Bài 2 trang 69 Toán 11 Tập 1

Bài 3 trang 69 Toán 11 Tập 1
Viết số thập phân vô hạn tuần hoàn 0,444 ... dưới dạng phân số. Bài 3 trang 69 Toán 11 Tập 1

Bài 4 trang 70 Toán 11 Tập 1
Từ hình vuông đầu tiên có cạnh bằng 1 (đơn vị độ dài), nối các trung điểm của bốn cạnh để có hình vuông thứ hai. Tiếp tục nối các trung điểm của bốn cạnh của hình vuông thứ hai để được hình vuông thứ ba. Bài 4 trang 70 Toán 11 Tập 1
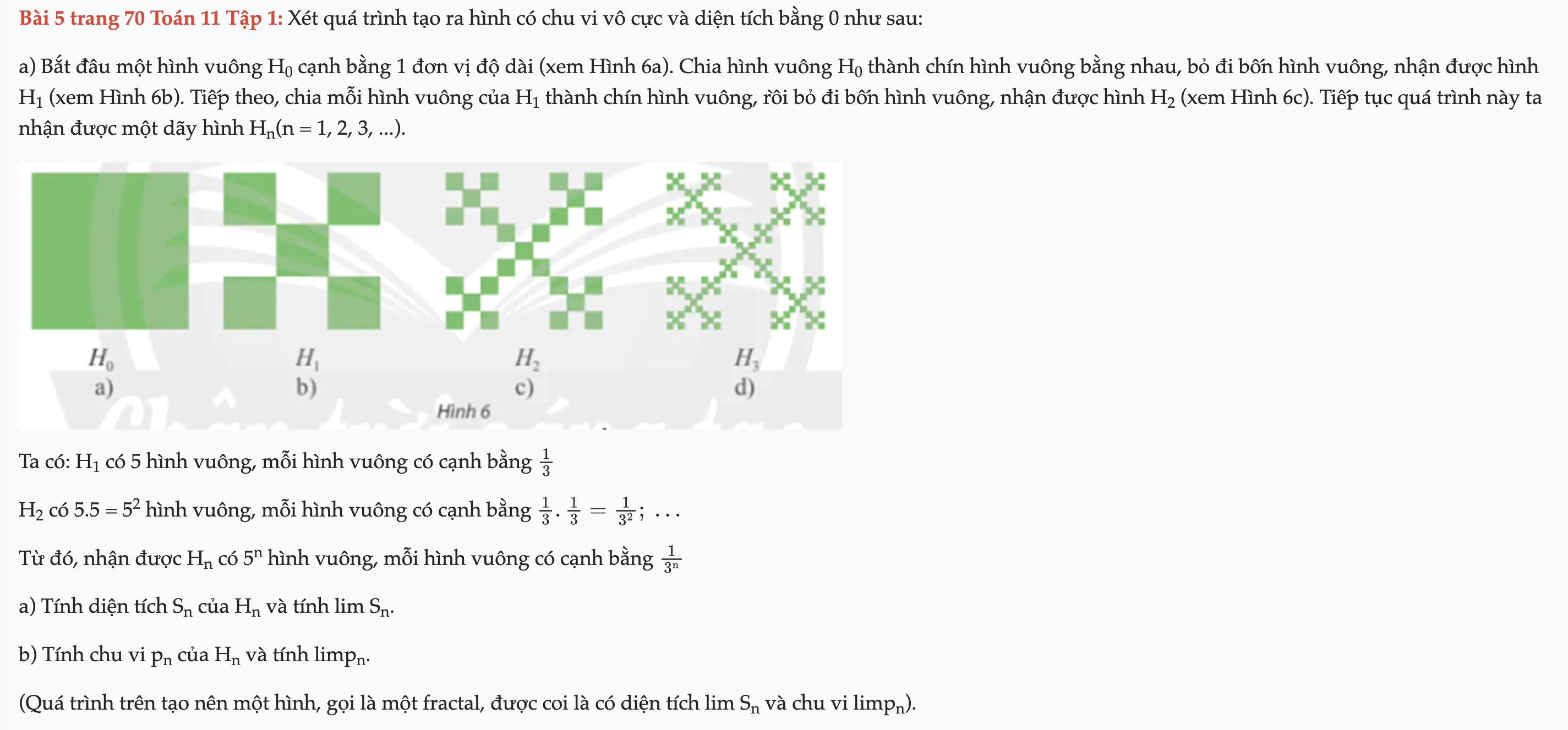
Bài 5 trang 70 Toán 11 Tập 1
Bài 5 trang 70 Toán 11 Tập 1

Hoạt động khám phá 1 trang 64 Toán 11 Tập 1
Cho dãy số (un). a) Tìm các giá trị còn thiếu trong bảng sau: b) Với n như thế nào thì |un| bé hơn 0,01; 0,001? c) Một số số hạng của dãy số được biểu diễn trên trục số như Hình 1.
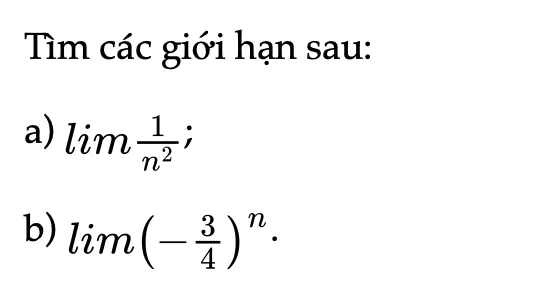
Thực hành 1 trang 65 Toán 11 Tập 1
Tìm các giới hạn sau.

Hoạt động khám phá 2 trang 65 Toán 11 Tập 1
Cho dãy số (un). a) Cho dãy số (vn) với vn = un – 2. Tìm giới hạn lim vn. b) Biểu diễn các điểm u1, u2, u3, u4 trên trục số. Có nhận xét gì về vị trí của các điểm un khi n trở nên rất lớn?

Thực hành 2 trang 65 Toán 11 Tập 1
Tìm các giới hạn sau.
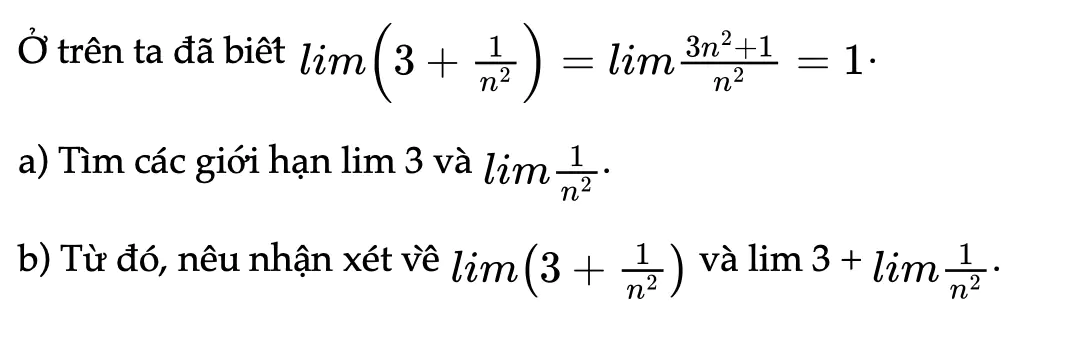
Hoạt động khám phá 3 trang 66 Toán 11 Tập 1
Thực hiện các yêu cầu bài toán.

Thực hành 3 trang 66 Toán 11 Tập 1
Tìm các giới hạn sau.

Hoạt động khám phá 4 trang 67 Toán 11 Tập 1
Từ một hình vuông có cạnh bằng 1, tô màu một nửa hình vuông, rồi tô màu một nửa hình còn lại, và cứ tiếp tục như vậy (xem Hình 2).
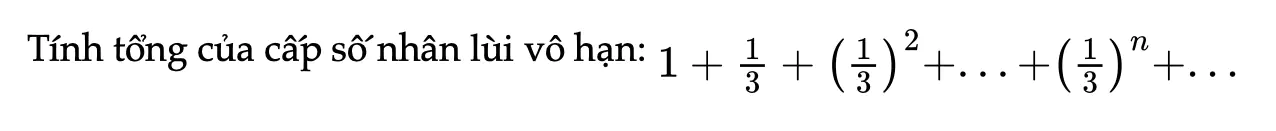
Thực hành 4 trang 68 Toán 11 Tập 1
Tính tổng của cấp số nhân lùi vô hạn.

Hoạt động khám phá 5 trang 68 Toán 11 Tập 1
Dựng một dãy hình vuông bằng cách ghép từ các hình vuông đơn vị (cạnh bằng 1 đơn vị độ dài) theo các bước như Hình 4. Kí hiệu un (đơn vị diện tích) là diện tích hình vuông dựng được ở bước thứ n.
Giải bài tập Bài 2: Giới hạn của hàm số

Bài 1 trang 79 Toán 11 Tập 1
Tìm các giới hạn sau. Bài 1 trang 79 Toán 11 Tập 1

Bài 2 trang 79 Toán 11 Tập 1
Bài 2 trang 79 Toán 11 Tập 1

Bài 3 trang 79 Toán 11 Tập 1
Tìm các giới hạn sau. Bài 3 trang 79 Toán 11 Tập 1

Bài 4 trang 79 Toán 11 Tập 1
Tìm các giới hạn sau. Bài 4 trang 79 Toán 11 Tập 1

Bài 5 trang 79 Toán 11 Tập 1
Trong hồ có chứa 6 000 lít nước ngọt. Người ta bơm nước biển có nồng độ muối là 30 gam/lít vào hồ với tốc độ 15 lít/phút. Bài 5 trang 79 Toán 11 Tập 1
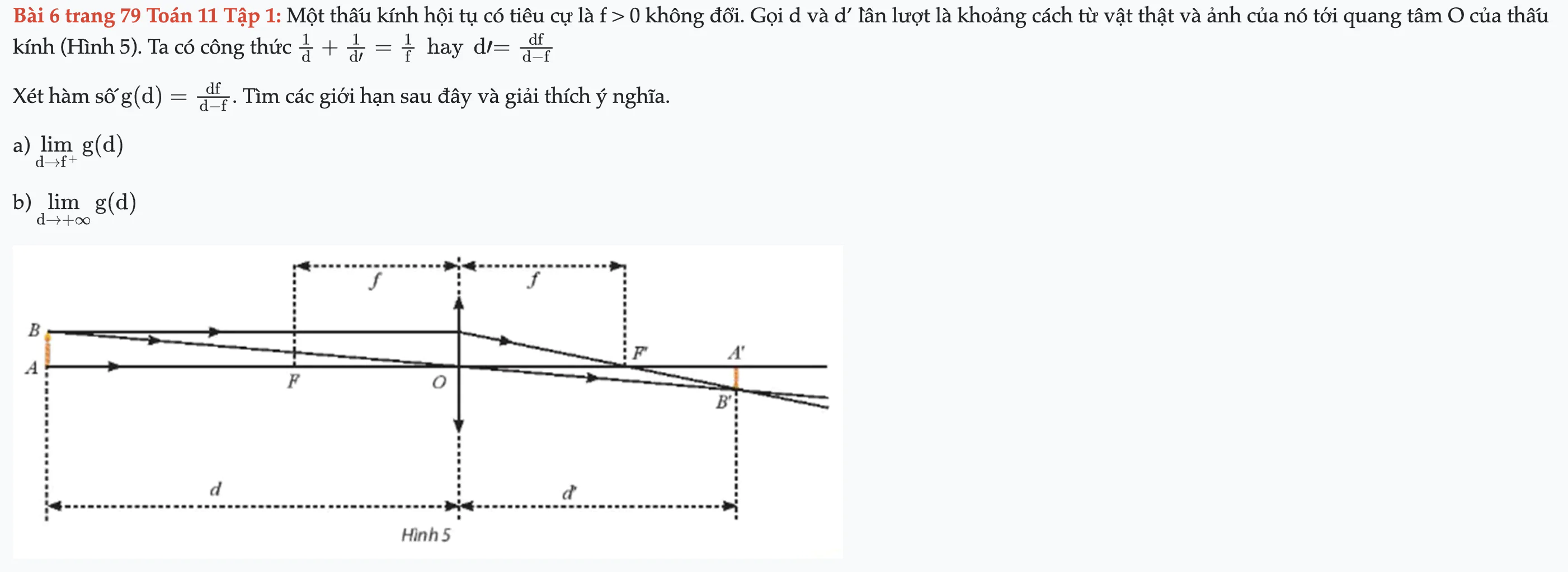
Bài 6 trang 79 Toán 11 Tập 1
Một thấu kính hội tụ có tiêu cự là f > 0 không đổi. Gọi d và d’ lần lượt là khoảng cách từ vật thật và ảnh của nó tới quang tâm O của thấu kính (Hình 5). Bài 6 trang 79 Toán 11 Tập 1
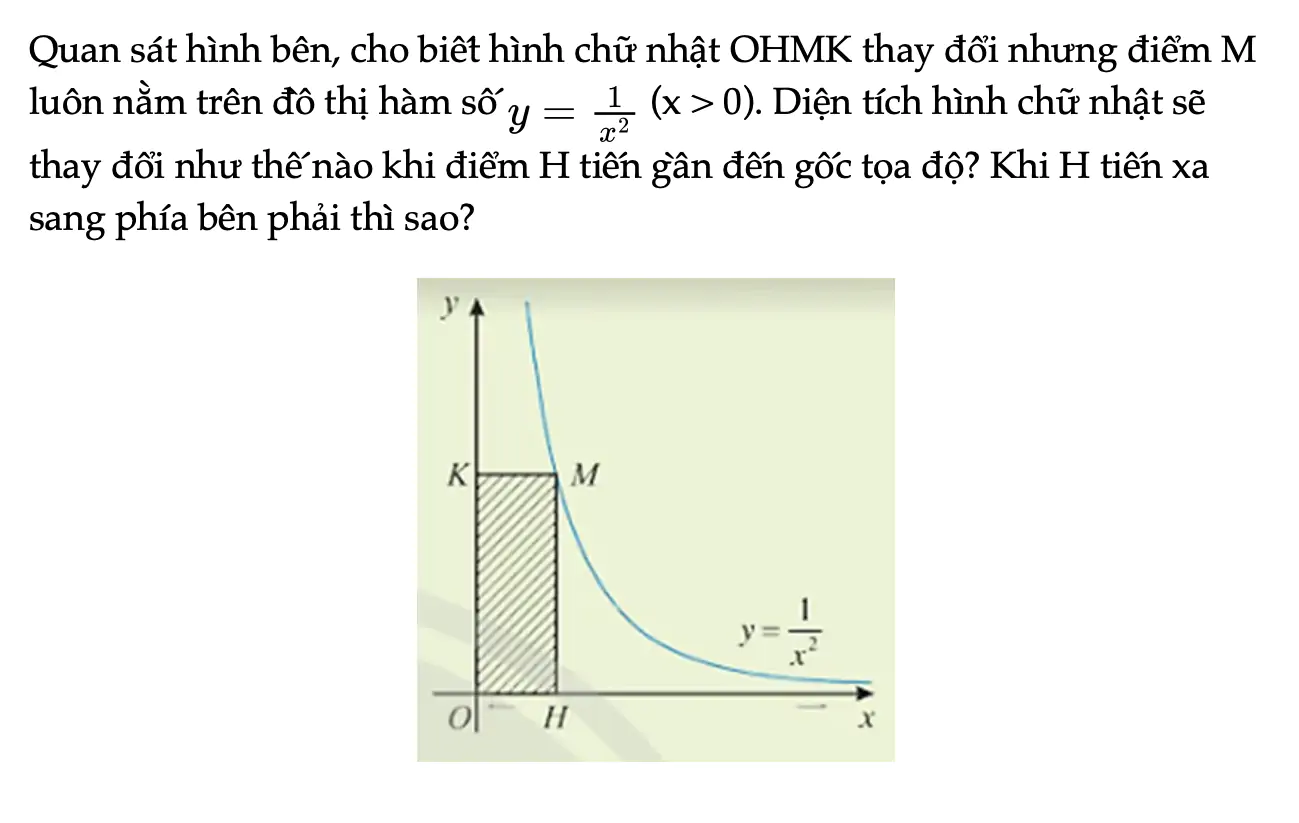
Hoạt động khởi động trang 71 Toán 11 Tập 1
Quan sát hình bên, cho biết hình chữ nhật OHMK thay đổi nhưng điểm M luôn nằm trên đồ thị hàm số y (x > 0). Diện tích hình chữ nhật sẽ thay đổi như thế nào khi điểm H tiến gần đến gốc tọa độ? Khi H tiến xa sang phía bên phải thì sao?

Hoạt động khám phá 1 trang 71 Toán 11 Tập 1
Xét hàm số y. a) Bảng sau đây cho biết giá trị của hàm số tại một số điểm gần điểm 1.Có nhận xét gì về giá trị của hàm số khi x càng gần đến 1? b) Ở Hình 1, M là điểm trên đồ thị hàm số y = f(x);

Thực hành 1 trang 72 Toán 11 Tập 1
Tìm các giới hạn sau.
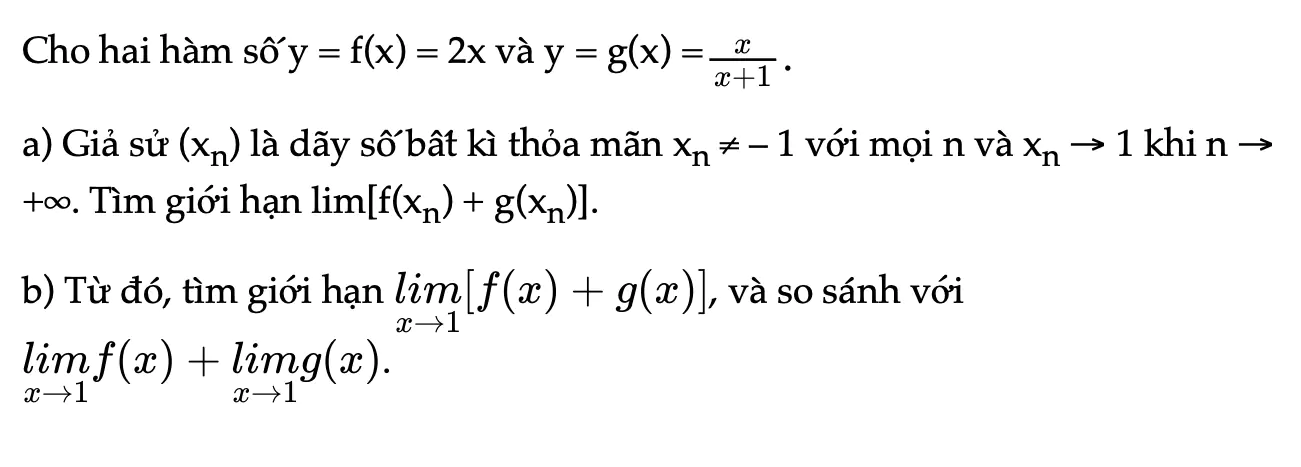
Hoạt động khám phá 2 trang 72 Toán 11 Tập 1
Cho hai hàm số y = f(x) và y = g(x). Thực hiện yêu cầu bài toán.
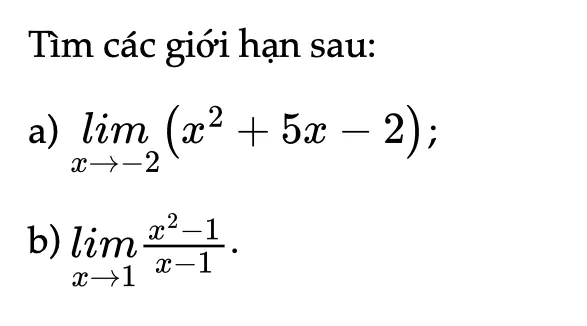
Thực hành 2 trang 73 Toán 11 Tập 1
Tìm các giới hạn sau.
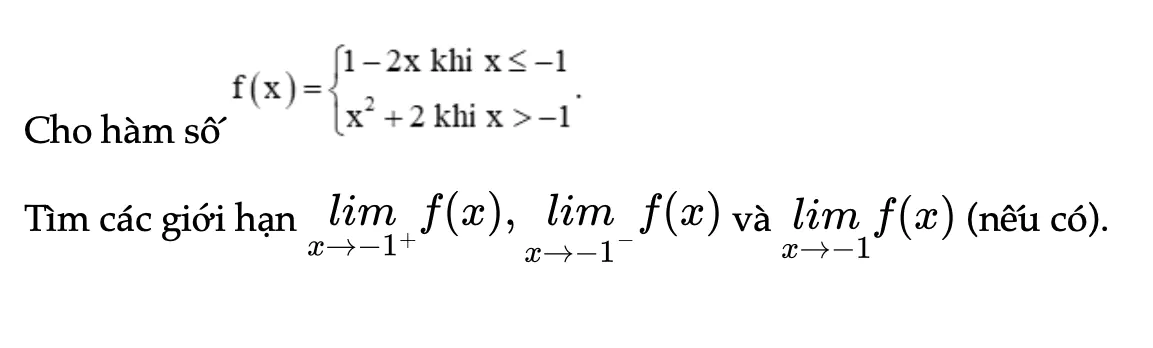
Thực hành 3 trang 75 Toán 11 Tập 1
Cho hàm số f(x). Tìm các giới hạn của hàm số.

Hoạt động khám phá 4 trang 75 Toán 11 Tập 1
Cho hàm số f(x)=1/x có đồ thị như Hình 3. Thực hiện yêu cầu bài toán.
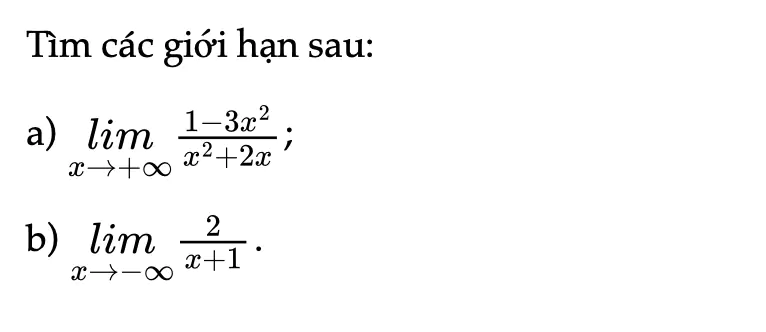
Thực hành 4 trang 76 Toán 11 Tập 1
Tìm các giới hạn sau.

Vận dụng 1 trang 76 Toán 11 Tập 1
Một cái hồ đang chứa 200m3 nước mặn với nồng độ muối 10kg/m3. Người ta ngọt hóa nước hồ bằng cách bơm nước ngọt vào hồ với tốc độ 2m3/phút. a) Viết biểu thức C(t) biểu thị nồng độ muối trong hồ sau t phút kể từ khi bắt đầu bơm.

Hoạt động khám phá 5 trang 77 Toán 11 Tập 1
Cho hàm số f(x) có đồ thị như Hình 4. a) Tìm các giá trị còn thiếu trong bảng. Từ đồ thị và bảng trên, có nhận xét gì về giá trị f(x) khi x dần tới 1 phía bên phải? b) Từ đồ thị và bảng trên, có nhận xét gì về giá trị f(x) khi x dần tới 1 phía bên trái.
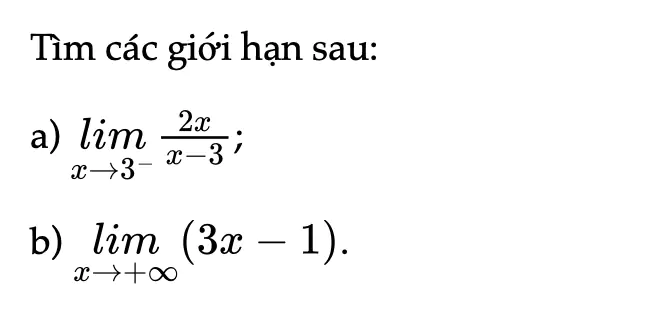
Thực hành 5 trang 78 Toán 11 Tập 1
Tìm các giới hạn sau.

Vận dụng 2 trang 78 Toán 11 Tập 1
Xét tình huống ở hoạt động khởi động đầu bài học. Gọi x là hoành độ điểm H. Tính diện tích S(x) của hình chữ nhật OHMK theo x. Diện tích này thay đổi như thế nào khi x → 0+ và khi x → +∞.
Giải bài tập Bài 3: Hàm số liên tục

Bài 1 trang 84 Toán 11 Tập 1
Xét tính liên tục của hàm số sau. Bài 1 trang 84 Toán 11 Tập 1

Bài 2 trang 84 Toán 11 Tập 1
Cho hàm số f(x). Tìm a để hàm số f(x) liên tục trên ℝ. Bài 2 trang 84 Toán 11 Tập 1

Bài 3 trang 85 Toán 11 Tập 1
Xét tính liên tục của hàm số sau. Bài 3 trang 85 Toán 11 Tập 1

Bài 4 trang 85 Toán 11 Tập 1
Bài 4 trang 85 Toán 11 Tập 1

Bài 5 trang 85 Toán 11 Tập 1
Một bãi đậu xe ô tô đưa ra giá C(x) (đồng) khi thời gian đậu xe là x (giờ) như sau. Bài 5 trang 85 Toán 11 Tập 1

Bài 6 trang 85 Toán 11 Tập 1
Lực hấp dẫn do Trái Đất tác dụng lên một đơn vị khối lượng ở khoảng cách r tính từ tâm của nó là F(r). Bài 6 trang 85 Toán 11 Tập 1

Hoạt động khởi động trang 80 Toán 11 Tập 1
Hai đồ thị ở hai hình dưới đây cho biết phí gửi xe y của ô tô con (tính theo 10 nghìn đồng) theo thời gian gửi x (tính theo giờ) của hai bãi xe. Có nhận xét gì về sự thay đổi của số tiền phí phải trả theo thời gian gửi ở mỗi bãi đỗ xe?

Hoạt động khám phá 1 trang 80 Toán 11 Tập 1
Cho hàm số y=f(x) có đồ thị như Hình 1. Thực hiện yêu cầu bài toán.

Thực hành 1 trang 81 Toán 11 Tập 1
Xét tính liên tục của hàm số sau.

Hoạt động khám phá 2 trang 81 Toán 11 Tập 1
Cho hàm số y=f(x). a) Xét tính liên tục của hàm số tại mỗi điểm x0 ∈ (1; 2).
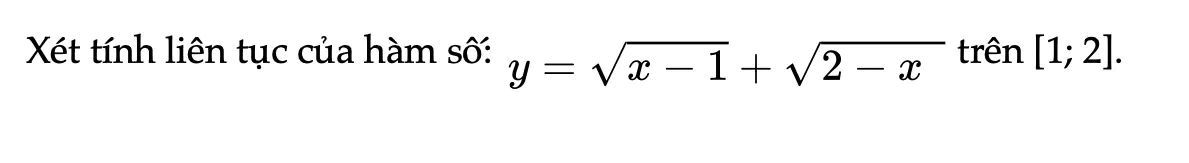
Thực hành 2 trang 82 Toán 11 Tập 1
Xét tính liên tục của hàm số sau.

Vận dụng 1 trang 82 Toán 11 Tập 1
Tại một xưởng sản xuất bột đá thạch anh, giá bán (tính theo nghìn đồng) của x (kg) bột đá thạch anh được tính theo công thức: a) Với k = 0, xét tính liên tục của hàm số P(x) trên (0; +∞). b) Với giá trị nào của k thì hàm số P(x) liên tục trên (0; +∞).
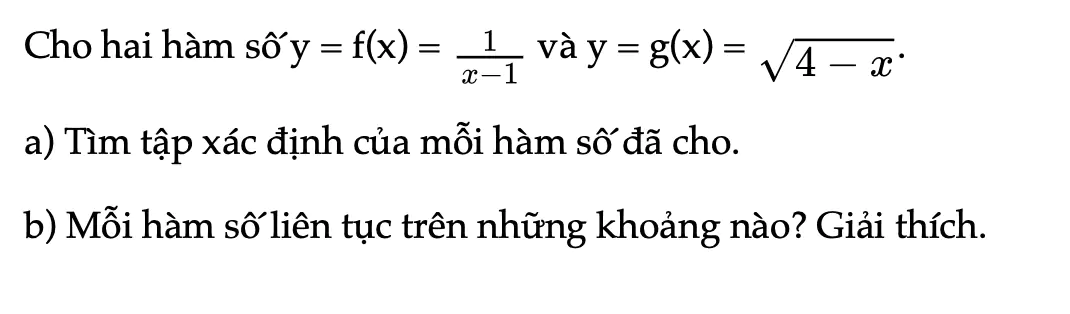
Hoạt động khám phá 3 trang 82 Toán 11 Tập 1
Cho hai hàm số y = f(x) và y = g(x). a) Tìm tập xác định của mỗi hàm số đã cho. b) Mỗi hàm số liên tục trên những khoảng nào? Giải thích.
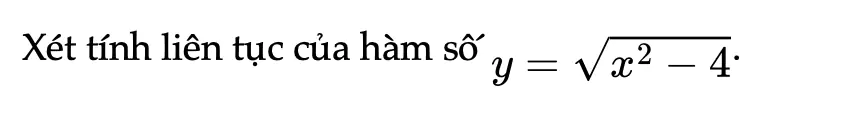
Thực hành 3 trang 83 Toán 11 Tập 1
Xét tính liên tục của hàm số y.
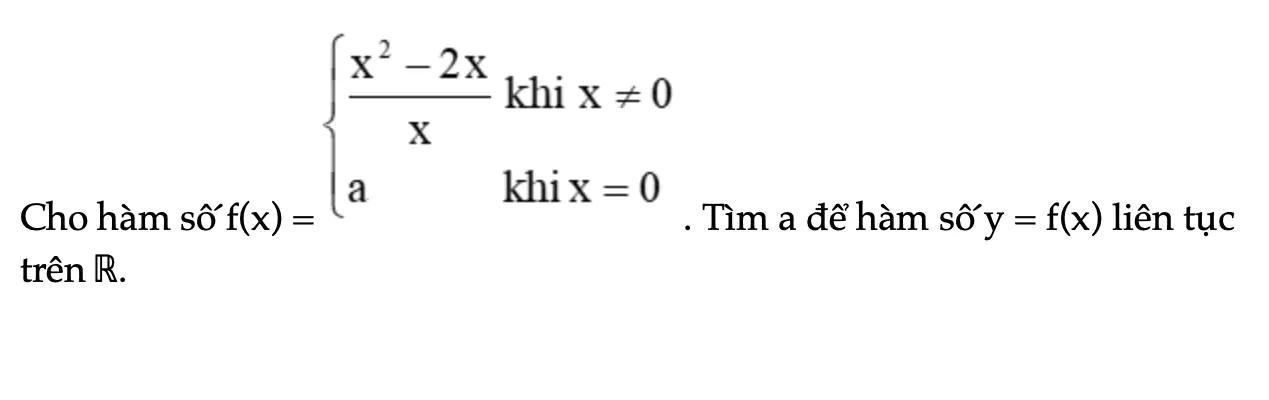
Thực hành 4 trang 83 Toán 11 Tập 1
Cho hàm số f(x). Tìm a để hàm số y = f(x) liên tục trên ℝ.

Vận dụng 2 trang 83 Toán 11 Tập 1
Một hãng taxi đưa ra giá cước T(x) (đồng) khi đi quãng đường x (km) cho loại xe 4 chỗ như sau. Xét tính liên tục của hàm số T(x).
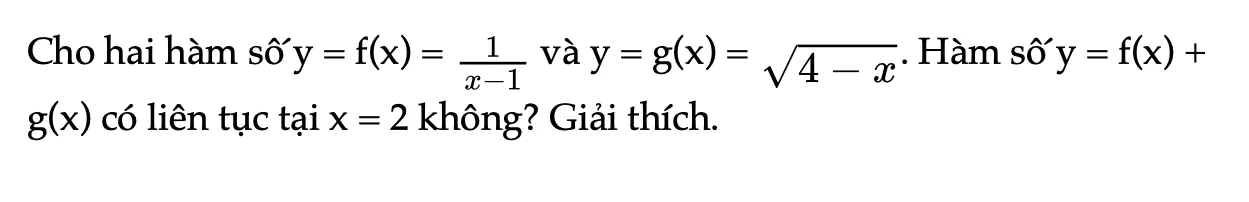
Hoạt động khám phá 4 trang 83 Toán 11 Tập 1
Cho hai hàm số y = f(x) và y = g(x). Hàm số y = f(x) + g(x) có liên tục tại x = 2 không? Giải thích.
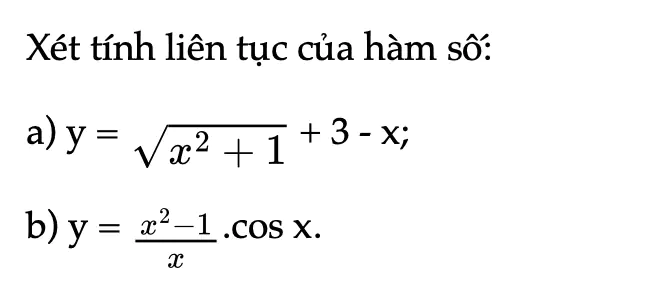
Thực hành 5 trang 84 Toán 11 Tập 1
Xét tính liên tục của hàm số.

Vận dụng 3 trang 84 Toán 11 Tập 1
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) tâm O, bán kính bằng 1. Một đường thẳng d thay đổi, luôn vuông góc với trục hoành, cắt trục hoành tại điểm M có hoành độ x (– 1 < x < 1) và cắt đường tròn (C) tại các điểm N và P (xem Hình 6).
Giải bài tập Bài tập cuối chương 3

Bài 1 trang 85 Toán 11 Tập 1
Bài 1 trang 85 Toán 11 Tập 1

Bài 2 trang 85 Toán 11 Tập 1
Tổng của cấp số nhân lùi vô hạn. Bài 2 trang 85 Toán 11 Tập 1

Bài 3 trang 85 Toán 11 Tập 1
Bài 3 trang 85 Toán 11 Tập 1

Bài 4 trang 85 Toán 11 Tập 1
Hàm số: f(x) liên tục tại x = 2 khi. Bài 4 trang 85 Toán 11 Tập 1

Bài 5 trang 85 Toán 11 Tập 1
Bài 5 trang 85 Toán 11 Tập 1

Bài 6 trang 86 Toán 11 Tập 1
Tìm các giới hạn sau. Bài 6 trang 86 Toán 11 Tập 1

Bài 7 trang 86 Toán 11 Tập 1
Cho tam giác đều có cạnh bằng a, gọi là tam giác H1. Nỗi các trung điểm của H1 để tạo thành tam giác H2. Tiếp theo, nối các trung điểm của H2 để tạo thành tam giác H3 (Hình 1). Bài 7 trang 86 Toán 11 Tập 1

Bài 8 trang 86 Toán 11 Tập 1
Tìm các giới hạn sau. Bài 8 trang 86 Toán 11 Tập 1

Bài 9 trang 86 Toán 11 Tập 1
Tìm các giới hạn sau. Bài 9 trang 86 Toán 11 Tập 1

Bài 10 trang 86 Toán 11 Tập 1
Tìm các giới hạn sau. Bài 10 trang 86 Toán 11 Tập 1
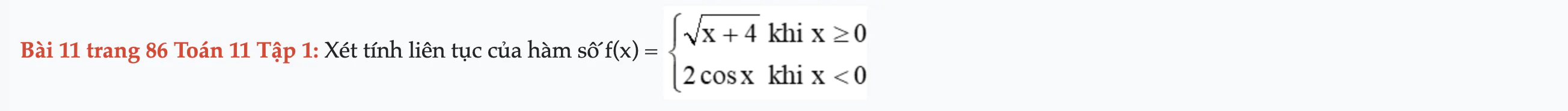
Bài 11 trang 86 Toán 11 Tập 1
Xét tính liên tục của hàm số f(x). Bài 11 trang 86 Toán 11 Tập 1
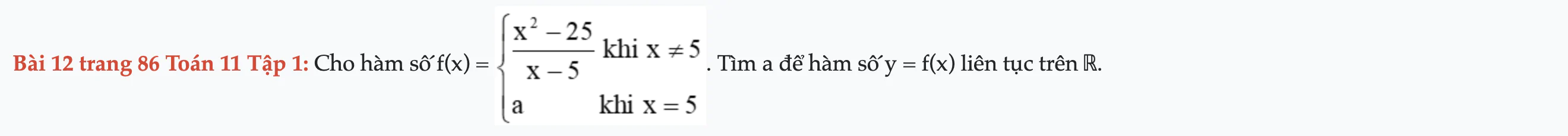
Bài 12 trang 86 Toán 11 Tập 1
Cho hàm số f(x). Tìm a để hàm số y = f(x) liên tục trên ℝ. Bài 12 trang 86 Toán 11 Tập 1

Bài 13 trang 86 Toán 11 Tập 1
Trong một tủ thí nghiệm, nhiệt độ trong tủ sấy được điều khiển tăng từ 10°C, mỗi phút tăng 2°C trong 60 phút, sau đó giảm mỗi phút 3°C trong 40 phút. Hàm số biểu thị nhiệt độ (tính theo ºC) trong tủ theo thời gian t. Bài 13 trang 86 Toán 11 Tập 1