Giải bài tập Toán 11 Chương 1: Hàm số lượng giác và phương trình lượng giác | Chân trời sáng tạo
Hướng dẫn giải chi tiết Chương 1: Hàm số lượng giác và phương trình lượng giác
Giải bài tập Bài 1: Góc lượng giác

Bài 1 trang 12 Toán 11 Tập 1
Đổi số đo của các góc dưới đây sang radian. Bài 1 trang 12 Toán 11 Tập 1

Bài 2 trang 12 Toán 11 Tập 1
Đổi số đo của các góc sau đây sang độ. Bài 2 trang 12 Toán 11 Tập 1

Bài 3 trang 12 Toán 11 Tập 1
Biểu diễn các góc lượng giác sau trên đường tròn lượng giác. Bài 3 trang 12 Toán 11 Tập 1

Bài 4 trang 12 Toán 11 Tập 1
Góc lượng giác trên có cùng điểm biểu diễn trên đường tròn lượng giác với góc lượng giác nào dưới đây. Bài 4 trang 12 Toán 11 Tập 1

Bài 5 trang 12 Toán 11 Tập 1
Viết các công thức số đo tổng quát của các góc lượng giác (OA, OM) và (OA, ON) trong Hình 14. Bài 5 trang 12 Toán 11 Tập 1

Bài 6 trang 12 Toán 11 Tập 1
Trong Hình 15, mâm bánh xe ô tô được chia thành năm phần bằng nhau. Viết công thức số đo tổng quát của góc lượng giác (Ox, ON). Bài 6 trang 12 Toán 11 Tập 1

Bài 7 trang 13 Toán 11 Tập 1
Trên đường tròn lượng giác hãy biểu diễn các góc lượng giác có số đo có dạng là. Bài 7 trang 13 Toán 11 Tập 1

Bài 8 trang 13 Toán 11 Tập 1
Vị trí các điểm B, C, D trên cánh quạt động cơ máy bay trong Hình 16 có thể biểu diễn cho các góc lượng giác nào sau đây. Bài 8 trang 13 Toán 11 Tập 1

Bài 9 trang 13 Toán 11 Tập 1
Hải lí là một đơn vị chiều dài hàng hải, được tính bằng độ dài một cung chắn một góc α của đường kinh tuyến (Hình 17). Đổi số đo α sang radian và cho biết 1 hải lí bằng khoảng bao nhiêu ki lô mét. Bài 9 trang 13 Toán 11 Tập 1

Hoạt động khởi động trang 7 Toán 11 Tập 1
Mỗi hình dưới đây thể hiện chuyển động quay của một điểm trên bánh lái tàu từ vị trí A đến vị trí B. Các chuyển động này có điểm nào giống nhau, điểm nào khác nhau?

Hoạt động khám phá 1 trang 7 Toán 11 Tập 1
Một chiếc bánh lái tàu có thể quay theo cả hai chiều. Trong Hình 1 và Hình 2, lúc đầu thanh OM ở vị trí OA.
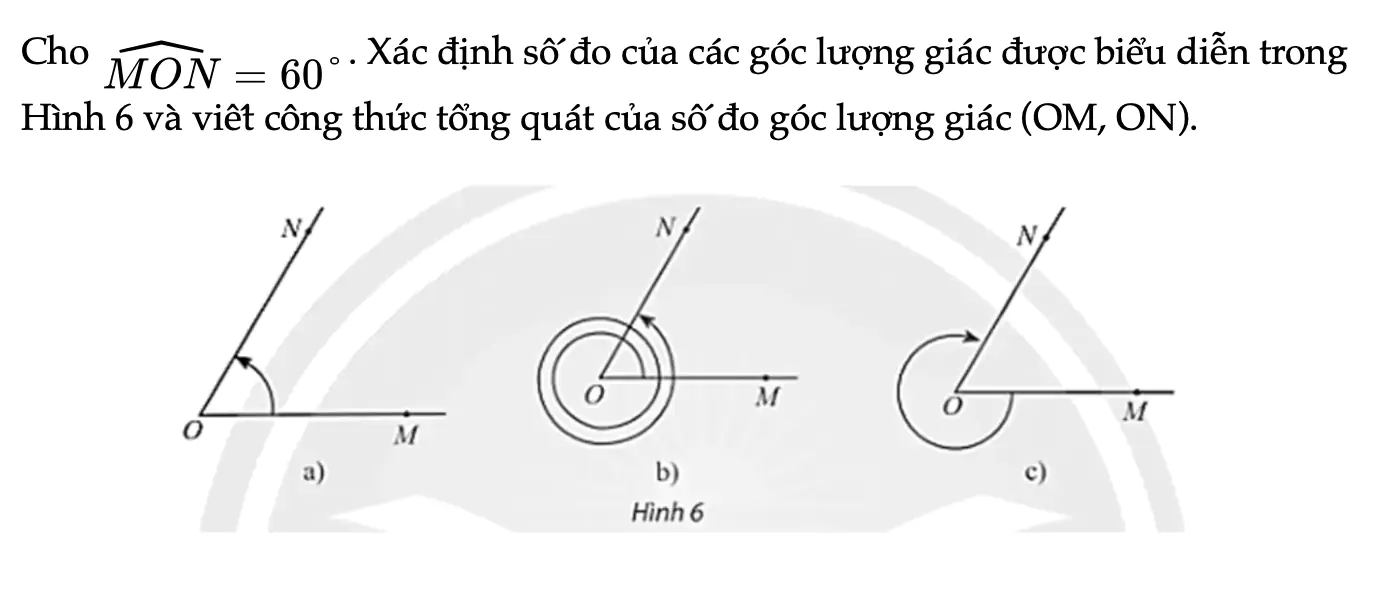
Thực hành 1 trang 9 Toán 11 Tập 1
Cho góc MON = 60°. Xác định số đo của các góc lượng giác được biểu diễn trong Hình 6 và viết công thức tổng quát của số đo góc lượng giác (OM, ON).

Vận dụng 1 trang 9 Toán 11 Tập 1
Trong các khoảng thời gian từ 0 giờ đến 2 giờ 15 phút, kim phút quét một góc lượng giác bao nhiêu độ?
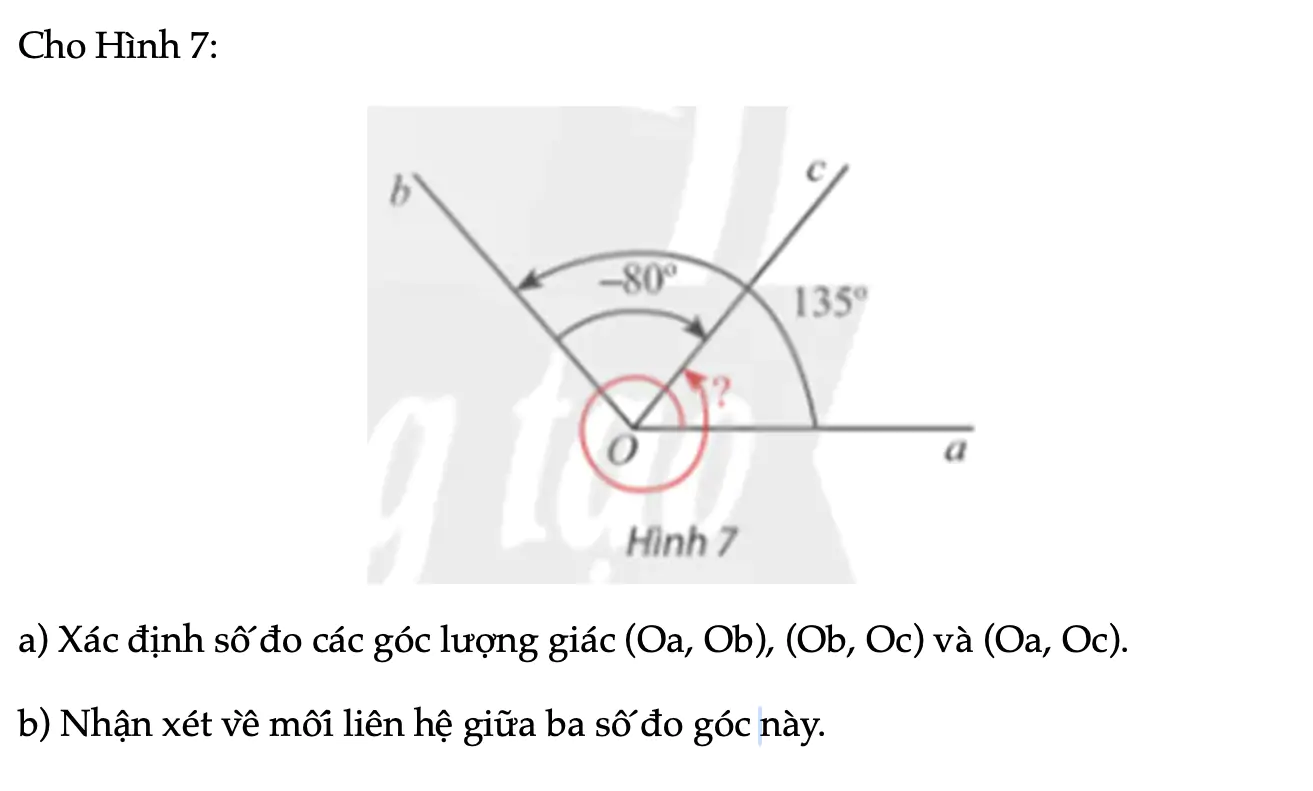
Hoạt động khám phá 2 trang 9 Toán 11 Tập 1
Cho Hình 7: a) Xác định số đo các góc lượng giác (Oa, Ob), (Ob, Oc) và (Oa, Oc). b) Nhận xét về mối liên hệ giữa ba số đo góc này.
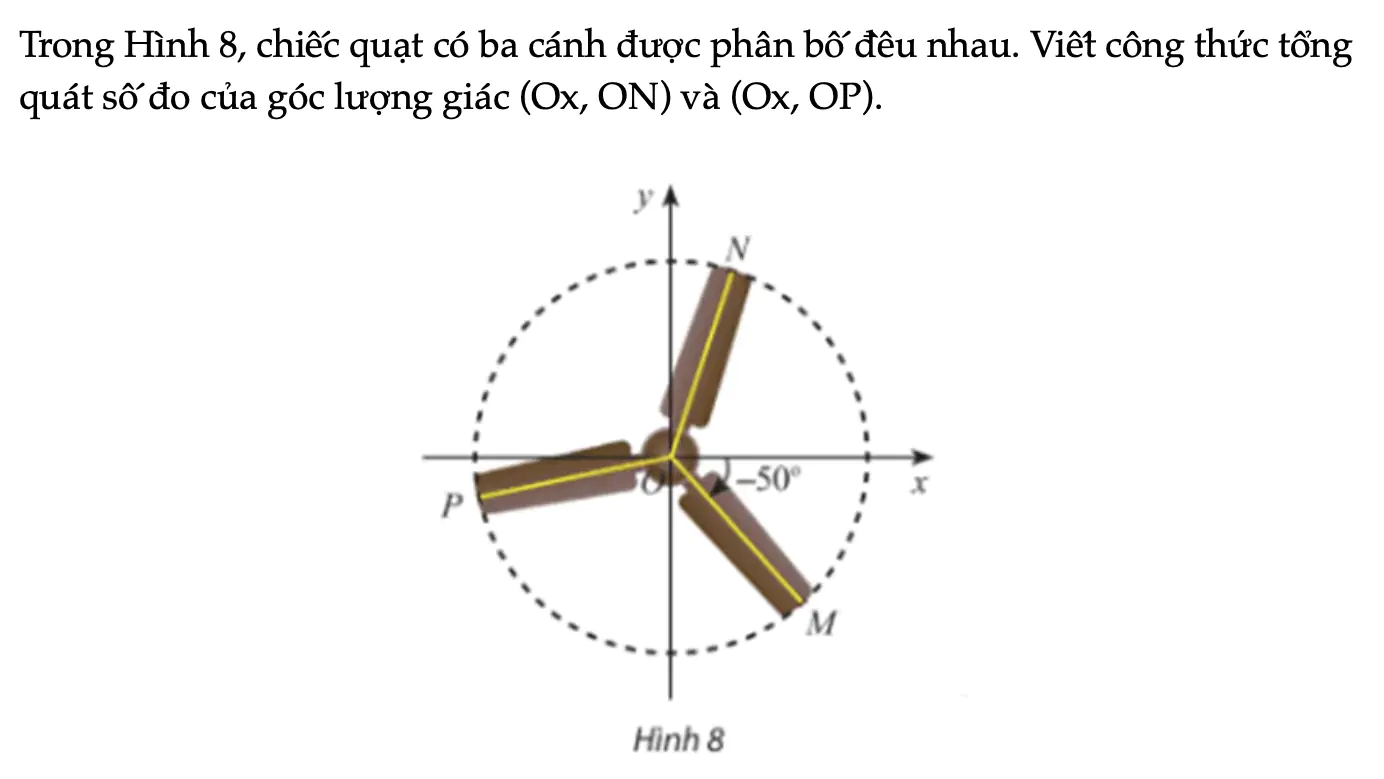
Vận dụng 2 trang 9 Toán 11 Tập 1
Trong Hình 8, chiếc quạt có ba cánh được phân bố đều nhau. Viết công thức tổng quát số đo của góc lượng giác (Ox, ON) và (Ox, OP).
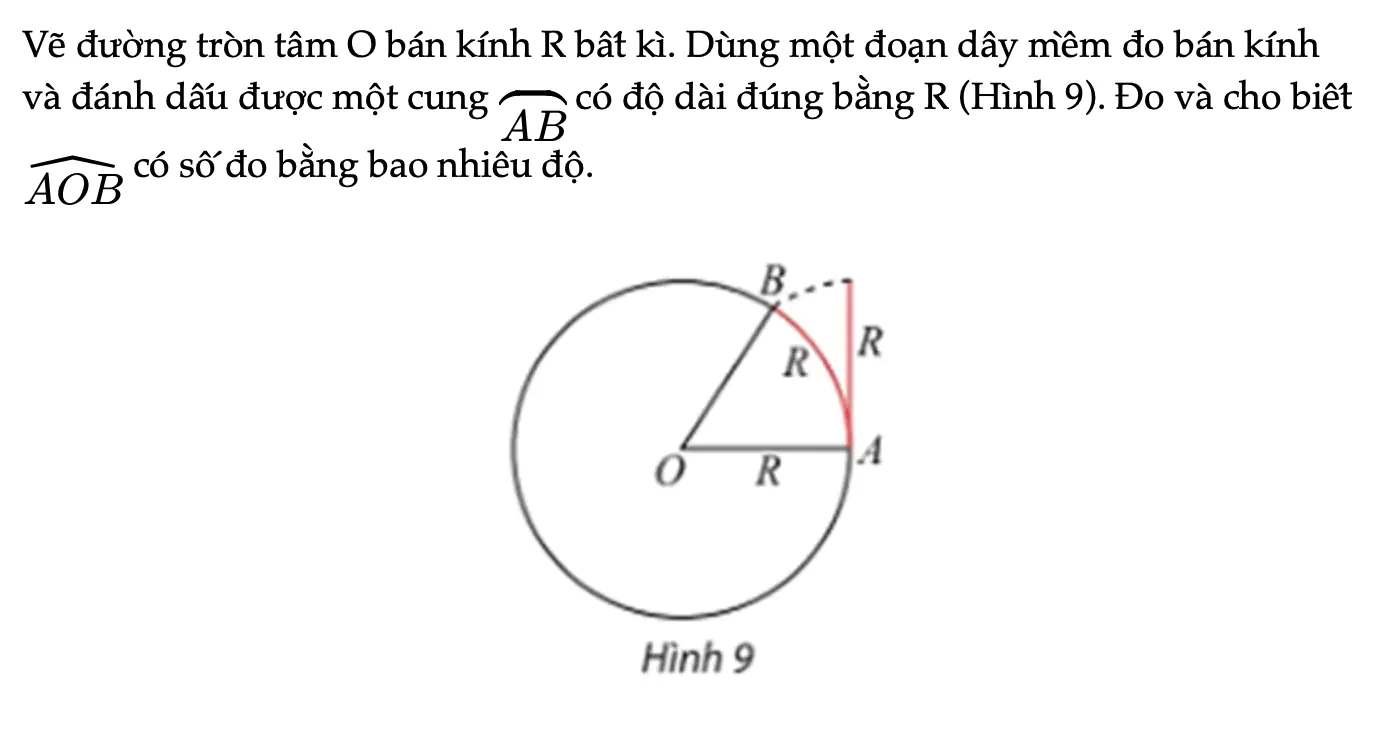
Hoạt động khám phá 3 trang 10 Toán 11 Tập 1
Vẽ đường tròn tâm O bán kính R bất kì. Dùng một đoạn dây mềm đo bán kính và đánh dấu được một cung AB có độ dài đúng bằng R (Hình 9). Đo và cho biết góc AOB có số đo bằng bao nhiêu độ.

Thực hành 2 trang 11 Toán 11 Tập 1
Hoàn thành bảng chuyển đổi đơn vị đo của các góc sau đây:

Hoạt động khám phá 4 trang 11 Toán 11 Tập 1
Trong mặt phẳng tọa độ Oxy, vẽ đường tròn tâm O bán kính bằng 1 và điểm A(1; 0). a) Cho điểm B(0; 1). Số đo góc lượng giác (OA, OB) bằng bao nhiêu radian? b) Xác định các điểm A’ và B’ trên đường tròn.

Thực hành 3 trang 12 Toán 11 Tập 1
Biểu diễn trên đường tròn lượng giác các góc lượng giác có số đo là:
Giải bài tập Bài 2: Giá trị lượng giác của một góc lượng giác

Bài 1 trang 19 Toán 11 Tập 1
Các đẳng thức sau có thể đồng thời xảy ra không. Bài 1 trang 19 Toán 11 Tập 1
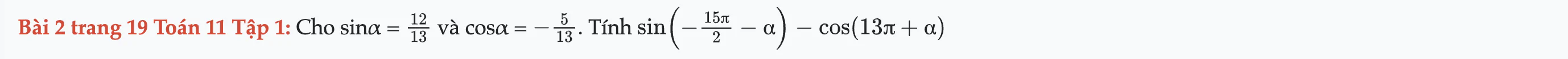
Bài 2 trang 19 Toán 11 Tập 1
Bài 2 trang 19 Toán 11 Tập 1

Bài 3 trang 19 Toán 11 Tập 1
Tính các giá trị lượng giác của góc α, nếu. Bài 3 trang 19 Toán 11 Tập 1

Bài 4 trang 19 Toán 11 Tập 1
Biểu diễn các giá trị lượng giác sau qua các giá trị lượng giác của góc có số đo từ 0 đến π/4 hoặc từ 0 đến 45° và tính. Bài 4 trang 19 Toán 11 Tập 1

Bài 5 trang 19 Toán 11 Tập 1
Chứng minh đẳng thức lượng giác sau. Bài 5 trang 19 Toán 11 Tập 1

Bài 6 trang 19 Toán 11 Tập 1
Rút gọn các biểu thức sau. Bài 6 trang 19 Toán 11 Tập 1

Bài 7 trang 20 Toán 11 Tập 1
Thanh OM quay ngược chiều kim đồng hồ quanh trục O của nó trên một mặt phẳng thẳng đứng và in bóng vuông góc xuống mặt đất như Hình 12. Vị trí ban đầu của thanh là OA. Bài 7 trang 20 Toán 11 Tập 1

Bài 8 trang 20 Toán 11 Tập 1
Khi đạp xe di chuyển, van V của bánh xe quay quanh trục O theo chiều kim đồng hồ với tốc độ góc không đổi là 11 rad/s (Hình 13). Ban đầu van nằm ở vị trí A. Bài 8 trang 20 Toán 11 Tập 1
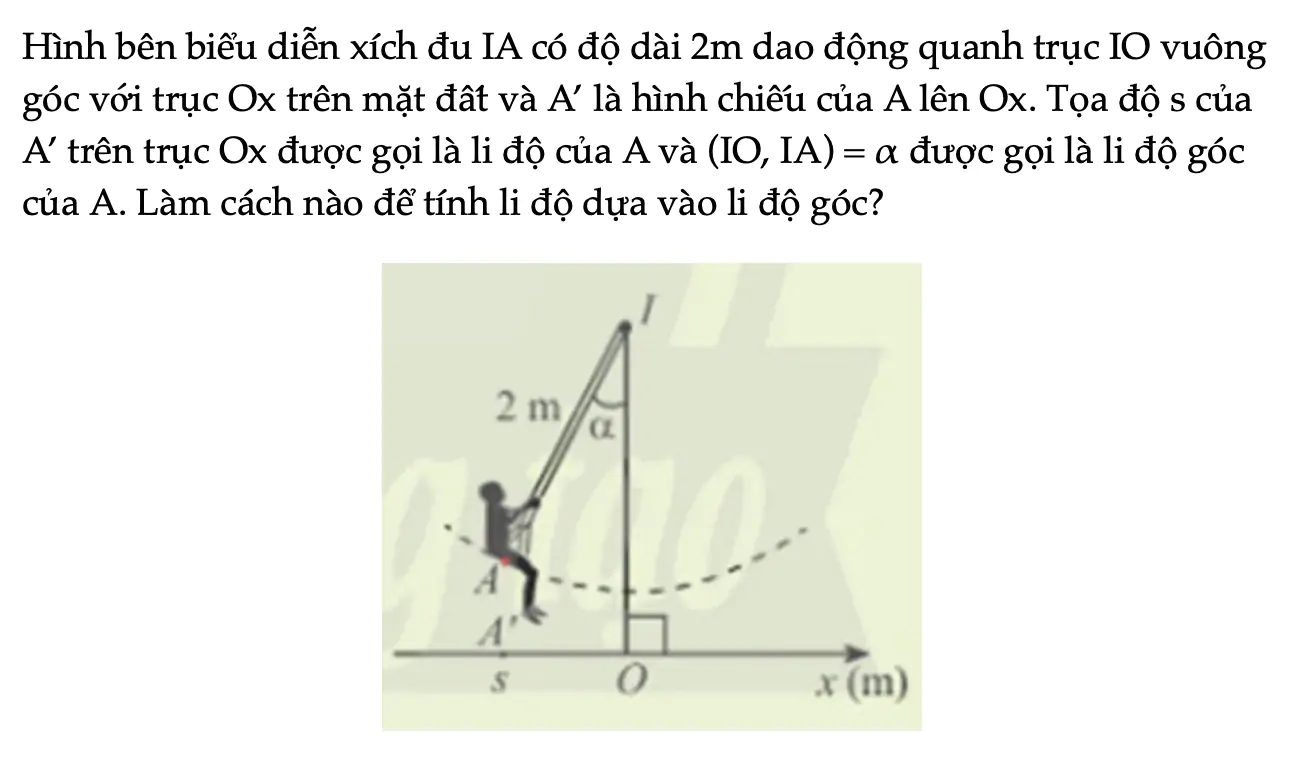
Hoạt động khởi động trang 13 Toán 11 Tập 1
Hình bên biểu diễn xích đu IA có độ dài 2m dao động quanh trục IO vuông góc với trục Ox trên mặt đất và A’ là hình chiếu của A lên Ox. Tọa độ s của A’ trên trục Ox được gọi là li độ của A và (IO, IA) = α được gọi là li độ góc của A. Tính:
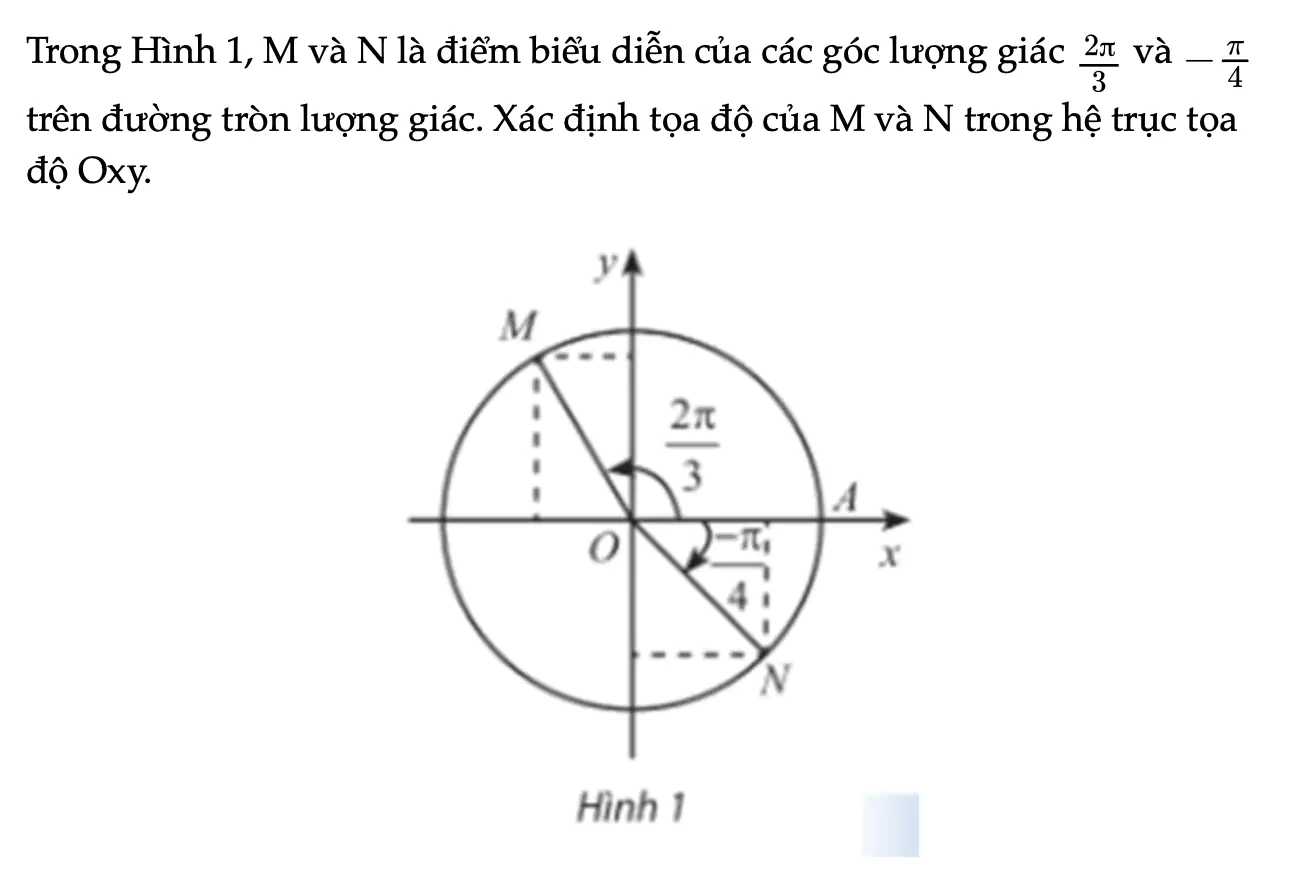
Hoạt động khám phá 1 trang 13 Toán 11 Tập 1
Trong Hình 1, M và N là điểm biểu diễn của các góc lượng giác sau trên đường tròn lượng giác. Xác định tọa độ của M và N trong hệ trục tọa độ Oxy.
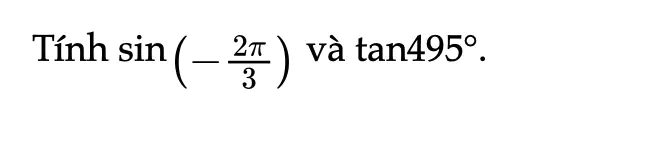
Thực hành 1 trang 15 Toán 11 Tập 1
Tính giá trị lượng giác của các góc sau.

Thực hành 2 trang 16 Toán 11 Tập 1
Sử dụng máy tính cầm tay để tính giá trị lượng giác của một góc lượng giác.

Hoạt động khám phá 2 trang 16 Toán 11 Tập 1
a) Trong Hình 5, M là điểm biểu diễn của góc lượng giác α trên đường tròn lượng giác. Giải thích vì sao sin2α + cos2α = 1. b) Chia cả hai vễ của biểu thức ở câu a) cho cos2α ta được đẳng thức nào?
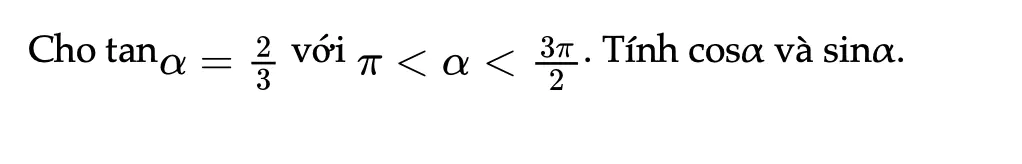
Thực hành 3 trang 17 Toán 11 Tập 1
Tính giá trị lượng giác của các góc sau.

Hoạt động khám phá 3 trang 17 Toán 11 Tập 1
Cho α. Biểu diễn các góc lượng giác trên đường tròn lượng giác và rút ra mối liên hệ giữa giá trị lượng giác của các góc này với giá trị lượng giác của góc α.

Thực hành 4 trang 19 Toán 11 Tập 1
a) Biểu diễn cos638° qua giá trị lượng giác của góc có số đo từ 0° đến 45°.
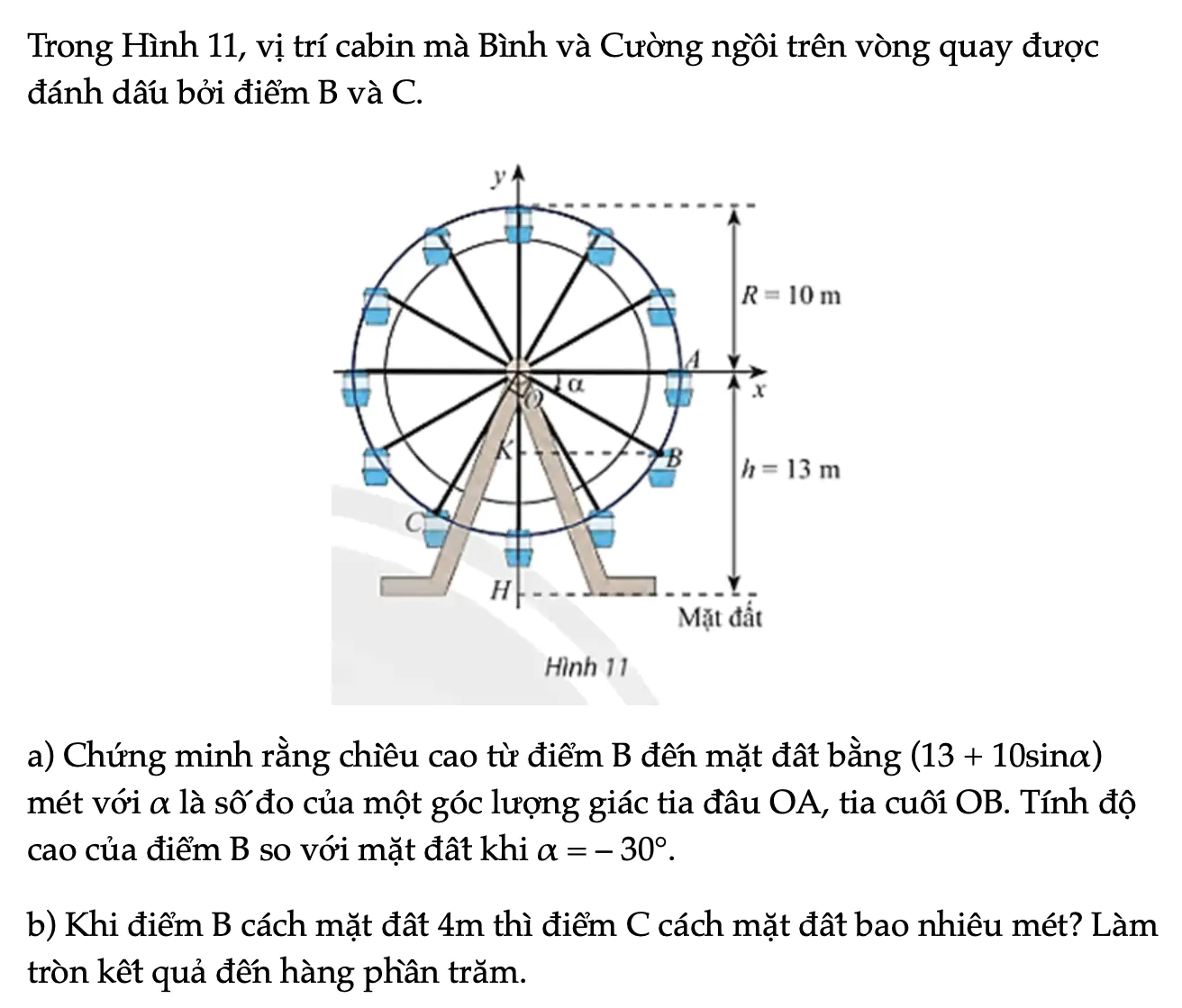
Vận dụng trang 19 Toán 11 Tập 1
Trong Hình 11, vị trí cabin mà Bình và Cường ngồi trên vòng quay được đánh dấu bởi điểm B và C. Thực hiện các yêu cầu bài toán.
Giải bài tập Bài 3: Các công thức lượng giác

Bài 1 trang 23 Toán 11 Tập 1
Không dùng máy tính cầm tay, tính các giá trị lượng giác của các góc. Bài 1 trang 23 Toán 11 Tập 1
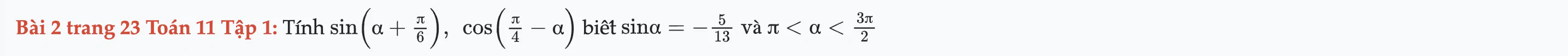
Bài 2 trang 23 Toán 11 Tập 1
Bài 2 trang 23 Toán 11 Tập 1

Bài 3 trang 24 Toán 11 Tập 1
Tính các giá trị lượng giác của góc 2α, biết. Bài 3 trang 24 Toán 11 Tập 1

Bài 4 trang 24 Toán 11 Tập 1
Rút gọn các biểu thức sau. Bài 4 trang 24 Toán 11 Tập 1

Bài 5 trang 24 Toán 11 Tập 1
Tính các giá trị lượng giác của góc α, biết. Bài 5 trang 24 Toán 11 Tập 1
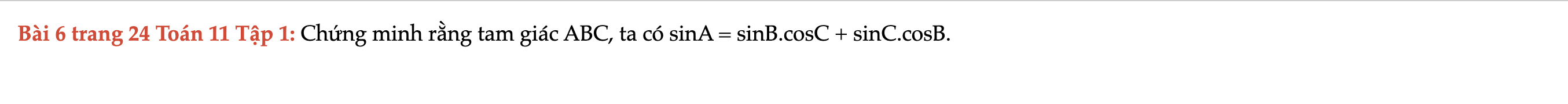
Bài 6 trang 24 Toán 11 Tập 1
Chứng minh rằng tam giác ABC, ta có sinA = sinB.cosC + sinC.cosB. Bài 6 trang 24 Toán 11 Tập 1

Bài 7 trang 24 Toán 11 Tập 1
Trong Hình 3, tam giác ABC vuông tại B và có hai cạnh góc vuông là AB = 4, BC = 3. Bài 7 trang 24 Toán 11 Tập 1

Bài 8 trang 24 Toán 11 Tập 1
Trong Hình 4, pít – tông M của động cơ chuyển động tịnh tiến qua lại dọc theo xi lanh làm quay trục khuỷu IA. Bài 8 trang 24 Toán 11 Tập 1
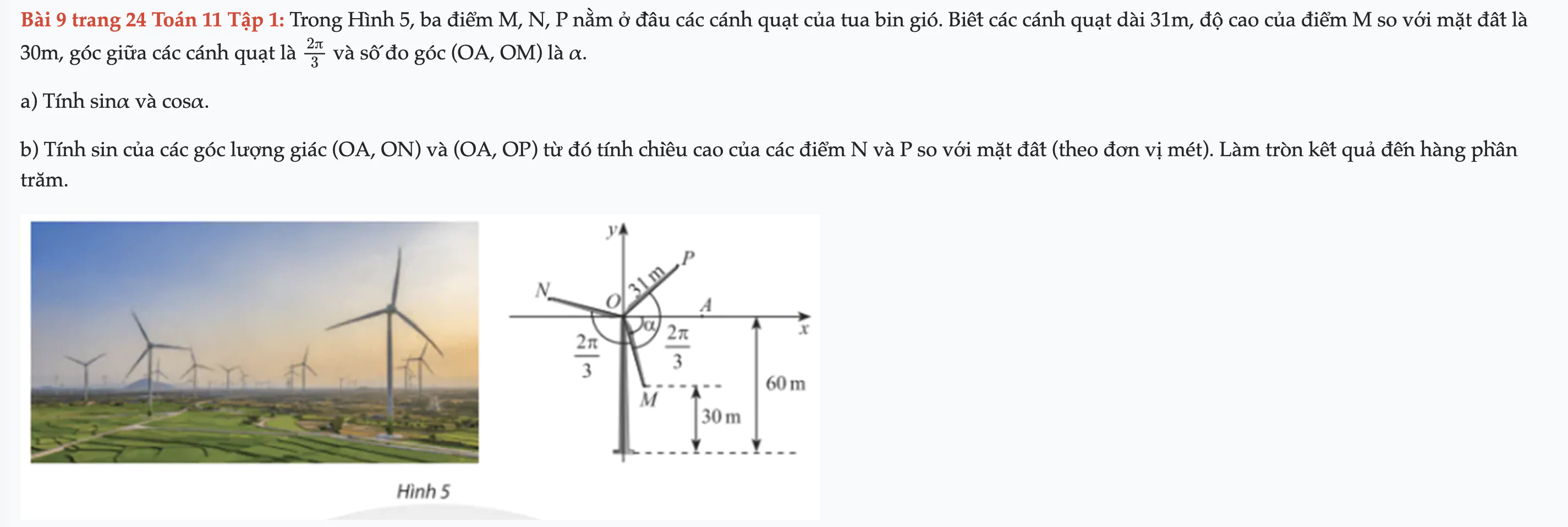
Bài 9 trang 24 Toán 11 Tập 1
Trong Hình 5, ba điểm M, N, P nằm ở đầu các cánh quạt của tua bin gió. Biết các cánh quạt dài 31m, độ cao của điểm M so với mặt đất là 30m. Bài 9 trang 24 Toán 11 Tập 1

Hoạt động khởi động trang 20 Toán 11 Tập 1
Trong kiến trúc, các vòm cổng bằng đá thường có hình nửa đường tròn để có thể chịu lực tốt. Trong hình bên, vòm cổng được ghép bởi sáu phiến đá hai bên tạo thành các cung AB, BC, CD, EF, FG, GH bằng nhau và một phiến đá chốt ở đỉnh.

Hoạt động khám phá 1 trang 21 Toán 11 Tập 1
Quan sát Hình 1. Từ hai cách tính tích vô hướng của vectơ OM và ON sau đây. Hãy suy ra công thức tính cos(α – β) theo các giá trị lượng giác của α và β. Từ đó, hãy suy ra công thức cos(α + β) bằng cách thay β bằng – β.
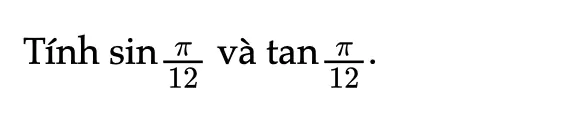
Thực hành 1 trang 21 Toán 11 Tập 1
Tính các giá trị lượng giác sau.

Hoạt động khám phá 2 trang 21 Toán 11 Tập 1
Hãy áp dụng công thức cộng cho trường hợp β = α và tính các giá trị lượng giác của góc 2α.

Hoạt động khám phá 3 trang 22 Toán 11 Tập 1
Từ công thức cộng, hãy tính tổng và hiệu của: a) cos(α – β) và cos(α + β) ; b) sin(α – β) và sin(α + β) .
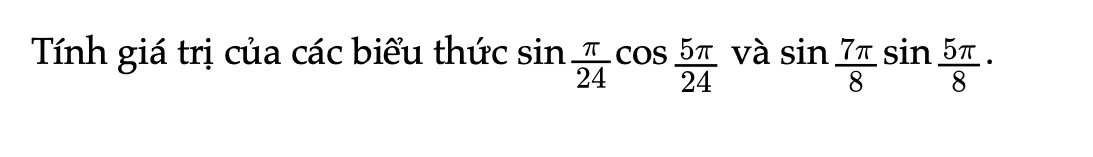
Thực hành 3 trang 22 Toán 11 Tập 1
Tính giá trị của các biểu thức sau.

Hoạt động khám phá 4 trang 22 Toán 11 Tập 1
Áp dụng công thức biến đổi tích thành tổng cho hai góc lượng giác a và b ta được các đẳng thức nào?

Vận dụng trang 23 Toán 11 Tập 1
Trong bài toán khởi động, cho biết vòm cổng rộng 120 cm và khoảng cách từ B đến đường kính AH là 27 cm. Tính sin α và cos α, từ đó tính khoảng cách từ điểm C đến đường kính AH. Làm tròn kết quả đến hàng phần mười.
Giải bài tập Bài 4: Hàm số lượng giác và đồ thị

Bài 1 trang 32 Toán 11 Tập 1
Các hàm số dưới đây có là hàm số chẵn hay hàm số lẻ không. Bài 1 trang 32 Toán 11 Tập 1

Bài 2 trang 32 Toán 11 Tập 1
Tìm tập xác định của các hàm số sau. Bài 2 trang 32 Toán 11 Tập 1

Bài 3 trang 33 Toán 11 Tập 1
Tìm tập giá trị của hàm số y = 2cosx + 1. Bài 3 trang 33 Toán 11 Tập 1
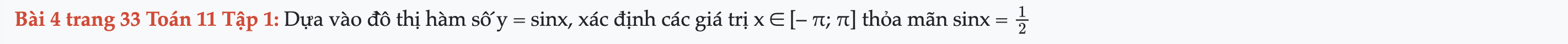
Bài 4 trang 33 Toán 11 Tập 1
Dựa vào đồ thị hàm số y = sinx, xác định các giá trị x ∈ [– π; π]. Bài 4 trang 33 Toán 11 Tập 1

Bài 5 trang 33 Toán 11 Tập 1
Khi đu quay hoạt động, vận tốc theo phương ngang của một cabin M phụ thuộc vào góc lượng giác α = (Ox, OM) theo hàm số vx = 0,3sin α (m/s) (Hình 11). Bài 5 trang 33 Toán 11 Tập 1

Bài 6 trang 33 Toán 11 Tập 1
Khoảng cách từ tâm một guồng nước đến mặt nước và bán kính của guồng đều bằng 3m. Xét gàu G của guồng. Ban đầu gàu G nằm ở vị trí A (Hình 12). Bài 6 trang 33 Toán 11 Tập 1

Bài 7 trang 33 Toán 11 Tập 1
Trong Hình 13, một chiếc máy bay A bay ở độ cao 500m theo một đường thẳng đi ngang qua phía trên trạm quan sát T ở mặt đất. Hình chiếu vuông góc của A lên mặt đất là H, α là góc lượng giác (Tx, TA) (0 < α < π). Bài 7 trang 33 Toán 11 Tập 1

Hoạt động khởi động trang 25 Toán 11 Tập 1
Vì sao mặt cắt của sóng nước trên mặt hồ được gọi là có dạng hình sin?

Hoạt động khám phá 1 trang 25 Toán 11 Tập 1
Cho số thực t và M là điểm biểu diễn của góc lượng giác có số đo t rad trên đường tròn lượng giác, hãy giải thích vì sao xác định duy nhất.
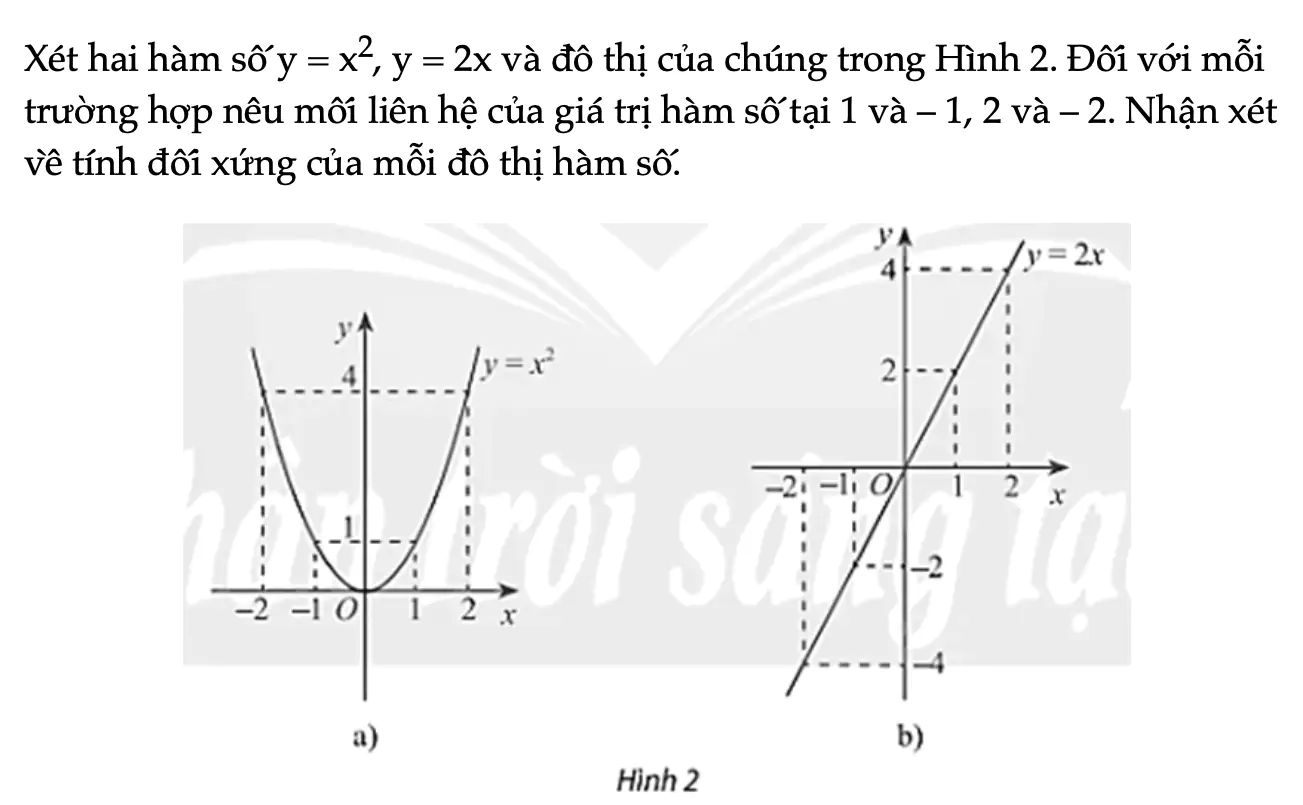
Hoạt động khám phá 2 trang 26 Toán 11 Tập 1
Xét hai hàm số y = x2, y = 2x và đồ thị của chúng trong Hình 2. Đối với mỗi trường hợp nêu mối liên hệ của giá trị hàm số tại 1 và – 1, 2 và – 2. Nhận xét về tính đối xứng của mỗi đồ thị hàm số.
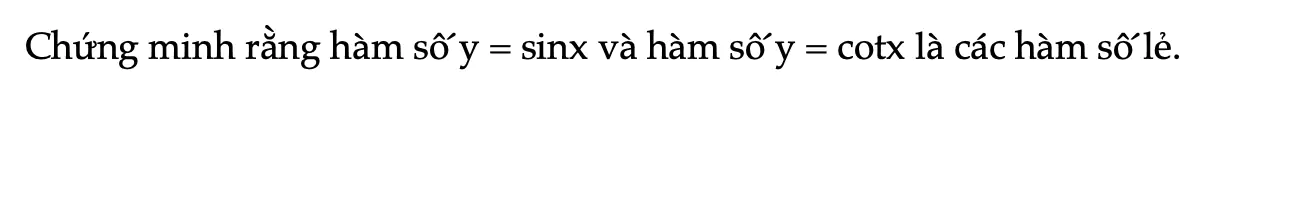
Thực hành 1 trang 27 Toán 11 Tập 1
Chứng minh rằng hàm số y = sinx và hàm số y = cotx là các hàm số lẻ.
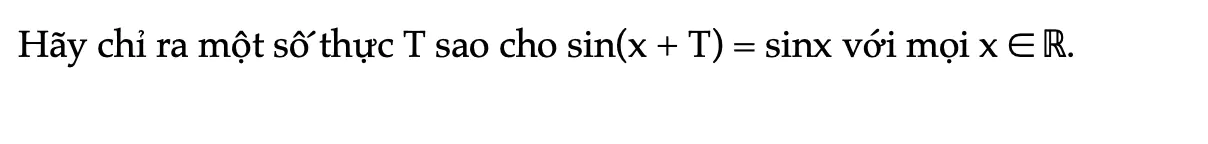
Hoạt động khám phá 3 trang 27 Toán 11 Tập 1
Hãy chỉ ra một số thực T sao cho sin(x + T) = sinx với mọi x ∈ℝ.
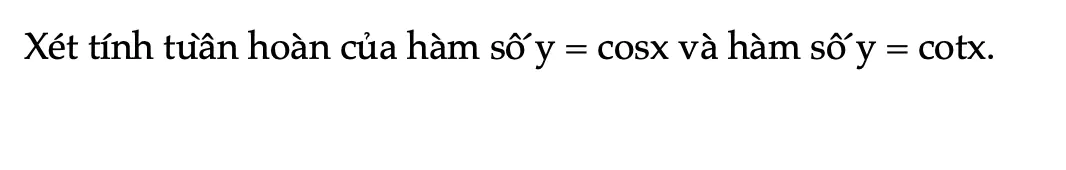
Thực hành 2 trang 27 Toán 11 Tập 1
Xét tính tuần hoàn của hàm số y = cosx và hàm số y = cotx.

Hoạt động khám phá 4 trang 28 Toán 11 Tập 1
Hoàn thành bảng giá trị sau đây và xác định các điểm tương ứng trên mặt phẳng tọa độ.
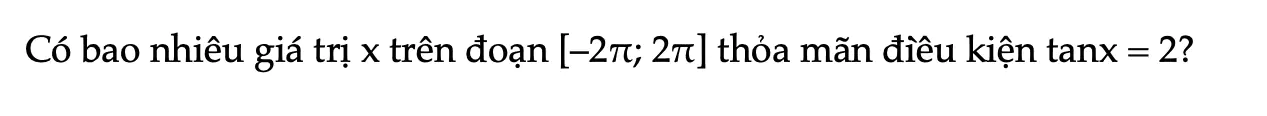
Thực hành 4 trang 32 Toán 11 Tập 1
Có bao nhiêu giá trị x trên đoạn [–2π; 2π] thỏa mãn điều kiện tanx = 2?
Giải bài tập Bài 5: Phương trình lượng giác cơ bản

Bài 1 trang 40 Toán 11 Tập 1
Giải các phương trình lượng giác sau. Bài 1 trang 40 Toán 11 Tập 1

Bài 2 trang 40 Toán 11 Tập 1
Giải các phương trình lượng giác sau. Bài 2 trang 40 Toán 11 Tập 1

Bài 3 trang 41 Toán 11 Tập 1
Giải các phương trình lượng giác sau. Bài 3 trang 41 Toán 11 Tập 1

Bài 4 trang 41 Toán 11 Tập 1
Giải các phương trình lượng giác sau. Bài 4 trang 41 Toán 11 Tập 1
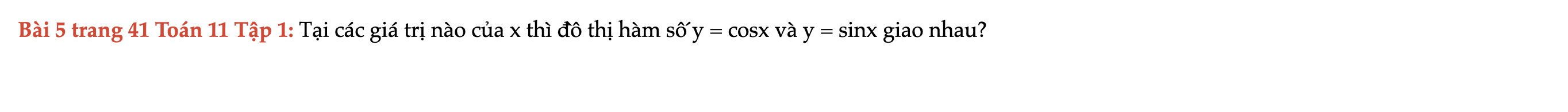
Bài 5 trang 41 Toán 11 Tập 1
Tại các giá trị nào của x thì đồ thị hàm số y = cosx và y = sinx giao nhau. Bài 5 trang 41 Toán 11 Tập 1

Bài 6 trang 41 Toán 11 Tập 1
Trong Hình 9, khi được kéo ra khỏi vị trí cân bằng ở điểm O và buông tay, lực đàn hồi của lò xo khiến vật A gắn ở đầu của lò xo dao động quanh O. Bài 6 trang 41 Toán 11 Tập 1

Bài 7 trang 41 Toán 11 Tập 1
Trong Hình 10, ngọn đèn hải đăng H cách bờ biển yy’ một khoảng HO = 1km. Bài 7 trang 41 Toán 11 Tập 1

Hoạt động khởi động trang 34 Toán 11 Tập 1
Trong hình bên, khi bàn đạp xe đạp quay, bóng M của đầu trục quay dao động trên mặt đất quanh điểm O theo phương trình s = 17cos5πt với s (cm) là tọa độ của điểm M trên trục Ox và t (giây) là thời gian bàn đạp quay.

Hoạt động khám phá 1 trang 34 Toán 11 Tập 1
Xác định và so sánh tập nghiệm của các phương trình sau.
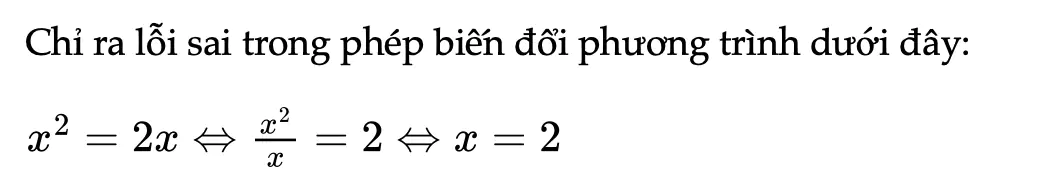
Thực hành 1 trang 35 Toán 11 Tập 1
Chỉ ra lỗi sai trong phép biến đổi phương trình dưới đây.
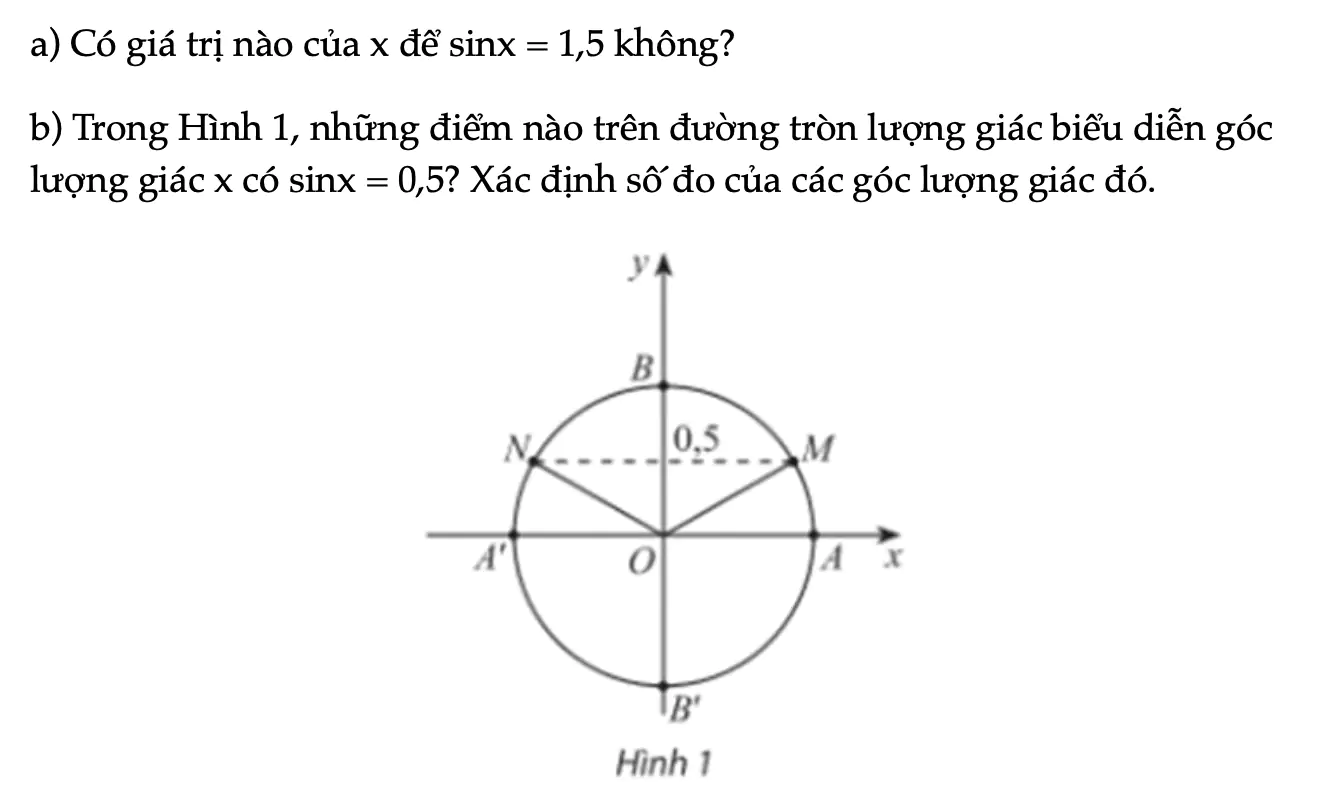
Hoạt động khám phá 2 trang 35 Toán 11 Tập 1
a) Có giá trị nào của x để sinx = 1,5 không? b) Trong Hình 1, những điểm nào trên đường tròn lượng giác biểu diễn góc lượng giác x có sinx = 0,5? Xác định số đo của các góc lượng giác đó.

Thực hành 2 trang 36 Toán 11 Tập 1
Giải các phương trình sau.
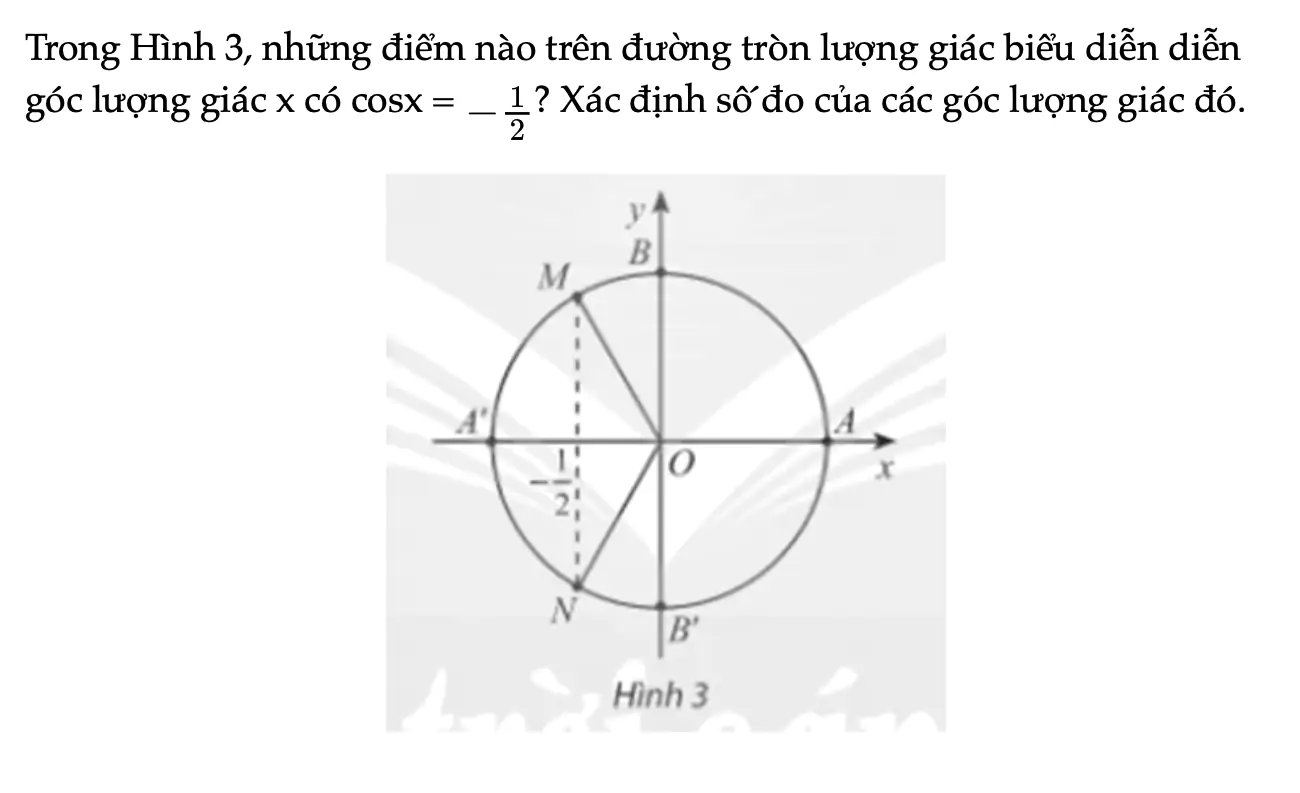
Hoạt động khám phá 3 trang 36 Toán 11 Tập 1
Trong Hình 3, những điểm nào trên đường tròn lượng giác biểu diễn diễn góc lượng giác x có cosx = −1/2 ? Xác định số đo của các góc lượng giác đó.

Thực hành 3 trang 37 Toán 11 Tập 1
Giải các phương trình sau.

Hoạt động khám phá 4 trang 37 Toán 11 Tập 1
Trong mặt phẳng tọa độ Oxy, cho T là điểm trên trục tang có tọa độ là (1; √3) (Hình 5). Những điểm nào trên đường tròn lượng giác biểu diễn góc lượng giác x có tanx = √3? Xác định số đo của các góc lượng giác đó.

Thực hành 4 trang 38 Toán 11 Tập 1
Giải các phương trình sau: a) tanx = 0; b) tan(30° – 3x) = tan75°.
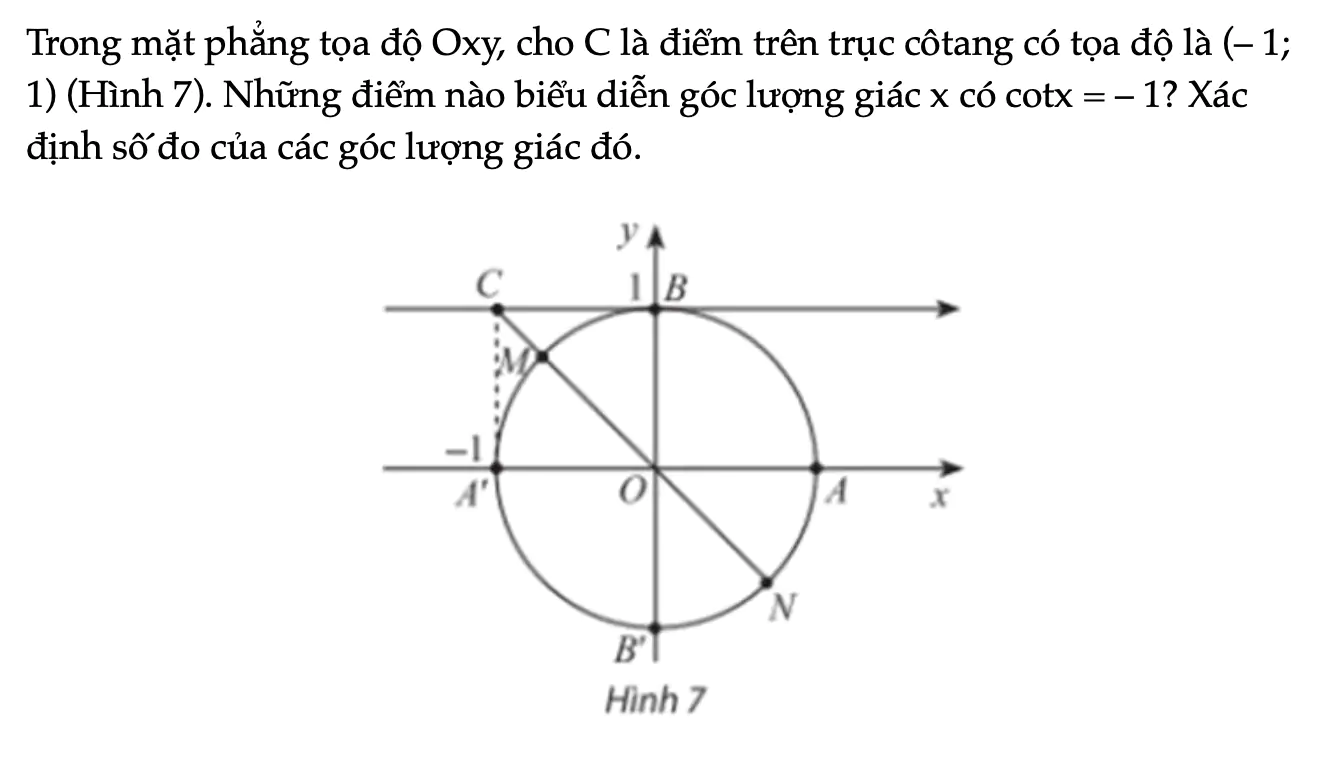
Hoạt động khám phá 5 trang 38 Toán 11 Tập 1
Trong mặt phẳng tọa độ Oxy, cho C là điểm trên trục côtang có tọa độ là (– 1; 1) (Hình 7). Những điểm nào biểu diễn góc lượng giác x có cotx = – 1? Xác định số đo của các góc lượng giác đó.

Thực hành 5 trang 39 Toán 11 Tập 1
Giải các phương trình sau.

Thực hành 6 trang 40 Toán 11 Tập 1
Sử dụng máy tính cầm tay để giải các phương trình sau.

Vận dụng trang 40 Toán 11 Tập 1
Quay lại bài toán khởi động, phương trình chuyển động của bóng đầu trục bàn đạp là x = 17cos5πt (cm) với t được đo bằng giây. Xác định các thời điểm t mà tại đó độ dài bóng |x| bằng 10 cm. Làm tròn kết quả đến hàng phần mười.
Giải bài tập Bài tập cuối chương 1

Bài 1 trang 42 Toán 11 Tập 1
Bài 1 trang 42 Toán 11 Tập 1

Bài 2 trang 42 Toán 11 Tập 1
Trong trường hợp nào dưới đây cosα = cosβ và sinα = – sinβ. Bài 2 trang 42 Toán 11 Tập 1

Bài 3 trang 42 Toán 11 Tập 1
Khẳng định nào sau đây đúng. Bài 3 trang 42 Toán 11 Tập 1
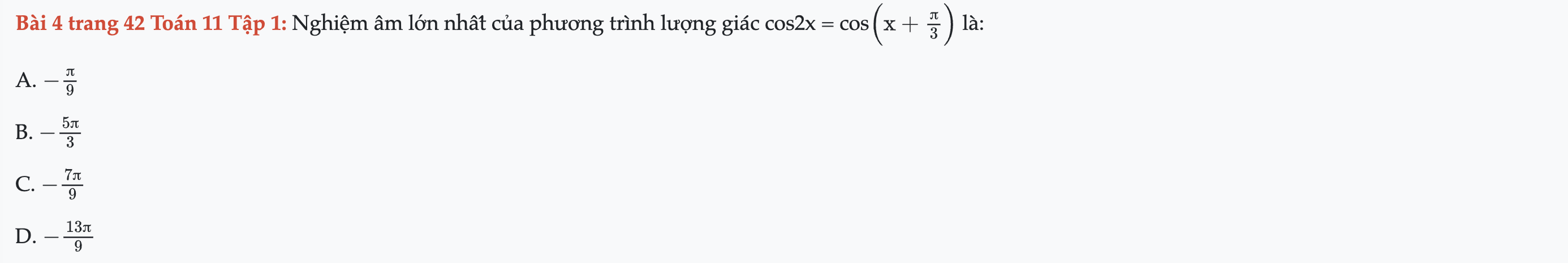
Bài 4 trang 42 Toán 11 Tập 1
Nghiệm âm lớn nhất của phương trình lượng giác. Bài 4 trang 42 Toán 11 Tập 1

Bài 5 trang 42 Toán 11 Tập 1
Nghiệm âm lớn nhất của phương trình lượng giác (-π/2; 7π/3). Bài 5 trang 42 Toán 11 Tập 1

Bài 6 trang 42 Toán 11 Tập 1
Nhiệt độ ngoài trời ở một thành phố vào các thời điểm khác nhau trong ngày có thể được mô phỏng bởi công thức, với h được tính bằng độ C và t là thời gian trong ngày tính bằng giờ. Bài 6 trang 42 Toán 11 Tập 1

Bài 7 trang 42 Toán 11 Tập 1
Một chiếc quạt trần năm cánh quay với tốc độ 45 vòng trong một phút. Chọn chiều quay của quạt là chiều thuận. Sau 3 giây, quạt quay được một góc có số đo bao nhiêu radian. Bài 7 trang 42 Toán 11 Tập 1

Bài 8 trang 42 Toán 11 Tập 1
Bài 8 trang 42 Toán 11 Tập 1

Bài 9 trang 42 Toán 11 Tập 1
Chứng minh đẳng thức lượng giác. Bài 9 trang 42 Toán 11 Tập 1
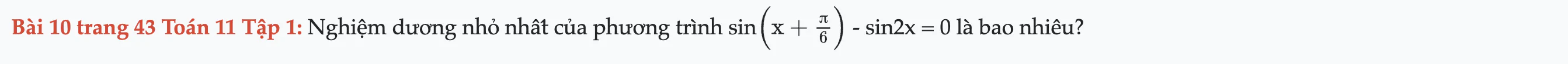
Bài 10 trang 43 Toán 11 Tập 1
Tìm nghiệm dương nhỏ nhất của phương trình. Bài 10 trang 43 Toán 11 Tập 1

Bài 11 trang 43 Toán 11 Tập 1
Giải các phương trình sau. Bài 11 trang 43 Toán 11 Tập 1

Bài 12 trang 43 Toán 11 Tập 1
Độ sâu h(m) của mực nước ở một cảng biển vào thời điểm t (giờ) sau khi thủy triều lên lần đầu tiên trong ngày được tính xấp xỉ bởi công thức h(t) = 0,8cos0,5t + 4. Bài 12 trang 43 Toán 11 Tập 1

Bài 13 trang 43 Toán 11 Tập 1
Cho vận tốc v (cm/s) của một con lắc đơn theo thời gian t (giây) được cho bởi công thức. Bài 13 trang 43 Toán 11 Tập 1

Bài 14 trang 43 Toán 11 Tập 1
Trong Hình 1, cây xanh AB nằm ở trên đường xích đạo được trồng vuông góc với mặt đất và có chiều cao 5m. Bóng của cây là BE. Vào nghày xuân phân và hạ phân, điểm E di chuyển trên đường thẳng Bx. Bài 14 trang 43 Toán 11 Tập 1