Giải bài tập Toán 11 Chương 7: Đạo hàm | Chân trời sáng tạo
Hướng dẫn giải Chương 7: Đạo hàm
Giải bài tập Bài 1: Đạo hàm
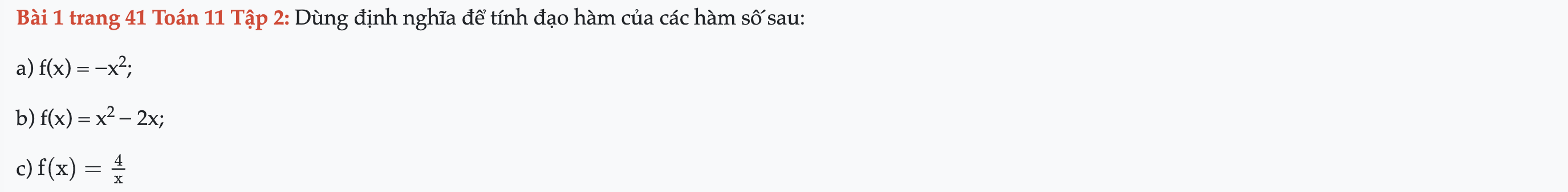
Bài 1 trang 41 Toán 11 Tập 2
Dùng định nghĩa để tính đạo hàm của các hàm số sau. Bài 1 trang 41 Toán 11 Tập 2
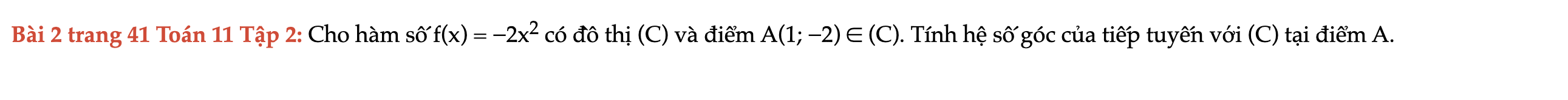
Bài 2 trang 41 Toán 11 Tập 2
Cho hàm số f(x) = −2x%2 có đồ thị (C) và điểm A(1; −2) ∈ (C). Tính hệ số góc của tiếp tuyến với (C) tại điểm A. Bài 2 trang 41 Toán 11 Tập 2
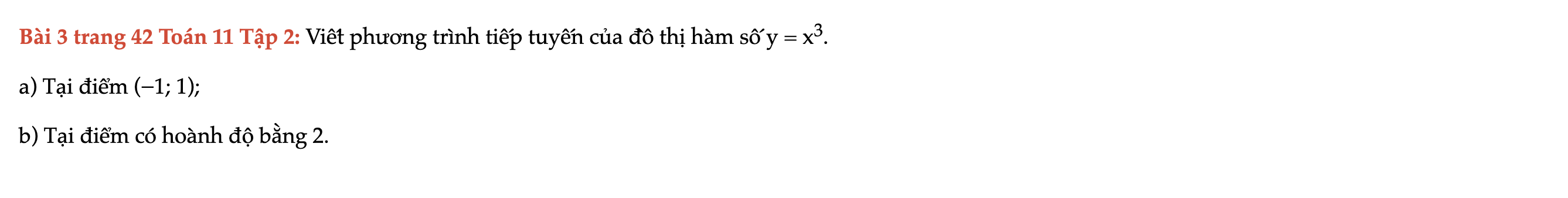
Bài 3 trang 42 Toán 11 Tập 2
Viết phương trình tiếp tuyến của đồ thị hàm số y = x^3. Tại điểm (−1; 1); tại điểm có hoành độ bằng 2. Bài 3 trang 42 Toán 11 Tập 2
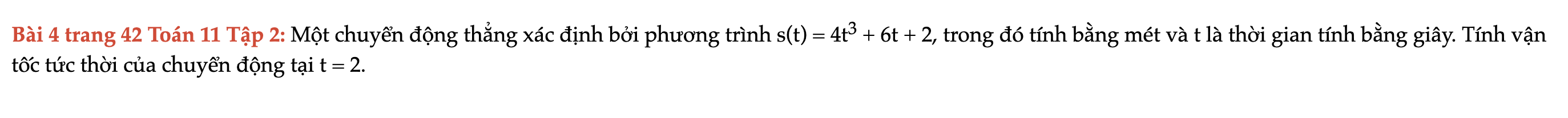
Bài 4 trang 42 Toán 11 Tập 2
Một chuyển động thẳng xác định bởi phương trình s(t) = 4t^3 + 6t + 2, trong đó tính bằng mét và t là thời gian tính bằng giây. Tính vận tốc tức thời của chuyển động tại t = 2. Bài 4 trang 42 Toán 11 Tập 2

Bài 5 trang 42 Toán 11 Tập 2
Một người gửi tiết kiệm khoản tiền 10 triệu đồng vào một ngân hàng với lãi suất 5%/năm. Tính tổng số tiền vốn và lãi mà người đó nhận được sau một năm, nếu tiền lãi được tính theo thể thức lãi kép với kì hạn 6 tháng. Bài 5 trang 42 Toán 11 Tập 2
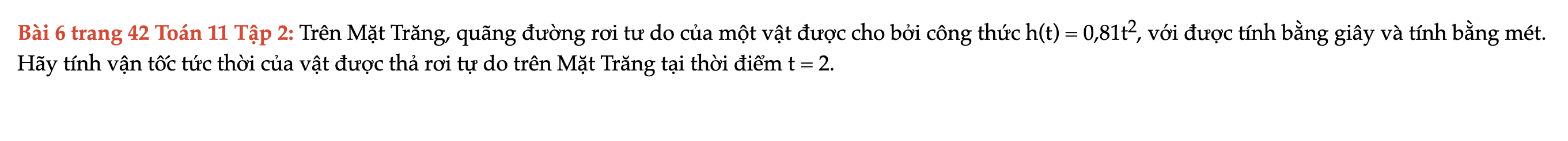
Bài 6 trang 42 Toán 11 Tập 2
Trên Mặt Trăng, quãng đường rơi tư do của một vật được cho bởi công thức h(t) = 0,81t^2, với được tính bằng giây và tính bằng mét. Hãy tính vận tốc tức thời của vật được thả rơi tự do trên Mặt Trăng tại thời điểm t = 2. Bài 6 trang 42 Toán 11 Tập 2

Hoạt động khởi động trang 36 Toán 11 Tập 2
Đạo hàm là một khái niệm quan trọng của Giải tích. Đạo hàm cho biết “tốc độ thay đổi” của hàm số theo biến số. Trong chương này, chúng ta sẽ tìm hiểu về đạo hàm, ý nghĩa hình học của đạo hàm, các quy tắc tính đạo hàm.

Hoạt động khởi động trang 37 Toán 11 Tập 2
Giữa tốc độ của xe và quãng đường mà xe đi được có mối liên hệ như thế nào? Nếu biết quãng đường s(t) tại mọi điểm t thì có thể tính được tốc độ của xe tại mỗi thời điểm không?

Hoạt động khám phá 1 trang 37 Toán 11 Tập 2
Quãng đường rơi tự do của một vật được biểu diễn bởi công thức s(t) = 4,9t2 với t là thời gian tính bằng giây và s tính bằng mét.
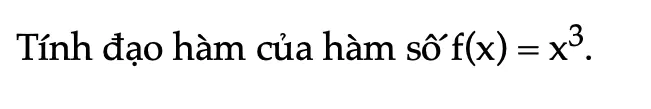
Thực hành 1 trang 39 Toán 11 Tập 2
Tính đạo hàm của hàm số f(x) = x3.

Vận dụng trang 39 Toán 11 Tập 2
Với tình huống trong Hoạt động khám phá 1, hãy tính vận tốc tức thời của chuyển động lúc t = 2.

Hoạt động khám phá 2 trang 39 Toán 11 Tập 2
Cho hàm số y = f(x) đồ thị (C) và điểm M thuộc (C). a) Vẽ (C) và tính f' (1). b) Vẽ đường thẳng d đi qua điểm M và có hệ số góc bằng f' (1). Nêu nhận xét về vị trí tương đối giữa d và (C).
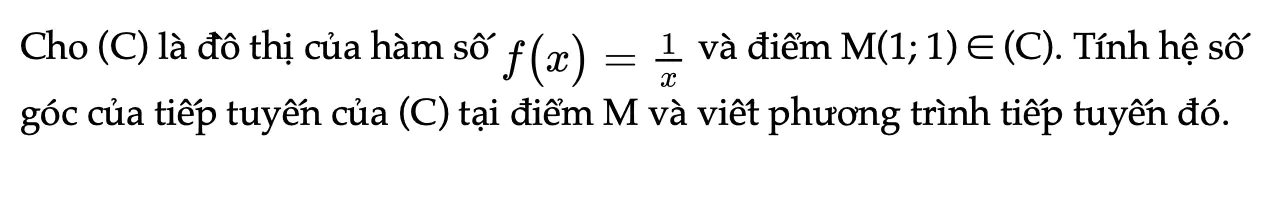
Thực hành 2 trang 40 Toán 11 Tập 2
Cho (C) là đồ thị của hàm số f(x) và điểm M(1; 1) ∈ (C). Tính hệ số góc của tiếp tuyến của (C) tại điểm M và viết phương trình tiếp tuyến đó.

Hoạt động khám phá 3 trang 40 Toán 11 Tập 2
Một người gửi tiết kiệm khoản tiền A triệu đồng (gọi là vốn) với lãi suất r/năm theo thể thức lãi kép (tiền lãi sau mỗi kì hạn được cộng gộp vào vốn). Tính tổng số tiền vốn và lãi sau một năm của người gửi nếu kì hạn là?

Thực hành 3 trang 41 Toán 11 Tập 2
Một người gửi tiết kiệm khoản tiền 5 triệu đồng vào ngân hàng với lãi suất 4% năm và theo thể thức lãi kép liên tục. Tính tổng số tiền vốn và lãi mà người đó nhận được sau: a) 1 ngày. b) 30 ngày. (Luôn coi một năm có 365 ngày.)
Giải bài tập Bài 2: Các quy tắc tính đạo hàm
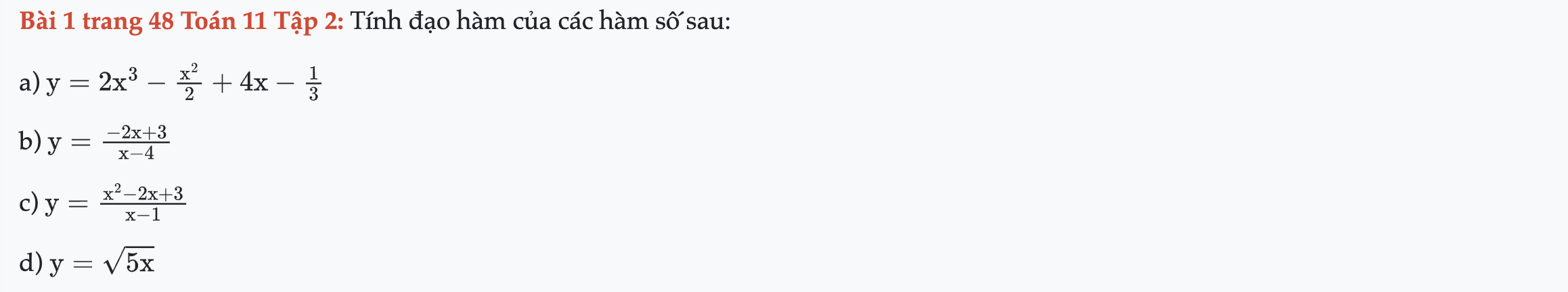
Bài 1 trang 48 Toán 11 Tập 2
Tính đạo hàm của các hàm số sau. Bài 1 trang 48 Toán 11 Tập 2

Bài 2 trang 49 Toán 11 Tập 2
Tính đạo hàm của các hàm số sau. Bài 2 trang 49 Toán 11 Tập 2

Bài 3 trang 49 Toán 11 Tập 2
Tính đạo hàm của các hàm số sau. Bài 3 trang 49 Toán 11 Tập 2

Bài 4 trang 49 Toán 11 Tập 2
Tính đạo hàm cấp hai của các hàm số sau. Bài 4 trang 49 Toán 11 Tập 2

Bài 5 trang 49 Toán 11 Tập 2
Cân nặng trung bình của một bé gái trong độ tuổi từ 0 đến 36 tháng có thể được tính gần đúng bởi hàm số w(t), trong đó t được tính bằng tháng và w được tính bằng pound. Bài 5 trang 49 Toán 11 Tập 2

Bài 6 trang 49 Toán 11 Tập 2
Một công ty xác định rằng tổng chi phí của họ, tính theo nghìn đô-la, để sản xuất x mặt hàng là C(x) và công ty lên kế hoạch nâng sản lượng trong t tháng kể từ nay theo hàm số x(t) = 20t + 40. Bài 6 trang 49 Toán 11 Tập 2

Bài 7 trang 49 Toán 11 Tập 2
Trên Mặt Trăng, quãng đường rơi tự do của một vật được cho bởi công thức s(t) = 0,81t^2, trong đó t là thời gian được tính bằng giây và s tính bằng mét. Một vật được thả rơi từ độ cao 200 m phía trên Mặt Trăng. Bài 7 trang 49 Toán 11 Tập 2

Hoạt động khám phá 3 trang 44 Toán 11 Tập 2
Cho biểu thức sau. Dùng định nghĩa tính đạo hàm của hàm số y = sinx.
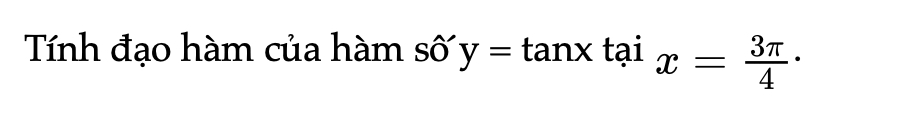
Thực hành 4 trang 44 Toán 11 Tập 2
Tính đạo hàm của hàm số y = tanx tại x=3π/4.
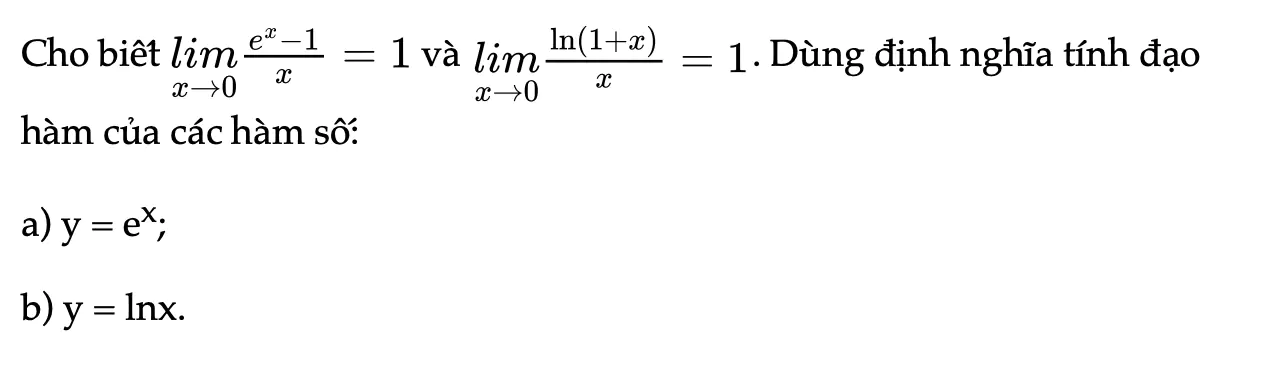
Hoạt động khám phá 4 trang 44 Toán 11 Tập 2
Dùng định nghĩa tính đạo hàm của các hàm số: a) y = ex; b) y = lnx.
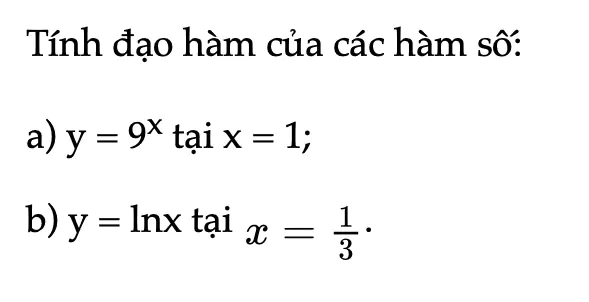
Thực hành 5 trang 44 Toán 11 Tập 2
Tính đạo hàm của các hàm số.

Hoạt động khám phá 5 trang 45 Toán 11 Tập 2
Cho f(x) và g(x) là hai hàm số có đạo hàm tại x0. Xét hàm số h(x) = f(x) + g(x). Chọn biểu thức thích hợp thay cho chỗ chấm để tìm h'(x0).

Thực hành 6 trang 46 Toán 11 Tập 2
Tính đạo hàm của các hàm số.

Hoạt động khám phá 6 trang 46 Toán 11 Tập 2
Cho hàm số u = sinx và hàm số y = u2. a) Tính y theo x. b) Tính y'x (đạo hàm của y theo biến x), y'u (đạo hàm của y theo biến u) và u'x (đạo hàm của u theo biến x) rồi so sánh y'x với y'u×u'x.
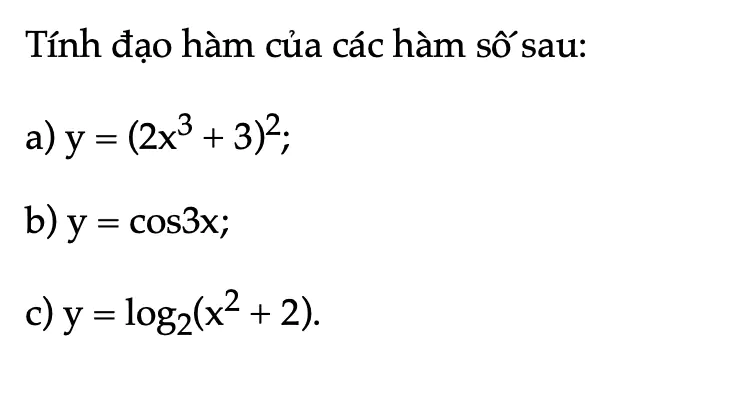
Thực hành 7 trang 47 Toán 11 Tập 2
Tính đạo hàm của các hàm số sau.

Hoạt động khám phá 7 trang 47 Toán 11 Tập 2
Một chuyển động thẳng xác định bởi phương trình s(t) = 2t3 + 4t + 1, trong đó s tính bằng mét và t là thời gian tính bằng giây. a) Tính vận tốc tức thời v(t) tại thời điểm t. b) Tính gia tốc của chuyển động tại thời điểm t = 2.

Thực hành 8 trang 48 Toán 11 Tập 2
Tính đạo hàm cấp hai của các hàm số sau: a) y = x2 – x; b) y = cosx.

Vận dụng trang 48 Toán 11 Tập 2
Một hòn sỏi rơi tự do có quãng đường rơi tính theo thời gian t là s(t) = 4,9t2 , trong đó s tính bằng mét và t tính bằng giây. Tính gia tốc rơi của hòn sỏi lúc t = 3.
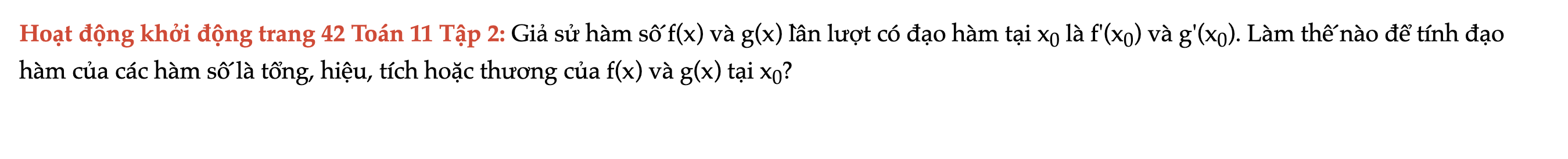
Hoạt động khởi động trang 42 Toán 11 Tập 2
Giả sử hàm số f(x) và g(x) lần lượt có đạo hàm tại x0 là f'(x0) và g'(x0). Làm thế nào để tính đạo hàm của các hàm số là tổng, hiệu, tích hoặc thương của f(x) và g(x) tại x0? Hoạt động khởi động trang 42 Toán 11 Tập 2

Hoạt động khám phá 1 trang 42 Toán 11 Tập 2
Dùng định nghĩa tính đạo hàm của hàm số y = x tại điểm x = x0. hắc lại đạo hàm của các hàm số y = x2; y = x3 đã tìm được ở bài học trước. Từ đó, dự đoán đạo hàm của hàm số y = xn với n ∈ ℕ*. Hoạt động khám phá 1 trang 42 Toán 11 Tập 2
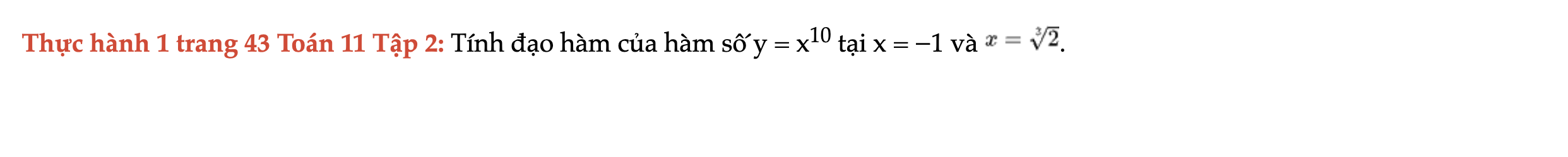
Thực hành 1 trang 43 Toán 11 Tập 2
Tính đạo hàm của hàm số sau. Thực hành 1 trang 43 Toán 11 Tập 2

Hoạt động khám phá 2 trang 43 Toán 11 Tập 2
Dùng định nghĩa, tính đạo hàm của hàm số sau tại điểm x = x0 với x0 > 0. Hoạt động khám phá 2 trang 43 Toán 11 Tập 2

Thực hành 2 trang 43 Toán 11 Tập 2
Viết phương trình tiếp tuyến của đồ thị hàm số sau tại điểm có hoành độ bằng 4. Thực hành 2 trang 43 Toán 11 Tập 2

Thực hành 3 trang 43 Toán 11 Tập 2
Tìm đạo hàm của các hàm số sau. Thực hành 3 trang 43 Toán 11 Tập 2
Giải bài tập Bài tập cuối chương 7

Bài 1 trang 51 Toán 11 Tập 2
Cho hàm số y, tiếp tuyến với đồ thị của hàm số tại điểm M(−1; −4) có hệ số góc bằng. Bài 1 trang 51 Toán 11 Tập 2
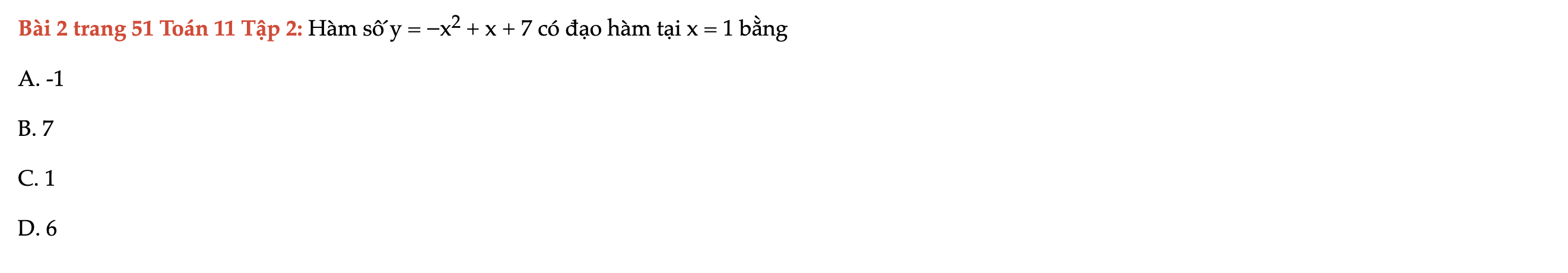
Bài 2 trang 51 Toán 11 Tập 2
Hàm số y có đạo hàm tại x = 1 bằng. Bài 2 trang 51 Toán 11 Tập 2

Bài 3 trang 51 Toán 11 Tập 2
Cho hai hàm số f(x) và g(x). Bất phương trình f'(x) > g'(x) có tập nghiệm là. Bài 3 trang 51 Toán 11 Tập 2

Bài 4 trang 51 Toán 11 Tập 2
Hàm số y có đạo hàm là. Bài 4 trang 51 Toán 11 Tập 2
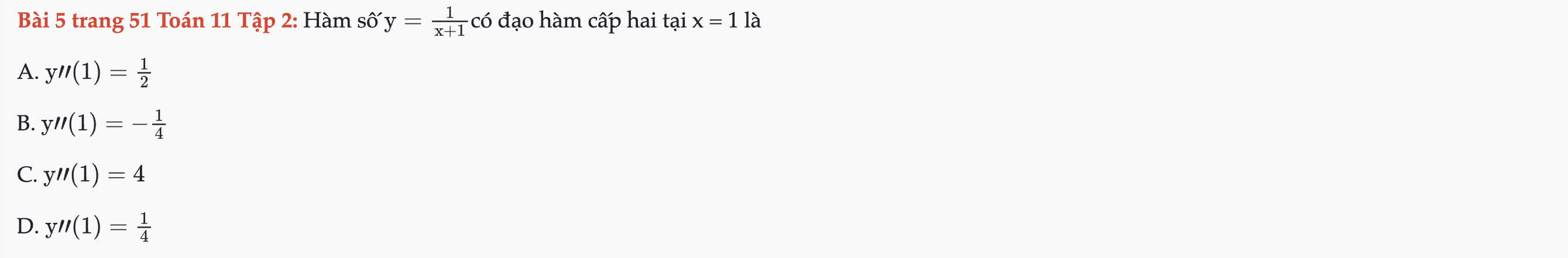
Bài 5 trang 51 Toán 11 Tập 2
Hàm số y có đạo hàm cấp hai tại x = 1 là. Bài 5 trang 51 Toán 11 Tập 2

Bài 6 trang 51 Toán 11 Tập 2
Cho hàm số f(x) = x^2 – 2x + 3 có đồ thị (C) và điểm M(−1; 6) ∈ (C). Viết phương trình tiếp tuyến với (C) tại điểm M. Bài 6 trang 51 Toán 11 Tập 2

Bài 7 trang 51 Toán 11 Tập 2
Tính đạo hàm của các hàm số sau. Bài 7 trang 51 Toán 11 Tập 2
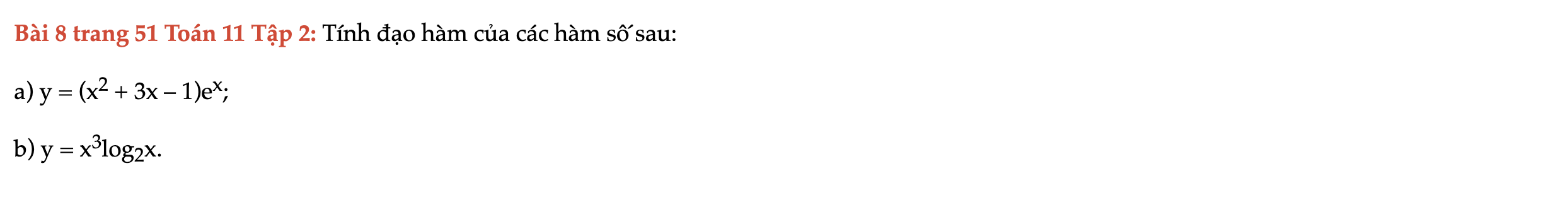
Bài 8 trang 51 Toán 11 Tập 2
Tính đạo hàm của các hàm số sau. Bài 8 trang 51 Toán 11 Tập 2

Bài 9 trang 51 Toán 11 Tập 2
Tính đạo hàm của các hàm số sau. Bài 9 trang 51 Toán 11 Tập 2

Bài 10 trang 51 Toán 11 Tập 2
Tính đạo hàm cấp hai của các hàm số sau. Bài 10 trang 51 Toán 11 Tập 2

Bài 11 trang 51 Toán 11 Tập 2
Một viên sỏi rơi từ độ cao 44,1 m thì quãng đường rơi được biểu diễn bởi công thức s(t) = 4,9t^2, trong đó t là thời gian tính bằng giây và s tính bằng mét. Bài 11 trang 51 Toán 11 Tập 2

Bài 12 trang 51 Toán 11 Tập 2
Một vật chuyển động trên đường thẳng được xác định bởi công thức s(t) = 2t^3 + 4t + 1, trong đó t là thời gian tính bằng giây và s tính bằng mét. Tính vận tốc và gia tốc của vật khi t = 1. Bài 12 trang 51 Toán 11 Tập 2

Bài 13 trang 52 Toán 11 Tập 2
Dân số P (tính theo nghìn người) của một thành phố nhỏ được cho bởi công thức P(t), trong đó t là thời gian được tính bằng năm. Tìm tốc độ tăng dân số tại thời điểm t = 12. Bài 13 trang 52 Toán 11 Tập 2

Bài 14 trang 52 Toán 11 Tập 2
Hàm số S(r) có thể được sử dụng để xác định sức cản S của dòng máu trong mạch máu có bán kính r (tính theo milimet) (theo Bách khoa toàn thư Y học "Harrison's internal medicine 21st edition"). Bài 14 trang 52 Toán 11 Tập 2

Bài 15 trang 52 Toán 11 Tập 2
Bệnh được cho bởi công thức T(t), trong đó T là nhiệt độ (tính theo đơn vị đo nhiệt độ Fahrenheit) tại thời điểm t (tính theo ngày). Tìm tốc độ thay đổi của nhiệt độ ở thời điểm t = 1,5. Bài 15 trang 52 Toán 11 Tập 2

Bài 16 trang 52 Toán 11 Tập 2
Hàm số R(v) có thể được sử dụng để xác định nhịp tim R của một người mà tim của người đó có thể đẩy đi được 6 000ml máu trên mỗi phút và v ml máu trên mỗi nhịp đập. Bài 16 trang 52 Toán 11 Tập 2