Giải bài tập Bài 1 trang 51 Toán 11 Tập 2 | Toán 11 - Chân trời sáng tạo
Hướng dẫn giải chi tiết từng bước bài tập Bài 1 trang 51 Toán 11 Tập 2. Bài tập cuối chương 7. Toán 11 - Chân trời sáng tạo
Đề bài:
Bài 1 trang 51 Toán 11 Tập 2: Cho hàm số y = x3 – 3x2. Tiếp tuyến với đồ thị của hàm số tại điểm M(−1; −4) có hệ số góc bằng
A. -3
B. 9
C. -9
D. 72
Đáp án và cách giải chi tiết:
Đáp án đúng là: B
Ta có y' = (x3 – 3x2)' = 3x2 – 6x.
Tiếp tuyến với đồ thị của hàm số tại điểm M(−1; −4) có hệ số góc là:
k = y'(−1) = 3*(−1)2 – 6*(−1) = 9.
Vậy k = 9 là hệ số góc cần tìm.
Nguồn: loigiaitoan.com
Tổng số đánh giá: 0
Xếp hạng: 5 / 5 sao
Các công thức liên quan:
Công thức đạo hàm
Bài tập liên quan:
Bài 16 trang 52 Toán 11 Tập 2
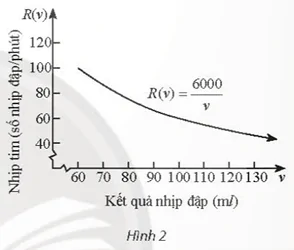
Bài 16 trang 52 Toán 11 Tập 2: Hàm số
Bài 15 trang 52 Toán 11 Tập 2
Bài 15 trang 52 Toán 11 Tập 2: Bệnh được cho bởi công thức T(t) = −0,1t2 + 1,2t + 98,6, trong đó T là nhiệt độ (tính theo đơn vị đo nhiệt độ Fahrenheit) tại thời điểm t (tính theo ngày). Tìm tốc độ thay đổi của nhiệt độ ở thời điểm t = 1,5.
(Nguồn:https://www.algebra.com/algebra/homework/Trigonometry-basics/Trigonometry-basics.faq.question.
Bài 14 trang 52 Toán 11 Tập 2
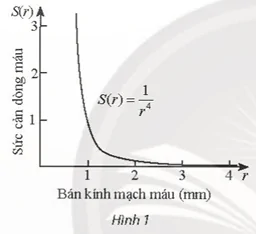
Bài 14 trang 52 Toán 11 Tập 2: Hàm số
Bài 13 trang 52 Toán 11 Tập 2
Bài 13 trang 52 Toán 11 Tập 2: Dân số P (tính theo nghìn người) của một thành phố nhỏ được cho bởi công thức
Bài 12 trang 51 Toán 11 Tập 2
Bài 12 trang 51 Toán 11 Tập 2: Một vật chuyển động trên đường thẳng được xác định bởi công thức s(t) = 2t3 + 4t + 1, trong đó t là thời gian tính bằng giây và s tính bằng mét. Tính vận tốc và gia tốc của vật khi t = 1.
Bài 11 trang 51 Toán 11 Tập 2
Bài 11 trang 51 Toán 11 Tập 2: Một viên sỏi rơi từ độ cao 44,1 m thì quãng đường rơi được biểu diễn bởi công thức s(t) = 4,9t2, trong đó t là thời gian tính bằng giây và s tính bằng mét. Tính:
a) Vận tốc rơi của viên sỏi lúc t = 2;
b) Vận tốc của viên sỏi khi chạm đất.
Bài 10 trang 51 Toán 11 Tập 2
Bài 10 trang 51 Toán 11 Tập 2: Tính đạo hàm cấp hai của các hàm số sau:
a) y = x3 – 4x2 + 2x – 3;
b) y = x2ex.
Bài 8 trang 51 Toán 11 Tập 2
Bài 8 trang 51 Toán 11 Tập 2: Tính đạo hàm của các hàm số sau:
a) y = (x2 + 3x – 1)ex;
b) y = x3log2x.
Bài 7 trang 51 Toán 11 Tập 2
Bài 7 trang 51 Toán 11 Tập 2: Tính đạo hàm của các hàm số sau:
a) y = 3x4 – 7x3 + 3x2 + 1;
b) y = (x2 – x)3;
c)
Bài 6 trang 51 Toán 11 Tập 2
Bài 6 trang 51 Toán 11 Tập 2: Cho hàm số f(x) = x2 – 2x + 3 có đồ thị (C) và điểm M(−1; 6) (C). Viết phương trình tiếp tuyến với (C) tại điểm M.
Bài 5 trang 51 Toán 11 Tập 2
Bài 5 trang 51 Toán 11 Tập 2: Hàm số
A.
B.
C.
D.
Bài 4 trang 51 Toán 11 Tập 2
Bài 4 trang 51 Toán 11 Tập 2: Hàm số
A.
B.
C.
D.
Bài 3 trang 51 Toán 11 Tập 2
Bài 3 trang 51 Toán 11 Tập 2: Cho hai hàm số f(x) = 2x3 – x2 + 3 và
A.
B. (0; 1)
C. [0; 1]
D.
Bài 2 trang 51 Toán 11 Tập 2
Bài 2 trang 51 Toán 11 Tập 2: Hàm số y = −x2 + x + 7 có đạo hàm tại x = 1 bằng
A. -1
B. 7
C. 1
D. 6
Bài 9 trang 51 Toán 11 Tập 2
Bài 9 trang 51 Toán 11 Tập 2: Tính đạo hàm của các hàm số sau:
a) y = tan(ex + 1);
b) 
;
c) y = cot(1 – 2x).