Giải bài tập Toán 11 Chương 4: Đường thẳng và mặt phẳng. Quan hệ song song trong không gian | Chân trời sáng tạo
Hướng dẫn giải chi tiết Chương 4: Đường thẳng và mặt phẳng. Quan hệ song song trong không gian
Giải bài tập Bài 1: Điểm, đường thẳng và mặt phẳng trong không gian

Bài 1 trang 99 Toán 11 Tập 1
Cho hình chóp S.ABCD, gọi O là giao điểm của AC và BD. Lấy M, N lần lượt thuộc các cạnh SA, SC. Bài 1 trang 99 Toán 11 Tập 1

Bài 2 trang 99 Toán 11 Tập 1
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi M là trung điểm của SC. Bài 2 trang 99 Toán 11 Tập 1

Bài 3 trang 99 Toán 11 Tập 1
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi O là giao điểm của AC và BD; M và N lần lượt là trung điểm của SB và SD; P thuộc đoạn SC và không là trung điểm của SC. Bài 3 trang 99 Toán 11 Tập 1

Bài 4 trang 99 Toán 11 Tập 1
Cho tứ diện ABCD. Gọi E, F, G lần lượt là ba điểm trên ba cạnh AB, AC, BD sao cho EF cắt BC tại I (I ≠ C), EG cắt AD tại H (H ≠ D). Bài 4 trang 99 Toán 11 Tập 1

Bài 5 trang 99 Toán 11 Tập 1
Thước laser phát tia laser, khi tia này quay sẽ tạo ra mặt phẳng ánh sáng (Hình 41). Giải thích tại sao các thước kẻ laser lại giúp người thợ xây dựng được đường thẳng trên tường hoặc sàn nhà. Bài 5 trang 99 Toán 11 Tập 1

Hoạt động khởi động trang 88 Toán 11 Tập 1
Môn học Hình học phẳng tìm hiểu tính chất của các hình cùng thuộc một mặt phẳng. Môn học Hình học không gian tìm hiểu tính chất của các hình trong không gian, những hình này có thể chứa những điểm không cùng thuộc 1 mặt phẳng. Hãy phân loại các hình sau

Hoạt động khám phá 1 trang 88 Toán 11 Tập 1
Mặt bàn, mặt bảng cho ta hình ảnh của mặt phẳng. Hãy chỉ thêm các ví dụ khác về hình ảnh một phần của mặt phẳng.
Thực hành 1 trang 89 Toán 11 Tập 1
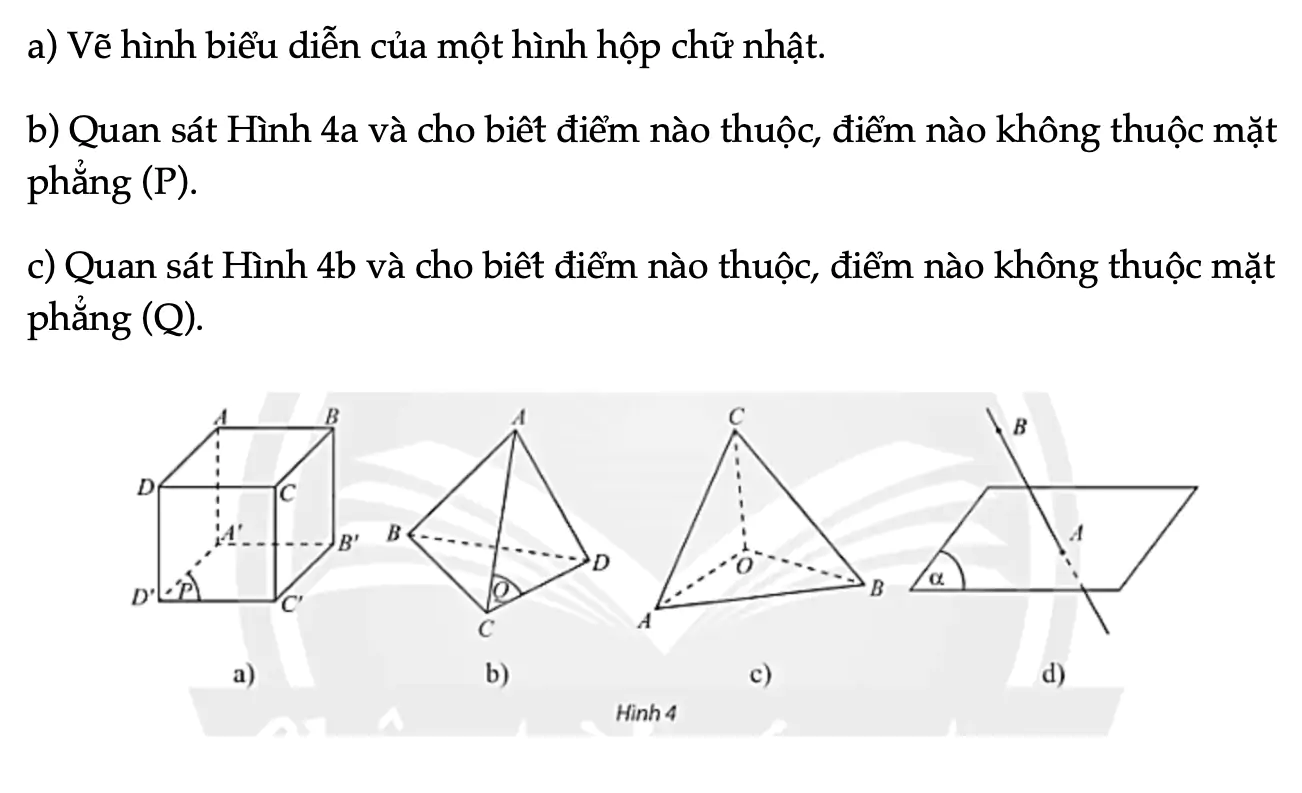
a) Vẽ hình biểu diễn của một hình hộp chữ nhật. b) Quan sát Hình 4a và cho biết điểm nào thuộc, điểm nào không thuộc mặt phẳng (P). c) Quan sát Hình 4b và cho biết điểm nào thuộc, điểm nào không thuộc mặt phẳng (Q).

Hoạt động khám phá 2 trang 89 Toán 11 Tập 1
Quan sát Hình 5 và cho biết muốn gác một cây sào tập nhảy cao, người ta cần dựa nó vào mấy điểm trên hai cọc đỡ.

Thực hành 2 trang 90 Toán 11 Tập 1
Cho bốn điểm A, B, C, D phân biệt, trong đó không có ba điểm nào thẳng hàng. Có bao nhiêu đường thẳng đi qua hai trong bốn điểm đã cho.

Hoạt động khám phá 3 trang 90 Toán 11 Tập 1
Quan sát Hình 7 và cho biết giá đỡ của máy ảnh tiếp đất tại mấy điểm. Tại sao giá đỡ máy ảnh thường có ba chân?

Thực hành 3 trang 90 Toán 11 Tập 1
Có bao nhiêu mặt phẳng đi qua ba đỉnh của tam giác MNP?

Hoạt động khám phá 4 trang 90 Toán 11 Tập 1
Quan sát Hình 10 và cho biết thợ mộc kiểm tra mặt bàn có phẳng hay không bằng một cây thước thẳng như thế nào?

Thực hành 4 trang 91 Toán 11 Tập 1
Cho mặt phẳng (Q) đi qua bốn đỉnh của tứ giác ABCD. Các điểm nằm trên đường chéo của tứ giác ABCD có thuộc mặt phẳng (Q) không? Giải thích.

Hoạt động khám phá 5 trang 91 Toán 11 Tập 1
Quan sát Hình 13 và cho biết bốn đỉnh A, B, C, D của cái bánh giò có cùng nằm trên một mặt phẳng hay không?

Thực hành 5 trang 91 Toán 11 Tập 1
Cho tam giác MNP và cho điểm O không thuộc mặt phẳng chứa ba điểm M, N, P. Tìm các mặt phẳng phân biệt được xác định từ bốn điểm M, N, P, O.

Hoạt động khám phá 6 trang 92 Toán 11 Tập 1
Quan sát Hình 14 và mô tả phần giao nhau của hai bức tường.
Thực hành 6 trang 92 Toán 11 Tập 1
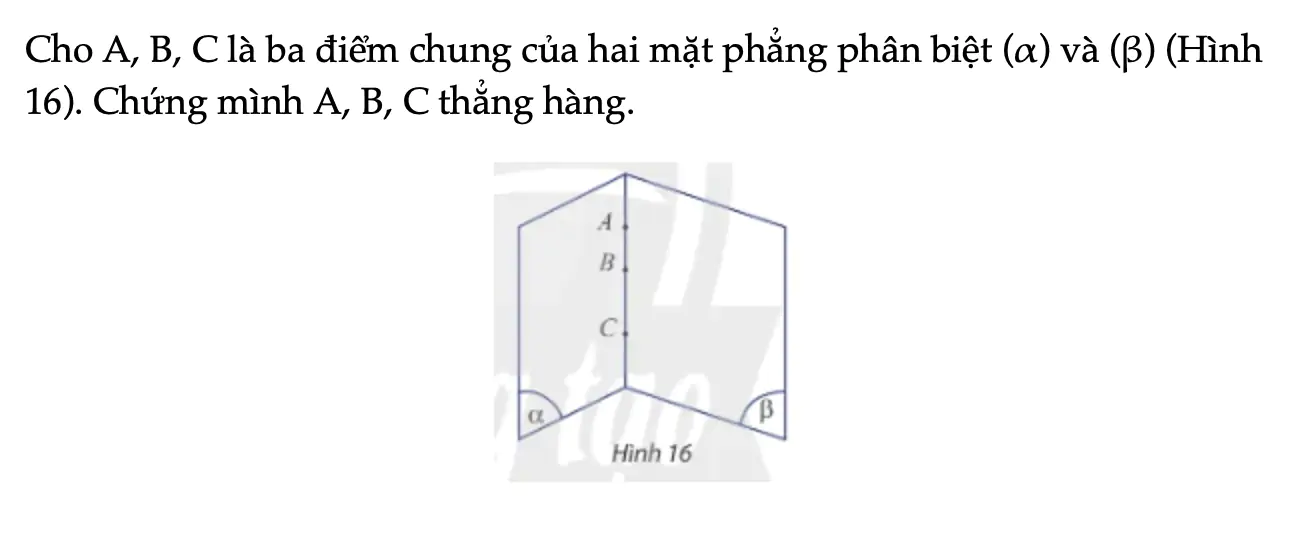
Cho A, B, C là ba điểm chung của hai mặt phẳng phân biệt (α) và (β) (Hình 16). Chứng mình A, B, C thẳng hàng.
Hoạt động khám phá 7 trang 92 Toán 11 Tập 1
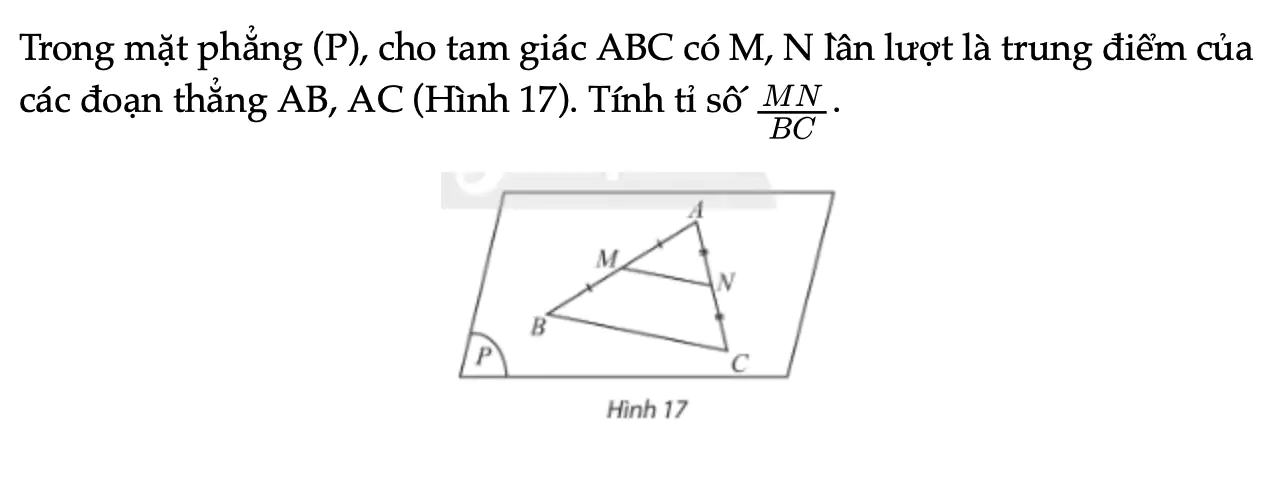
Trong mặt phẳng (P), cho tam giác ABC có M, N lần lượt là trung điểm của các đoạn thẳng AB, AC (Hình 17). Tính tỉ số MN/BC.

Vận dụng 1 trang 93 Toán 11 Tập 1
Tại sao muốn cánh cửa đóng mở được êm thì các điểm gắn bản lề A, B, C của cánh cửa và mặt tường (Hình 19) phải cùng nằm trên một đường thẳng?
Hoạt động khám phá 8 trang 94 Toán 11 Tập 1
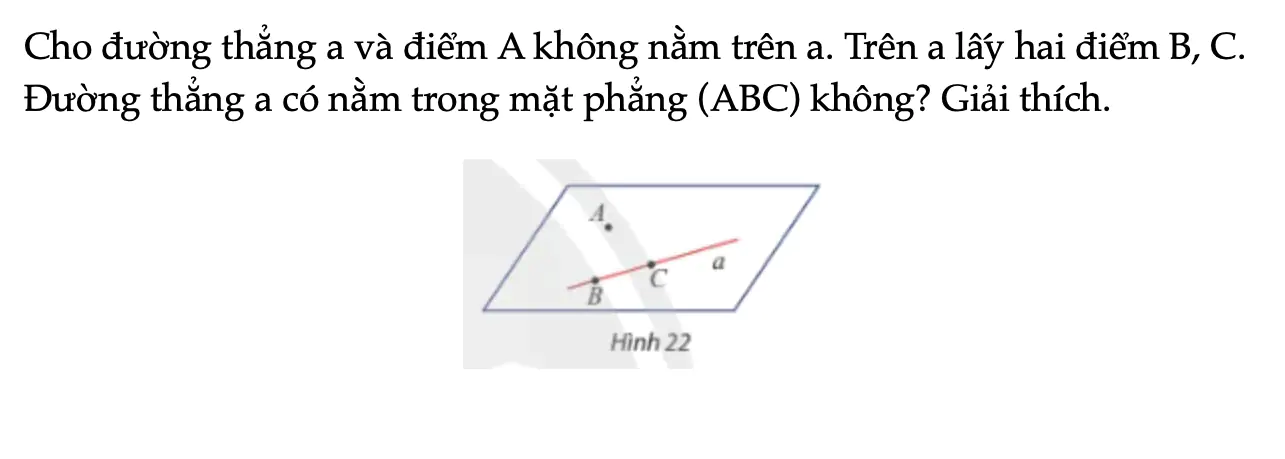
Cho đường thẳng a và điểm A không nằm trên a. Trên a lấy hai điểm B, C. Đường thẳng a có nằm trong mặt phẳng (ABC) không? Giải thích.

Hoạt động khám phá 9 trang 95 Toán 11 Tập 1
Hai đường thẳng phân biệt a và b cắt nhau tại điểm O. Trên a, b lấy lần lượt hai điểm M, N khác O. Gọi (P) là mặt phẳng đi qua ba điểm M, N, O (Hình 25). Mặt phẳng (P) có chứa cả hai đường thẳng a và b không? Giải thích.

Thực hành 7 trang 95 Toán 11 Tập 1
Cho hai đường thẳng a và b cắt nhau tại O và điểm M không thuộc mặt phẳng (a, b). Thực hiện các yêu cầu bài toán.
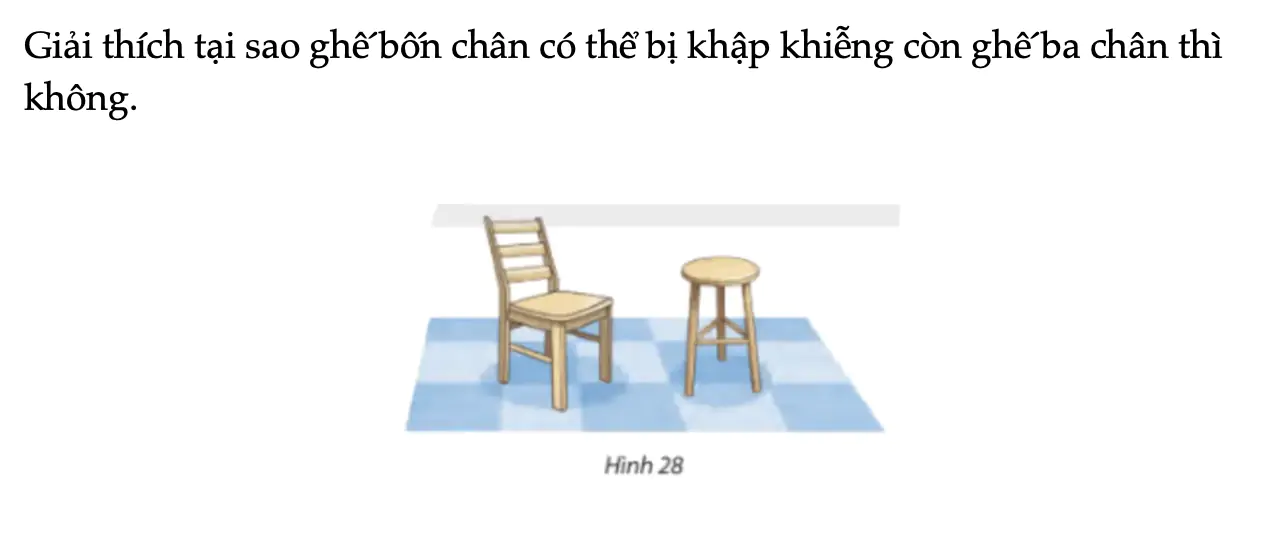
Vận dụng 2 trang 95 Toán 11 Tập 1
Giải thích tại sao ghế bốn chân có thể bị khập khiễng còn ghế ba chân thì không.

Vận dụng 3 trang 95 Toán 11 Tập 1
Trong xây dựng, người ta thường dùng máy quét tia laser để kẻ các đường thẳng trên tường hoặc sàn nhà. Tìm giao tuyến của mặt phẳng tạo bởi các tia laser OA và OB của các mặt tường trong Hình 29.

Hoạt động khám phá 10 trang 96 Toán 11 Tập 1
a) Các công trình kiến trúc, đồ vật trong Hình 30 có mặt bên là hình gì? b) Tìm diểm giống nhau của các hình trong Hình 31.
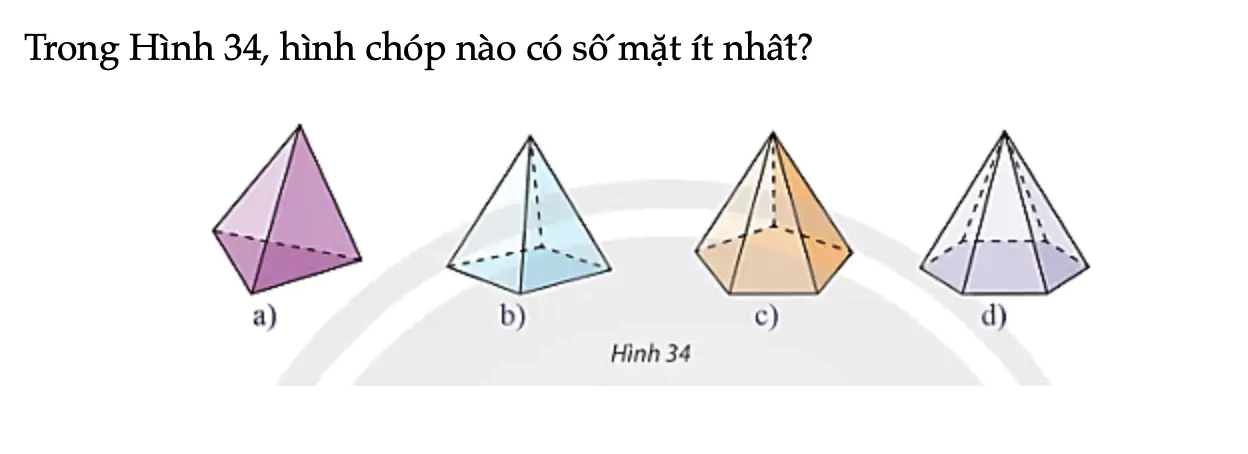
Hoạt động khám phá 11 trang 97 Toán 11 Tập 1
Trong Hình 34, hình chóp nào có số mặt ít nhất?
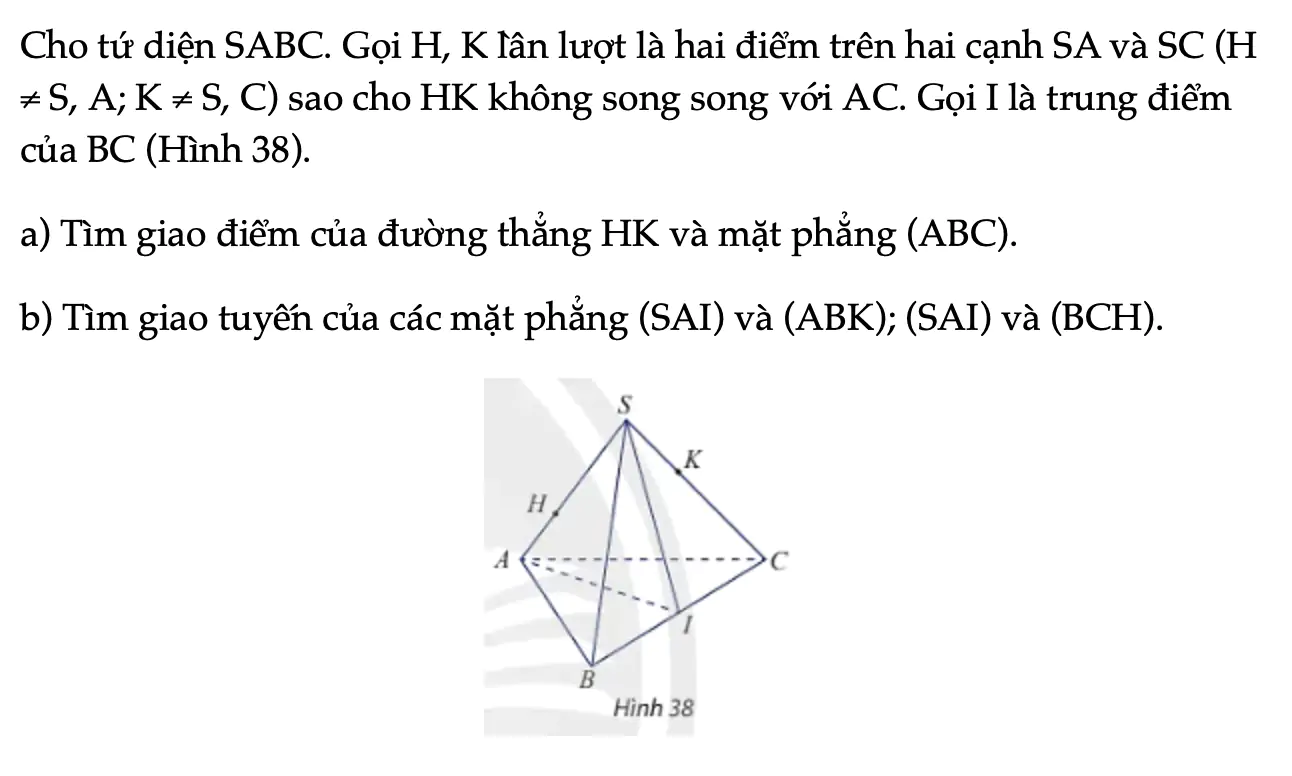
Thực hành 8 trang 98 Toán 11 Tập 1
Cho tứ diện SABC. Gọi H, K lần lượt là hai điểm trên hai cạnh SA và SC (H ≠ S, A; K ≠ S, C) sao cho HK không song song với AC. Gọi I là trung điểm của BC (Hình 38).
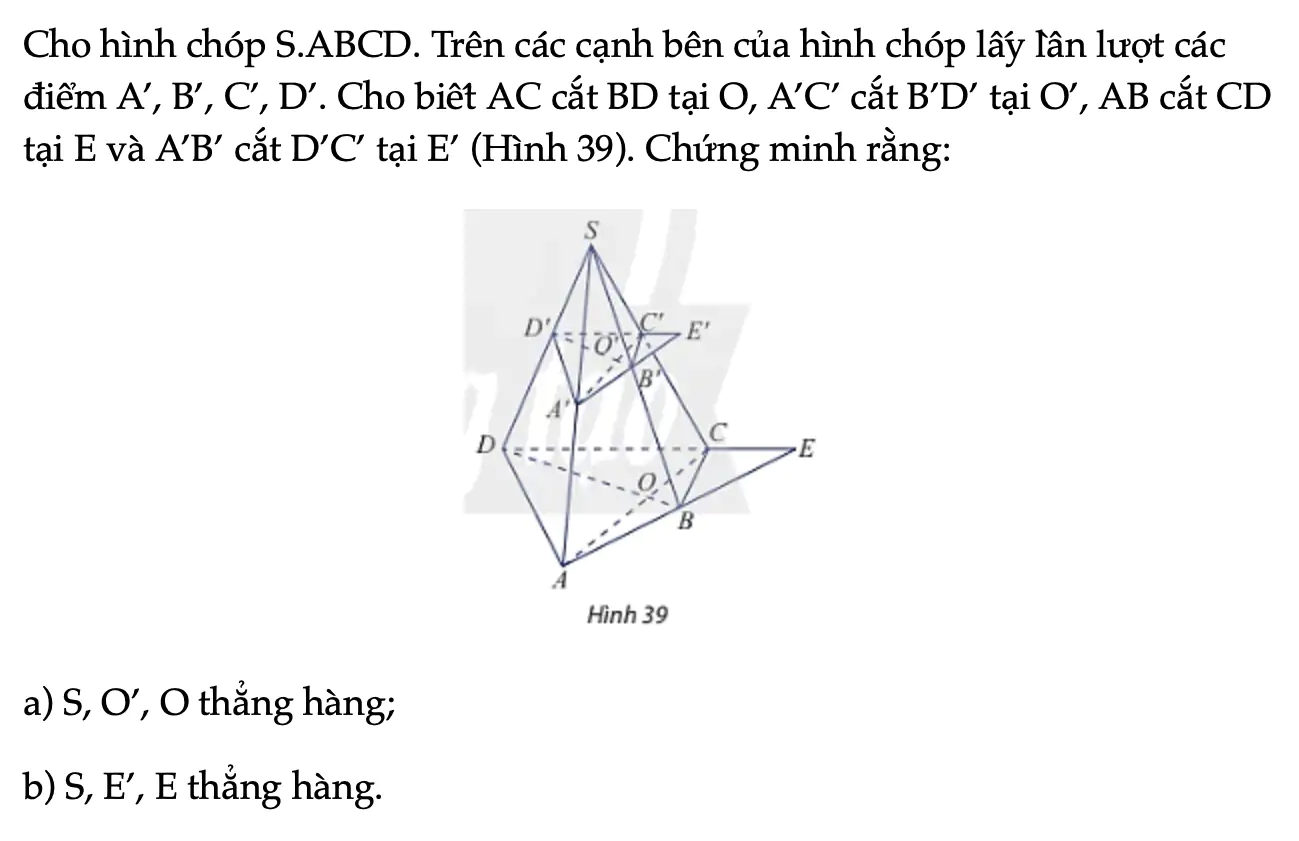
Vận dụng 4 trang 98 Toán 11 Tập 1
Cho hình chóp S.ABCD. Trên các cạnh bên của hình chóp lấy lần lượt các điểm A’, B’, C’, D’. Cho biết AC cắt BD tại O, A’C’ cắt B’D’ tại O’, AB cắt CD tại E và A’B’ cắt D’C’ tại E’ (Hình 39). Chứng minh rằng:
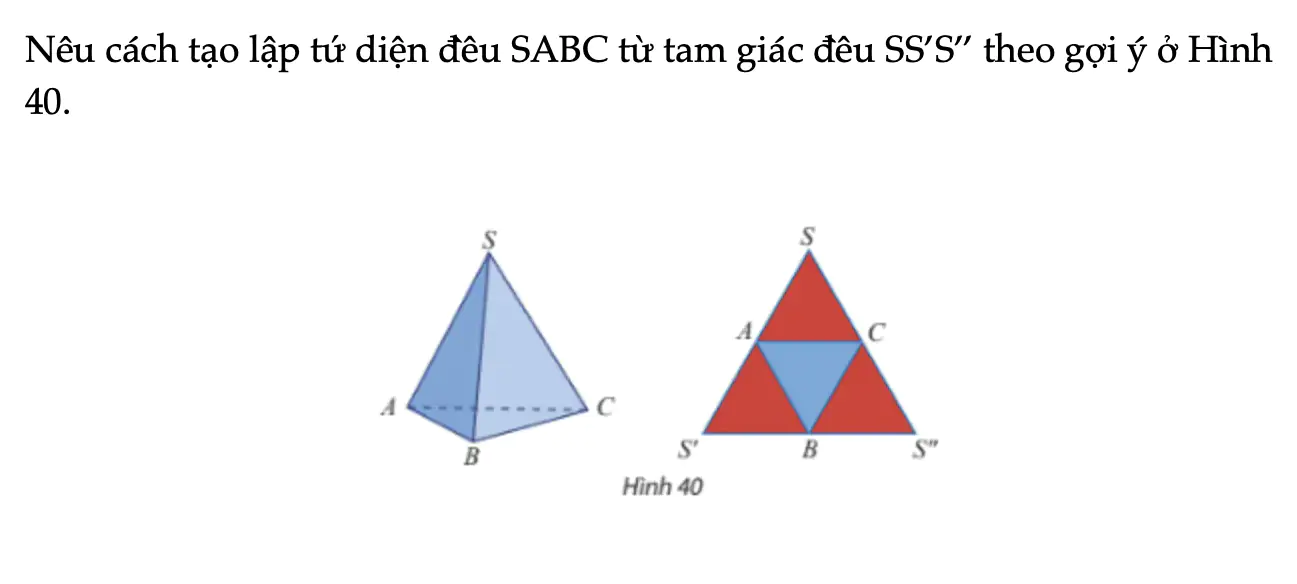
Vận dụng 5 trang 98 Toán 11 Tập 1
Nêu cách tạo lập tứ diện đều SABC từ tam giác đều SS’S’’ theo gợi ý ở Hình 40.
Giải bài tập Bài 2: Hai đường thẳng song song

Bài 1 trang 105 Toán 11 Tập 1
Cho hai đường thẳng song song a và b. Mệnh đề sau đây đúng hay sai. Bài 1 trang 105 Toán 11 Tập 1

Bài 2 trang 106 Toán 11 Tập 1
Hình chóp S.ABC và điểm M thuộc miền trong tam giác ABC (Hình 17). Qua M, vẽ đường thẳng d song song với SA, cắt (SBC). Trên hình vẽ, hãy chỉ rõ vị trí của điểm N và xác định giao tuyến của hai mặt phẳng (SAC) và (CMN). Bài 2 trang 106 Toán 11 Tập 1

Bài 3 trang 106 Toán 11 Tập 1
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Tìm giao tuyến của hai mặt phẳng (SCD) và (SAB). Bài 3 trang 106 Toán 11 Tập 1

Bài 4 trang 106 Toán 11 Tập 1
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi I là trung điểm của SD. Hai mặt phẳng (IAC) và (SBC) cắt nhau theo giao tuyến Cx. Chứng minh rằng Cx // SB. Bài 4 trang 106 Toán 11 Tập 1

Bài 5 trang 106 Toán 11 Tập 1
Cho hình chóp S.ABCD có đáy là hình bình hành, AC và BD cắt nhau tại O. Gọi I là trung điểm của SO. Mặt phẳng ICD cắt SA, SB lần lượt tại M, N. Bài 5 trang 106 Toán 11 Tập 1

Bài 6 trang 106 Toán 11 Tập 1
Chỉ ra các đường thẳng song song trong mỗi hình sau. Tìm thêm một ví dụ khác về các đường thẳng song song trong thực tế. Bài 6 trang 106 Toán 11 Tập 1

Hoạt động khởi động trang 100 Toán 11 Tập 1
Mô tả vị trí giữa các cặp đường thẳng a và b, b và c, c và d có trong hình bên
Hoạt động khám phá 1 trang 100 Toán 11 Tập 1
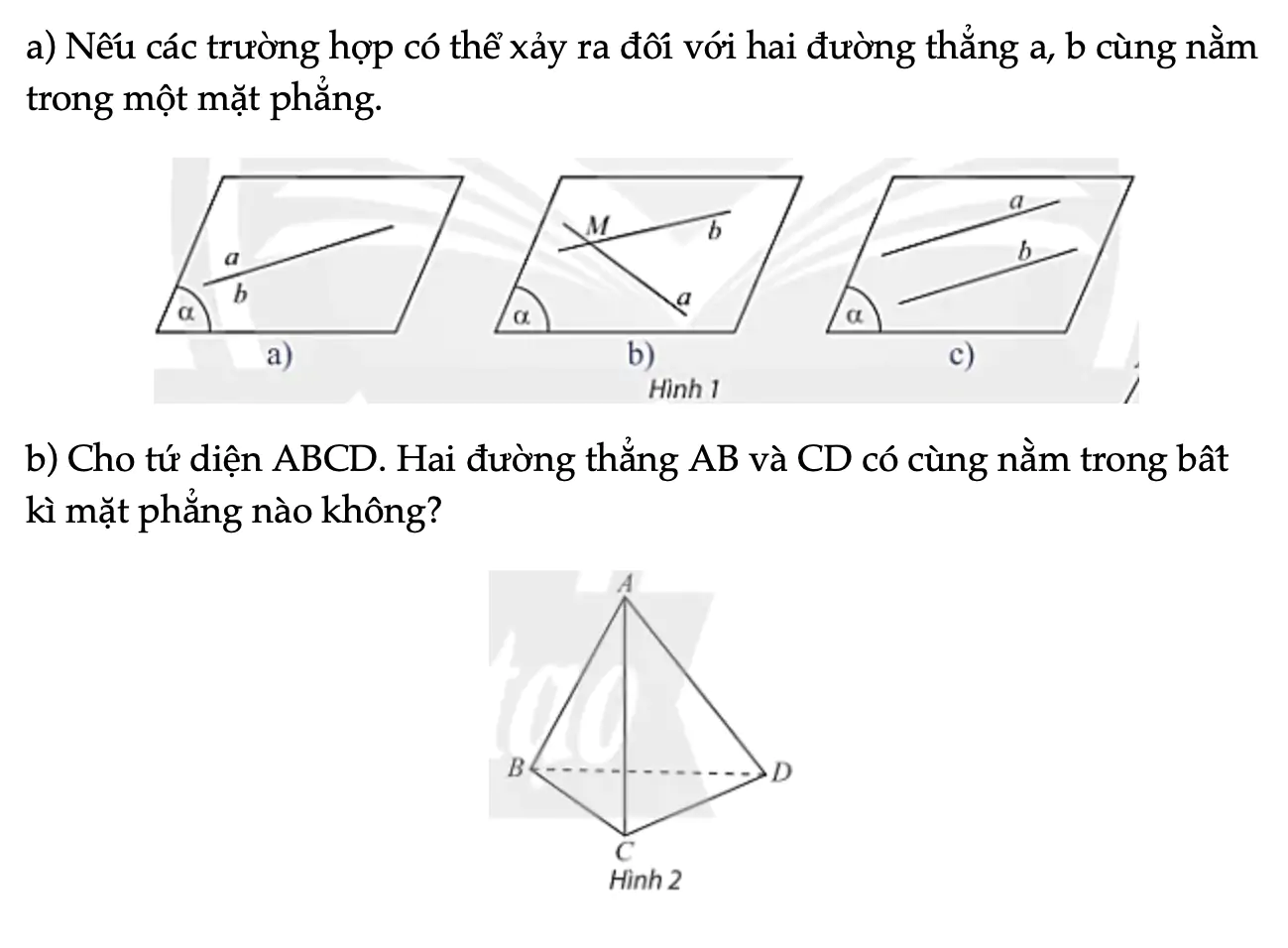
a) Nếu các trường hợp có thể xảy ra đối với hai đường thẳng a, b cùng nằm trong một mặt phẳng. b) Cho tứ diện ABCD. Hai đường thẳng AB và CD có cùng nằm trong bất kì mặt phẳng nào không?
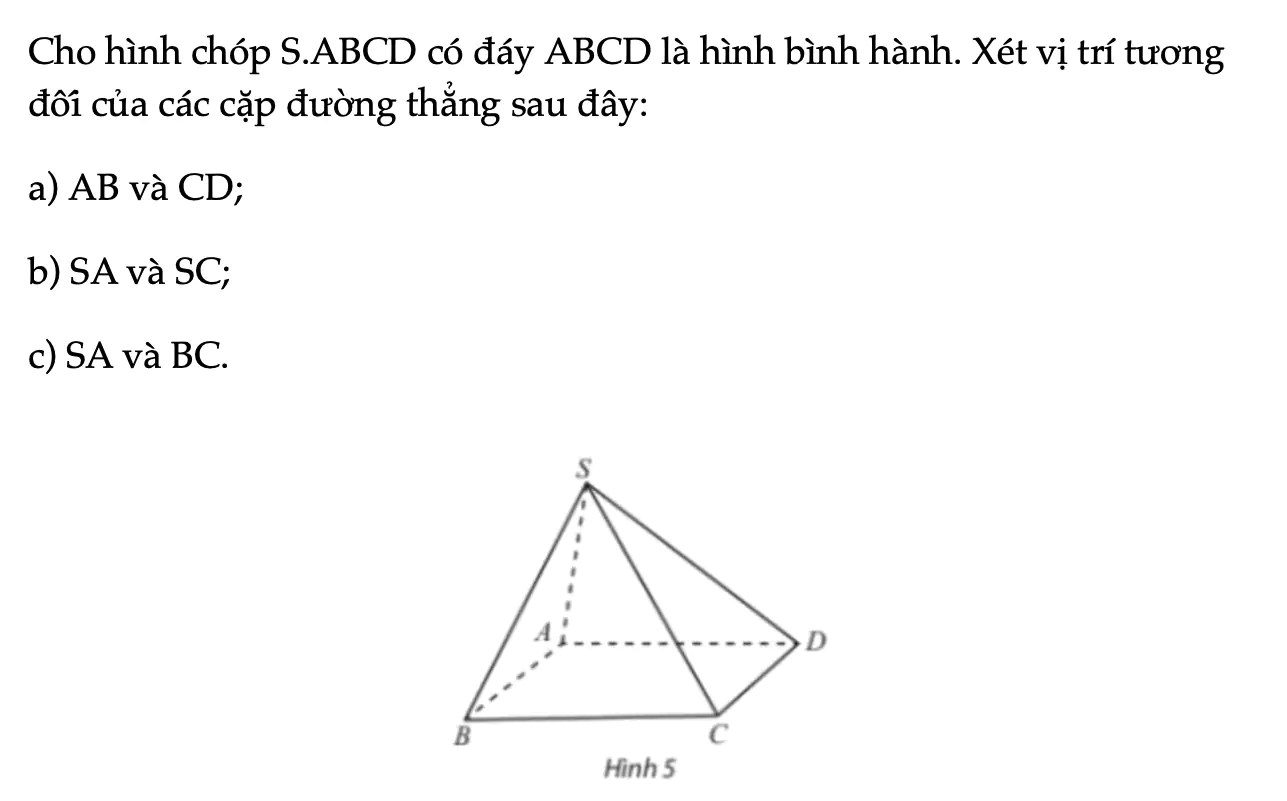
Thực hành 1 trang 101 Toán 11 Tập 1
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Xét vị trí tương đối của các cặp đường thẳng sau đây.

Vận dụng 1 trang 102 Toán 11 Tập 1
Hãy chỉ ra các ví dụ về hai đường thẳng song song, cắt nhau và chéo nhau trong hình cầu sắt ở Hình 6.
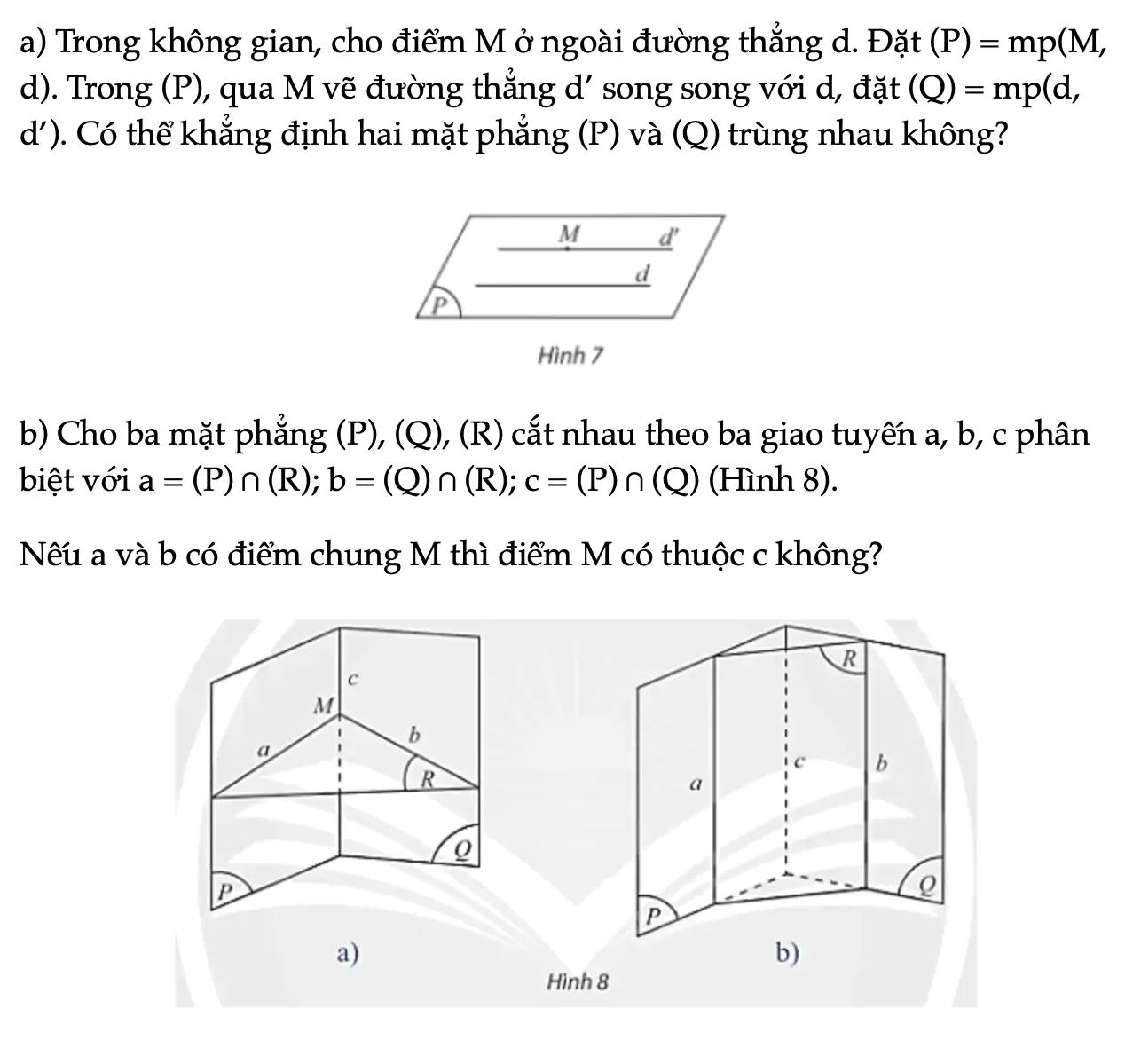
Hoạt động khám phá 2 trang 102 Toán 11 Tập 1
a) Trong không gian, cho điểm M ở ngoài đường thẳng d. Đặt (P) = mp(M, d). Trong (P), qua M vẽ đường thẳng d’ song song với d, đặt (Q) = mp(d, d’). Có thể khẳng định hai mặt phẳng (P) và (Q) trùng nhau không?

Thực hành 2 trang 103 Toán 11 Tập 1
Cho hình chóp S.ABCD. Vẽ hình thang ADMS có hai đáy là AD và MS. Gọi d là đường thẳng trong không gian đi qua S và song song với AD. Chứng minh đường thẳng d nằm trong mặt phẳng (SAD).
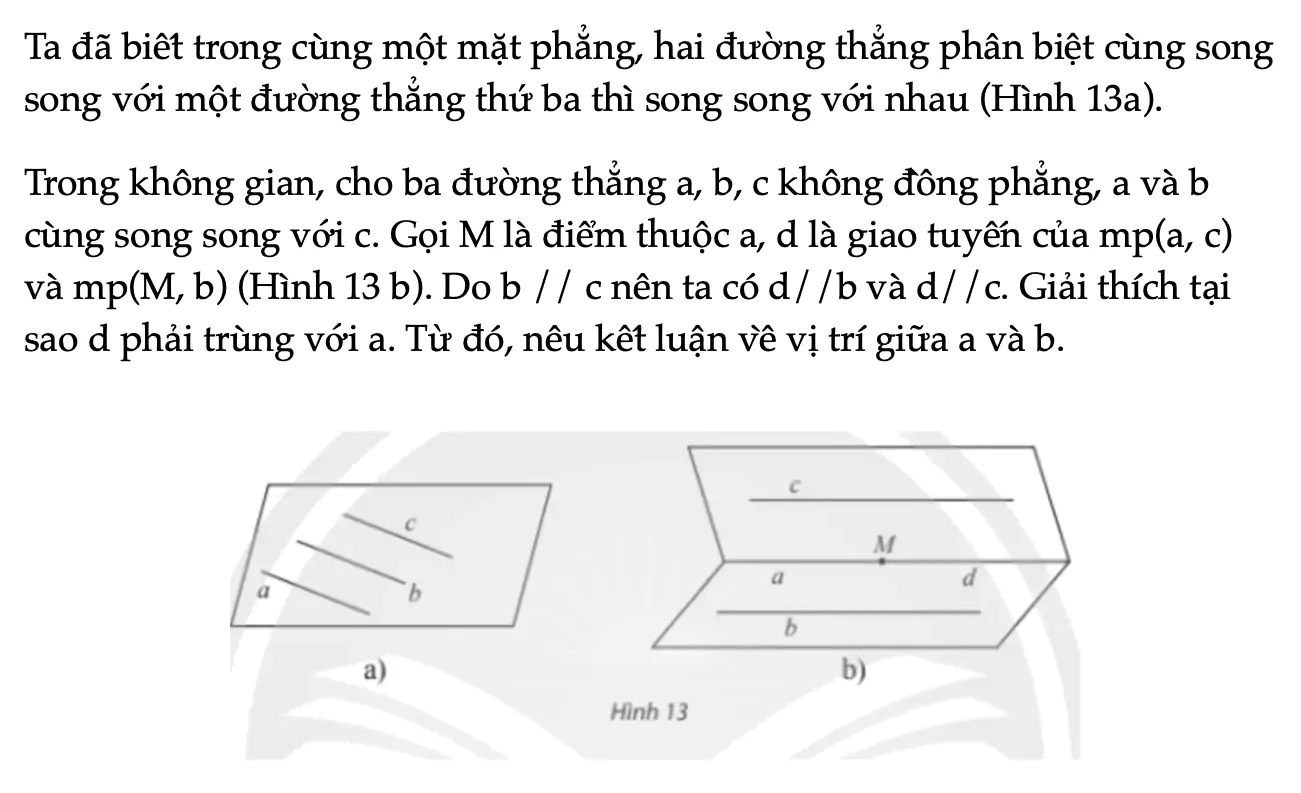
Hoạt động khám phá 3 trang 104 Toán 11 Tập 1
Ta đã biết trong cùng một mặt phẳng, hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba thì song song với nhau. Do b // c nên ta có d//b và d//c. Giải thích tại sao d phải trùng với a. Từ đó, nêu kết luận về vị trí giữa a và b.

Thực hành 3 trang 105 Toán 11 Tập 1
Cho tứ diện ABCD có I và J lần lượt là trung điểm của các cạnh BC và BD. Gọi (P) là mặt phẳng đi qua I, J và cắt hai cạnh AC và AD lần lượt tại M và N. a) Chứng minh IJNM là một hình thang. b) Tìm vị trí của điểm M để IJNM là hình bình hành.

Vận dụng 2 trang 105 Toán 11 Tập 1
Một chiếc lều (Hình 16a) được minh họa như Hình 16b. a) Tìm ba mặt phẳng cắt nhau từng đôi một theo ba giao tuyến song song. b) Tìm ba mặt phẳng cắt nhau từng đôi một theo ba giao tuyến đồng quy.
Giải bài tập Bài 3: Đường thẳng và mặt phẳng song song

Bài 1 trang 111 Toán 11 Tập 1
Cho hình chóp S.ABCD, đáy ABCD là hình bình hành có O là giao điểm hai đường chéo. Gọi M là trung điểm của SC. Bài 1 trang 111 Toán 11 Tập 1

Bài 2 trang 112 Toán 11 Tập 1
Cho hai hình bình hành ABCD và ABEF không nằm trong cùn một mặt phẳng. Gọi O và O’ lần lượt là tâm của ABCD và ABEF. Bài 2 trang 112 Toán 11 Tập 1

Bài 3 trang 112 Toán 11 Tập 1
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và một điểm M di động trên cạnh AD. Một mặt phẳng (α) qua M, song song với CD và SA, cắt BC, SC, SD lần lượt N, P, Q. Bài 3 trang 112 Toán 11 Tập 1
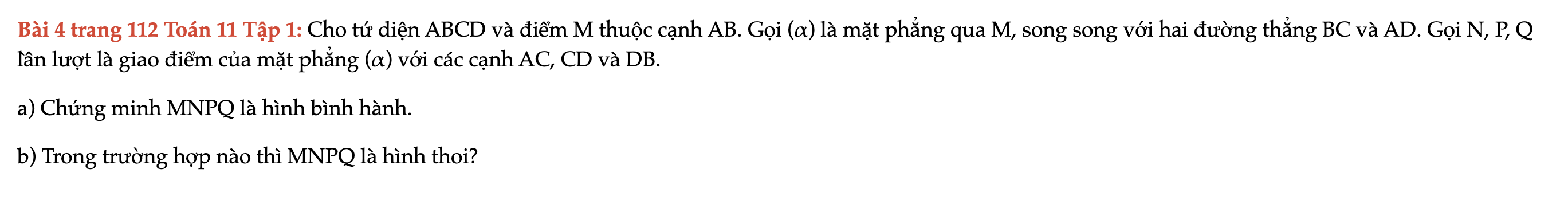
Bài 4 trang 112 Toán 11 Tập 1
Cho tứ diện ABCD và điểm M thuộc cạnh AB. Gọi (α) là mặt phẳng qua M, song song với hai đường thẳng BC và AD. Gọi N, P, Q lần lượt là giao điểm của mặt phẳng (α) với các cạnh AC, CD và DB. Bài 4 trang 112 Toán 11 Tập 1
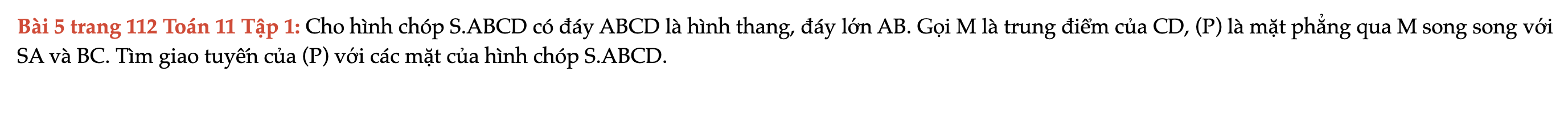
Bài 5 trang 112 Toán 11 Tập 1
Cho hình chóp S.ABCD có đáy ABCD là hình thang, đáy lớn AB. Gọi M là trung điểm của CD, (P) là mặt phẳng qua M song song với SA và BC. Tìm giao tuyến của (P) với các mặt của hình chóp S.ABCD. Bài 5 trang 112 Toán 11 Tập 1

Bài 6 trang 112 Toán 11 Tập 1
Mô tả vị trí tương đối của các đường thẳng a, b, c, d, e với mặt phẳng (P) là mặt trước của tòa nhà (Hình 19). Bài 6 trang 112 Toán 11 Tập 1

Hoạt động khởi động trang 107 Toán 11 Tập 1
Đường thẳng a trên mép hiên của tòa nhà có điểm nào chung với mặt (P) của phố đi bộ Nguyễn Huệ không?
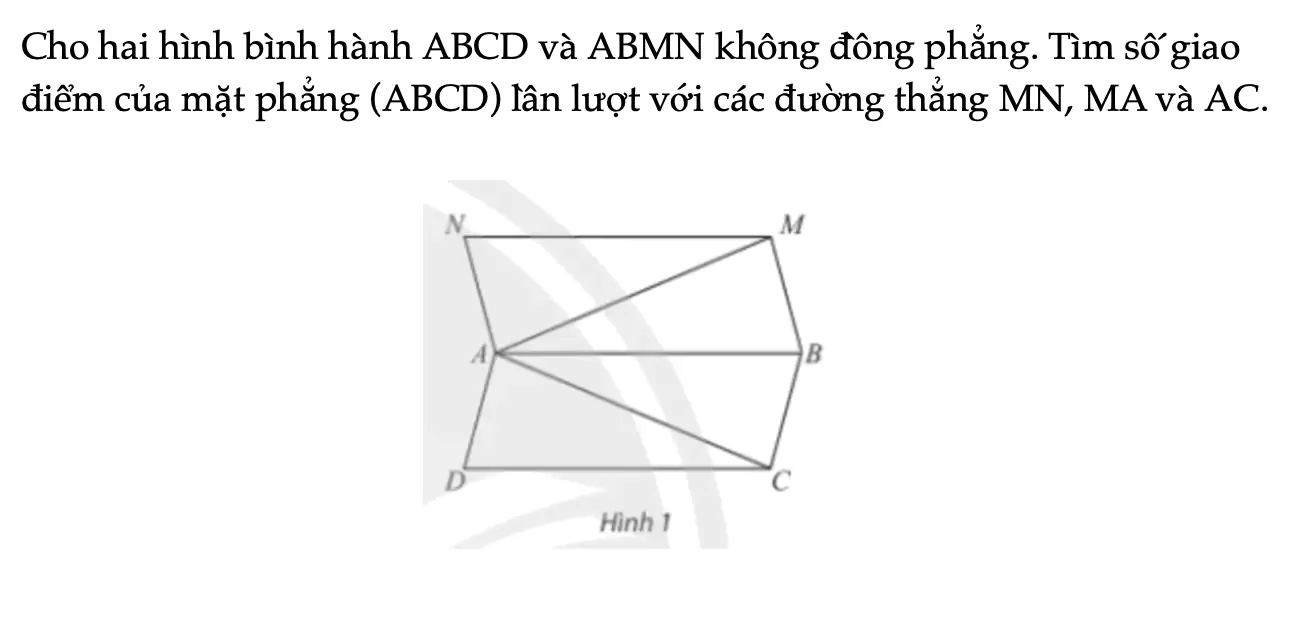
Hoạt động khám phá 1 trang 107 Toán 11 Tập 1
Cho hai hình bình hành ABCD và ABMN không đồng phẳng. Tìm số giao điểm của mặt phẳng (ABCD) lần lượt với các đường thẳng MN, MA và AC.
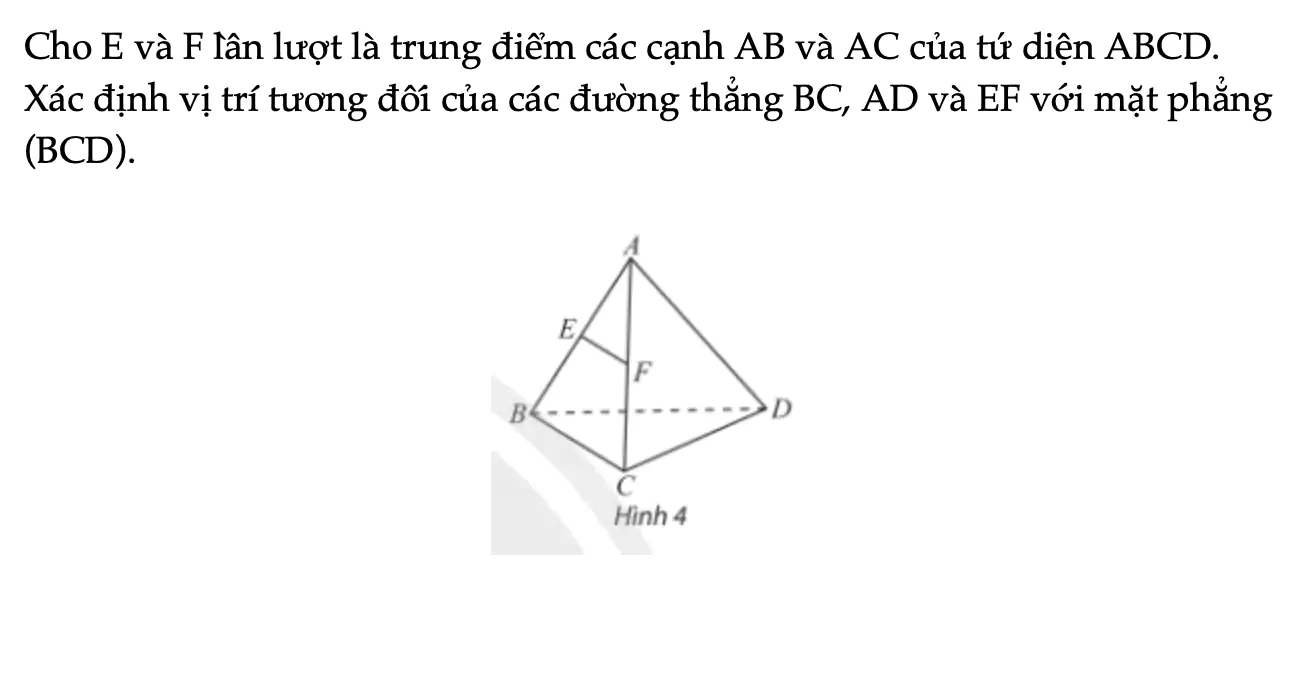
Thực hành 1 trang 108 Toán 11 Tập 1
Cho E và F lần lượt là trung điểm các cạnh AB và AC của tứ diện ABCD. Xác định vị trí tương đối của các đường thẳng BC, AD và EF với mặt phẳng (BCD).

Hoạt động khám phá 2 trang 108 Toán 11 Tập 1
Cho đường thẳng a không nằm trong mặt phẳng (P) và song song với một đường thẳng b nằm trong (P). Đặt (Q) = mp(a, b). a) Tìm giao tuyến của hai mặt phẳng (P) và (Q). b) Giả sử a có điểm chung M với (P) thì điểm M phải nằm trên đường thẳng nào?
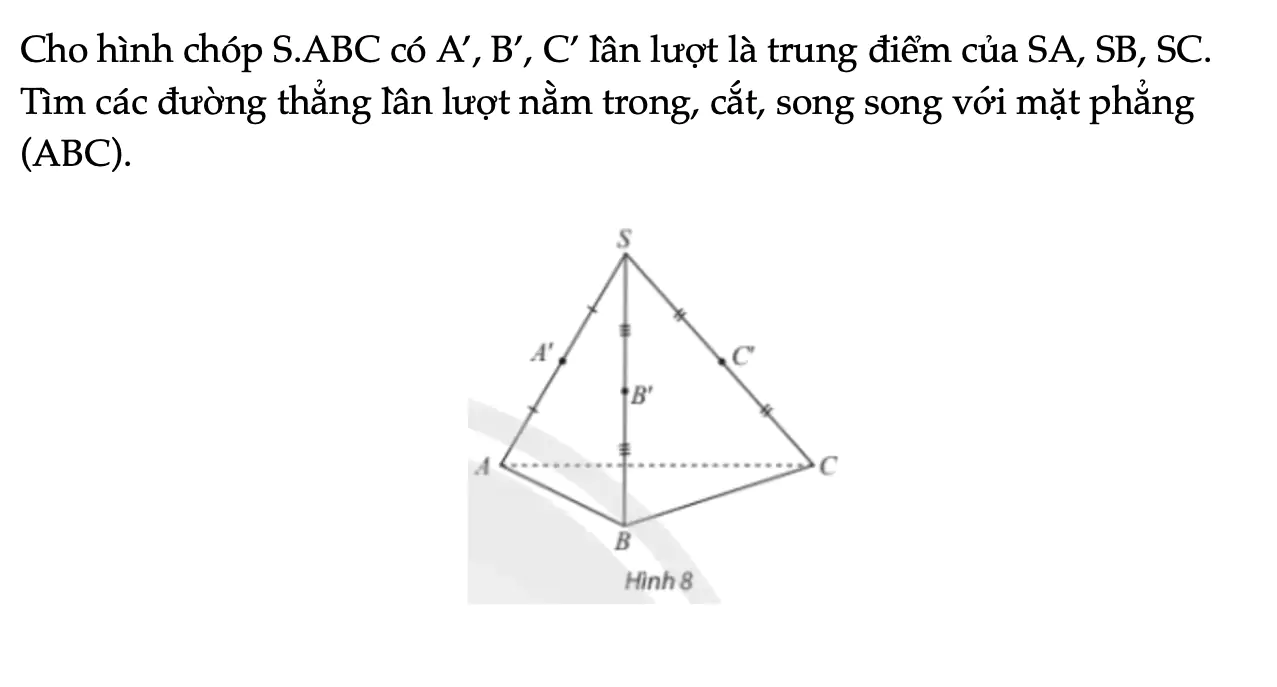
Thực hành 2 trang 109 Toán 11 Tập 1
Cho hình chóp S.ABC có A’, B’, C’ lần lượt là trung điểm của SA, SB, SC. Tìm các đường thẳng lần lượt nằm trong, cắt, song song với mặt phẳng (ABC).

Vận dụng 1 trang 109 Toán 11 Tập 1
Hãy chỉ ra trong Hình 9 các đường thẳng lần lượt nằm trong, song song, cắt mặt phẳng sàn nhà.
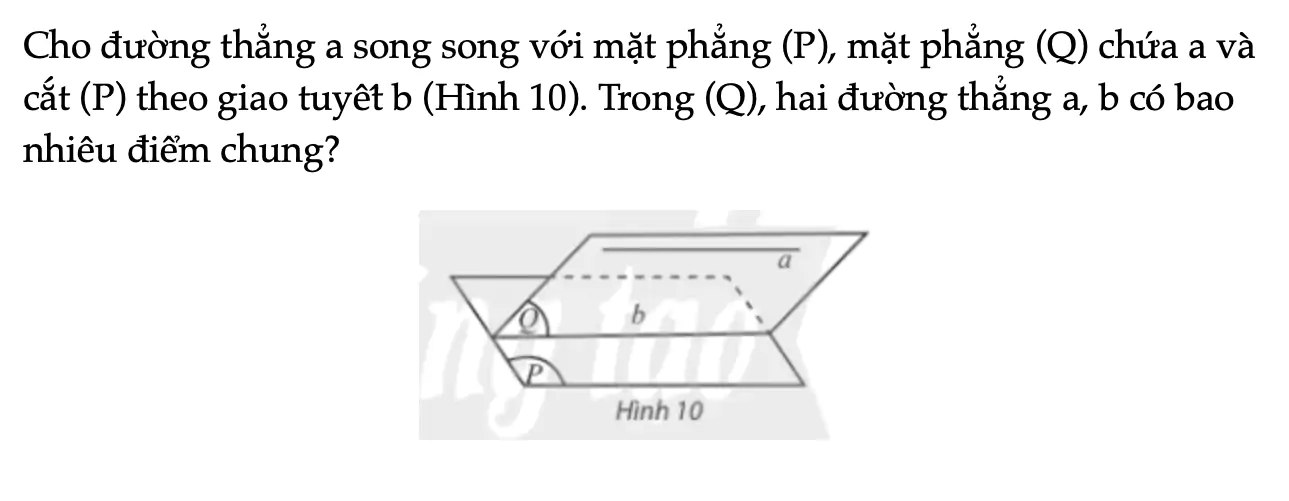
Hoạt động khám phá 3 trang 109 Toán 11 Tập 1
Cho đường thẳng a song song với mặt phẳng (P), mặt phẳng (Q) chứa a và cắt (P) theo giao tuyết b (Hình 10). Trong (Q), hai đường thẳng a, b có bao nhiêu điểm chung?

Hoạt động khám phá 4 trang 110 Toán 11 Tập 1
Cho hai đường thẳng chéo nhau a, b. Lấy một điểm M trên a, vẽ đường thẳng b’ đi qua M và song song với b. Đặt (P) là mặt phẳng đi qua a, b’.
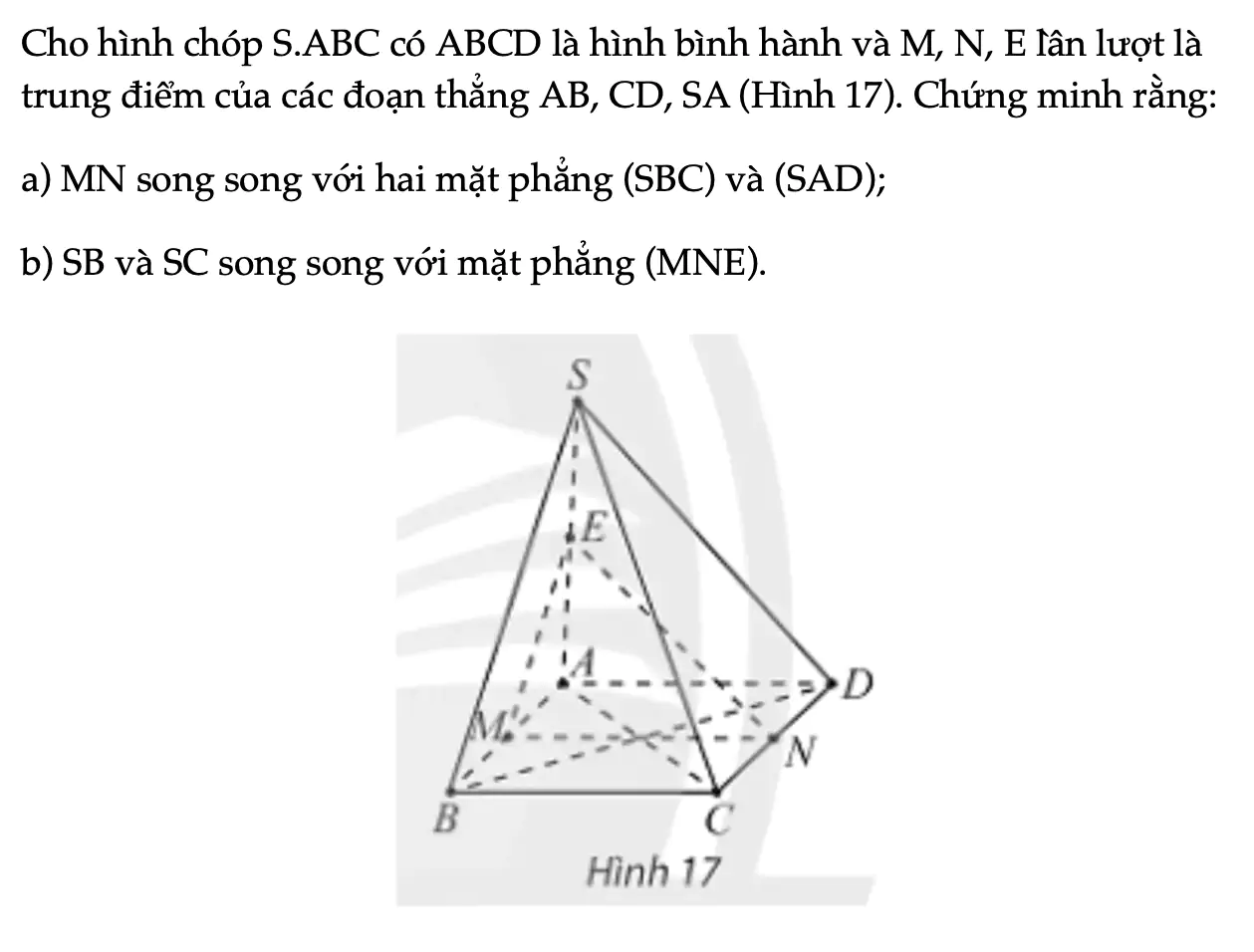
Thực hành 3 trang 111 Toán 11 Tập 1
Cho hình chóp S.ABC có ABCD là hình bình hành và M, N, E lần lượt là trung điểm của các đoạn thẳng AB, CD, SA (Hình 17). Chứng minh rằng: a) MN song song với hai mặt phẳng (SBC) và (SAD); b) SB và SC song song với mặt phẳng (MNE).

Vận dụng 2 trang 111 Toán 11 Tập 1
Làm thế nào để đặt cây thước kẻ a để nó song song với các trang của một cuốn sách?
Giải bài tập Bài 4: Hai mặt phẳng song song

Bài 1 trang 119 Toán 11 Tập 1
Trong mặt phẳng (P) cho hình bình hành ABCD. Ta dựng các nửa đường thẳng song song với nhau và nằm về một phía đối với (P) lần lượt đi qua các điểm A, B, C, D. Bài 1 trang 119 Toán 11 Tập 1

Bài 2 trang 120 Toán 11 Tập 1
Cho hình chóp S.ABCD, đáy ABCD là hình bình hành có O là giao điểm của hai đường chéo. Gọi M, N lần lượt là trung điểm của SA, SD. Bài 2 trang 120 Toán 11 Tập 1

Bài 3 trang 120 Toán 11 Tập 1
Cho hai hình vuông ABCD và ABEF ở trong hai mặt phẳng khác nhau. Trên các đường chéo AC và BF lần lượt lấy các điểm M, N sao cho AM = BN. Các đường thẳng song song với AB vẽ từ M, N lần lượt cắt AD, AF tại M’, N’. Bài 3 trang 120 Toán 11 Tập 1

Bài 4 trang 120 Toán 11 Tập 1
Cho hình hộp ABCD.A’B’C’D’. Gọi G1 và G2 lần lượt là trọng tâm của hai tam giác BDA’ và B’D’C. Chứng minh G1 và G2 chia đoạn AC’ thành ba phần bằng nhau. Bài 4 trang 120 Toán 11 Tập 1

Bài 5 trang 120 Toán 11 Tập 1
Để làm một khung lồng đèn kéo quân hình lăng trụ lục giác ABCDEF.A’B’C’D’E’F’, Bình gắn hai thanh tre A1D1, F1C1 song song với mặt phẳng đáy và cắt nhau tại O1 (Hình 19). Bài 5 trang 120 Toán 11 Tập 1

Bài 6 trang 120 Toán 11 Tập 1
Chỉ ra các mặt phẳng song song trong mỗi hình sau. Tìm thêm một số ví dụ khác về mặt phẳng song song trong thực tế. Bài 6 trang 120 Toán 11 Tập 1

Hoạt động khởi động trang 113 Toán 11 Tập 1
Bề mặt trên của mỗi bậc thang này được đặt như thế nào so với mặt đất?

Hoạt động khám phá 1 trang 113 Toán 11 Tập 1
Hộp giấy có các mặt là hình vuông ở Hình 1a được vé lại với các đỉnh là A, B, C, D, A’, B’, C’, D’ như Hình 1b. Gọi tên cặp mặt phẳng: a) Có ba điểm chung không thẳng hàng. b) Là hai mặt phẳng phân biệt và có một điểm chung. c) Không có điểm chung nào.

Vận dụng 1 trang 114 Toán 11 Tập 1
Tìm một số mặt phẳng song song có trong hình chụp căn phòng ở Hình 4.

Hoạt động khám phá 2 trang 114 Toán 11 Tập 1
Cho mặt phẳng (P) chứa hai đường thẳng a, b cắt nhau và cùng song song với mặt phẳng (Q). Giả sử (P) và (Q) có điểm chung M thì (P) cắt (Q) theo giao tuyến c (Hình 5).

Thực hành 1 trang 115 Toán 11 Tập 1
Cho tứ diện ABCD có E, F, H lần lượt là trung điểm của AB, AC, AD. Chứng minh (EFH) // (BCD).

Hoạt động khám phá 3 trang 115 Toán 11 Tập 1
a) Cho điểm A ở ngoài mặt phẳng (Q). Trong (Q) vẽ hai đường thẳng cắt nhau a’ và b’. Làm thế nào để vẽ hai đường thẳng a và b đi qua A và song song với (Q)? b) Có nhận xét gì về mối liên hệ giữa mp(a, b) và (Q)?
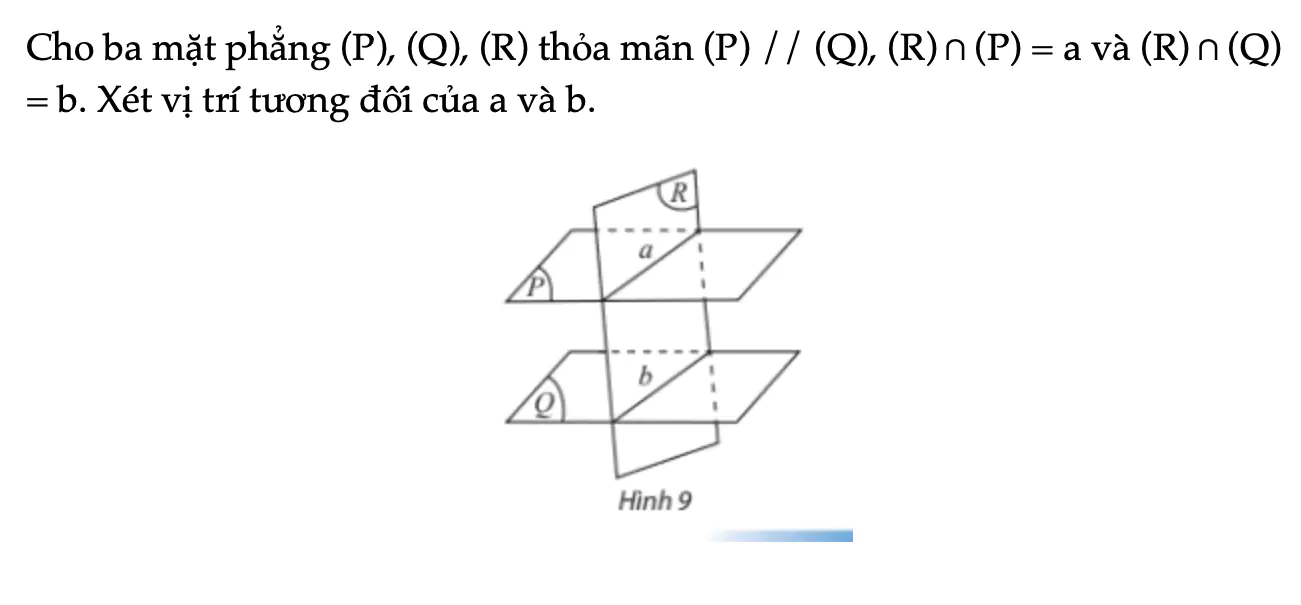
Hoạt động khám phá 4 trang 115 Toán 11 Tập 1
Cho ba mặt phẳng (P), (Q), (R) thỏa mãn (P) // (Q), (R) ∩ (P) = a và (R) ∩ (Q) = b. Xét vị trí tương đối của a và b.

Thực hành 2 trang 116 Toán 11 Tập 1
Cho hình chóp S.ABCD với đáy ABCD là hình bình hành có O là giao điểm của hai đường chéo, tam giác SBD là tam giác đều. Một mặt phẳng (α) di động song song với mặt phẳng (SBD) và cắt đoạn thằng AC. Chứng minh rằng:

Vận dụng 2 trang 116 Toán 11 Tập 1
Khi dùng dao cắt các lớp bánh (Hình 11), giả sử bề mặt các lớp bánh là các mặt phẳng song song và con dao được xem như mặt phẳng (P), nêu kết luận về các giao tuyến tạo bởi (P) với các bề mặt của các lớp bánh. Giải thích.
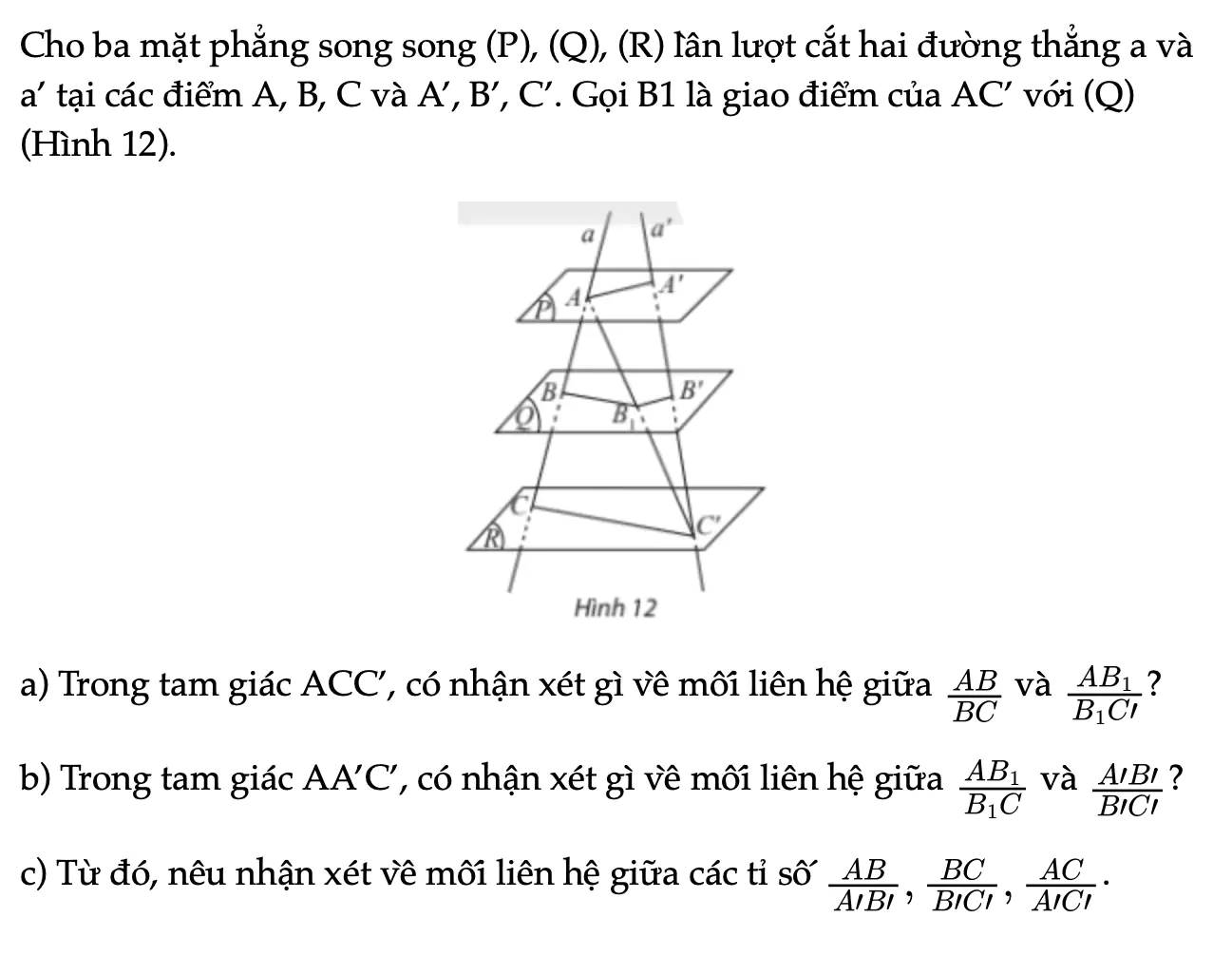
Hoạt động khám phá 5 trang 116 Toán 11 Tập 1
Cho ba mặt phẳng song song (P), (Q), (R) lần lượt cắt hai đường thẳng a và a’ tại các điểm A, B, C và A’, B’, C’. Gọi B1 là giao điểm của AC’ với (Q) (Hình 12).

Thực hành 3 trang 117 Toán 11 Tập 1
Cho hình chóp S.ABC có SA = 9, SB = 12, SC = 15. Trên cạnh SA lấy điểm M, N sao cho SM = 4, MN = 3, NA = 2. Vẽ hai mặt phẳng song song với mặt phẳng (ABC), lần lượt đi qua M, N, cắt SB theo thứ tự tại M’, N’ và cắt SC theo thứ tự tại M”, N”.

Hoạt động khám phá 6 trang 117 Toán 11 Tập 1
Hình dạng của các đồ vật như hộp phấn, lồng đèn, hộp quà, lăng kính có đặc điểm gì giống nhau?
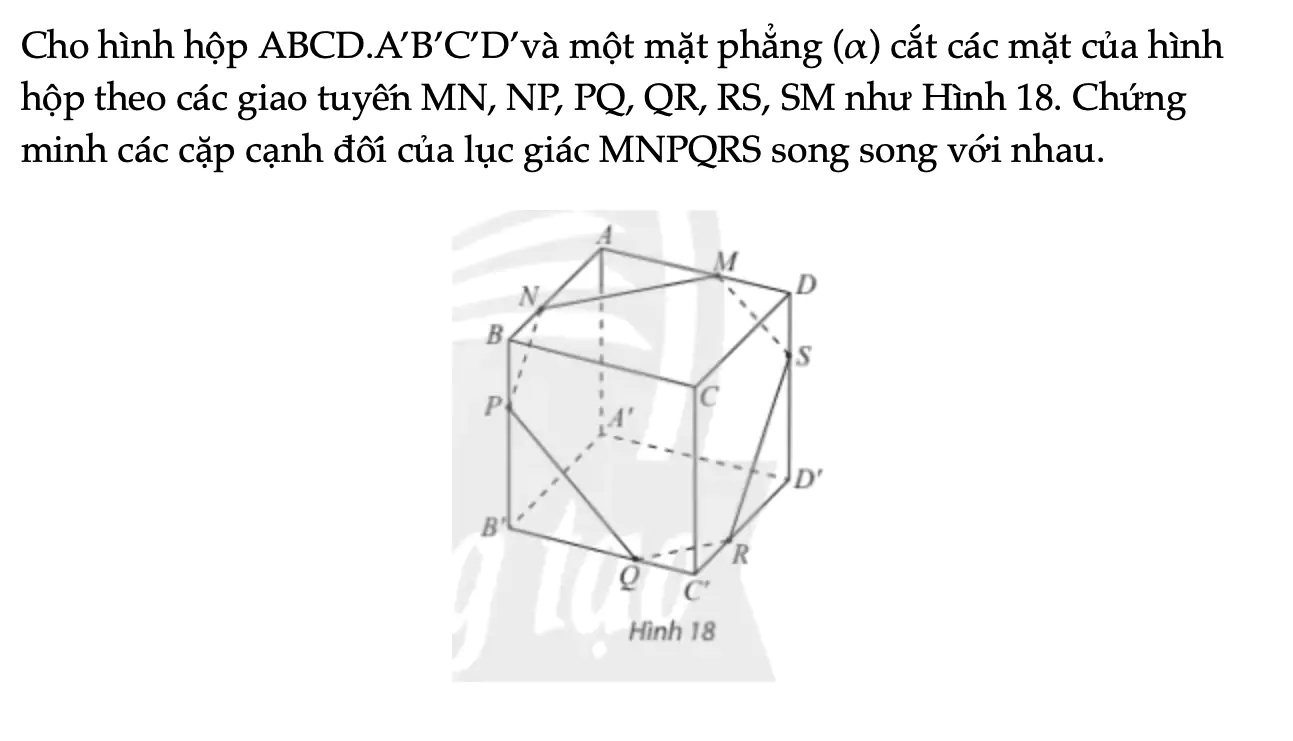
Thực hành 4 trang 119 Toán 11 Tập 1
Cho hình hộp ABCD.A’B’C’D’và một mặt phẳng (α) cắt các mặt của hình hộp theo các giao tuyến MN, NP, PQ, QR, RS, SM như Hình 18. Chứng minh các cặp cạnh đối của lục giác MNPQRS song song với nhau.
Vận dụng 3 trang 119 Toán 11 Tập 1
Tìm hình lăng trụ có thể lấy một mặt bất kì làm mặt đáy.
Giải bài tập Bài 5: Phép chiếu song song

Bài 1 trang 126 Toán 11 Tập 1
Trong các mệnh đề sau, mệnh đề nào đúng. Bài 1 trang 126 Toán 11 Tập 1

Bài 2 trang 126 Toán 11 Tập 1
Vẽ hình biểu diễn của một lục giác đều. Bài 2 trang 126 Toán 11 Tập 1

Bài 3 trang 126 Toán 11 Tập 1
Vẽ hình biểu diễn của một hình vuông nội tiếp trong một hình tròn. Bài 3 trang 126 Toán 11 Tập 1

Bài 4 trang 126 Toán 11 Tập 1
Cho hai điểm A, B nằm ngoài mặt phẳng (α) và đường thẳng d cắt (α). Giả sử đường thẳng AB cắt (α) tại điểm O. Gọi A’ và B’ lần lượt là hình chiếu song song của A và B trên (α) theo phương của đường thẳng d. Bài 4 trang 126 Toán 11 Tập 1

Bài 5 trang 126 Toán 11 Tập 1
Vẽ hình biểu diễn của hình lăng trụ có đáy là tam giác đều. Bài 5 trang 126 Toán 11 Tập 1
Hoạt động khởi động trang 121 Toán 11 Tập 1
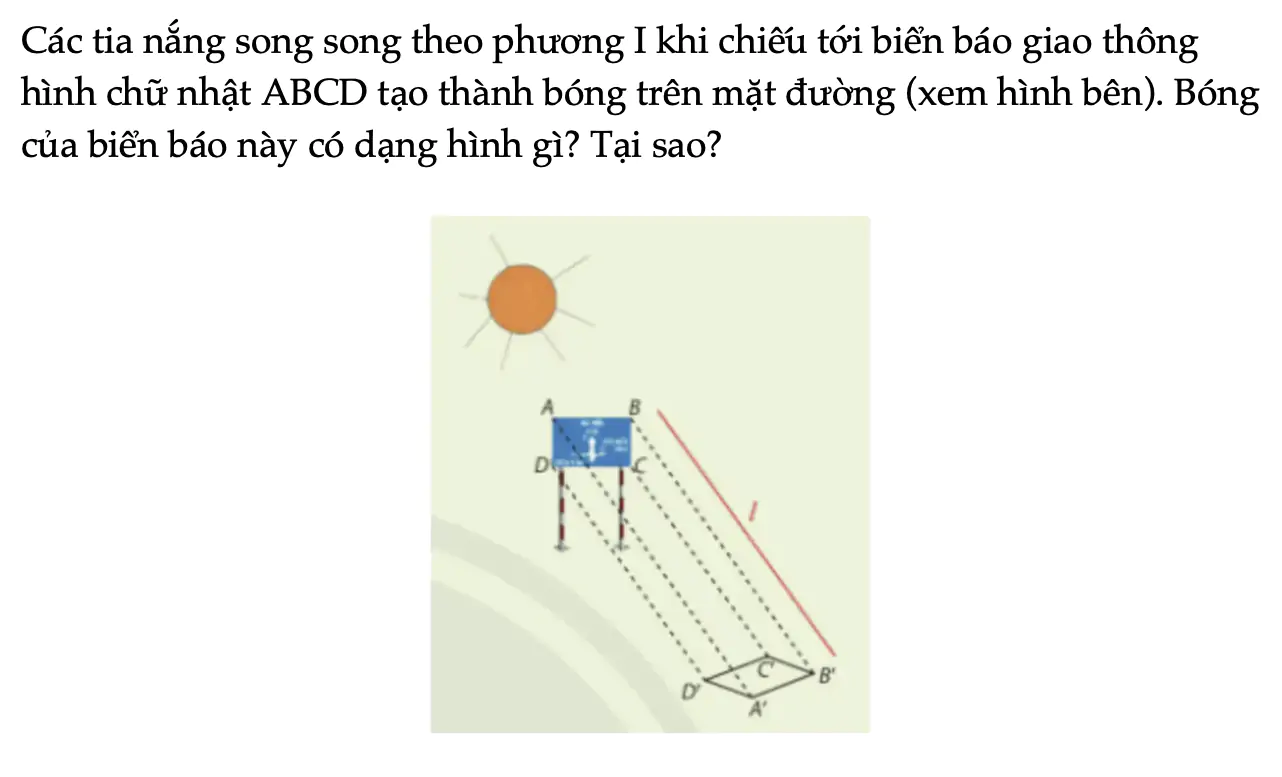
Các tia nắng song song theo phương I khi chiếu tới biển báo giao thông hình chữ nhật ABCD tạo thành bóng trên mặt đường (xem hình bên). Bóng của biển báo này có dạng hình gì? Tại sao?

Hoạt động khám phá 1 trang 121 Toán 11 Tập 1
Trong hoạt động khởi động: a) Các tia sáng AA’, BB’, DD’ có song song với nhau hay không? b) Nêu cách xác định bóng C’ của điểm C trên mặt đường.
Thực hành 1 trang 122 Toán 11 Tập 1
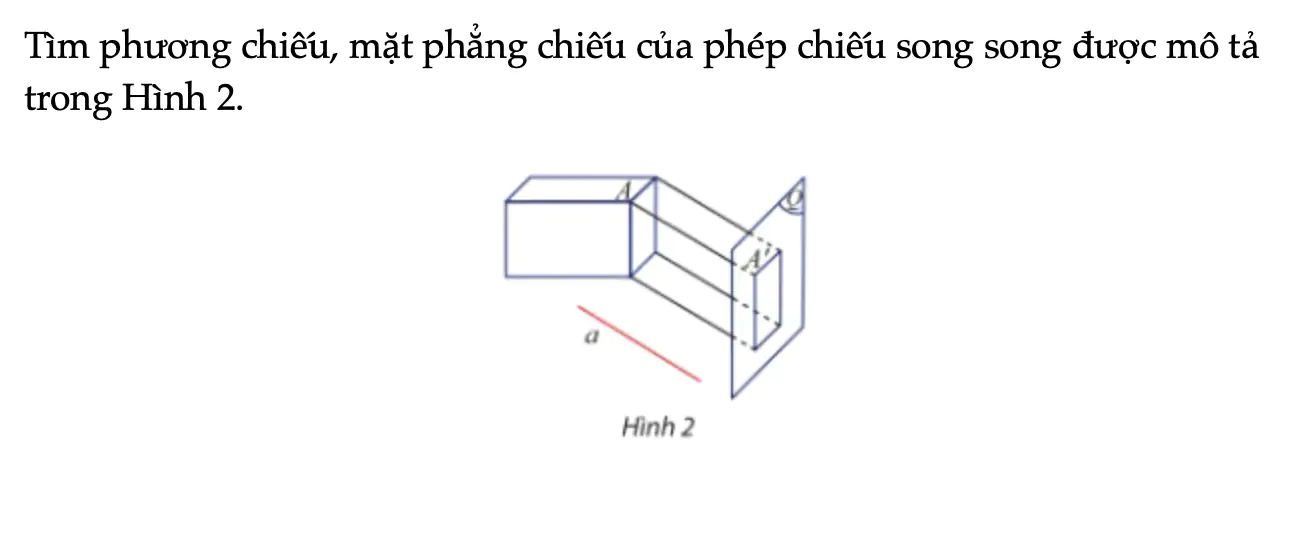
Tìm phương chiếu, mặt phẳng chiếu của phép chiếu song song được mô tả trong Hình 2.
Vận dụng 1 trang 122 Toán 11 Tập 1
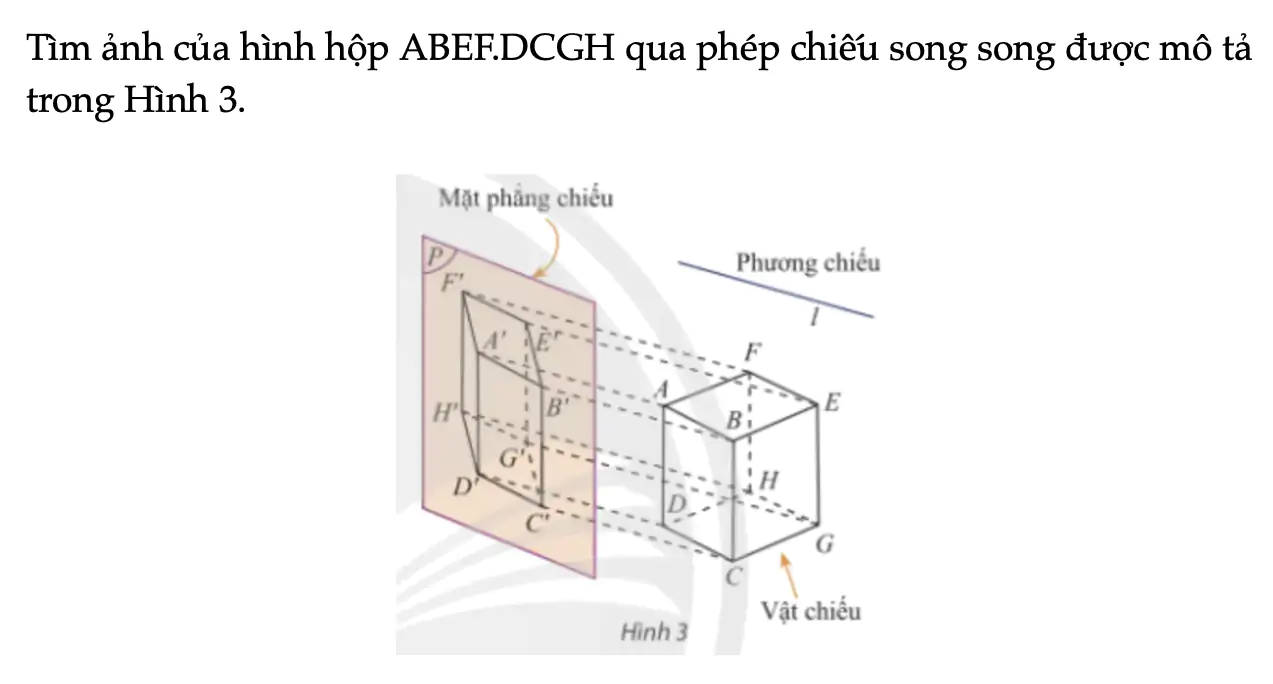
Tìm ảnh của hình hộp ABEF.DCGH qua phép chiếu song song được mô tả trong Hình 3.
Hoạt động khám phá 2 trang 122 Toán 11 Tập 1
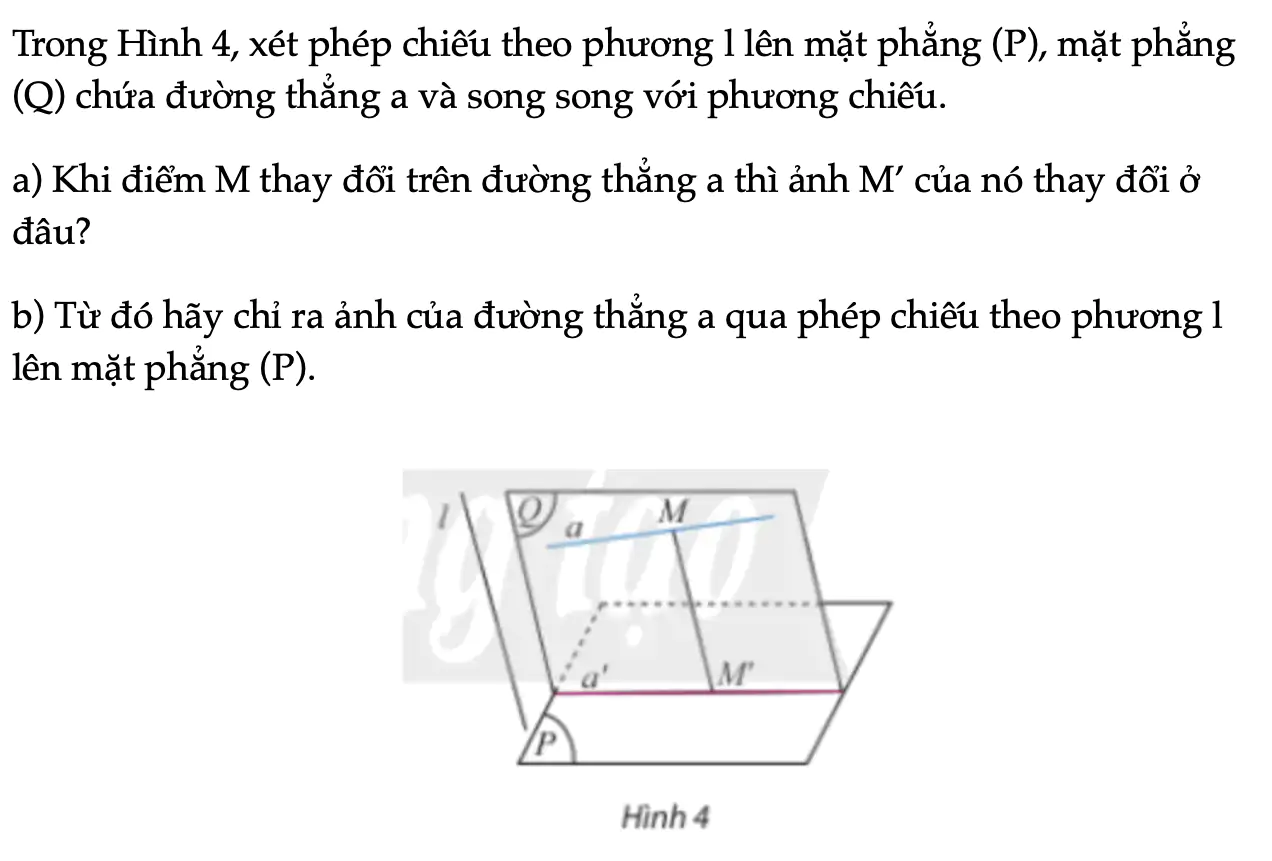
Trong Hình 4, xét phép chiếu theo phương l lên mặt phẳng (P), mặt phẳng (Q) chứa đường thẳng a và song song với phương chiếu.
Hoạt động khám phá 3 trang 123 Toán 11 Tập 1
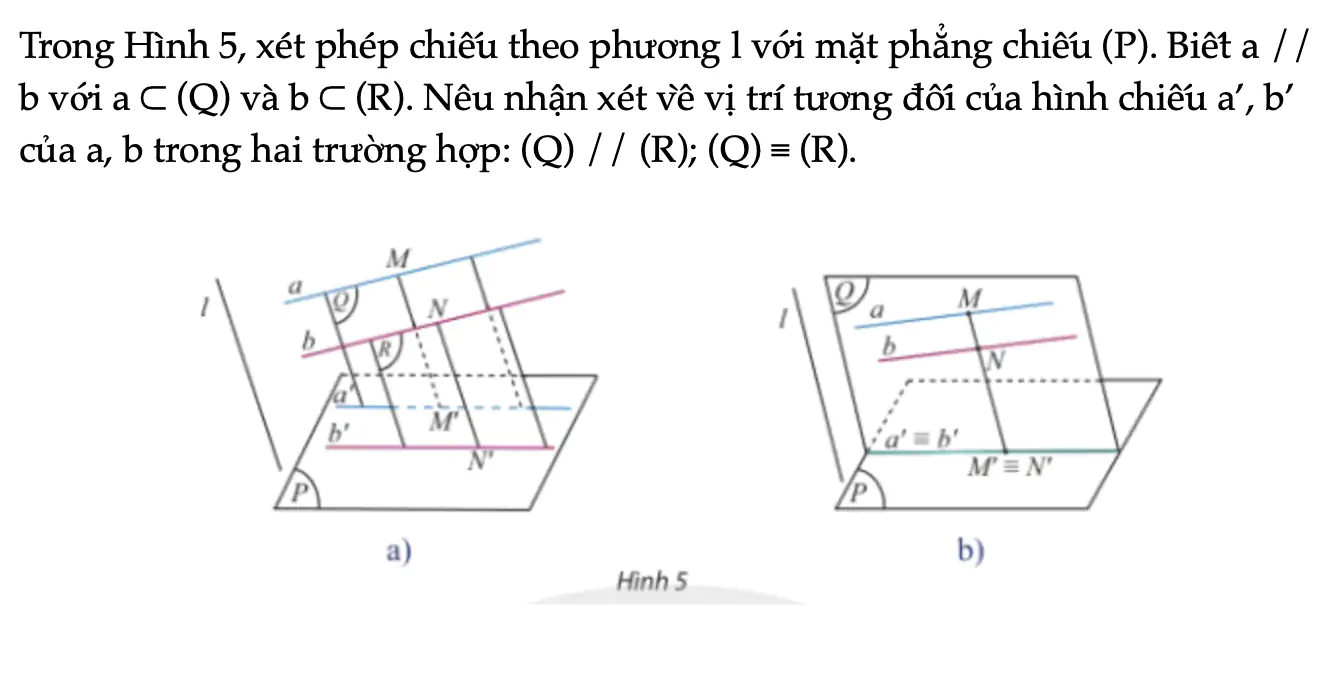
Trong Hình 5, xét phép chiếu theo phương l với mặt phẳng chiếu (P). Biết a // b với a ⊂ (Q) và b ⊂ (R). Nêu nhận xét về vị trí tương đối của hình chiếu a’, b’ của a, b trong hai trường hợp: (Q) // (R); (Q) ≡ (R).
Thực hành 2 trang 124 Toán 11 Tập 1
Cho hình thang ABCD có đáy lớn AB và AB = 2CD, hình chiếu song song của ABCD là tứ giác A’B’C’D’. Chứng minh rằng A’B’C’D’ cũng là một hình thang và A’B’ = 2C’D’.

Vận dụng 2 trang 124 Toán 11 Tập 1
Cho G là trọng tâm tam giác ABC, M là trung điểm BC và hình chiếu song song của tam giác ABC là tam giác A’B’C’. Chứng minh rằng hình chiếu M’ của M là trung điểm của B’C’ và hình chiếu G’ của G cũng là trọng tâm tam giác A’B’C’.
Hoạt động khám phá 4 trang 124 Toán 11 Tập 1
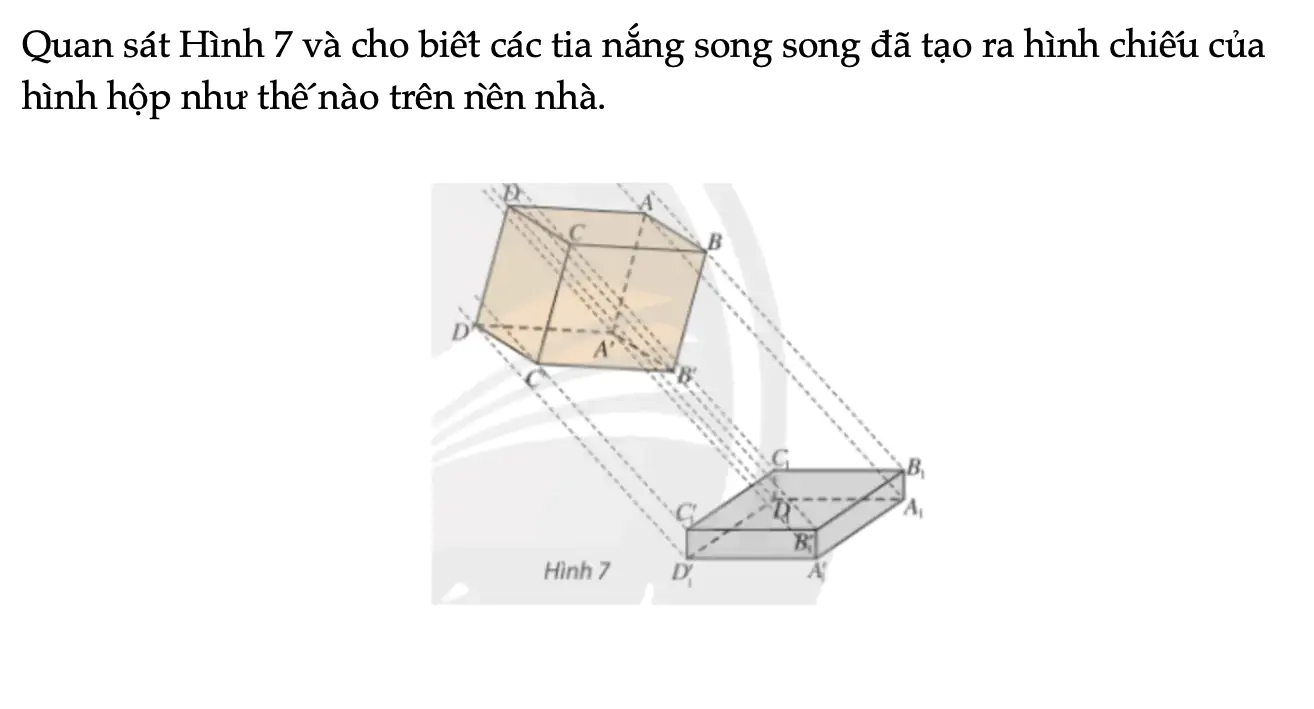
Quan sát Hình 7 và cho biết các tia nắng song song đã tạo ra hình chiếu của hình hộp như thế nào trên nền nhà.
Thực hành 3 trang 126 Toán 11 Tập 1
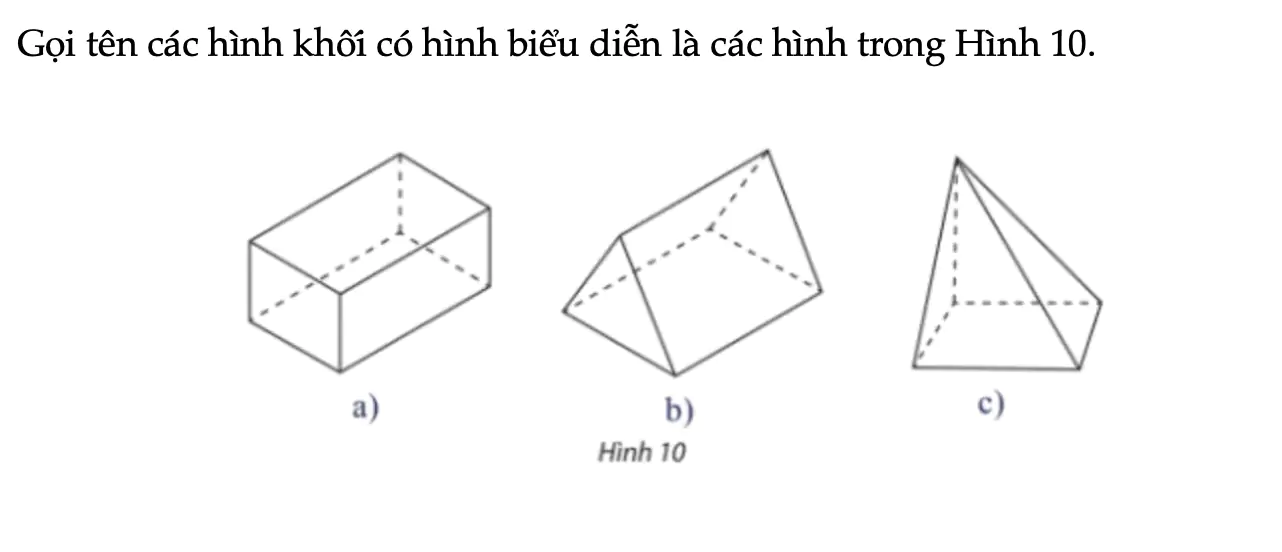
Gọi tên các hình khối có hình biểu diễn là các hình trong Hình 10.

Vận dụng 3 trang 126 Toán 11 Tập 1
Vẽ hình biểu diễn của một hình chóp tam giác SABC đặt trên một hình lăng trụ tam giác ABC.A’B’C’.
Giải bài tập Bài tập cuối chương 4

Bài 1 trang 127 Toán 11 Tập 1
Cho tam giác ABC. Lấy điểm M trên cạnh AC kéo dài (Hình 1). Mệnh đề nào sau đây là mệnh đề sai. Bài 1 trang 127 Toán 11 Tập 1

Bài 2 trang 127 Toán 11 Tập 1
Cho tứ diện ABCD với I và J lần lượt là trung điểm các cạnh AB và CD. Mệnh đề nào sau đây đúng. Bài 2 trang 127 Toán 11 Tập 1

Bài 3 trang 127 Toán 11 Tập 1
Cho hình chóp SABCD có AC cắt BD tại M, AB cắt CD tại N. Trong các đường thẳng sau đây, đường nào là giao tuyến của (SAC) và (SBD). Bài 3 trang 127 Toán 11 Tập 1
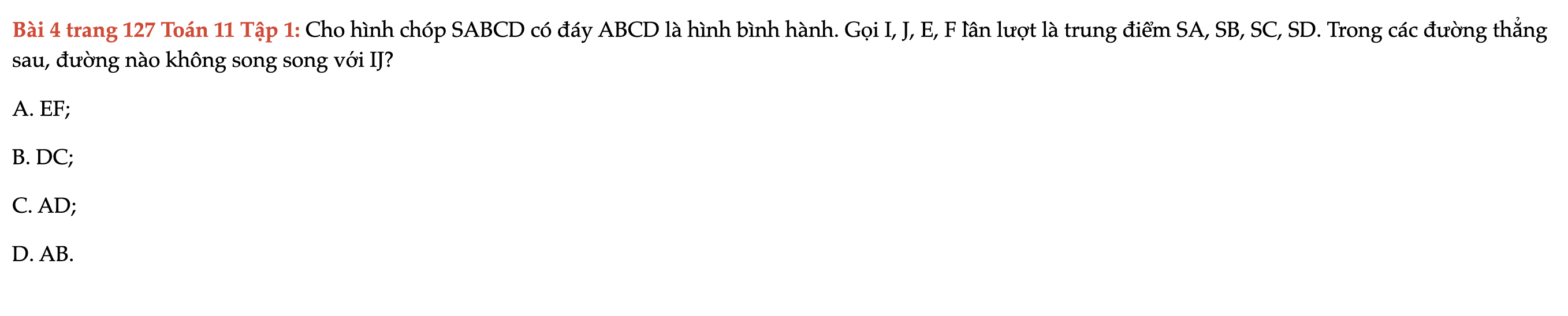
Bài 4 trang 127 Toán 11 Tập 1
Cho hình chóp SABCD có đáy ABCD là hình bình hành. Gọi I, J, E, F lần lượt là trung điểm SA, SB, SC, SD. Trong các đường thẳng sau, đường nào không song song với IJ. Bài 4 trang 127 Toán 11 Tập 1

Bài 5 trang 127 Toán 11 Tập 1
Cho hình bình hành ABCD và một điểm S không nằm trong mặt phẳng (ABCD). Giao tuyến của hai mặt phẳng (SAB) và (SCD) là một đường thẳng song song với đường thẳng nào sau đây. Bài 5 trang 127 Toán 11 Tập 1

Bài 6 trang 127 Toán 11 Tập 1
Cho hình chóp tứ giác đều SABCD có cạnh đáy bằng 10. M là điểm trên SA. Một mặt phẳng (α) đi qua M song song với AB và CD, cắt hình chóp theo một tứ giác có diện tích là. Bài 6 trang 127 Toán 11 Tập 1

Bài 7 trang 127 Toán 11 Tập 1
Quan hệ song song trong không gian có tính chất nào trong các tính chất sau. Bài 7 trang 127 Toán 11 Tập 1

Bài 8 trang 128 Toán 11 Tập 1
Cho hình lăng trụ ABC.A’B’C’. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AC, AA’, A’C’, BC. Bài 8 trang 128 Toán 11 Tập 1

Bài 9 trang 128 Toán 11 Tập 1
Cho hình hộp ABCD.A’B’C’D’. Gọi M và N lần lượt là trung điểm của AB và A’B’ và O là một điểm thuộc miền trong của mặt bên CC’D’D. Tìm giao tuyến của mặt phẳng (OMN) với các mặt của hình hộp. Bài 9 trang 128 Toán 11 Tập 1

Bài 10 trang 128 Toán 11 Tập 1
Cho hình chóp SABCD với ABCD là hình thoi cạnh a, tam giác SAD đều. M là điểm trên cạnh AB, (α) là mặt phẳng qua M và (α) // (SAD) cắt CD, SC, SD lần lượt tại N, P, Q. Bài 10 trang 128 Toán 11 Tập 1

Bài 11 trang 128 Toán 11 Tập 1
Cho mặt phẳng (α) và hai đường thẳng chéo nhau a, b cắt (α) tại A và B. Gọi d là đường thẳng thay đổi luôn luôn song song với (α) và cắt a tại M, cắt b tại N. Qua điểm N dựng đường thẳng song song với a cắt (α) tại điểm C. Bài 11 trang 128 Toán 11 Tập 1

Bài 12 trang 128 Toán 11 Tập 1
Cho hai hình bình hành ABCD và ABEF nằm trong hai mặt phẳng hoàn toàn khác nhau. Lấy các điểm M, N lần lượt thuộc các đường chéo AC và BF sao cho MC = 2MA; NF = 2NB. Bài 12 trang 128 Toán 11 Tập 1