Công thức đạo hàm | SGK Toán 12 - Cánh diều
Công thức đạo hàm hay và đầy đủ nhất, công thức đạo hàm tính nhanh, công thức đạo hàm hàm đa thức, hàm căn thức, hàm phân thức hữu tỉ, hàm lượng giác, hàm mũ, hàm loga, hàm hợp
Dưới đây là công thức Công thức đạo hàm
BẢNG CÔNG THỨC TÍNH ĐẠO HÀM
A. Đạo hàm của tổng, hiệu, tích, thương của hàm số
B. Đạo hàm của hàm hợp
Cho hàm số 
. Khi đó, 
.
Ví dụ: 
có đạo hàm là 
.
C. Đạo hàm của các hàm sơ cấp cơ bản
D. Đạo hàm của hàm mũ, hàm logarit
E. Đạo hàm của hàm phân thức hửu tỉ
Một số bài tập ứng dụng công thức Công thức đạo hàm:
Bài 9.6 trang 94 Toán 11 Tập 2
Tính đạo hàm của các hàm số sau:
a) y = x3 – 3x2 + 2x + 1;
b)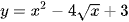 
.
;
.Bài 9.8 trang 94 Toán 11 Tập 2
Tính đạo hàm của các hàm số sau:
a) y = xsin2x;
b) y = cos2x + sin2x;
c) y = sin3x – 3sinx;
d) y = tanx + cotx.
Bài 9.9 trang 94 Toán 11 Tập 2
Tính đạo hàm các hàm số sau:
a) 
;
b) y = log3(4x + 1).
Bài 9.10 trang 94 Toán 11 Tập 2
Cho hàm số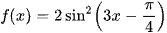 
. Chứng minh rằng |f'(x)| ≤ 6 với mọi x.
Bài 9.11 trang 94 Toán 11 Tập 2
Một vật chuyển động rơi tự do có phương trình h(t) = 100 – 4,9t2, ở đó độ cao h so với mặt đất tính bằng mét và thời gian t tính bằng giây. Tính vận tốc của vật:
a) Tại thời điểm t = 5 giây;
b) Khi vật chạm đất.
Bài 9.12 trang 94 Toán 11 Tập 2
Chuyển động của một hạt trên một dây rung được cho bởi s(t) = 12 + 0,5sin(4πt), trong đó s tính bằng centimét và t tính bằng giây. Tính vận tốc của hạt sau t giây. Vận tốc cực đại của hạt là bao nhiêu?
Bài 9.14 trang 96 Toán 11 Tập 2
Tính đạo hàm cấp hai của các hàm số sau:
a) y = ln(x + 1);
b) y = tan2x.
Bài 9.15 trang 96 Toán 11 Tập 2
Cho hàm số P(x) = ax2 + bx + 3 (a, b là hằng số). Tìm a, b biết P'(1) = 0 và P''(1) = –2.