Giải bài tập Thực hành 1 trang 35 Toán 11 Tập 1 | Toán 11 - Chân trời sáng tạo
Hướng dẫn giải chi tiết từng bước bài tập Thực hành 1 trang 35 Toán 11 Tập 1. Bài 5: Phương trình lượng giác cơ bản. Toán 11 - Chân trời sáng tạo
Đề bài:
Chỉ ra lỗi sai trong phép biến đổi phương trình dưới đây:
Đáp án và cách giải chi tiết:
Lỗi sai: Phương trình x2 = 2x và phương trình không tương đương vì:
Phương trình x2 = 2x có tập nghiệm S1 = {0; 2}.
Phương trình có tập nghiệm S2 = {2}.
Nguồn: loigiaitoan.com
Tổng số đánh giá:
Xếp hạng: / 5 sao
Bài tập liên quan:
Bài 1 trang 40 Toán 11 Tập 1
Bài 1 trang 40 Toán 11 Tập 1: Giải các phương trình lượng giác sau:
a)
b)
c)
Bài 3 trang 41 Toán 11 Tập 1
Bài 3 trang 41 Toán 11 Tập 1: Giải các phương trình lượng giác sau:
a) tanx = tan55°;
b) .
Bài 5 trang 41 Toán 11 Tập 1
Bài 5 trang 41 Toán 11 Tập 1: Tại các giá trị nào của x thì đồ thị hàm số y = cosx và y = sinx giao nhau?
Hoạt động khởi động trang 34 Toán 11 Tập 1
Trong hình bên, khi bàn đạp xe đạp quay, bóng M của đầu trục quay dao động trên mặt đất quanh điểm O theo phương trình s = 17cos5πt với s (cm) là tọa độ của điểm M trên trục Ox và t (giây) là thời gian bàn đạp quay. Làm cách nào để xác định được các thời điểm mà tại đó độ dài bóng OM bằng 10cm?

Hoạt động khám phá 2 trang 35 Toán 11 Tập 1
a) Có giá trị nào của x để sinx = 1,5 không?
b) Trong Hình 1, những điểm nào trên đường tròn lượng giác biểu diễn góc lượng giác x có sinx = 0,5? Xác định số đo của các góc lượng giác đó.

Hoạt động khám phá 3 trang 36 Toán 11 Tập 1
Trong Hình 3, những điểm nào trên đường tròn lượng giác biểu diễn diễn góc lượng giác x có cosx = ? Xác định số đo của các góc lượng giác đó.

Thực hành 3 trang 37 Toán 11 Tập 1
Giải các phương trình sau:
a) cosx = – 3;
b) cosx = cos15°;
c) .
Thực hành 4 trang 38 Toán 11 Tập 1
Giải các phương trình sau:
a) tanx = 0;
b) tan(30° – 3x) = tan75°.
Hoạt động khám phá 5 trang 38 Toán 11 Tập 1
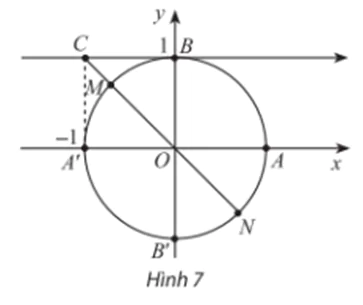
Trong mặt phẳng tọa độ Oxy, cho C là điểm trên trục côtang có tọa độ là (– 1; 1) (Hình 7). Những điểm nào biểu diễn góc lượng giác x có cotx = – 1? Xác định số đo của các góc lượng giác đó.
Thực hành 5 trang 39 Toán 11 Tập 1
Giải các phương trình sau:
a) cotx = 1;
b) cot(3x + 30°) = cot75°.
Vận dụng trang 40 Toán 11 Tập 1
Quay lại bài toán khởi động, phương trình chuyển động của bóng đầu trục bàn đạp là x = 17cos5πt (cm) với t được đo bằng giây. Xác định các thời điểm t mà tại đó độ dài bóng |x| bằng 10 cm. Làm tròn kết quả đến hàng phần mười.
Bài 2 trang 40 Toán 11 Tập 1
Bài 2 trang 40 Toán 11 Tập 1: Giải các phương trình lượng giác sau:
a)  ;
;
b)  ;
;
c) cos2x = 1.
Bài 4 trang 41 Toán 11 Tập 1
Bài 4 trang 41 Toán 11 Tập 1: Giải các phương trình lượng giác sau:
a)  ;
;
b)  .
.
Bài 6 trang 41 Toán 11 Tập 1
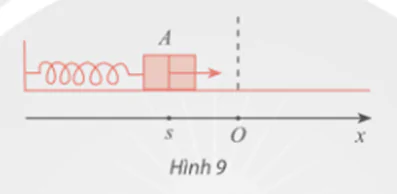
Bài 6 trang 41 Toán 11 Tập 1: Trong Hình 9, khi được kéo ra khỏi vị trí cân bằng ở điểm O và buông tay, lực đàn hồi của lò xo khiến vật A gắn ở đầu của lò xo dao động quanh O. Tọa độ s (cm) của A trên trục Ox vào thời điểm t (giây) sau khi buông tay được xác định bởi công thức  . Vào các thời điểm nào thì
. Vào các thời điểm nào thì  cm?
cm?
(Theo https://www.britannica.com/science/simple-harmonic-motion)
Bài 7 trang 41 Toán 11 Tập 1
Bài 7 trang 41 Toán 11 Tập 1: Trong Hình 10, ngọn đèn hải đăng H cách bờ biển yy’ một khoảng HO = 1km. Đèn xoay ngược chiều kim đồng hồ với tốc độ rad/s và chiếu hai luồng ánh sáng về hai phía đối diện nhau. Khi đèn xoay, điểm M mà luồng ánh sáng của hải đăng rọi vào bờ biển chuyển động dọc theo bờ.
(Theo https://www.mnhs.org/splitrock/learn/technology)

a) Ban đầu luồng sáng trùng với đường thẳng HO. Viết hàm số biểu thị tọa độ yM của điểm M trên trục Oy theo thời gian t.
b) Ngôi nhà N nằm trên bờ biển với tọa độ yS = – 1 (km). Xác định các thời điểm t mà đèn hải đăng chiếu vào ngôi nhà.
Hoạt động khám phá 1 trang 34 Toán 11 Tập 1
Xác định và so sánh tập nghiệm của các phương trình sau:
a) x – 1 = 0;
b) x2 – 1 = 0;
c)  .
.
Thực hành 2 trang 36 Toán 11 Tập 1
Giải các phương trình sau:
a)  ;
;
b) sin(x + 30°) = sin(x + 60°).
Hoạt động khám phá 4 trang 37 Toán 11 Tập 1
Trong mặt phẳng tọa độ Oxy, cho T là điểm trên trục tang có tọa độ là  (Hình 5). Những điểm nào trên đường tròn lượng giác biểu diễn góc lượng giác x có
(Hình 5). Những điểm nào trên đường tròn lượng giác biểu diễn góc lượng giác x có  ? Xác định số đo của các góc lượng giác đó.
? Xác định số đo của các góc lượng giác đó.
Thực hành 6 trang 40 Toán 11 Tập 1
Sử dụng máy tính cầm tay để giải các phương trình sau:
a) cosx = 0,4;
b)  .
.