Giải bài tập Toán 11 Chương 8: Quan hệ vuông góc trong không gian. Phép chiếu vuông góc | Cánh Diều
Hướng dẫn giải Chương 8: Quan hệ vuông góc trong không gian. Phép chiếu vuông góc
Giải bài tập Bài 1: Hai đường thẳng vuông góc

Bài 1 trang 79 Toán 11 Tập 2
Hình 6 gợi nên hình ảnh 5 cặp đường thẳng vuông góc. Hãy chỉ ra 5 cặp đường thẳng đó. Bài 1 trang 79 Toán 11 Tập 2

Bài 2 trang 79 Toán 11 Tập 2
Trong Hình 7 cho ABB’A’, BCC’B’, ACC’A’ là các hình chữ nhật. Chứng minh rằng AB ⊥ CC’, AA’ ⊥ BC. Bài 2 trang 79 Toán 11 Tập 2

Bài 3 trang 79 Toán 11 Tập 2
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và góc SAB = 100° (Hình 8). Tính góc giữa hai đường thẳng SA và AB. Bài 3 trang 79 Toán 11 Tập 2

Bài 4 trang 79 Toán 11 Tập 2
Bạn Hoa nói rằng: “Nếu hai đường thẳng phân biệt a và b cùng vuông góc với đường thẳng c thì a và b vuông góc với nhau”. Bạn Hoa nói đúng hay sai? Vì sao? Bài 4 trang 79 Toán 11 Tập 2

Câu hỏi khởi động trang 77 Toán 11 Tập 2
Trong Hình 1, hai đường thẳng a, b gợi nên hình ảnh hai đường thẳng vuông góc trong không gian. Trong không gian, thế nào là hai đường thẳng vuông góc với nhau? Câu hỏi khởi động trang 77 Toán 11 Tập 2

Hoạt động 1 trang 77 Toán 11 Tập 2
Trong mặt phẳng cho hai đường thẳng a, b. Nếu a và b cắt nhau tại điểm O (Hình 2) thì góc giữa hai đường thẳng a, b được xác định như thế nào? Hoạt động 1 trang 77 Toán 11 Tập 2

Luyện tập 1 trang 78 Toán 11 Tập 2
Cho tứ diện ABCD có M, N, P lần lượt là trung điểm của AB, BC, DA. Biết tam giác MNP đều. Tính góc giữa hai đường thẳng AC và BD. Luyện tập 1 trang 78 Toán 11 Tập 2

Hoạt động 2 trang 78 Toán 11 Tập 2
Trong Hình 1 ở phần mở đầu, hai đường thẳng a, b gợi nên hình ảnh hai đường thẳng vuông góc. Góc giữa a và b bằng bao nhiêu độ? Hoạt động 2 trang 78 Toán 11 Tập 2
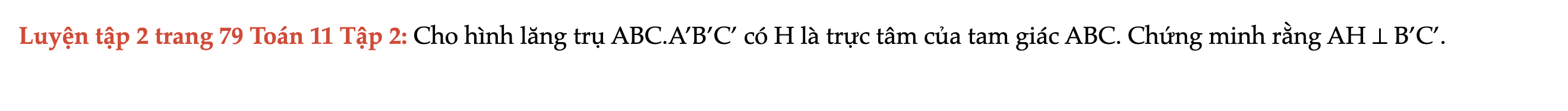
Luyện tập 2 trang 79 Toán 11 Tập 2
Cho hình lăng trụ ABC.A’B’C’ có H là trực tâm của tam giác ABC. Chứng minh rằng AH ⊥ B’C’. Luyện tập 2 trang 79 Toán 11 Tập 2
Giải bài tập Bài 2: Đường thẳng vuông góc với mặt phẳng

Bài 1 trang 88 Toán 11 Tập 2
Quan sát Hình 30 (hai cột của biển báo, mặt đường), cho biết hình đó gợi nên tính chất nào về quan hệ vuông góc giữa đường thẳng và mặt phẳng. Bài 1 trang 88 Toán 11 Tập 2

Bài 2 trang 88 Toán 11 Tập 2
Cho hình chóp S.ABC. Gọi H là hình chiếu của S trên mặt phẳng (ABC). Xác định hình chiếu của các đường thẳng SA, SB, SC trên mặt phẳng (ABC). Bài 2 trang 88 Toán 11 Tập 2

Bài 3 trang 88 Toán 11 Tập 2
Cho tứ diện ABCD có AB ⊥ (BCD), các tam giác BCD và ACD là những tam giác nhọn. Gọi H, K lần lượt là trực tâm của các tam giác BCD, ACD (Hình 31). Chứng minh rằng CD ⊥ (ABH). Bài 3 trang 88 Toán 11 Tập 2

Bài 4 trang 88 Toán 11 Tập 2
Cho hình chóp S.ABCD có đáy là hình bình hành. Tam giác ABC nhọn có trực tâm H là hình chiếu của S trên (ABCD). Chứng minh rằng SA ⊥ AD. Bài 4 trang 88 Toán 11 Tập 2
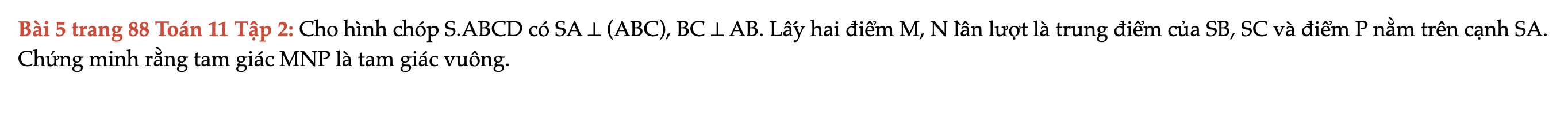
Bài 5 trang 88 Toán 11 Tập 2
Cho hình chóp S.ABCD có SA ⊥ (ABC), BC ⊥ AB. Lấy hai điểm M, N lần lượt là trung điểm của SB, SC và điểm P nằm trên cạnh SA. Chứng minh rằng tam giác MNP là tam giác vuông. Bài 5 trang 88 Toán 11 Tập 2

Câu hỏi khởi động trang 80 Toán 11 Tập 2
Trong Hình 9, cột gỗ thẳng đứng và sàn nhà nằm ngang gợi nên hình ảnh đường thẳng vuông góc với mặt phẳng. Câu hỏi khởi động trang 80 Toán 11 Tập 2

Hoạt động 1 trang 80 Toán 11 Tập 2
Hình 10 mô tả một người thợ xây đang thả dây dọi vuông góc với nền nhà. Coi dây dọi như đường thẳng d và nền nhà như mặt phẳng (P), khi đó Hình 10 gợi nên hình ảnh đường thẳng d vuông góc với mặt phẳng (P). Hoạt động 1 trang 80 Toán 11 Tập 2

Hoạt động 2 trang 81 Toán 11 Tập 2
Hình 12 mô tả cửa tròn xoay, ở đó trục cửa và hai mép cửa gợi nên hình ảnh các đường thẳng d, a, b; sàn nhà coi như mặt phẳng (P) chứa a và b. Hoạt động 2 trang 81 Toán 11 Tập 2

Luyện tập 1 trang 81 Toán 11 Tập 2
Cho hình chóp S.ABCD có đáy ABCD là hình thoi, SA ⊥ (ABCD). Chứng minh rằng BD ⊥ (SAC). Luyện tập 1 trang 81 Toán 11 Tập 2

Hoạt động 3 trang 81 Toán 11 Tập 2
Cho điểm O và đường thẳng a. Gọi b, c là hai đường thẳng phân biệt cùng đi qua điểm O và cùng vuông góc với đường thẳng a (Hình 14). Hoạt động 3 trang 81 Toán 11 Tập 2

Luyện tập 2 trang 81 Toán 11 Tập 2
Hình 17 mô tả một cửa gỗ có dạng hình chữ nhật, ở đó nẹp cửa và mép dưới cửa lần lượt gợi nên hình ảnh hai đường thẳng d và a. Điểm M là vị trí giao giữa mép gắn bản lề và mép dưới của cửa. Luyện tập 2 trang 81 Toán 11 Tập 2

Hoạt động 4 trang 82 Toán 11 Tập 2
Cho mặt phẳng (P) và điểm O. Gọi a, b là hai đường thẳng cắt nhau thuộc mặt phẳng (P) sao cho a và b không đi qua O. Lấy hai mặt phẳng (Q), (R) lần lượt đi qua O và vuông góc a, b (Hình 18). Hoạt động 4 trang 82 Toán 11 Tập 2
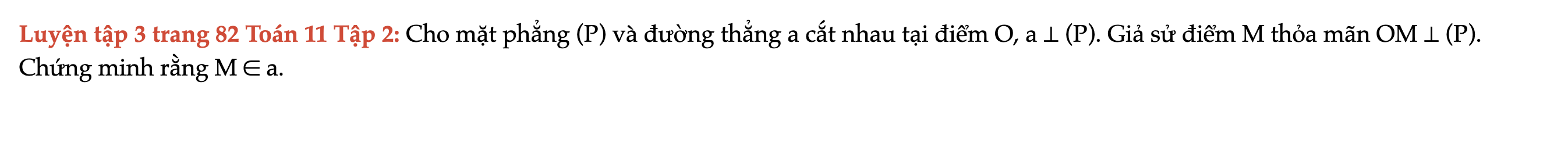
Luyện tập 3 trang 82 Toán 11 Tập 2
Cho mặt phẳng (P) và đường thẳng a cắt nhau tại điểm O, a ⊥ (P). Giả sử điểm M thỏa mãn OM ⊥ (P). Chứng minh rằng M ∈ a. Luyện tập 3 trang 82 Toán 11 Tập 2

Hoạt động 5 trang 83 Toán 11 Tập 2
Trong Hình 19, hai thanh sắt và bản phẳng để ngồi gợi nên hình ảnh hai đường thẳng a, b và mặt phẳng (P). Hoạt động 5 trang 83 Toán 11 Tập 2
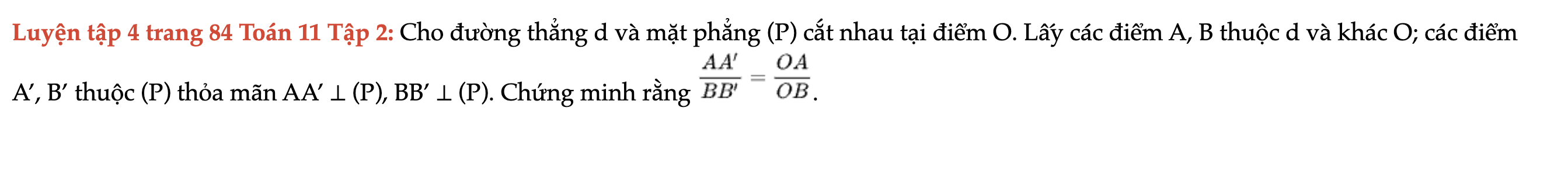
Luyện tập 4 trang 84 Toán 11 Tập 2
Cho đường thẳng d và mặt phẳng (P) cắt nhau tại điểm O. Lấy các điểm A, B thuộc d và khác O; các điểm A’, B’ thuộc (P) thỏa mãn AA’ ⊥ (P), BB’ ⊥ (P). Luyện tập 4 trang 84 Toán 11 Tập 2

Hoạt động 6 trang 84 Toán 11 Tập 2
Trong Hình 21, hai mặt trần của nhà cao tầng và cột trụ bê tông gợi nên hình ảnh hai mặt phẳng (P), (Q) phân biệt và đường thẳng a. Hoạt động 6 trang 84 Toán 11 Tập 2

Luyện tập 5 trang 85 Toán 11 Tập 2
Cho hình chóp S.ABC có SA ⊥ (ABC). Mặt phẳng (P) khác với mặt phẳng (ABC), vuông góc với đường thẳng SA và lần lượt cắt các đường thẳng SB, SC tại hai điểm phân biệt B’, C’. Chứng minh rằng B’C’ // BC. Luyện tập 5 trang 85 Toán 11 Tập 2

Hoạt động 7 trang 85 Toán 11 Tập 2
Cho mặt phẳng (P). Xét một điểm M tuỳ ý trong không gian. Có bao nhiêu đường thẳng d đi qua điểm M và vuông góc với mặt phẳng (P)? Hoạt động 7 trang 85 Toán 11 Tập 2
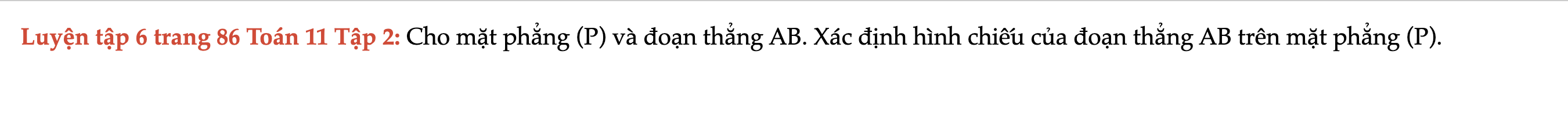
Luyện tập 6 trang 86 Toán 11 Tập 2
Cho mặt phẳng (P) và đoạn thẳng AB. Xác định hình chiếu của đoạn thẳng AB trên mặt phẳng (P). Luyện tập 6 trang 86 Toán 11 Tập 2

Hoạt động 8 trang 87 Toán 11 Tập 2
Trong Hình 27, mặt sàn gợi nên hình ảnh mặt phẳng (P), đường thẳng a không vuông góc với mặt phẳng (P), đường thẳng a’ là hình chiếu của đường thẳng a trên mặt phẳng (P), đường thẳng d nằm trong mặt phẳng (P). Hoạt động 8 trang 87 Toán 11 Tập 2

Luyện tập 7 trang 87 Toán 11 Tập 2
Cho hình chóp S.ABCD có SA ⊥ (ABCD) và đáy ABCD là hình chữ nhật. Chứng minh rằng các tam giác SBC và SCD là các tam giác vuông. Luyện tập 7 trang 87 Toán 11 Tập 2
Giải bài tập Bài 3: Góc giữa đường thẳng và mặt phẳng. Góc nhị diện

Bài 1 trang 94 Toán 11 Tập 2
Cho hình chóp S.ABCD có SA ⊥ (ABCD), đáy ABCD là hình thoi cạnh a và AC = a. Tính số đo của góc nhị diện [B, SA, C]. Bài 1 trang 94 Toán 11 Tập 2

Bài 2 trang 94 Toán 11 Tập 2
Cho hình chóp S.ABCD có đáy ABCD là hình vuông, hai đường thẳng AC và BD cắt nhau tại O, SO ⊥ (ABCD), tam giác SAC là tam giác đều. Tính số đo của góc giữa đường thẳng SA và mặt phẳng (ABCD). Bài 2 trang 94 Toán 11 Tập 2

Bài 3 trang 94 Toán 11 Tập 2
Dốc là đoạn đường thẳng nối hai khu vực hay hai vùng có độ cao khác nhau. Độ dốc được xác định bằng góc giữa dốc và mặt phẳng nằm ngang, ở đó độ dốc lớn nhất là 100%, tương ứng với góc 90° (độ dốc 10% tương ứng với góc 9°). Bài 3 trang 94 Toán 11 Tập 2

Bài 4 trang 94 Toán 11 Tập 2
Trong Hình 42, máy tính xách tay đang mở gợi nên hình ảnh của một góc nhị diện. Ta gọi số đo góc nhị diện đó là độ mở của màn hình máy tính. Tính độ mở của màn hình máy tính đó. Bài 4 trang 94 Toán 11 Tập 2

Bài 5 trang 94 Toán 11 Tập 2
Bài 5 trang 94 Toán 11 Tập 2

Bài 6 trang 94 Toán 11 Tập 2
Cho hình chóp S.ABC có SA ⊥ (ABC). Gọi α là số đo của góc nhị diện [A, BC, S]. Chứng minh rằng tỉ số diện tích của hai tam giác ABC và SBC bằng cosα. Bài 6 trang 94 Toán 11 Tập 2

Câu hỏi khởi động trang 89 Toán 11 Tập 2
Hình 32 biểu diễn một chiếc gậy dựa vào tường. Bạn Hoa nói góc nghiêng giữa chiếc gậy và mặt đất bằng 65°. Câu hỏi khởi động trang 89 Toán 11 Tập 2

Hoạt động 1 trang 89 Toán 11 Tập 2
Quan sát Hình 32 và cho biết. Hình chiếu của đường thẳng MO trên mặt phẳng (P) là đường thẳng nào. Hoạt động 1 trang 89 Toán 11 Tập 2

Luyện tập 1 trang 90 Toán 11 Tập 2
Giả sử ở những giây đầu tiên sau khi cất cánh, máy bay chuyển động theo một đường thẳng tạo với mặt đất một góc 20° và có tốc độ 200 km/h. Luyện tập 1 trang 90 Toán 11 Tập 2

Hoạt động 2 trang 91 Toán 11 Tập 2
Quan sát hình ảnh một quyển sổ được mở ra (Hình 35), mỗi trang sổ gợi nên hình ảnh của một nửa mặt phẳng. Nêu đặc điểm của hai nửa mặt phẳng đó. Hoạt động 2 trang 91 Toán 11 Tập 2
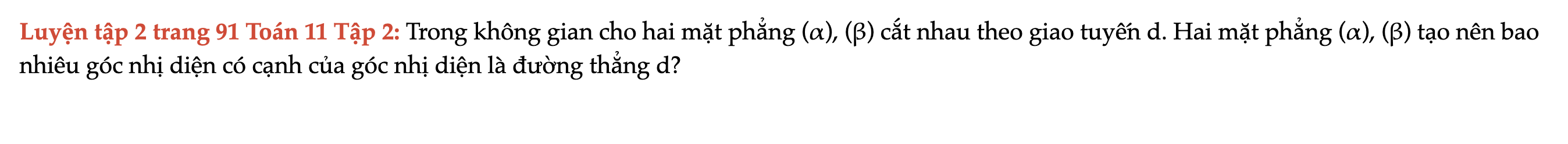
Luyện tập 2 trang 91 Toán 11 Tập 2
Trong không gian cho hai mặt phẳng (α), (β) cắt nhau theo giao tuyến d. Hai mặt phẳng (α), (β) tạo nên bao nhiêu góc nhị diện có cạnh của góc nhị diện là đường thẳng d? Luyện tập 2 trang 91 Toán 11 Tập 2

Hoạt động 3 trang 92 Toán 11 Tập 2
Cho góc nhị diện có hai mặt là hai nửa mặt phẳng (P), (Q) và cạnh của góc nhị diện là đường thẳng d. Hoạt động 3 trang 92 Toán 11 Tập 2

Luyện tập 3 trang 93 Toán 11 Tập 2
Cho hình chóp S.ABCD có đáy ABCD là hình vuông và SA ⊥ (ABCD). Tính số đo của mỗi góc nhị diện sau. Luyện tập 3 trang 93 Toán 11 Tập 2
Giải bài tập Bài 4: Hai mặt phẳng vuông góc

Bài 1 trang 99 Toán 11 Tập 2
Quan sát ba mặt phẳng (P), (Q), (R) ở Hình 57, chỉ ra hai cặp mặt phẳng mà mỗi cặp gồm hai mặt phẳng vuông góc với nhau. Hãy sử dụng kí hiệu để viết những kết quả đó. Bài 1 trang 99 Toán 11 Tập 2
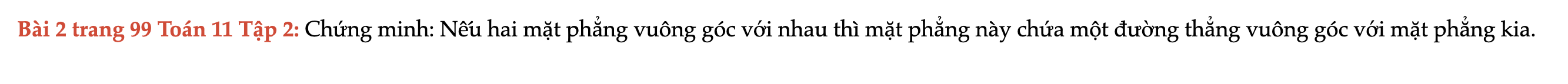
Bài 2 trang 99 Toán 11 Tập 2
Chứng minh: Nếu hai mặt phẳng vuông góc với nhau thì mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng kia. Bài 2 trang 99 Toán 11 Tập 2

Bài 3 trang 99 Toán 11 Tập 2
Chứng minh các định lí sau. Bài 3 trang 99 Toán 11 Tập 2

Bài 4 trang 99 Toán 11 Tập 2
Cho một đường thẳng không vuông góc với mặt phẳng cho trước. Chứng minh rằng tồn tại duy nhất một mặt phẳng chứa đường thẳng đó và vuông góc với mặt phẳng đã cho. Bài 4 trang 99 Toán 11 Tập 2

Bài 5 trang 99 Toán 11 Tập 2
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, mặt phẳng (SAB) vuông góc với mặt đáy, tam giác SAB vuông cân tại S. Gọi M là trung điểm của AB. Chứng minh rằng SM ⊥ (ABCD). Bài 5 trang 99 Toán 11 Tập 2

Bài 6 trang 99 Toán 11 Tập 2
Cho hình lăng trụ ABC.A’B’C’ có tất cả các cạnh cùng bằng a, hai mặt phẳng (A’AB) và (A’AC) cùng vuông góc với (ABC). Chứng minh rằng AA’ ⊥ (ABC). Bài 6 trang 99 Toán 11 Tập 2

Câu hỏi khởi động trang 95 Toán 11 Tập 2
Để công trình xây dựng được an toàn và bền vững, người ta thường xây tường nhà vuông góc với nền nhà (Hình 44). Câu hỏi khởi động trang 95 Toán 11 Tập 2

Hoạt động 1 trang 95 Toán 11 Tập 2
Hai vách ngăn tủ trong Hình 45 gợi nên hình ảnh hai mặt phẳng (P) và (Q) cắt nhau tạo nên bốn góc nhị diện. Các góc nhị diện đó có phải là góc nhị diện vuông hay không? Hoạt động 1 trang 95 Toán 11 Tập 2

Luyện tập 1 trang 95 Toán 11 Tập 2
Nêu ví dụ trong thực tiễn minh họa hình ảnh hai mặt phẳng vuông góc. Luyện tập 1 trang 95 Toán 11 Tập 2

Hoạt động 2 trang 96 Toán 11 Tập 2
Nền nhà, cánh cửa và mép cánh cửa ở Hình 48 gợi nên hình ảnh mặt phẳng (P), mặt phẳng (Q) và đường thẳng a nằm trên mặt phẳng (P). Hoạt động 2 trang 96 Toán 11 Tập 2
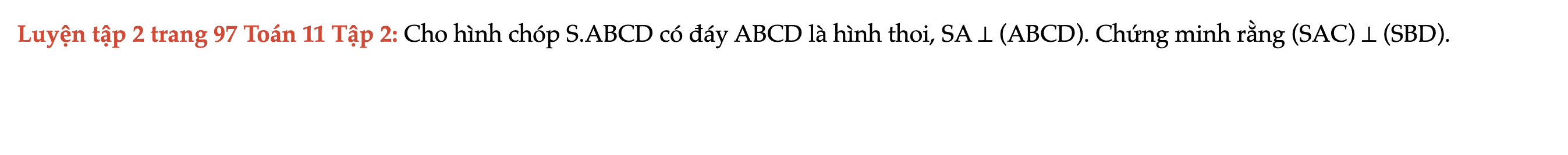
Luyện tập 2 trang 97 Toán 11 Tập 2
Cho hình chóp S.ABCD có đáy ABCD là hình thoi, SA ⊥ (ABCD). Chứng minh rằng (SAC) ⊥ (SBD). Luyện tập 2 trang 97 Toán 11 Tập 2

Hoạt động 3 trang 97 Toán 11 Tập 2
Cho hình chóp S.OAB thoả mãn (AOS) ⊥ (AOB), góc AOS = góc AOB = 90° (Hình 51). Hoạt động 3 trang 97 Toán 11 Tập 2

Luyện tập 3 trang 97 Toán 11 Tập 2
Cho tứ diện ABCD có (ABD) ⊥ (BCD) và CD ⊥ BD. Chứng minh rằng tam giác ACD vuông. Luyện tập 3 trang 97 Toán 11 Tập 2

Hoạt động 4 trang 98 Toán 11 Tập 2
Trong Hình 54, hai bìa của cuốn sách gợi nên hình ảnh hai mặt phẳng vuông góc với mặt bàn. Hãy dự đoán xem gáy sách có vuông góc với mặt bàn hay không. Hoạt động 4 trang 98 Toán 11 Tập 2

Luyện tập 4 trang 99 Toán 11 Tập 2
Cho hình chóp S.ABC có SA ⊥ SB, SB ⊥ SC, SC ⊥ SA. Chứng minh rằng (SAB) ⊥ (SBC). Luyện tập 4 trang 99 Toán 11 Tập 2
Giải bài tập Bài 5: Khoảng cách

Bài 1 trang 106 Toán 11 Tập 2
Hình 76 gợi nên hình ảnh hai mặt phẳng (P) và (Q) song song với nhau. Cột gỗ cao 4,2 m. Khoảng cách giữa (P) và (Q) là bao nhiêu mét? Bài 1 trang 106 Toán 11 Tập 2

Bài 2 trang 106 Toán 11 Tập 2
Cho hình tứ diện ABCD có AB = a, BC = b, BD = c, góc ABC = ABD = BCD = 90°. Gọi M, N, P lần lượt là trung điểm của AB, AC, AD (Hình 77). Bài 2 trang 106 Toán 11 Tập 2

Bài 3 trang 106 Toán 11 Tập 2
Với giả thiết ở Bài tập 2, hãy chứng minh rằng MN // BC. Tính khoảng cách giữa hai đường thẳng MN và BC. Bài 3 trang 106 Toán 11 Tập 2

Bài 4 trang 106 Toán 11 Tập 2
Cho hình chóp S.ABCD có SA ⊥ (ABCD), đáy ABCD là hình vuông cạnh a, SA = a (Hình 78). Tính khoảng cách từ điểm S đến đường thẳng CD. Bài 4 trang 106 Toán 11 Tập 2

Bài 5 trang 106 Toán 11 Tập 2
Với giả thiết ở Bài tập 4, hãy chứng minh rằng BC // (SAD) và tính khoảng cách giữa BC và mặt phẳng (SAD). Bài 5 trang 106 Toán 11 Tập 2

Câu hỏi khởi động trang 100 Toán 11 Tập 2
Hình 58 mô tả cách đo chiều cao của một người khi kiểm tra sức khỏe. Coi mặt bản sắt người đó đứng lên là mặt phẳng (P), mặt bản sắt áp vào đầu người đó là mặt phẳng (Q) song song với (P). Câu hỏi khởi động trang 100 Toán 11 Tập 2

Hoạt động 1 trang 101 Toán 11 Tập 2
Khi lắp thiết bị cho nhà bạn Nam, bác thợ khoan tường tại vị trí M trên tường có độ cao so với nền nhà là MH = 80 cm. Hoạt động 1 trang 101 Toán 11 Tập 2

Luyện tập 1 trang 101 Toán 11 Tập 2
Cho hình chóp S.ABC có SA ⊥ (ABC), AI ⊥ BC (I ∈ BC), AH ⊥ SI (H ∈ SI). Chứng minh rằng khoảng cách từ A đến mặt phẳng (SBC) bằng AH. Luyện tập 1 trang 101 Toán 11 Tập 2

Hoạt động 2 trang 102 Toán 11 Tập 2
Trong Hình 64, hai mép của con đường gợi nên hình ảnh hai đường thẳng song song Δ và ∆’. Xét điểm A trên đường thẳng Δ. Hoạt động 2 trang 102 Toán 11 Tập 2

Luyện tập 2 trang 102 Toán 11 Tập 2
Người ta dựng các cột đèn vuông góc với mặt đường, trong đó mỗi cột đèn gợi nên hình ảnh một đường thẳng. Khoảng cách giữa hai chân cột đèn liên tiếp đo được là 5 m. Luyện tập 2 trang 102 Toán 11 Tập 2

Hoạt động 3 trang 102 Toán 11 Tập 2
Trong Hình 67, thanh gỗ dọc phía trên các cột và mặt đường hành lang gợi nên hình ảnh đường thẳng Δ và mặt phẳng (P) song song với nhau, chiều cao của chiếc cột có đỉnh cột A là khoảng cách từ điểm A đến mặt phẳng (P). Hoạt động 3 trang 102 Toán 11 Tập 2
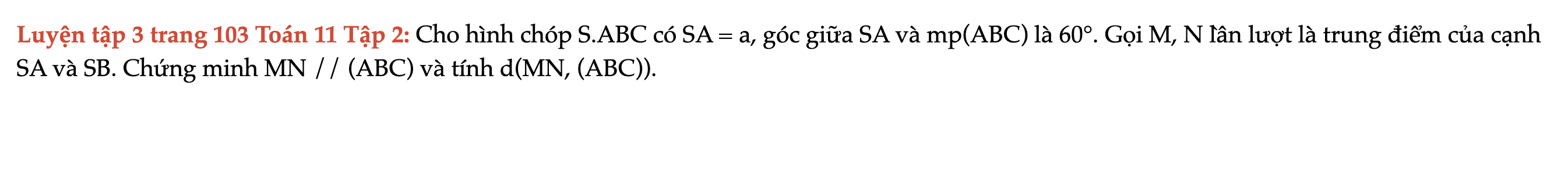
Luyện tập 3 trang 103 Toán 11 Tập 2
Cho hình chóp S.ABC có SA = a, góc giữa SA và mp(ABC) là 60°. Gọi M, N lần lượt là trung điểm của cạnh SA và SB. Chứng minh MN // (ABC) và tính d(MN, (ABC)). Luyện tập 3 trang 103 Toán 11 Tập 2

Hoạt động 4 trang 103 Toán 11 Tập 2
Trong Hình 70, sàn nhà và trần nhà của căn phòng gợi nên hình ảnh hai mặt phẳng song song (P), (Q). Chiều cao của căn phòng là 3 m. Hoạt động 4 trang 103 Toán 11 Tập 2

Luyện tập 4 trang 104 Toán 11 Tập 2
Cho hình lăng trụ ABC.A’B’C’ có cạnh bên bằng a, góc giữa đường thẳng AA’ và mặt phẳng (ABC) bằng 60°. Tính khoảng cách giữa hai mặt phẳng (ABC) và (A’B’C’). Luyện tập 4 trang 104 Toán 11 Tập 2

Hoạt động 5 trang 104 Toán 11 Tập 2
Trong Hình 73, khuôn cửa phía trên và mép cánh cửa phía dưới gợi nên hình ảnh hai đường thẳng a và b chéo nhau, hai bản lề của cánh cửa nằm trên đường thẳng c. Hoạt động 5 trang 104 Toán 11 Tập 2
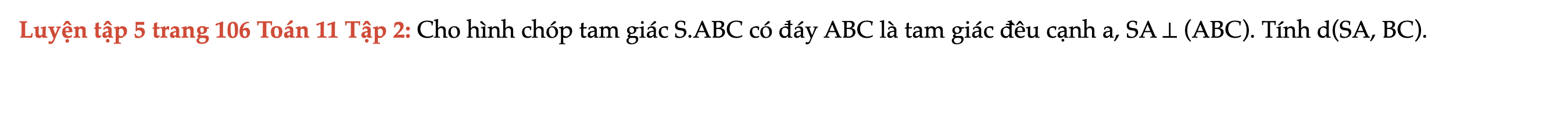
Luyện tập 5 trang 106 Toán 11 Tập 2
Cho hình chóp tam giác S.ABC có đáy ABC là tam giác đều cạnh a, SA ⊥ (ABC). Tính d(SA, BC). Luyện tập 5 trang 106 Toán 11 Tập 2
Giải bài tập Bài 6: Hình lăng trụ đứng. Hình chóp đều. Thể tích của một số hình khối

Bài 1 trang 115 Toán 11 Tập 2
Quan sát và cho biết chiếc đèn treo ở Hình 96a, trạm khảo sát trắc địa ở Hình 96b có dạng hình gì? Bài 1 trang 115 Toán 11 Tập 2

Bài 2 trang 115 Toán 11 Tập 2
Cho hình chóp đều S.ABCD có các cạnh bên và các cạnh đáy đều bằng a. Chứng minh rằng các tam giác ASC và BSD là tam giác vuông cân. Bài 2 trang 115 Toán 11 Tập 2

Bài 3 trang 115 Toán 11 Tập 2
Cho hình lăng trụ đứng ABCD.A’B’C’D’ có đáy ABCD là hình vuông cạnh a. Góc giữa đường thẳng AC’ và mặt phẳng (ABCD) bằng 60°. Bài 3 trang 115 Toán 11 Tập 2

Bài 4 trang 115 Toán 11 Tập 2
Một chiếc bánh chưng có dạng khối hộp chữ nhật với kích thước ba cạnh là 15 cm, 15 cm và 6 cm. Tính thể tích của chiếc bánh chưng đó. Bài 4 trang 115 Toán 11 Tập 2

Bài 5 trang 115 Toán 11 Tập 2
Một miếng pho mát có dạng khối lăng trụ đứng với chiều cao 10 cm và đáy là tam giác vuông cân có cạnh góc vuông bằng 12 cm. Tính khối lượng của miếng pho mát theo đơn vị gam. Bài 5 trang 115 Toán 11 Tập 2

Bài 6 trang 115 Toán 11 Tập 2
Một loại đèn đá muối có dạng khối chóp tứ giác đều (Hình 97). Tính theo a thể tích của đèn đá muối đó, giả sử các cạnh đáy và các cạnh bên đều bằng a. Bài 6 trang 115 Toán 11 Tập 2

Bài 7 trang 115 Toán 11 Tập 2
Người ta xây dựng một chân tháp bằng bê tông có dạng khối chóp cụt tứ giác đều (Hình 98). Cạnh đáy dưới dài 5 m, cạnh đáy trên dài 2 m, cạnh bên dài 3 m. Bài 7 trang 115 Toán 11 Tập 2

Câu hỏi khởi động trang 107 Toán 11 Tập 2
Ở lớp 7, ta đã làm quen với hình lăng trụ đứng tam giác và hình lăng trụ đứng tứ giác, tức là những hình lăng trụ đứng có đáy là tam giác hoặc tứ giác. Câu hỏi khởi động trang 107 Toán 11 Tập 2

Hoạt động 1 trang 107 Toán 11 Tập 2
Cho hình lăng trụ tam giác có các mặt bên là hình chữ nhật ở Hình 80a, 80b. Hãy cho biết mỗi cạnh bên của hình lăng trụ đó có vuông góc với các mặt đáy hay không. Hoạt động 1 trang 107 Toán 11 Tập 2
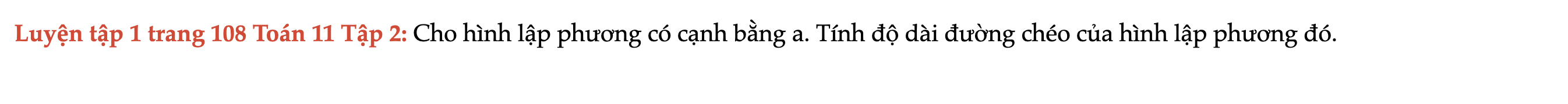
Luyện tập 1 trang 108 Toán 11 Tập 2
Cho hình lập phương có cạnh bằng a. Tính độ dài đường chéo của hình lập phương đó. Luyện tập 1 trang 108 Toán 11 Tập 2

Hoạt động 2 trang 108 Toán 11 Tập 2
Để tạo mô hình một tháp chuông ở Hình 83a từ một tấm bìa hình vuông, bạn Dũng cắt bỏ phần màu trắng gồm bốn tam giác cân bằng nhau có đáy là các cạnh của tấm bìa (Hình 83b). Hoạt động 2 trang 108 Toán 11 Tập 2

Luyện tập 2 trang 110 Toán 11 Tập 2
Cho hình chóp tam giác đều S.ABC. Chứng minh rằng các cạnh bên tạo với mặt phẳng chứa đáy các góc bằng nhau. Luyện tập 2 trang 110 Toán 11 Tập 2
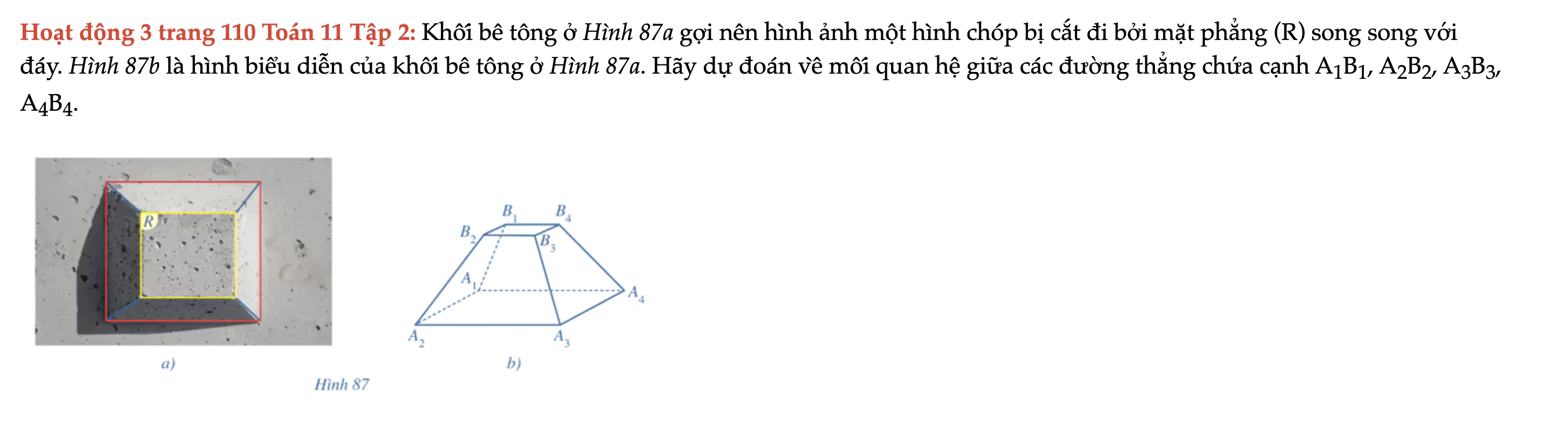
Hoạt động 3 trang 110 Toán 11 Tập 2
Khối bê tông ở Hình 87a gợi nên hình ảnh một hình chóp bị cắt đi bởi mặt phẳng (R) song song với đáy. Hình 87b là hình biểu diễn của khối bê tông ở Hình 87a. Hoạt động 3 trang 110 Toán 11 Tập 2
Luyện tập 3 trang 111 Toán 11 Tập 2
Cho hình chóp đều S.ABC. Gọi A’, B’, C’ lần lượt là trung điểm của các đoạn thẳng SA, SB, SC. Chứng minh rằng phần hình chóp đã cho giới hạn bởi hai mặt phẳng (ABC) và (A’B’C’) là hình chóp cụt đều. Luyện tập 3 trang 111 Toán 11 Tập 2

Hoạt động 4 trang 112 Toán 11 Tập 2
Hãy nêu lại công thức tính thể tích của khối lăng trụ đứng tam giác, khối lăng trụ đứng tứ giác. Hoạt động 4 trang 112 Toán 11 Tập 2
Luyện tập 4 trang 112 Toán 11 Tập 2
Tính thể tích của khối lăng trụ ABC.A’B’C’ biết tất cả các cạnh bằng a và hình chiếu của A’ trên mặt phẳng (ABC) là trung điểm của AB. Luyện tập 4 trang 112 Toán 11 Tập 2

Luyện tập 5 trang 114 Toán 11 Tập 2
Luyện tập 5 trang 114 Toán 11 Tập 2
Luyện tập 6 trang 114 Toán 11 Tập 2
Một thùng đựng rác có dạng khối chóp cụt tứ giác đều với hai cạnh đáy lần lượt dài 2 dm và 3 dm, chiều cao bằng 4 dm. Tính thể tích của thùng đựng rác. Luyện tập 6 trang 114 Toán 11 Tập 2
Giải bài tập Bài tập cuối chương 8
Bài 1 trang 116 Toán 11 Tập 2
Cho hình lập phương MNPQ.M’N’P’Q’ có cạnh bằng a. Bài 1 trang 116 Toán 11 Tập 2
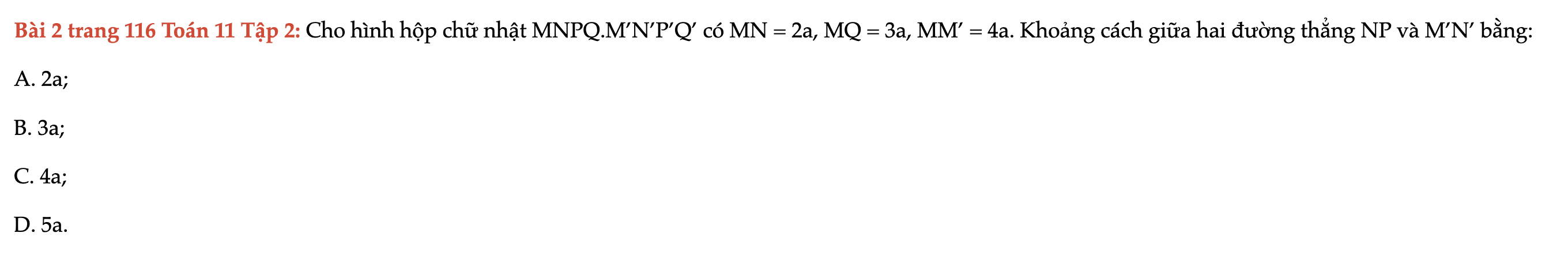
Bài 2 trang 116 Toán 11 Tập 2
Cho hình hộp chữ nhật MNPQ.M’N’P’Q’ có MN = 2a, MQ = 3a, MM’ = 4a. Khoảng cách giữa hai đường thẳng NP và M’N’ bằng. Bài 2 trang 116 Toán 11 Tập 2

Bài 3 trang 116 Toán 11 Tập 2
Cho khối lăng trụ có diện tích đáy bằng a2 và chiều cao bằng 3a. Thể tích của khối lăng trụ đó bằng. Bài 3 trang 116 Toán 11 Tập 2

Bài 4 trang 116 Toán 11 Tập 2
Cho khối chóp có diện tích đáy là a2 và chiều cao là 3a. Thể tích của khối chóp bằng. Bài 4 trang 116 Toán 11 Tập 2
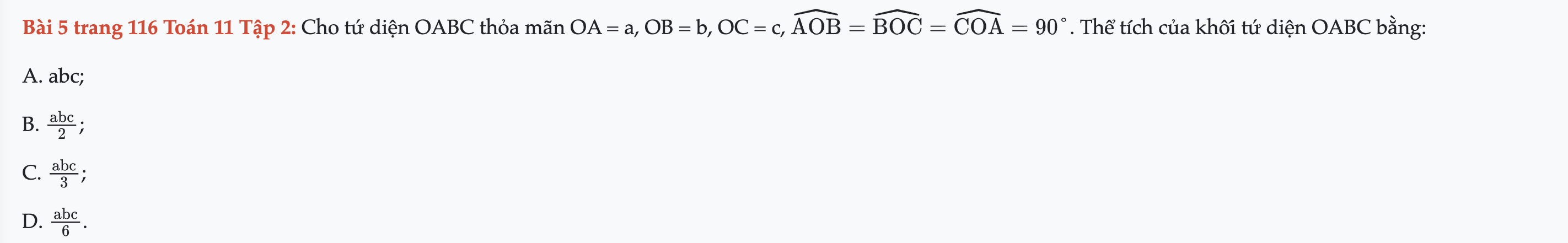
Bài 5 trang 116 Toán 11 Tập 2
Cho tứ diện OABC thỏa mãn OA = a, OB = b, OC = c, góc AOB = BOC = COA = 90°. Thể tích của khối tứ diện OABC bằng. Bài 5 trang 116 Toán 11 Tập 2

Bài 6 trang 116 Toán 11 Tập 2
Cho hình chóp S.ABC có SA ⊥ (ABC), AC ⊥ BC, SA = BC = a căn 3, AC = a (Hình 99). Bài 6 trang 116 Toán 11 Tập 2

Bài 7 trang 117 Toán 11 Tập 2
Cho hình lăng trụ tam giác đều ABC.A’B’C’ có tất cả các cạnh bằng a. Gọi M là trung điểm của AB (Hình 100). Tính góc giữa hai đường thẳng AB và B’C’. Bài 7 trang 117 Toán 11 Tập 2

Bài 8 trang 117 Toán 11 Tập 2
Đền Kukulcan (Hình 101) là một kim tự tháp Trung Mỹ nằm ở khu di tích Chichen Itza, Mexico, được người Maya xây vào khoảng từ thế kỉ IX đến thế kỉ XII. Bài 8 trang 117 Toán 11 Tập 2