Giải bài tập Toán 11 Chương 1: Hàm số lượng giác và phương trình lượng giác | Cánh Diều
Hướng dẫn giải Chương 1: Hàm số lượng giác và phương trình lượng giác
Giải bài tập Bài 1: Góc lượng giác. Giá trị lượng giác của góc lượng giác
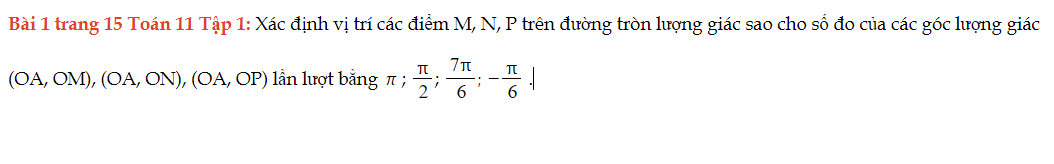
Bài 1 trang 15 Toán 11 Tập 1
Xác định vị trí các điểm M, N, P trên đường tròn lượng giác sao cho số đo của các góc lượng giác tương ứng thỏa yêu cầu. Bài 1 trang 15 Toán 11 Tập 1

Bài 2 trang 15 Toán 11 Tập 1
Cho góc yêu cầu tính giá trị lượng giác. Bài 2 trang 15 Toán 11 Tập 1.

Bài 3 trang 15 Toán 11 Tập 1
Cho góc yêu cầu tính giá trị lượng giác. Bài 3 trang 15 Toán 11 Tập 1

Bài 4 trang 15 Toán 11 Tập 1
Cho góc yêu cầu tính giá trị lượng giác. Bài 4 trang 15 Toán 11 Tập 1

Bài 5 trang 15 Toán 11 Tập 1
Cho mối quan hệ của 2 góc lượng giác, tính giá trị biểu thức. Bài 5 trang 15 Toán 11 Tập 1

Bài 6 trang 15 Toán 11 Tập 1
Một vệ tinh được định vị tại vị trí A trong không gian. Từ vị trí A, vệ tinh bắt đầu chuyển động quanh Trái Đất theo quỹ đạo là đường tròn với tâm là tâm O của Trái Đất, bán kính 9 000 km. Biết rằng vệ tinh chuyển động hết một vòng của quỹ đạo trong 2 giờ

Câu hỏi khởi động trang 5 Toán 11 Tập 1
Trên mặt chiếc đồng hồ, kim giây đang ở vị trí ban đầu chỉ vào số 3 (Hình 1). Kim giây quay ba vòng và một phần tư vòng đến vị trí cuối chỉ vào số 6. Câu hỏi khởi động trang 5 Toán 11 Tập 1
Hoạt động 1 trang 5 Toán 11 Tập 1
Nêu định nghĩa góc trong hình học phẳng. Hoạt động 1 trang 5 Toán 11 Tập 1

Luyện tập 1 trang 6 Toán 11 Tập 1
Hãy hoàn thành bảng chuyển đổi số đo độ và số đo radian của một số góc sau. Luyện tập 1 trang 6 Toán 11 Tập 1

Hoạt động 2 trang 6 Toán 11 Tập 1
So sánh chiều quay của kim đồng hồ với chiều quay từ tia Om đến tia Ox trong Hình 3a. Hoạt động 2 trang 6 Toán 11 Tập 1

Luyện tập 2 trang 7 Toán 11 Tập 1
Đọc tên góc lượng giác,tia đầu và tia cuối của góc lượng giác đó trong Hình 4b. Luyện tập 2 trang 7 Toán 11 Tập 1
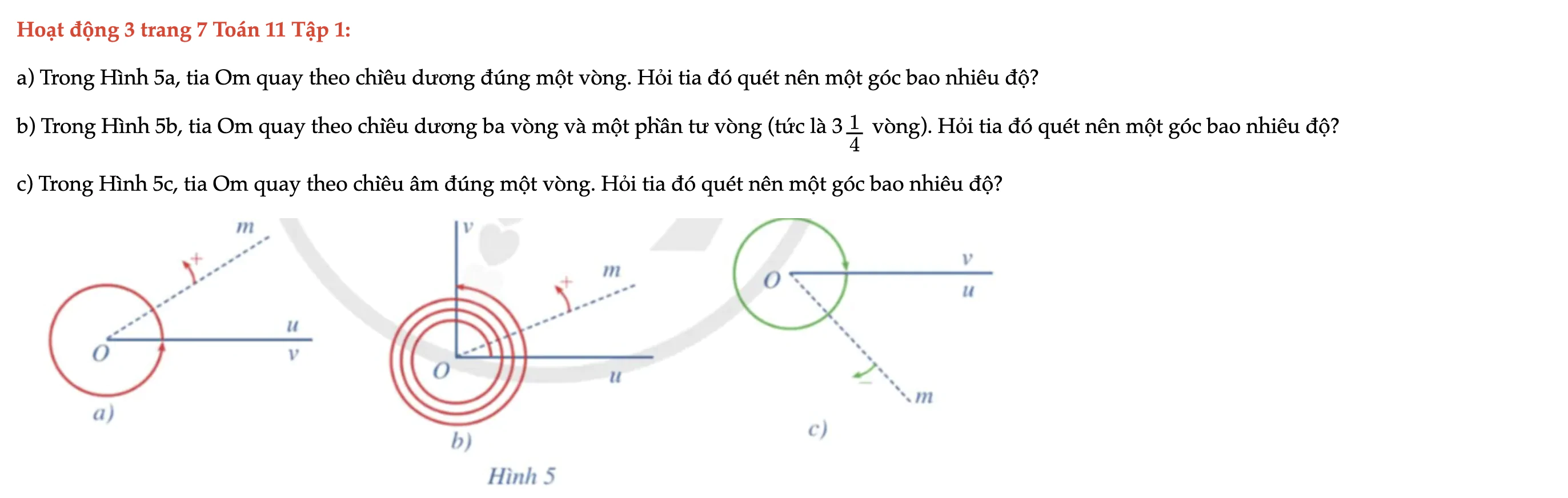
Hoạt động 3 trang 7 Toán 11 Tập 1
Trong Hình 5a, tia Om quay theo chiều dương đúng một vòng. Hỏi tia đó quét nên một góc bao nhiêu độ? Hoạt động 3 trang 7 Toán 11 Tập 1
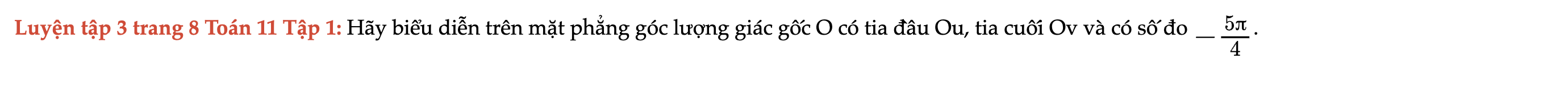
Luyện tập 3 trang 8 Toán 11 Tập 1
Hãy biểu diễn trên mặt phẳng góc lượng giác gốc O có tia đầu Ou, tia cuối Ov và có số đo -5π/4. Luyện tập 3 trang 8 Toán 11 Tập 1

Hoạt động 4 trang 8 Toán 11 Tập 1
Trong Hình 7a, ba góc lượng giác có cùng tia đầu Ou và tia cuối Ov, trong đó Ou ⊥ Ov. Xác định số đo của góc lượng giác trong các Hình 7b, 7c, 7d. Hoạt động 4 trang 8 Toán 11 Tập 1

Luyện tập 4 trang 9 Toán 11 Tập 1
Viết công thức biểu thị số đo của các góc lượng giác có cùng tia đầu, tia cuối với góc lượng giác có số đo bằng -4π/3. Luyện tập 4 trang 9 Toán 11 Tập 1

Hoạt động 5 trang 9 Toán 11 Tập 1
Cho góc (hình học) xOz, tia Oy nằm trong góc xOz (Hình 8). Nêu mối liên hệ giữa số đo của góc xOz và tổng số đo của hai góc xOy và yOz. Hoạt động 5 trang 9 Toán 11 Tập 1
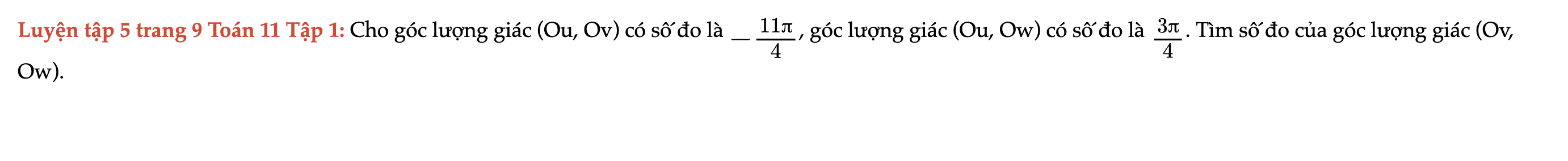
Luyện tập 5 trang 9 Toán 11 Tập 1
Cho góc lượng giác (Ou, Ov) có số đo là -11π/4, góc lượng giác (Ou, Ow) có số đo là 3π/4. Tìm số đo của góc lượng giác (Ov, Ow). Luyện tập 5 trang 9 Toán 11 Tập 1

Hoạt động 6 trang 10 Toán 11 Tập 1
Trong mặt phẳng toạ độ (định hướng) Oxy, hãy vẽ đường tròn tâm O với bán kính bằng 1. Hoạt động 6 trang 10 Toán 11 Tập 1

Luyện tập 6 trang 10 Toán 11 Tập 1
Xác định điểm N trên đường tròn lượng giác sao cho (OA, ON) = -π/3. Luyện tập 6 trang 10 Toán 11 Tập 1

Hoạt động 7 trang 10 Toán 11 Tập 1
Xác định điểm M trên đường tròn lượng giác sao cho (OA, OM) = 60°. Hoạt động 7 trang 10 Toán 11 Tập 1
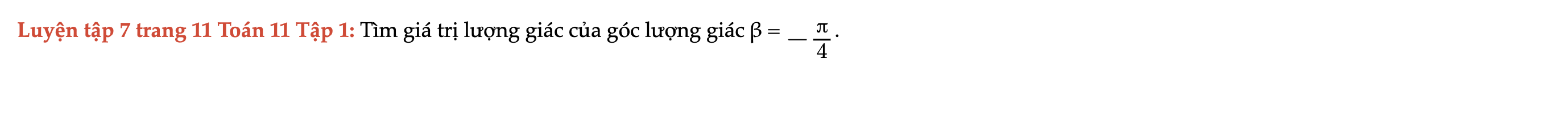
Luyện tập 7 trang 11 Toán 11 Tập 1
Tìm giá trị lượng giác của góc lượng giác β = -π/4. Luyện tập 7 trang 11 Toán 11 Tập 1
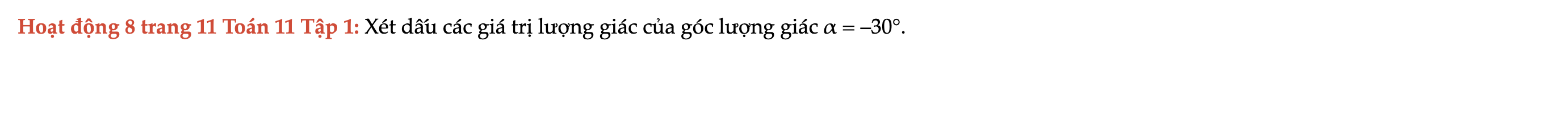
Hoạt động 8 trang 11 Toán 11 Tập 1
Xét dấu các giá trị lượng giác của góc lượng giác α = ‒30°. Hoạt động 8 trang 11 Toán 11 Tập 1
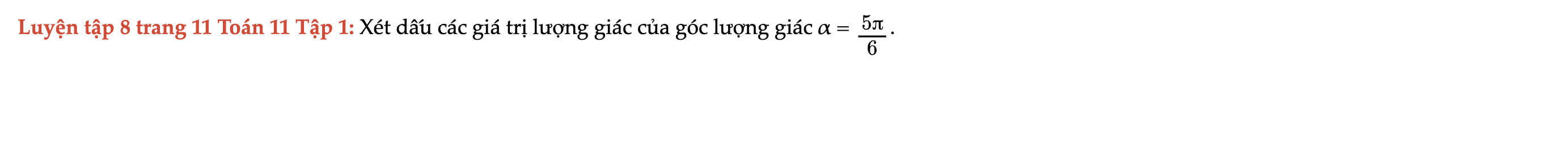
Luyện tập 8 trang 11 Toán 11 Tập 1
Xét dấu các giá trị lượng giác của góc lượng giác α = 5π/6. Luyện tập 8 trang 11 Toán 11 Tập 1
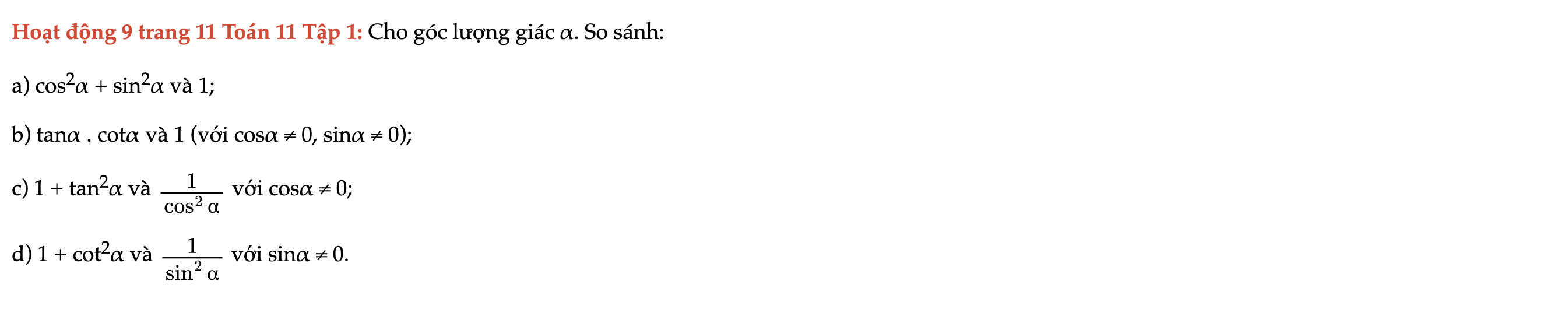
Hoạt động 9 trang 11 Toán 11 Tập 1
Cho góc lượng giác α. So sánh các đẳng thức sau. Hoạt động 9 trang 11 Toán 11 Tập 1
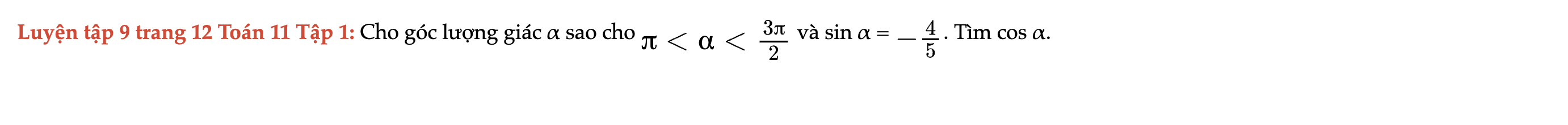
Luyện tập 9 trang 12 Toán 11 Tập 1
Cho góc lượng giác α sao cho π < α < 3π/2 và sin α = -4/5. Tìm cos α. Luyện tập 9 trang 12 Toán 11 Tập 1
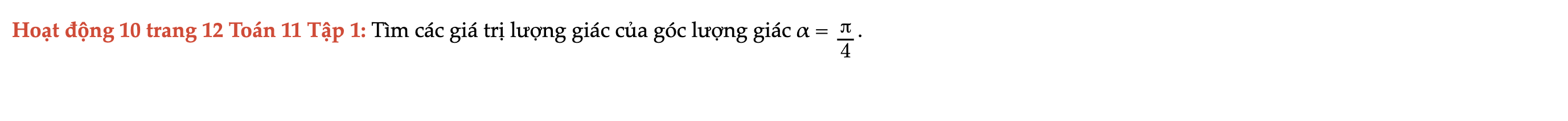
Hoạt động 10 trang 12 Toán 11 Tập 1
Tìm các giá trị lượng giác của góc lượng giác α = π/4. Hoạt động 10 trang 12 Toán 11 Tập 1
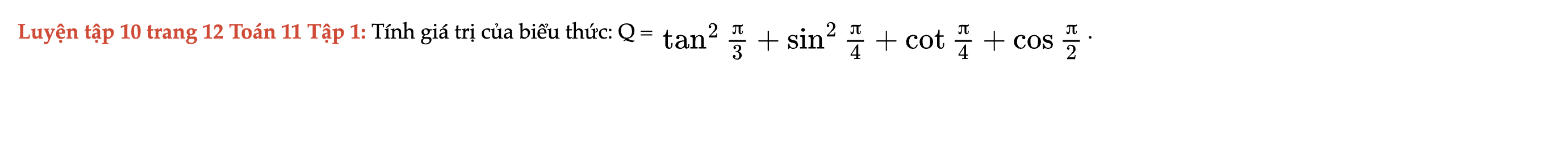
Luyện tập 10 trang 12 Toán 11 Tập 1
Tính giá trị của biểu thức sau. Luyện tập 10 trang 12 Toán 11 Tập 1

Hoạt động 11 trang 13 Toán 11 Tập 1
Trên đường tròn lượng giác, cho hai điểm M, M’ sao cho góc lượng giác (OA, OM) = α, góc lượng giác (OA, OM’) = – α (Hình 13). Hoạt động 11 trang 13 Toán 11 Tập 1

Luyện tập 11 trang 14 Toán 11 Tập 1
Luyện tập 11 trang 14 Toán 11 Tập 1
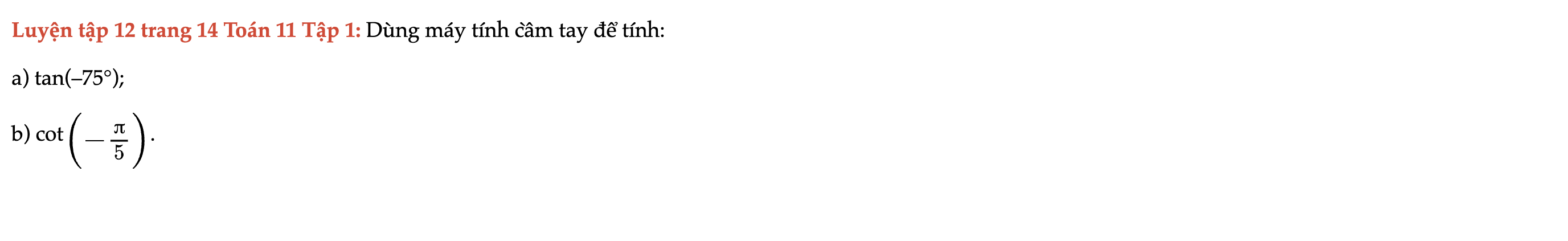
Luyện tập 12 trang 14 Toán 11 Tập 1
Dùng máy tính cầm tay để tính các câu sau. Luyện tập 12 trang 14 Toán 11 Tập 1
Giải bài tập Bài 2: Các phép biến đổi lượng giác
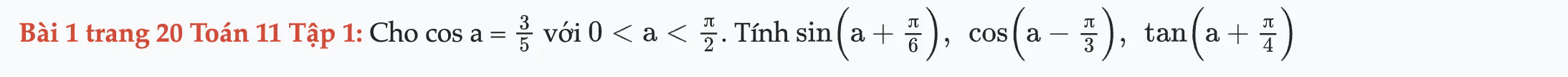
Bài 1 trang 20 Toán 11 Tập 1
Bài 1 trang 20 Toán 11 Tập 1

Bài 2 trang 20 Toán 11 Tập 1
Tính. Bài 2 trang 20 Toán 11 Tập 1
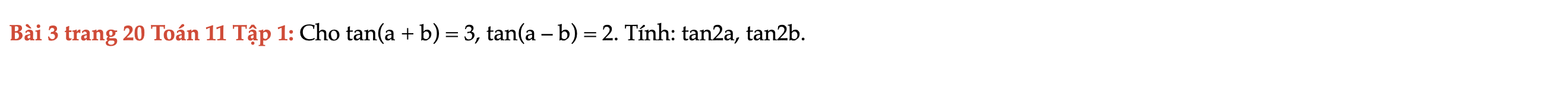
Bài 3 trang 20 Toán 11 Tập 1
Cho tan(a + b) = 3, tan(a – b) = 2. Tính: tan2a, tan2b. Bài 3 trang 20 Toán 11 Tập 1

Bài 4 trang 20 Toán 11 Tập 1
Tính cos2a, cos4a. Bài 4 trang 20 Toán 11 Tập 1

Bài 5 trang 20 Toán 11 Tập 1
Cho sina + cosa = 1. Tính sin2a. Bài 5 trang 20 Toán 11 Tập 1

Bài 6 trang 21 Toán 11 Tập 1
Bài 6 trang 21 Toán 11 Tập 1
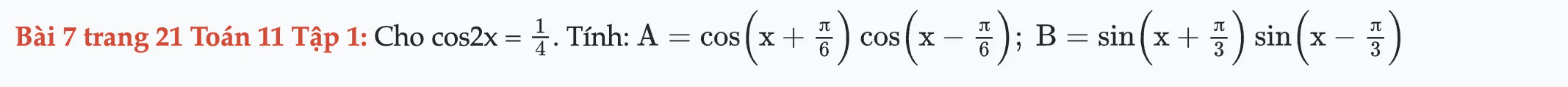
Bài 7 trang 21 Toán 11 Tập 1
Bài 7 trang 21 Toán 11 Tập 1
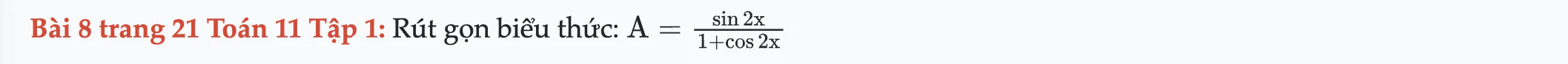
Bài 8 trang 21 Toán 11 Tập 1
Rút gọn biểu thức A. Bài 8 trang 21 Toán 11 Tập 1

Bài 9 trang 21 Toán 11 Tập 1
Một sợi cáp R được gắn vào một cột thẳng đứng ở vị trí cách mặt đất 14 m. Một sợi cáp S khác cũng được gắn vào cột đó ở vị trí cách mặt đất 12 m. Bài 9 trang 21 Toán 11 Tập 1

Bài 10 trang 21 Toán 11 Tập 1
Có hai chung cư cao tầng I và II xây cạnh nhau với khoảng cách giữa chúng là HK = 20 m. Để đảm bảo an ninh, trên nóc chung cư II người ta lắp camera ở vị trí C. Bài 10 trang 21 Toán 11 Tập 1

Câu hỏi khởi động trang 16 Toán 11 Tập 1
Ở lớp dưới, ta đã làm quen với một số phép tính trong tập hợp các số thực, chẳng hạn: phép tính luỹ thừa với số mũ tự nhiên và những công thức để tính toán hay biến đổi những biểu thức chứa các luỹ thừa như vậy. Câu hỏi khởi động trang 16 Toán 11 Tập 1

Hoạt động 1 trang 16 Toán 11 Tập 1
Cho a = π/6; b = π/3. Hãy tính sina, cosa, sinb, cosb và sin(a + b). Từ đó rút ra đẳng thức sin(a + b) = sina cosb + cosa sinb (*). Hoạt động 1 trang 16 Toán 11 Tập 1

Luyện tập 1 trang 16 Toán 11 Tập 1
Luyện tập 1 trang 16 Toán 11 Tập 1

Hoạt động 2 trang 17 Toán 11 Tập 1
Tính cos(a + b) bằng cách biến đổi cos(a + b) = sin(π/2 - (a + b)) = sin((π/2 - a) - b) và sử dụng công thức cộng đối với sin. Hoạt động 2 trang 17 Toán 11 Tập 1

Luyện tập 2 trang 17 Toán 11 Tập 1
Tính cos15°. Luyện tập 2 trang 17 Toán 11 Tập 1

Hoạt động 3 trang 17 Toán 11 Tập 1
Sử dụng công thức cộng đối với sin và côsin, hãy tính tan(a + b) theo tana và tanb khi các biểu thức đều có nghĩa. Hoạt động 3 trang 17 Toán 11 Tập 1

Luyện tập 3 trang 17 Toán 11 Tập 1
Tính tan165°. Luyện tập 3 trang 17 Toán 11 Tập 1
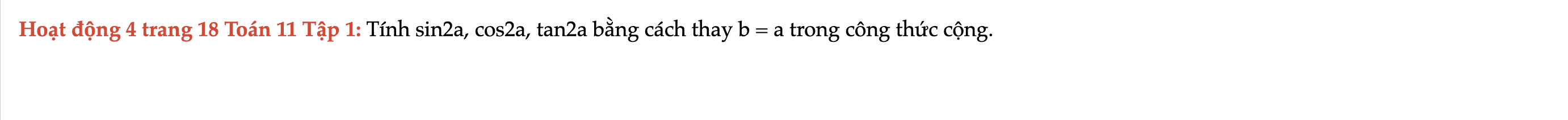
Hoạt động 4 trang 18 Toán 11 Tập 1
Tính sin2a, cos2a, tan2a bằng cách thay b = a trong công thức cộng. Hoạt động 4 trang 18 Toán 11 Tập 1

Luyện tập 4 trang 18 Toán 11 Tập 1
Cho tana/2 = -2. Tính tana. Luyện tập 4 trang 18 Toán 11 Tập 1

Luyện tập 5 trang 18 Toán 11 Tập 1
Tính: sinπ/8; cosπ/8. Luyện tập 5 trang 18 Toán 11 Tập 1

Hoạt động 5 trang 18 Toán 11 Tập 1
Sử dụng công thức cộng, rút gọn mỗi biểu thức sau. Hoạt động 5 trang 18 Toán 11 Tập 1
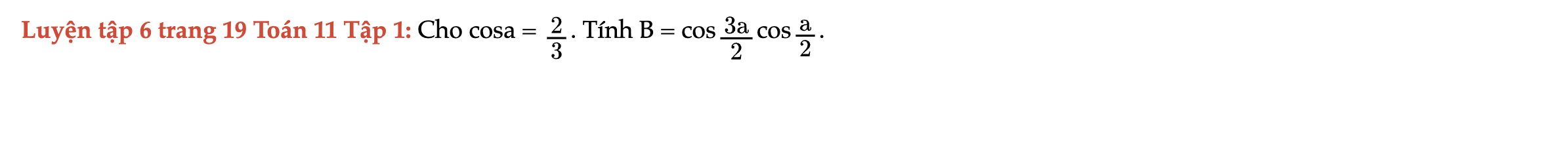
Luyện tập 6 trang 19 Toán 11 Tập 1
Luyện tập 6 trang 19 Toán 11 Tập 1

Hoạt động 6 trang 19 Toán 11 Tập 1
Sử dụng công thức biến đổi tích thành tổng và đặt a + b = u; a − b = v rồi biến đổi các biểu thức sau thành tích: cosu + cosv; cosu – cos v; sinu + sinv; sinu – sinv. Hoạt động 6 trang 19 Toán 11 Tập 1

Luyện tập 7 trang 19 Toán 11 Tập 1
Tính biểu thức sau. Luyện tập 7 trang 19 Toán 11 Tập 1
Giải bài tập Bài 3: Hàm số lượng giác và đồ thị

Bài 1 trang 31 Toán 11 Tập 1
Dùng đồ thị hàm số, tìm giá trị của x trên đoạn [‒2π; 2π] để hàm số y = sinx nhận giá trị bằng 1. Bài 1 trang 31 Toán 11 Tập 1

Bài 2 trang 31 Toán 11 Tập 1
Dùng đồ thị hàm số, tìm giá trị của x trên khoảng (-π; 3π/2) để hàm số y = tanx nhận giá trị bằng ‒1. Bài 2 trang 31 Toán 11 Tập 1

Bài 3 trang 31 Toán 11 Tập 1
Xét sự biến thiên của mỗi hàm số sau trên các khoảng tương ứng. Bài 3 trang 31 Toán 11 Tập 1

Bài 4 trang 31 Toán 11 Tập 1
Dùng đồ thị hàm số, hãy cho biết Với mỗi m ∈ [‒1;1], có bao nhiêu giá trị α ∈ (-π/2; π/2) sao cho sinα = m. Bài 4 trang 31 Toán 11 Tập 1

Bài 5 trang 31 Toán 11 Tập 1
Xét tính chẵn, lẻ của các hàm số. Bài 5 trang 31 Toán 11 Tập 1

Bài 6 trang 31 Toán 11 Tập 1
Một dao động điều hoà có phương trình li độ dao động là: x = Acos(ωt + φ), trong đó A, φ, ω là các hằng số (ω > 0). Khi đó, chu kì T của dao động là T = 2π/ω. Bài 6 trang 31 Toán 11 Tập 1

Bài 7 trang 31 Toán 11 Tập 1
Trong bài toán mở đầu, hãy chỉ ra một số giá trị của x để ống đựng nước cách mặt nước 2m. Bài 7 trang 31 Toán 11 Tập 1

Hoạt động 1 trang 22 Toán 11 Tập 1
Cho hàm số f(x) = x^2. Với x ∈ ℝ, hãy so sánh f(‒x) và f(x). Quan sát parabol (P) là đồ thị của hàm số f(x) = x^2 (Hình 19) và cho biết trục đối xứng của (P) là đường thẳng nào. Hoạt động 1 trang 22 Toán 11 Tập 1

Luyện tập 1 trang 23 Toán 11 Tập 1
Chứng tỏ rằng hàm số g(x) = x^3 là hàm số lẻ. Luyện tập 1 trang 23 Toán 11 Tập 1
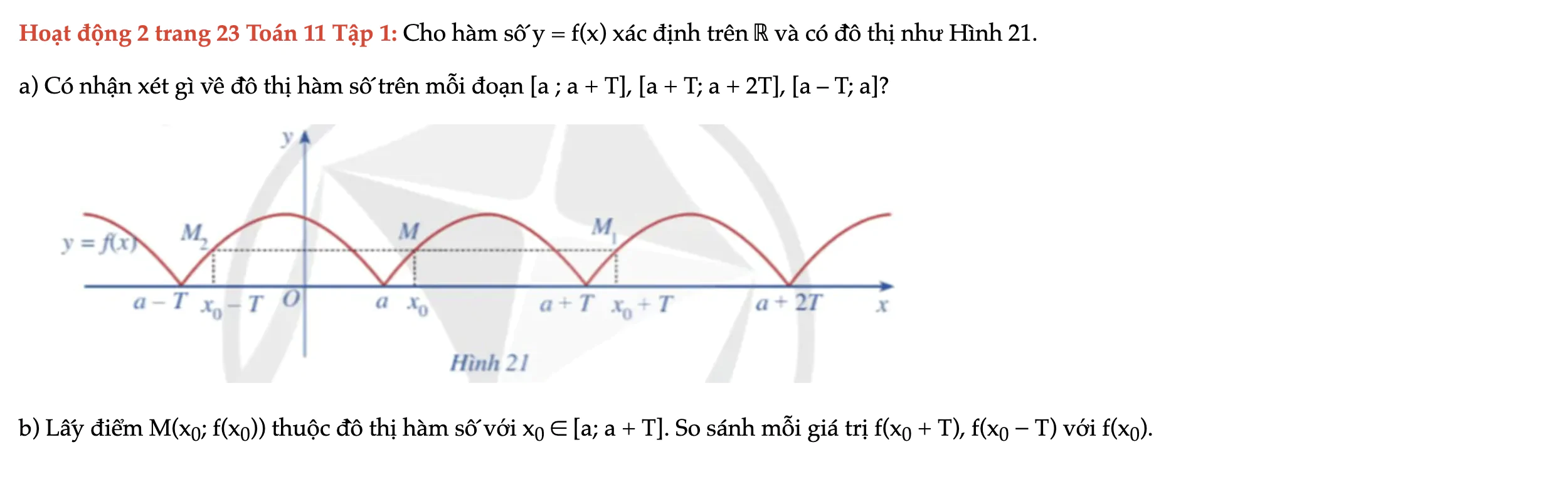
Hoạt động 2 trang 23 Toán 11 Tập 1
Cho hàm số y = f(x) xác định trên ℝ và có đồ thị như Hình 21. Có nhận xét gì về đồ thị hàm số trên mỗi đoạn [a ; a + T], [a + T; a + 2T], [a – T; a]? Hoạt động 2 trang 23 Toán 11 Tập 1

Luyện tập 2 trang 23 Toán 11 Tập 1
Cho ví dụ về hàm số tuần hoàn. Luyện tập 2 trang 23 Toán 11 Tập 1

Hoạt động 3 trang 24 Toán 11 Tập 1
Với mỗi số thực x, tồn tại duy nhất điểm M trên đường tròn lượng giác sao cho (OA, OM) = x (rad) (Hình 22). Hãy xác định sinx. Hoạt động 3 trang 24 Toán 11 Tập 1

Hoạt động 4 trang 24 Toán 11 Tập 1
Cho hàm số y = sinx. Tìm giá trị y tương ứng với giá trị của x trong bảng sau. Hoạt động 4 trang 24 Toán 11 Tập 1
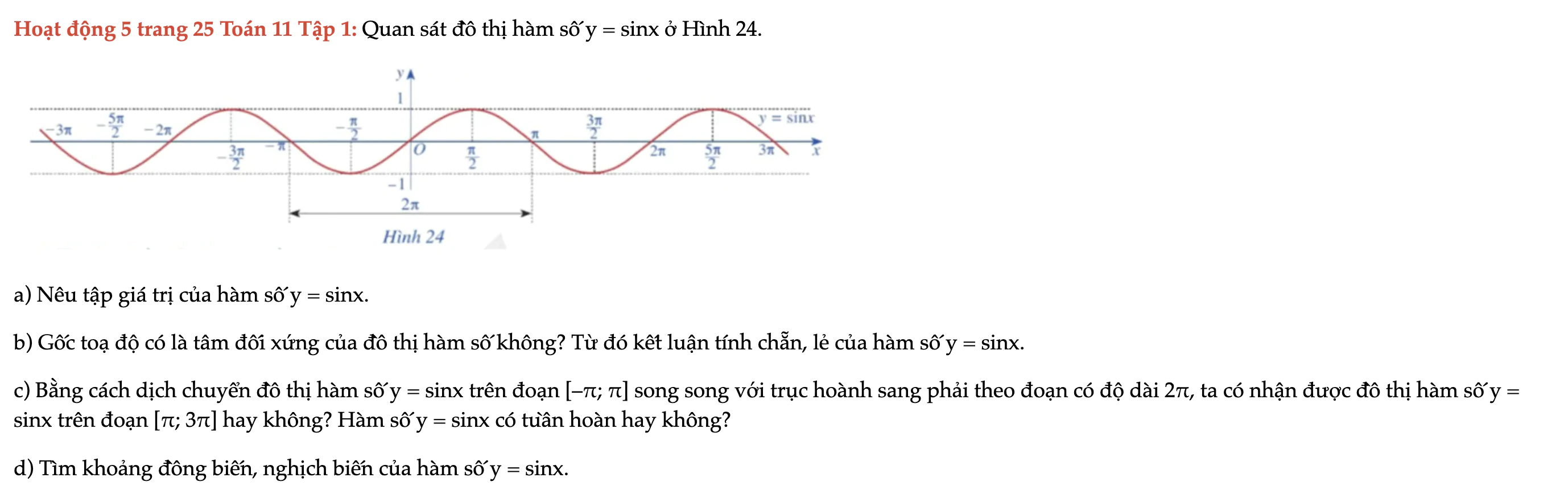
Hoạt động 5 trang 25 Toán 11 Tập 1
Quan sát đồ thị hàm số y = sinx ở Hình 24. Nêu tập giá trị của hàm số y = sinx. Gốc toạ độ có là tâm đối xứng của đồ thị hàm số không? Từ đó kết luận tính chẵn, lẻ của hàm số y = sinx. Hoạt động 5 trang 25 Toán 11 Tập 1

Luyện tập 3 trang 25 Toán 11 Tập 1
Hàm số y = sinx đồng biến hay nghịch biến trên khoảng (-7π/2; -5π/2). Luyện tập 3 trang 25 Toán 11 Tập 1

Hoạt động 6 trang 26 Toán 11 Tập 1
Với mỗi số thực x, tồn tại duy nhất điểm M trên đường tròn lượng giác sao cho (OA, OM) = x (rad) (Hình 25). Hãy xác định cosx. Hoạt động 6 trang 26 Toán 11 Tập 1

Hoạt động 7 trang 26 Toán 11 Tập 1
Cho hàm số y = cosx. Tìm giá trị y tương ứng với giá trị của x trong bảng sau. Hoạt động 7 trang 26 Toán 11 Tập 1

Hoạt động 8 trang 27 Toán 11 Tập 1
Quan sát đồ thị hàm số y = cosx ở Hình 27. Nêu tập giá trị của hàm số y = cosx. Trục tung có là trục đối xứng của đồ thị hàm số không? Từ đó kết luận tính chẵn, lẻ của hàm số y = cosx. Hoạt động 8 trang 27 Toán 11 Tập 1

Luyện tập 4 trang 27 Toán 11 Tập 1
Hàm số y = cosx đồng biến hay nghịch biến trên khoảng (‒2π; ‒π)? Luyện tập 4 trang 27 Toán 11 Tập 1
Hoạt động 9 trang 27 Toán 11 Tập 1
Với mỗi số thực x ∈ D, hãy nêu định nghĩa tanx. Hoạt động 9 trang 27 Toán 11 Tập 1

Hoạt động 10 trang 28 Toán 11 Tập 1
Cho hàm số y = tanx. Tìm giá trị y tương ứng với giá trị của x trong bảng sau. Hoạt động 10 trang 28 Toán 11 Tập 1

Hoạt động 11 trang 28 Toán 11 Tập 1
Quan sát đồ thị hàm số y = tanx ở Hình 29. Nêu tập giá trị của hàm số y = tanx. Gốc toạ độ có là tâm đối xứng của đồ thị hàm số không? Từ đó kết luận tính chẵn, lẻ của hàm số y = tanx. Hoạt động 11 trang 28 Toán 11 Tập 1
Luyện tập 5 trang 29 Toán 11 Tập 1
Với mỗi số thực m, tìm số giao điểm của đường thẳng y = m và đồ thị hàm số y = tanx trên khoảng (-π/2; π/2). Luyện tập 5 trang 29 Toán 11 Tập 1

Hoạt động 12 trang 29 Toán 11 Tập 1
Xét tập hợp E = ℝ \ {kπ | k ∈ ℤ}. Với mỗi số thực x ∈ E, hãy nêu định nghĩa cotx. Hoạt động 12 trang 29 Toán 11 Tập 1

Hoạt động 13 trang 29 Toán 11 Tập 1
Cho hàm số y = cotx. Tìm giá trị y tương ứng với giá trị của x trong bảng sau. Trong mặt phẳng toạ độ Oxy, hãy biểu diễn các điểm (x; y) trong bảng giá trị ở câu a. Hoạt động 13 trang 29 Toán 11 Tập 1

Hoạt động 14 trang 30 Toán 11 Tập 1
Quan sát đồ thị hàm số y = cotx ở Hình 31. Nêu tập giá trị của hàm số y = cotx. Gốc toạ độ có là tâm đối xứng của đồ thị hàm số không? Từ đó kết luận tính chẵn, lẻ của hàm số y = cotx. Hoạt động 14 trang 30 Toán 11 Tập 1
Luyện tập 6 trang 30 Toán 11 Tập 1
Với mỗi số thực m, tìm số giao điểm của đường thẳng y = m và đồ thị hàm số y = cotx trên khoảng (0; π). Luyện tập 6 trang 30 Toán 11 Tập 1
Giải bài tập Bài 4: Phương trình lượng giác cơ bản

Bài 1 trang 40 Toán 11 Tập 1
Giải phương trình. Bài 1 trang 40 Toán 11 Tập 1

Bài 2 trang 40 Toán 11 Tập 1
Giải phương trình. Bài 2 trang 40 Toán 11 Tập 1

Bài 3 trang 40 Toán 11 Tập 1
Dùng đồ thị hàm số y = sinx, y = cosx để xác định số nghiệm của phương trình. Bài 3 trang 40 Toán 11 Tập 1

Bài 4 trang 40 Toán 11 Tập 1
Số giờ có ánh sáng mặt trời của một thành phố A ở vĩ độ 40° Bắc trong ngày thứ t của một năm không nhuận. Thành phố A có đúng 12 giờ có ánh sáng mặt trời vào ngày nào trong năm. Bài 4 trang 40 Toán 11 Tập 1

Bài 5 trang 40 Toán 11 Tập 1
Hội Lim (tỉnh Bắc Ninh) được tổ chức vào mùa xuân thường có trò chơi đánh đu. Khi người chơi đu nhún đều, cây đu sẽ đưa người chơi đu dao động quanh vị trí cân bằng (Hình 38). Bài 5 trang 40 Toán 11 Tập 1

Câu hỏi khởi động trang 32 Toán 11 Tập 1
Một vệ tinh nhân tạo bay quanh Trái Đất theo một quỹ đạo là đường elip (Hình 32). Độ cao h (km) của vệ tinh so với bề mặt Trái Đất được xác định bởi công thức h. Câu hỏi khởi động trang 32 Toán 11 Tập 1

Hoạt động 1 trang 32 Toán 11 Tập 1
Cho hai phương trình (với cùng ẩn x). Tìm tập nghiệm S1 của phương trình (1) và tập nghiệm S2 của phương trình (2). Hoạt động 1 trang 32 Toán 11 Tập 1
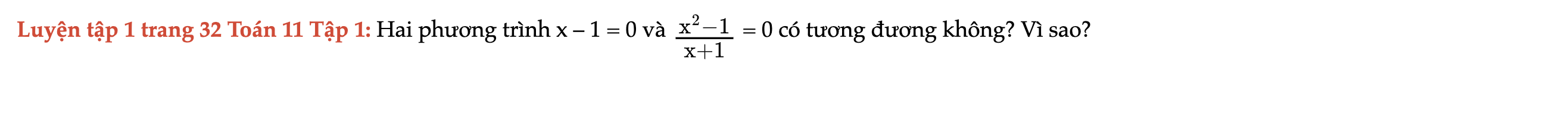
Luyện tập 1 trang 32 Toán 11 Tập 1
Hai phương trình sau có tương đương không? Vì sao? Luyện tập 1 trang 32 Toán 11 Tập 1

Hoạt động 2 trang 33 Toán 11 Tập 1
Khẳng định 3x ‒ 6 = 0 ⇔ 3x = 6 đúng hay sai? Hoạt động 2 trang 33 Toán 11 Tập 1
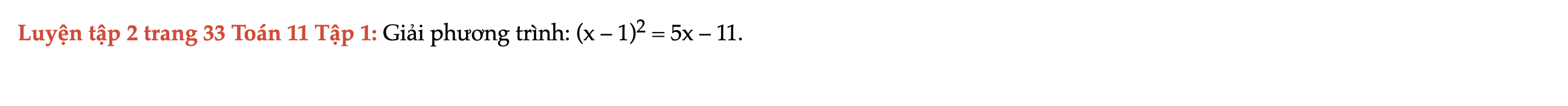
Luyện tập 2 trang 33 Toán 11 Tập 1
Giải phương trình: (x – 1)^2 = 5x – 11. Luyện tập 2 trang 33 Toán 11 Tập 1

Hoạt động 3 trang 33 Toán 11 Tập 1
Đường thẳng d: y = 1/2 cắt đồ thị hàm số y = sinx, x ∈ [‒π; π] tại hai giao điểm A0, B0 (Hình 33). Tìm hoành độ của hai giao điểm A0, B0. Hoạt động 3 trang 33 Toán 11 Tập 1

Luyện tập 3 trang 34 Toán 11 Tập 1
Giải phương trình: sin x = căn 3/2. Luyện tập 3 trang 34 Toán 11 Tập 1
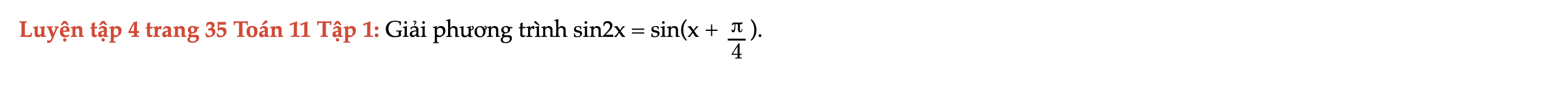
Luyện tập 4 trang 35 Toán 11 Tập 1
Giải phương trình sin2x = sin(x + π/4). Luyện tập 4 trang 35 Toán 11 Tập 1

Hoạt động 4 trang 35 Toán 11 Tập 1
Đường thẳng d: y = 1/2 cắt đồ thị hàm số y = cosx, x ∈ [‒π; π] tại hai giao điểm C0, D0 (Hình 34). Tìm hoành độ của hai giao điểm C0, D0. Hoạt động 4 trang 35 Toán 11 Tập 1

Luyện tập 5 trang 36 Toán 11 Tập 1
Giải phương trình: cosx = -1/2. Tìm góc lượng giác x sao cho cosx = cos(‒87°). Luyện tập 5 trang 36 Toán 11 Tập 1

Luyện tập 6 trang 37 Toán 11 Tập 1
Giải phương trình được nêu trong bài toán mở đầu. Luyện tập 6 trang 37 Toán 11 Tập 1
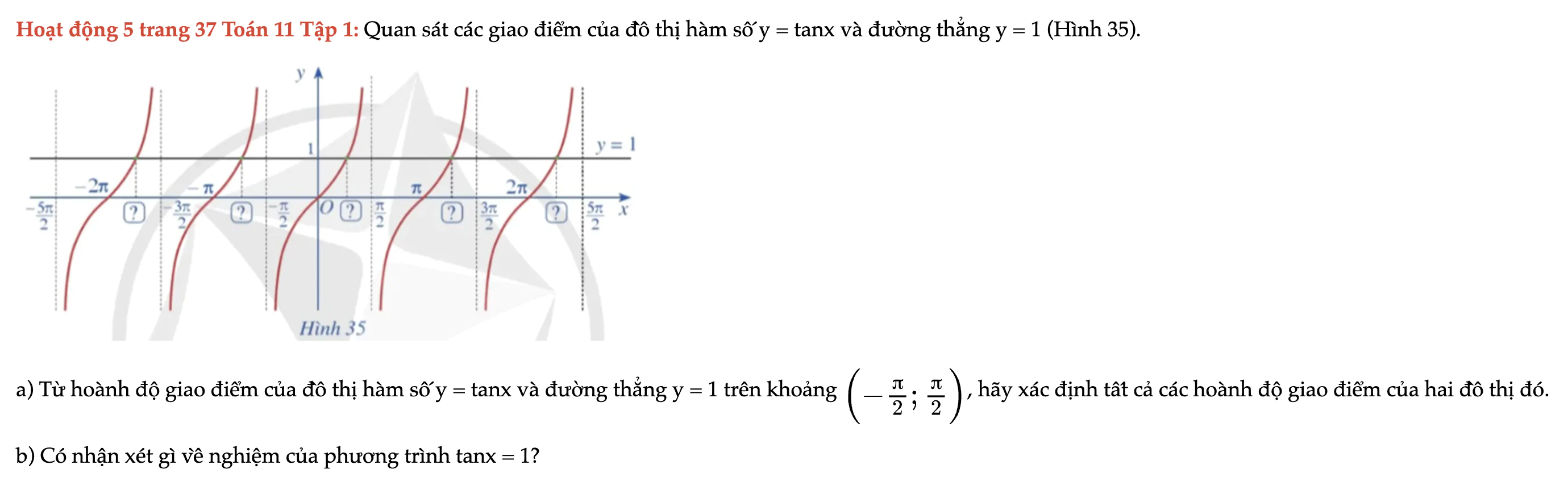
Hoạt động 5 trang 37 Toán 11 Tập 1
Quan sát các giao điểm của đồ thị hàm số y = tanx và đường thẳng y = 1 (Hình 35). Hoạt động 5 trang 37 Toán 11 Tập 1

Luyện tập 7 trang 37 Toán 11 Tập 1
Giải phương trình: tanx = 0. Tìm góc lượng giác x sao cho tanx = tan67°. Luyện tập 7 trang 37 Toán 11 Tập 1

Hoạt động 6 trang 38 Toán 11 Tập 1
Quan sát các giao điểm của đồ thị hàm số y = cotx và đường thẳng y = ‒1 (Hình 36). Hoạt động 6 trang 38 Toán 11 Tập 1

Luyện tập 8 trang 39 Toán 11 Tập 1
Giải phương trình: cotx = 1. Tìm góc lượng giác x sao cho cotx = cot(‒83°). Luyện tập 8 trang 39 Toán 11 Tập 1

Luyện tập 9 trang 39 Toán 11 Tập 1
Sử dụng MTCT để giải mỗi phương trình sau với kết quả là radian (làm tròn kết quả đến hàng phần nghìn). Luyện tập 9 trang 39 Toán 11 Tập 1
Giải bài tập Bài tập cuối chương 1

Bài 1 trang 41 Toán 11 Tập 1
Hàm số y = sinx đồng biến trên khoảng. Bài 1 trang 41 Toán 11 Tập 1

Bài 2 trang 41 Toán 11 Tập 1
Hàm số nghịch biến trên khoảng (π; 2π) là. Bài 2 trang 41 Toán 11 Tập 1
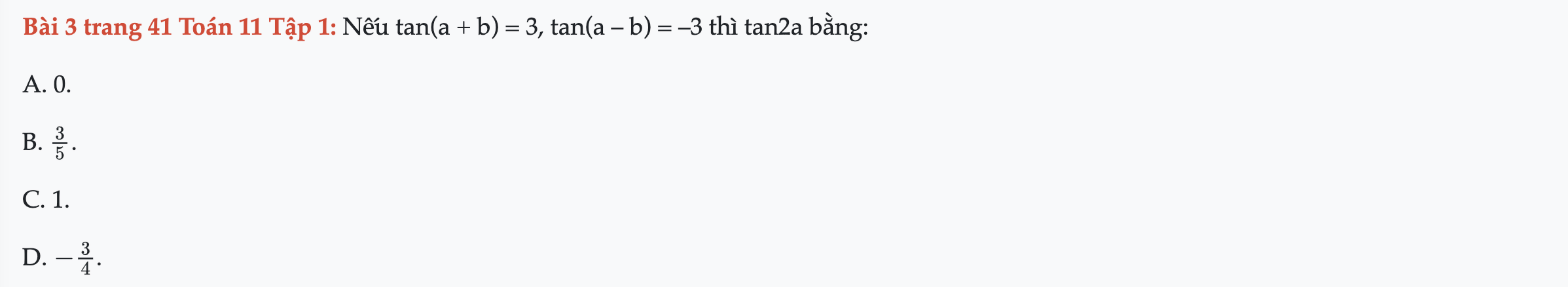
Bài 3 trang 41 Toán 11 Tập 1
Nếu tan(a + b) = 3, tan(a – b) = ‒3 thì tan2a bằng. Bài 3 trang 41 Toán 11 Tập 1

Bài 4 trang 41 Toán 11 Tập 1
Nếu cosa = 1/4 thì cos2a bằng. Bài 4 trang 41 Toán 11 Tập 1
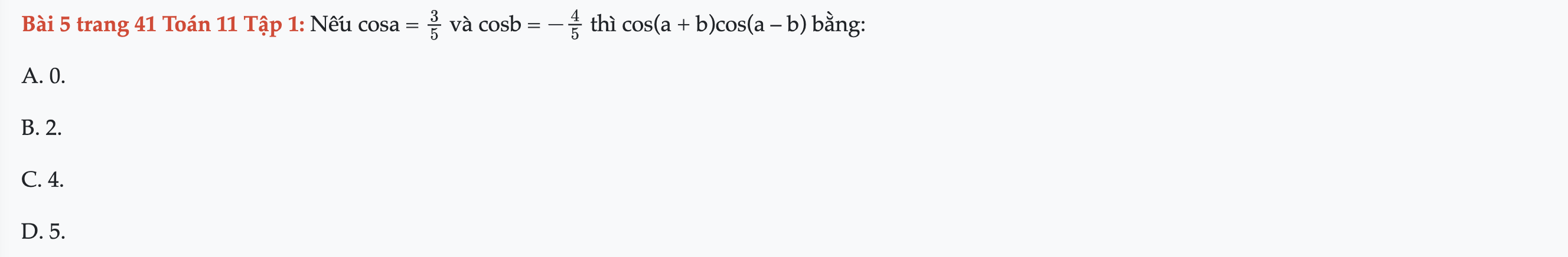
Bài 5 trang 41 Toán 11 Tập 1
Nếu cosa = 3/5 và cosb = -4/5 thì cos(a + b)cos(a – b) bằng. Bài 5 trang 41 Toán 11 Tập 1
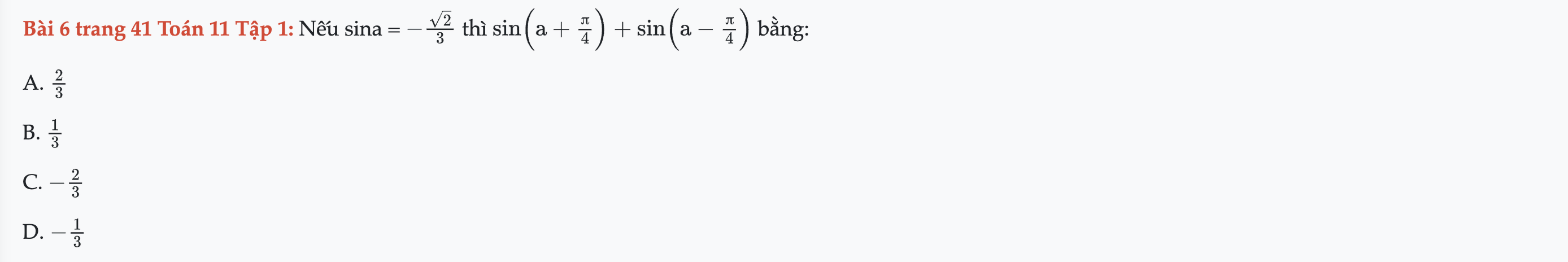
Bài 6 trang 41 Toán 11 Tập 1
Bài 6 trang 41 Toán 11 Tập 1

Bài 7 trang 41 Toán 11 Tập 1
Số nghiệm của phương trình cosx = 0 trên đoạn [0; 10π] là. Bài 7 trang 41 Toán 11 Tập 1

Bài 8 trang 41 Toán 11 Tập 1
Số nghiệm của phương trình sinx = 0 trên đoạn [0; 10π] là. Bài 8 trang 41 Toán 11 Tập 1

Bài 9 trang 41 Toán 11 Tập 1
Nghiệm của phương trình cotx = ‒1 là. Bài 9 trang 41 Toán 11 Tập 1
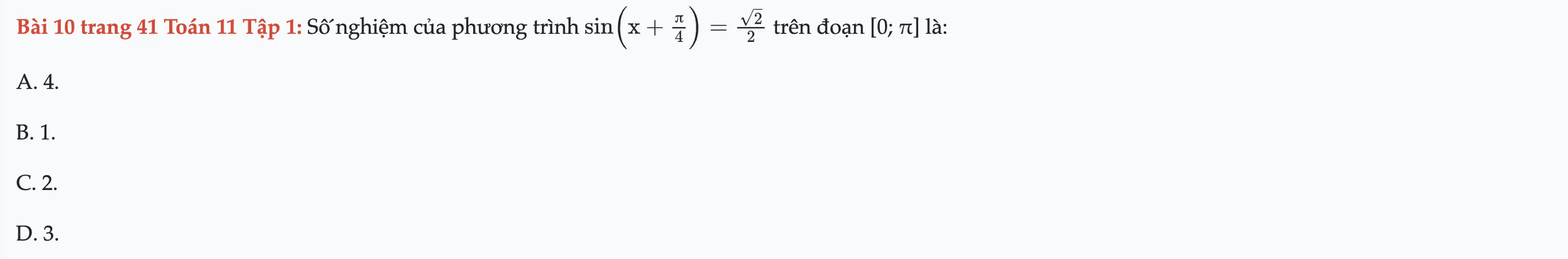
Bài 10 trang 41 Toán 11 Tập 1
Số nghiệm của phương trình đã cho trên đoạn [0; π] l. Bài 10 trang 41 Toán 11 Tập 1
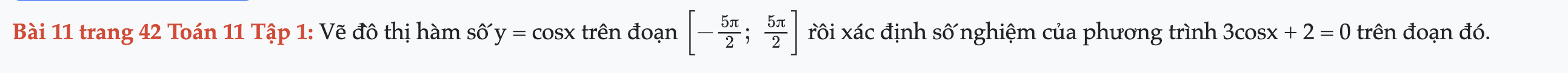
Bài 11 trang 42 Toán 11 Tập 1
Vẽ đồ thị hàm số y = cosx trên đoạn [-5π/2; 5π/2] rồi xác định số nghiệm của phương trình 3cosx + 2 = 0 trên đoạn đó. Bài 11 trang 42 Toán 11 Tập 1

Bài 12 trang 42 Toán 11 Tập 1
Giải các phương trình sau. Bài 12 trang 42 Toán 11 Tập 1

Bài 13 trang 42 Toán 11 Tập 1
Hằng ngày, mực nước của một con kênh lên xuống theo thuỷ triều. Độ sâu h(m) của mực nước trong kênh tính theo thời gian t (giờ) trong một ngày (0 ≤ t < 24). Tìm t để độ sâu của mực nước là. Bài 13 trang 42 Toán 11 Tập 1

Bài 14 trang 42 Toán 11 Tập 1
Một cây cầu có dạng cung OA của đồ thị hàm số y = 4,8sin(x/9) và được mô tả trong hệ trục toạ độ với đơn vị trục là mét như ở Hình 39. Bài 14 trang 42 Toán 11 Tập 1