Giải bài tập Bài 4 trang 15 Toán 11 Tập 1 | Toán 11 - Cánh diều
Hướng dẫn giải chi tiết từng bước bài tập Bài 4 trang 15 Toán 11 Tập 1. Bài 1: Góc lượng giác. Giá trị lượng giác của góc lượng giác. Toán 11 - Cánh diều
Đề bài:
Tính các giá trị lượng giác của góc α trong mỗi trường hợp sau:
a) 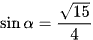 với
với 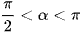 ;
;
b) 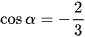 với ‒π < α < 0;
với ‒π < α < 0;
c) tanα = 3 với ‒π < α < 0;
d) cotα = ‒2 với 0 < α < π.
Đáp án và cách giải chi tiết:
a) Do 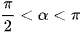 nên cosα < 0.
nên cosα < 0.
Áp dụng công thức sin2α + cos2α = 1, ta có:
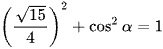
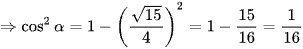
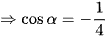 (do cosα < 0).
(do cosα < 0).
Ta có: 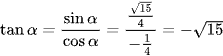
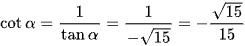
Vậy 
b) Do ‒π < α < 0 nên sinα < 0.
Áp dụng công thức sin2α + cos2α = 1, ta có:

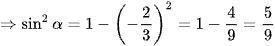
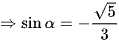 (do sinα < 0).
(do sinα < 0).
Ta có: 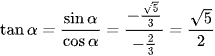 ;
;
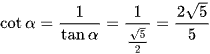
Vậy 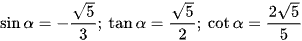
c) Do ‒π < α < 0 nên sinα < 0 và cosα > 0 khi khi 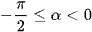 , cosα < 0 khi
, cosα < 0 khi 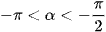
Mà tanα = 3 > 0, do đó 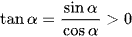 , từ đó suy ra cosα < 0.
, từ đó suy ra cosα < 0.
Áp dụng công thức tanα.cotα = 1, ta có 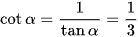
Áp dụng công thức 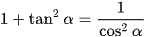 , ta có:
, ta có:
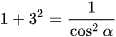 hay
hay 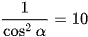
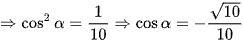 (do cosα < 0).
(do cosα < 0).
Áp dụng công thức 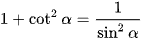 , ta có:
, ta có:
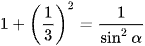 hay
hay 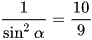
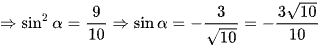 (do sinα < 0).
(do sinα < 0).
Vậy 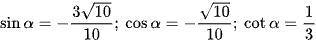
d) cotα = ‒2 với 0 < α < π.
Áp dụng công thức tanα.cotα = 1, ta có 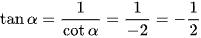
Do 0 < α < π nên sinα > 0.
Mà cotα = ‒2 < 0 nên 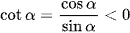 , suy ra cosα < 0.
, suy ra cosα < 0.
Áp dụng công thức 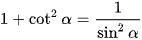 , ta có:
, ta có:
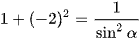 hay
hay 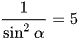
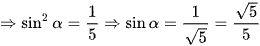 (do sinα > 0).
(do sinα > 0).
Ta có: 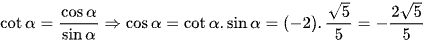
Nguồn: loigiaitoan.com
Tổng số đánh giá:
Xếp hạng: / 5 sao
Bài tập liên quan:
Bài 1 trang 15 Toán 11 Tập 1
Xác định vị trí các điểm M, N, P trên đường tròn lượng giác sao cho số đo của các góc lượng giác
(OA, OM), (OA, ON), (OA, OP) lần lượt bằng ; ; ; .
Bài 3 trang 15 Toán 11 Tập 1
Tính các giá trị lượng giác (nếu có) của mỗi góc sau:
a)
b)
c)
d) .
Bài 5 trang 15 Toán 11 Tập 1
Cho α + β = π. Tính:
a) A = sin2α + cos2β;
b) B = (sinα + cosβ)2 + (cosα + sinβ)2.
Bài 6 trang 15 Toán 11 Tập 1
Một vệ tinh được định vị tại vị trí A trong không gian. Từ vị trí A, vệ tinh bắt đầu chuyển động quanh Trái Đất theo quỹ đạo là đường tròn với tâm là tâm O của Trái Đất, bán kính 9 000 km. Biết rằng vệ tinh chuyển động hết một vòng của quỹ đạo trong 2 giờ.
a) Hãy tính quãng đường vệ tinh đã chuyển động được sau: 1 giờ; 3 giờ; 5 giờ.
b) Vệ tinh chuyển động được quãng đường 200 000 km sau bao nhiêu giờ (làm tròn kết quả đến hàng đơn vị)?
Câu hỏi khởi động trang 5 Toán 11 Tập 1
Trên mặt chiếc đồng hồ, kim giây đang ở vị trí ban đầu chỉ vào số 3 (Hình 1). Kim giây quay ba vòng và một phần tư vòng (tức là vòng) đến vị trí cuối chỉ vào số 6. Khi quay như thế, kim giây đã quét một góc với tia đầu chỉ vào số 3, tia cuối chỉ vào số 6.

Góc đó gợi nên khái niệm gì trong toán học? Những góc như thế có tính chất gì?
Luyện tập 1 trang 6 Toán 11 Tập 1
Hãy hoàn thành bảng chuyển đổi số đo độ và số đo radian của một số góc sau.

Hoạt động 2 trang 6 Toán 11 Tập 1
So sánh chiều quay của kim đồng hồ với:
a) Chiều quay từ tia Om đến tia Ox trong Hình 3a.
b) Chiều quay từ tia Om đến tia Oy trong Hình 3b.

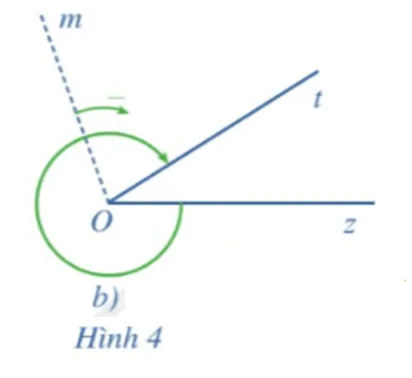
Luyện tập 2 trang 7 Toán 11 Tập 1
Đọc tên góc lượng giác,tia đầu và tia cuối của góc lượng giác đó trong Hình 4b.
Hoạt động 3 trang 7 Toán 11 Tập 1
a) Trong Hình 5a, tia Om quay theo chiều dương đúng một vòng. Hỏi tia đó quét nên một góc bao nhiêu độ?
b) Trong Hình 5b, tia Om quay theo chiều dương ba vòng và một phần tư vòng (tức là 3 vòng). Hỏi tia đó quét nên một góc bao nhiêu độ?
c) Trong Hình 5c, tia Om quay theo chiều âm đúng một vòng. Hỏi tia đó quét nên một góc bao nhiêu độ?

Luyện tập 3 trang 8 Toán 11 Tập 1
Hãy biểu diễn trên mặt phẳng góc lượng giác gốc O có tia đầu Ou, tia cuối Ov và có số đo .
Hoạt động 4 trang 8 Toán 11 Tập 1
Trong Hình 7a, ba góc lượng giác có cùng tia đầu Ou và tia cuối Ov, trong đó Ou ⊥ Ov. Xác định số đo của góc lượng giác trong các Hình 7b, 7c, 7d.

Luyện tập 4 trang 9 Toán 11 Tập 1
Viết công thức biểu thị số đo của các góc lượng giác có cùng tia đầu, tia cuối với góc lượng giác có số đo bằng .
Hoạt động 5 trang 9 Toán 11 Tập 1
Cho góc (hình học) xOz, tia Oy nằm trong góc xOz (Hình 8). Nêu mối liên hệ giữa số đo của góc xOz và tổng số đo của hai góc xOy và yOz.

Luyện tập 5 trang 9 Toán 11 Tập 1
Cho góc lượng giác (Ou, Ov) có số đo là , góc lượng giác (Ou, Ow) có số đo là . Tìm số đo của góc lượng giác (Ov, Ow).
Hoạt động 6 trang 10 Toán 11 Tập 1
a) Trong mặt phẳng toạ độ (định hướng) Oxy, hãy vẽ đường tròn tâm O với bán kính bằng 1.
b) Hãy nêu chiều dương, chiều âm trên đường tròn tâm O với bán kính bằng 1.
Luyện tập 6 trang 10 Toán 11 Tập 1
Xác định điểm N trên đường tròn lượng giác sao cho (OA, ON) = .
Hoạt động 8 trang 11 Toán 11 Tập 1
Xét dấu các giá trị lượng giác của góc lượng giác α = ‒30°.
Luyện tập 8 trang 11 Toán 11 Tập 1
Xét dấu các giá trị lượng giác của góc lượng giác α = .
Hoạt động 9 trang 11 Toán 11 Tập 1
Cho góc lượng giác α. So sánh:
a) cos2α + sin2α và 1;
b) tanα . cotα và 1 (với cosα ≠ 0, sinα ≠ 0);
c) 1 + tan2α và với cosα ≠ 0;
d) 1 + cot2α và với sinα ≠ 0.