Giải bài tập Toán 11 Chương 3: Giới hạn. Hàm số liên tục | Cánh Diều
Hướng dẫn giải Chương 3: Giới hạn. Hàm số liên tục
Giải bài tập Bài 1: Giới hạn của dãy số
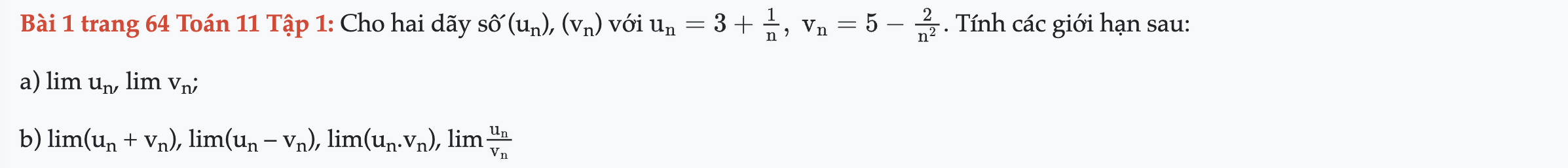
Bài 1 trang 64 Toán 11 Tập 1
Cho hai dãy số (un), (vn). Tính các giới hạn sau. Bài 1 trang 64 Toán 11 Tập 1

Bài 2 trang 65 Toán 11 Tập 1
Tính các giới hạn sau. Bài 2 trang 65 Toán 11 Tập 1

Bài 3 trang 65 Toán 11 Tập 1
Tính tổng của cấp số nhân lùi vô hạn (un), với u1 = 2/3; q = -1/4. Bài 3 trang 65 Toán 11 Tập 1

Bài 4 trang 65 Toán 11 Tập 1
Từ hình vuông có độ dài cạnh bằng 1, người ta nối các trung điểm của cạnh hình vuông để tạo ra hình vuông mới như Hình 3. Tiếp tục quá trình này đến vô hạn. Bài 4 trang 65 Toán 11 Tập 1

Bài 5 trang 65 Toán 11 Tập 1
Có 1 kg chất phóng xạ độc hại. Biết rằng, cứ sau một khoảng thời gian T = 24 000 năm thì một nửa số chất phóng xạ này bị phân ra thành chất khác không độc hại đối với sức khỏe của con người (T được gọi là chu kì bán rã). Bài 5 trang 65 Toán 11 Tập 1

Bài 6 trang 65 Toán 11 Tập 1
Gọi C là nửa đường tròn đường kính AB = 2R. C1 là đường gồm hai nửa đường tròn đường kính AB/2. C2 là đường gồm bốn nửa đường tròn đường kính AB/4. Bài 6 trang 65 Toán 11 Tập 1

Câu hỏi khởi động trang 59 Toán 11 Tập 1
Zénon (Zê – nông, 496 – 429 trước Công Nguyên) là một triết gia Hy Lạp ở thành phố Edée đã phát biểu nghịch lí như sau: Achilles (A – sin) là một lực sĩ trong thần thoại Hy Lạp. Câu hỏi khởi động trang 59 Toán 11 Tập 1

Hoạt động 1 trang 59 Toán 11 Tập 1
Hình 2 biểu diễn các số hạng của dãy số (un), với un = 1/n trên hệ trục tọa độ. Nhận xét về sự thay đổi các giá trị un khi n ngày càng lớn. Hoạt động 1 trang 59 Toán 11 Tập 1

Luyện tập 1 trang 60 Toán 11 Tập 1
Chứng minh rằng lim 0 = 0. Luyện tập 1 trang 60 Toán 11 Tập 1
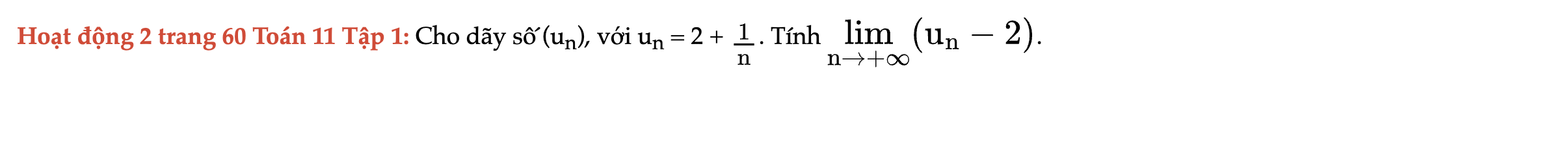
Hoạt động 2 trang 60 Toán 11 Tập 1
Cho dãy số (un), với un = 2 + 1/n. Tính giới hạn sau. Hoạt động 2 trang 60 Toán 11 Tập 1
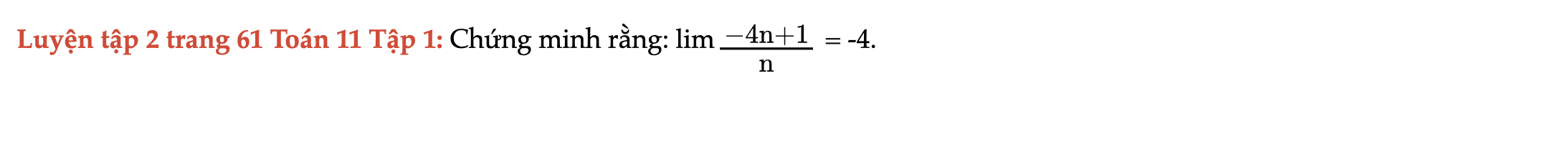
Luyện tập 2 trang 61 Toán 11 Tập 1
Luyện tập 2 trang 61 Toán 11 Tập 1
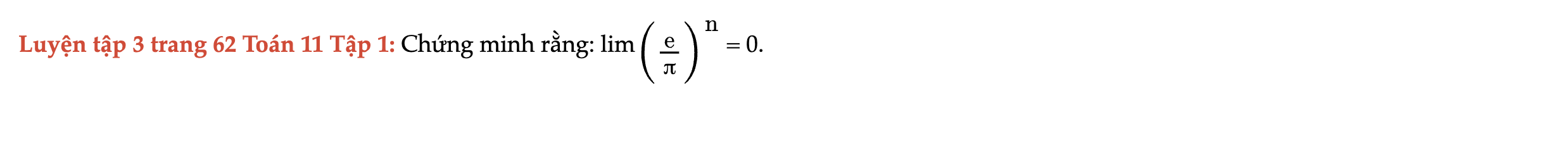
Luyện tập 3 trang 62 Toán 11 Tập 1
Luyện tập 3 trang 62 Toán 11 Tập 1
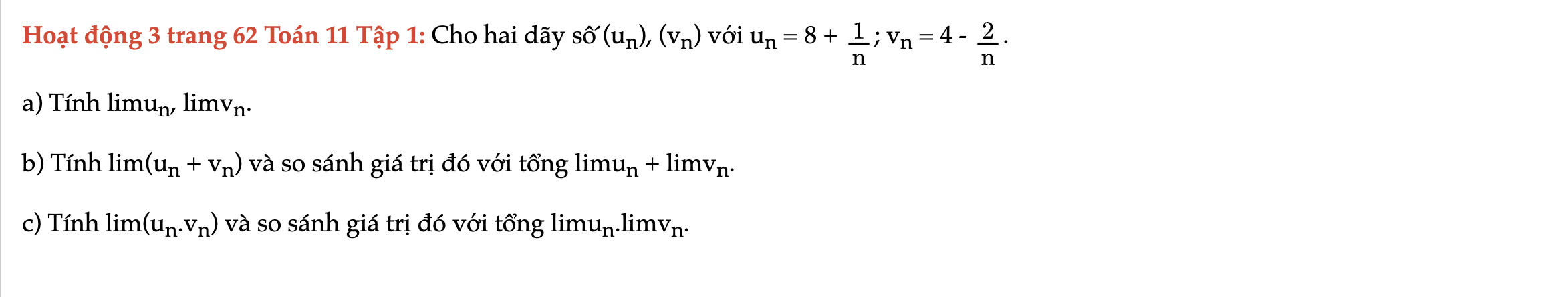
Hoạt động 3 trang 62 Toán 11 Tập 1
Cho hai dãy số (un), (vn). Tính limun, limvn. Tính lim(un + vn) và so sánh giá trị đó với tổng limun + limvn. Hoạt động 3 trang 62 Toán 11 Tập 1

Luyện tập 4 trang 62 Toán 11 Tập 1
Tính các giới hạn sau. Luyện tập 4 trang 62 Toán 11 Tập 1

Hoạt động 4 trang 63 Toán 11 Tập 1
Cho cấp số nhân (un), với u1 = 1 và công bội q = 1/2. Hãy so sánh |q| với 1. Hoạt động 4 trang 63 Toán 11 Tập 1
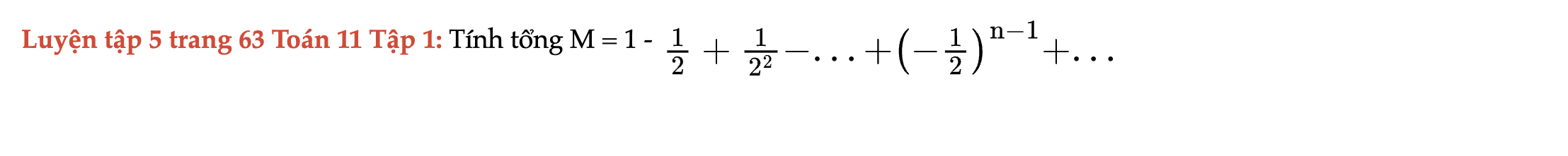
Luyện tập 5 trang 63 Toán 11 Tập 1
Tính tổng M như sau. Luyện tập 5 trang 63 Toán 11 Tập 1

Luyện tập 6 trang 63 Toán 11 Tập 1
Giải thích vì sao nghịch lí Zénon trong phần mở đầu là không đúng. Luyện tập 6 trang 63 Toán 11 Tập 1

Hoạt động 5 trang 63 Toán 11 Tập 1
Quan sát dãy số (un) với un = n^2 và cho biết giá trị của nn có thể lớn hơn một số dương bất kì được hay không kể từ một số hạng nào đó trở đi. Hoạt động 5 trang 63 Toán 11 Tập 1
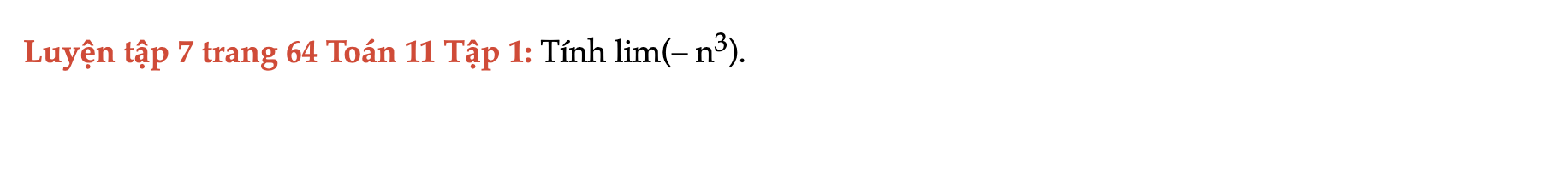
Luyện tập 7 trang 64 Toán 11 Tập 1
Tính lim(– n^3). Luyện tập 7 trang 64 Toán 11 Tập 1
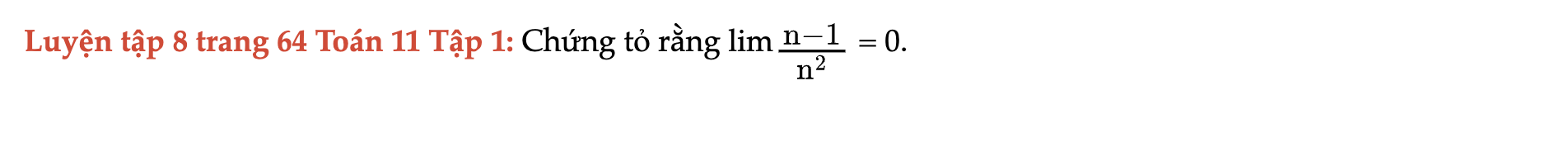
Luyện tập 8 trang 64 Toán 11 Tập 1
Luyện tập 8 trang 64 Toán 11 Tập 1
Giải bài tập Bài 2: Giới hạn của hàm số

Bài 1 trang 72 Toán 11 Tập 1
Sử dụng định nghĩa, tìm các giới hạn sau. Bài 1 trang 72 Toán 11 Tập 1
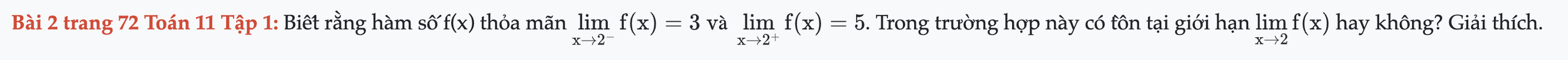
Bài 2 trang 72 Toán 11 Tập 1
Bài 2 trang 72 Toán 11 Tập 1

Bài 3 trang 72 Toán 11 Tập 1
Tính các giới hạn sau. Bài 3 trang 72 Toán 11 Tập 1

Bài 4 trang 72 Toán 11 Tập 1
Tính các giới hạn sau. Bài 4 trang 72 Toán 11 Tập 1
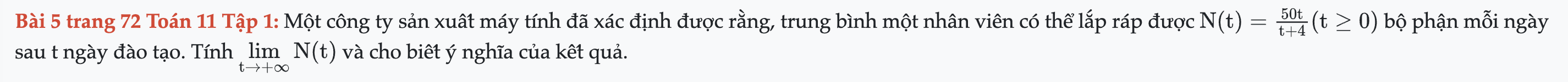
Bài 5 trang 72 Toán 11 Tập 1
Một công ty sản xuất máy tính đã xác định được rằng, trung bình một nhân viên có thể lắp ráp được N(t) bộ phận mỗi ngày sau t ngày đào tạo. Bài 5 trang 72 Toán 11 Tập 1

Bài 6 trang 72 Toán 11 Tập 1
Chi phí (đơn vị: nghìn đồng) để sản xuất x sản phẩm của một công ty được xác định bởi hàm số: C(x) = 50 000 + 105x. Bài 6 trang 72 Toán 11 Tập 1

Câu hỏi khởi động trang 65 Toán 11 Tập 1
Hình 5 biểu diễn đồ thị hàm số vận tốc theo biến số t (t là thời gian, đơn vị: giây). Khi các giá trị của biến số t dần tới 0,2 (s) thì các giá trị tương ứng của hàm số v(t) dần tới 0,070 (m/s). Câu hỏi khởi động trang 65 Toán 11 Tập 1

Hoạt động 1 trang 65 Toán 11 Tập 1
Xét hàm số f(x) = 2x. Xét dãy số (xn), với xn = 1 + 1/n. Hoàn thành bảng giá trị f(xn) tướng ứng. Hoạt động 1 trang 65 Toán 11 Tập 1

Luyện tập 1 trang 67 Toán 11 Tập 1
Sử dụng định nghĩa, chứng minh giới hạn sau. Luyện tập 1 trang 67 Toán 11 Tập 1
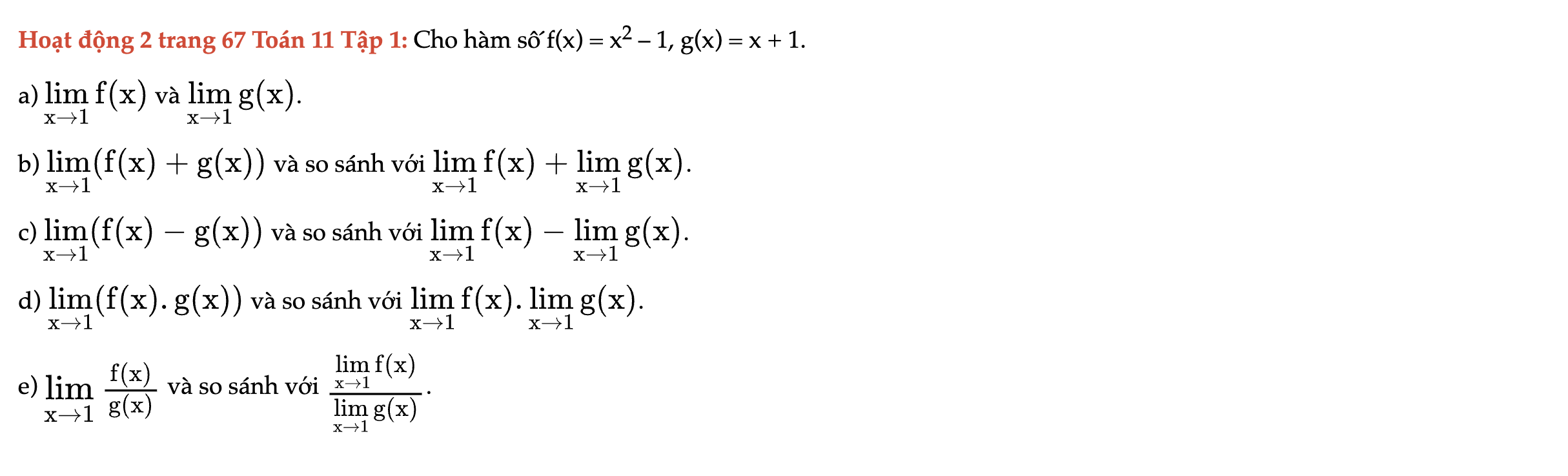
Hoạt động 2 trang 67 Toán 11 Tập 1
Hoạt động 2 trang 67 Toán 11 Tập 1

Luyện tập 2 trang 68 Toán 11 Tập 1
Tính các giới hạn sau. Luyện tập 2 trang 68 Toán 11 Tập 1

Hoạt động 3 trang 68 Toán 11 Tập 1
Cho hàm số f(x) có đồ thị ở Hình 6. Xét dãy số (un) sao cho un < 0 và lim un = 0. Xác định f(un) và tìm lim f(un). Hoạt động 3 trang 68 Toán 11 Tập 1
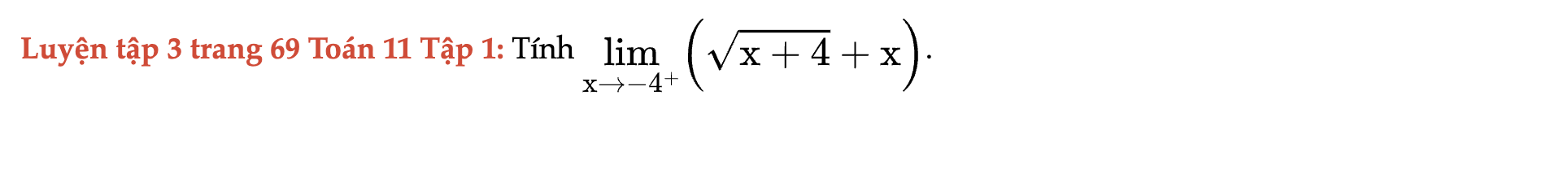
Luyện tập 3 trang 69 Toán 11 Tập 1
Tính giới hạn sau. Luyện tập 3 trang 69 Toán 11 Tập 1

Hoạt động 4 trang 69 Toán 11 Tập 1
Cho hàm số f(x) = 1/x (x ≠ 0) có đồ thị như ở Hình 7. Quan sát đồ thị đó và cho biết. Khi biến x dần tới dương vô cực thì f(x) dần tới giá trị nào. Hoạt động 4 trang 69 Toán 11 Tập 1
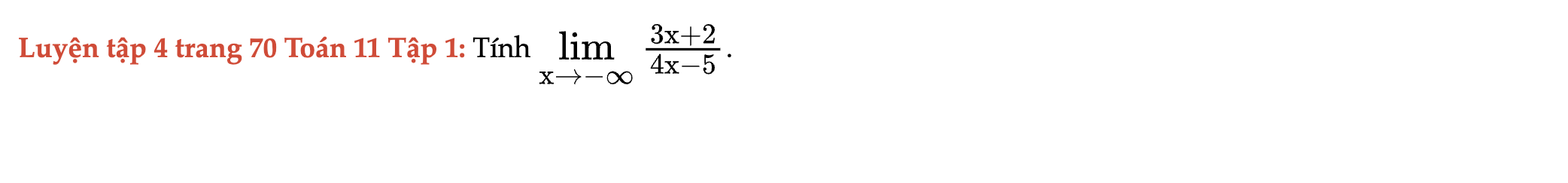
Luyện tập 4 trang 70 Toán 11 Tập 1
Tính giới hạn sau. Luyện tập 4 trang 70 Toán 11 Tập 1

Hoạt động 5 trang 70 Toán 11 Tập 1
Cho hàm số f(x) = 1/(x+1) (x ≠ 1) có đồ thị như Hình 8. Quan sát đồ thị đó và cho biết. Khi biến x dần tới 1 về bên phải thì f(x) dần tới đâu. Hoạt động 5 trang 70 Toán 11 Tập 1
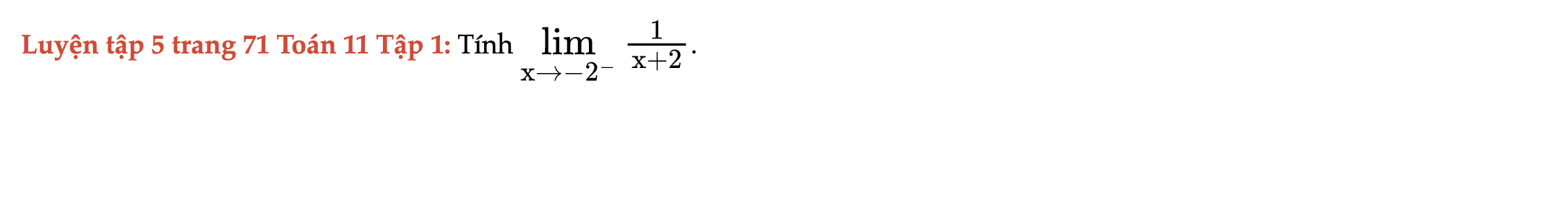
Luyện tập 5 trang 71 Toán 11 Tập 1
Tính giới hạn sau. Luyện tập 5 trang 71 Toán 11 Tập 1

Hoạt động 6 trang 71 Toán 11 Tập 1
Cho hàm số f(x) = x có đồ thị như Hình 9. Quan sát đồ thị đó và cho biết. Khi biến x dần tới dương vô cực thì f(x) dần tới đâu. Hoạt động 6 trang 71 Toán 11 Tập 1
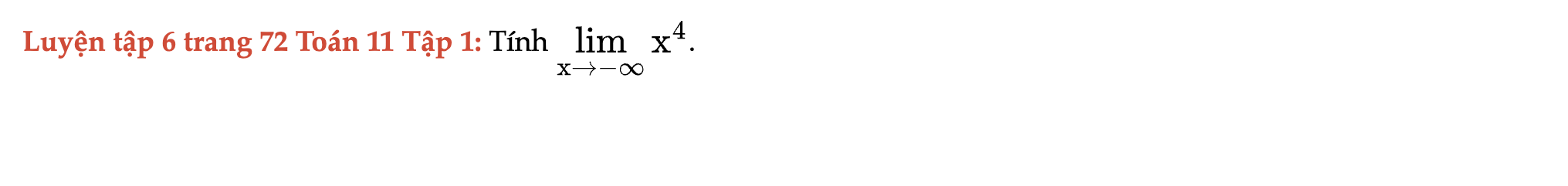
Luyện tập 6 trang 72 Toán 11 Tập 1
Tính giới hạn sau. Luyện tập 6 trang 72 Toán 11 Tập 1
Giải bài tập Bài 3: Hàm số liên tục
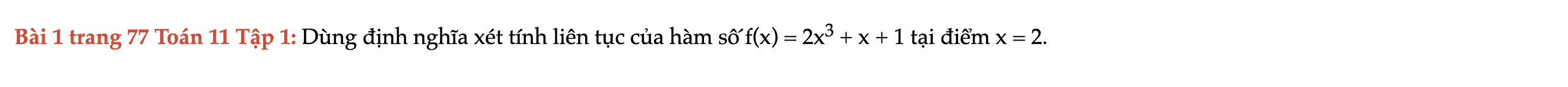
Bài 1 trang 77 Toán 11 Tập 1
Dùng định nghĩa xét tính liên tục của hàm số f(x) = 2x^3 + x + 1 tại điểm x = 2. Bài 1 trang 77 Toán 11 Tập 1
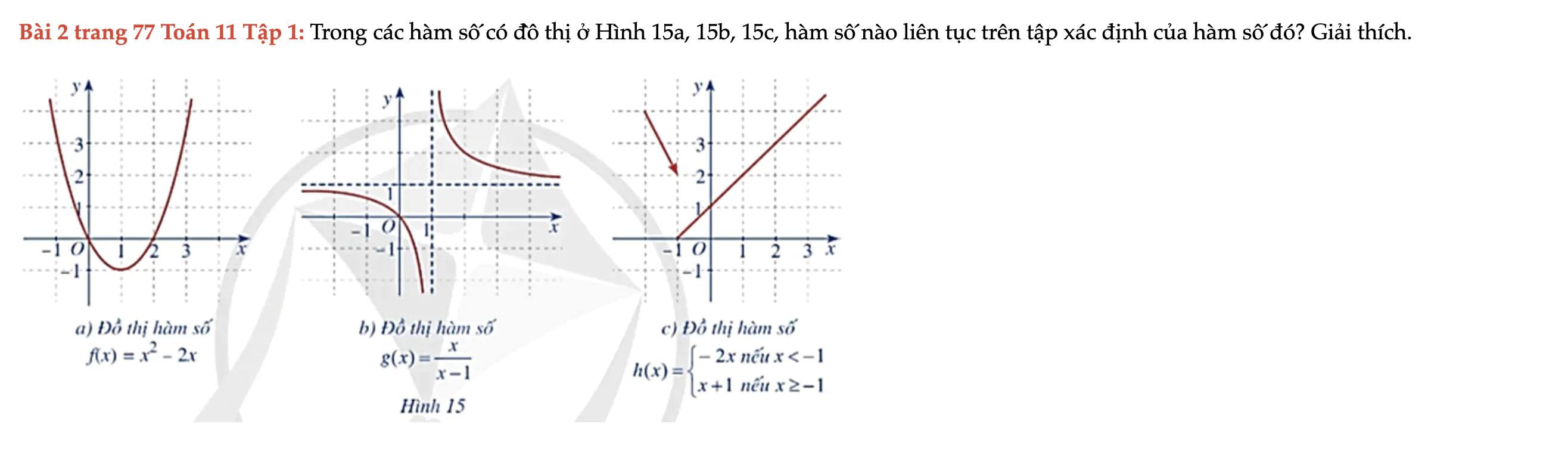
Bài 2 trang 77 Toán 11 Tập 1
Trong các hàm số có đồ thị ở Hình 15a, 15b, 15c, hàm số nào liên tục trên tập xác định của hàm số đó? Giải thích. Bài 2 trang 77 Toán 11 Tập 1

Bài 3 trang 77 Toán 11 Tập 1
Bạn Nam cho rằng: “Nếu hàm số y = f(x) liên tục tại điểm x0, còn hàm số y = g(x) không liên tục tại x0, thì hàm số y = f(x) + g(x) không liên tục tại x0”. Theo em, ý kiến của bạn Nam đúng hay sai? Giải thích. Bài 3 trang 77 Toán 11 Tập 1

Bài 4 trang 77 Toán 11 Tập 1
Xét tính liên tục của mỗi hàm số sau trên tập xác định của hàm số đó. Bài 4 trang 77 Toán 11 Tập 1
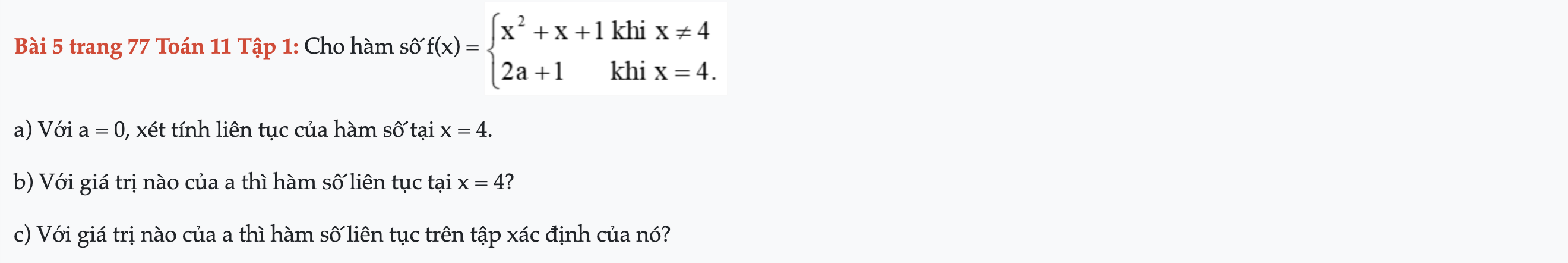
Bài 5 trang 77 Toán 11 Tập 1
Cho hàm số f(x), với a = 0, xét tính liên tục của hàm số tại x = 4. Bài 5 trang 77 Toán 11 Tập 1

Bài 6 trang 77 Toán 11 Tập 1
Hình 16 biểu thị độ cao h(m) của một quả bóng đá lên theo thời gian t(s), trong đó h(t) = – 2t^2 + 8t. Chứng tỏ hàm số h(t) liên tục trên tập xác định. Bài 6 trang 77 Toán 11 Tập 1

Câu hỏi khởi động trang 73 Toán 11 Tập 1
Cầu sông Hàn là một trong những cây cầu bắc qua sông Hàn ở Đà Nẵng. Đây là cây cầu đầu tiên do kĩ sư, công nhân Việt Nam tự thiết kế và thi công. Câu hỏi khởi động trang 73 Toán 11 Tập 1

Hoạt động 1 trang 73 Toán 11 Tập 1
Quan sát đồ thị hàm số f(x) = x ở Hình 11. Tính giới hạn sau. Hoạt động 1 trang 73 Toán 11 Tập 1
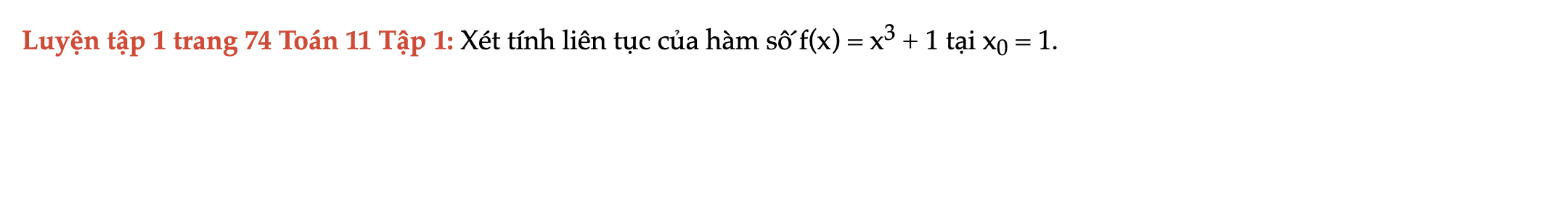
Luyện tập 1 trang 74 Toán 11 Tập 1
Xét tính liên tục của hàm số f(x). Luyện tập 1 trang 74 Toán 11 Tập 1

Hoạt động 2 trang 74 Toán 11 Tập 1
Cho hàm số f(x) = x + 1 với x ∈ ℝ. Giả sử x0 ∈ ℝ. Hàm= số f(x) có liên tục tại điểm x0 hay không? Hoạt động 2 trang 74 Toán 11 Tập 1
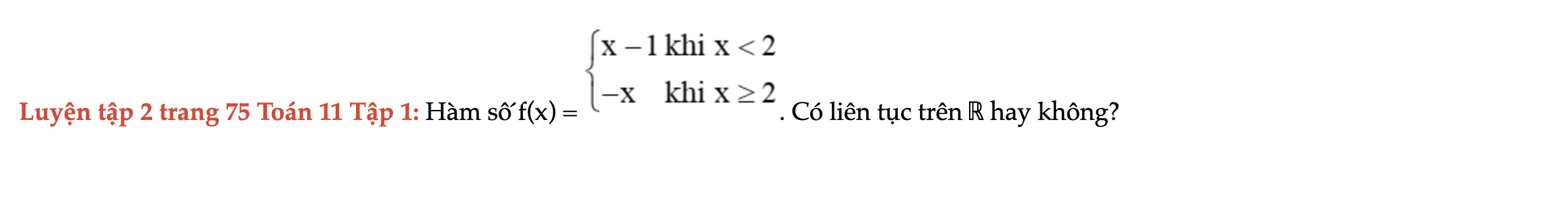
Luyện tập 2 trang 75 Toán 11 Tập 1
Hàm số f(x) có liên tục trên ℝ hay không? Luyện tập 2 trang 75 Toán 11 Tập 1
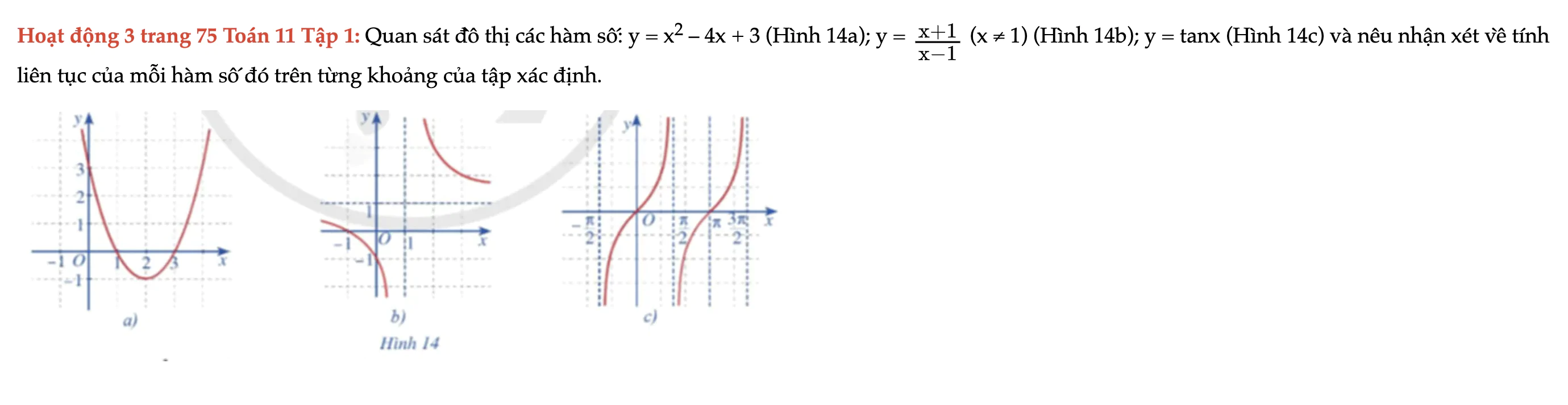
Hoạt động 3 trang 75 Toán 11 Tập 1
Quan sát đồ thị các hàm số sau và nêu nhận xét về tính liên tục của mỗi hàm số đó trên từng khoảng của tập xác định. Hoạt động 3 trang 75 Toán 11 Tập 1

Luyện tập 3 trang 76 Toán 11 Tập 1
Hàm f(x) có liên tục trên mỗi khoảng (– ∞; 8), (8; + ∞) hay không? Luyện tập 3 trang 76 Toán 11 Tập 1
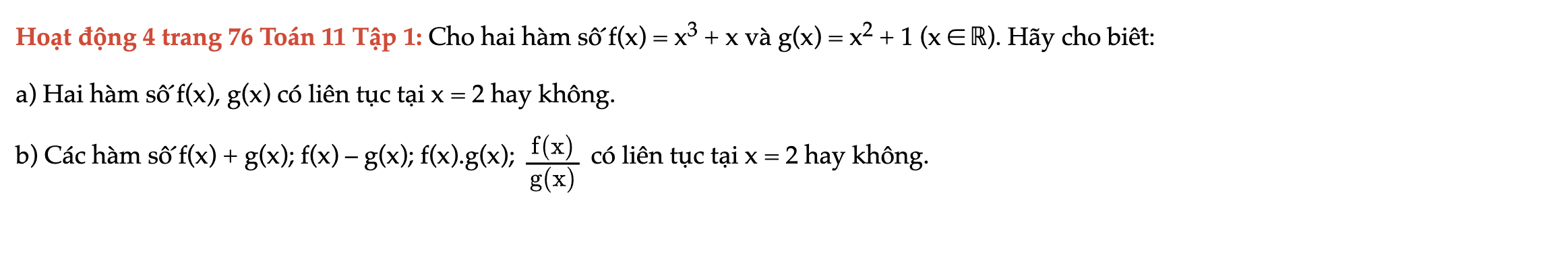
Hoạt động 4 trang 76 Toán 11 Tập 1
Cho hai hàm số f(x) và g(x). Hãy cho biết hai hàm số f(x), g(x) có liên tục tại x = 2 hay không. Hoạt động 4 trang 76 Toán 11 Tập 1
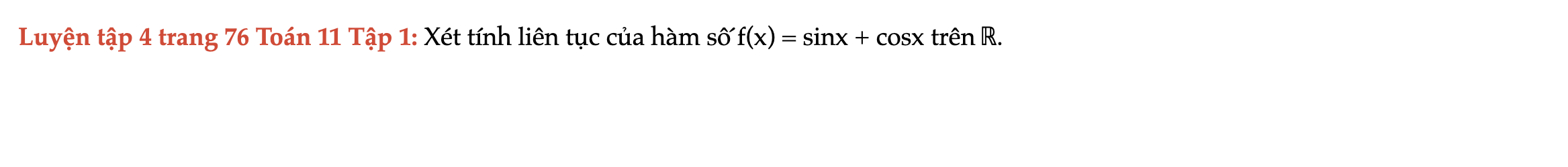
Luyện tập 4 trang 76 Toán 11 Tập 1
Xét tính liên tục của hàm số f(x) = sinx + cosx trên ℝ. Luyện tập 4 trang 76 Toán 11 Tập 1
Giải bài tập Bài tập cuối chương 3
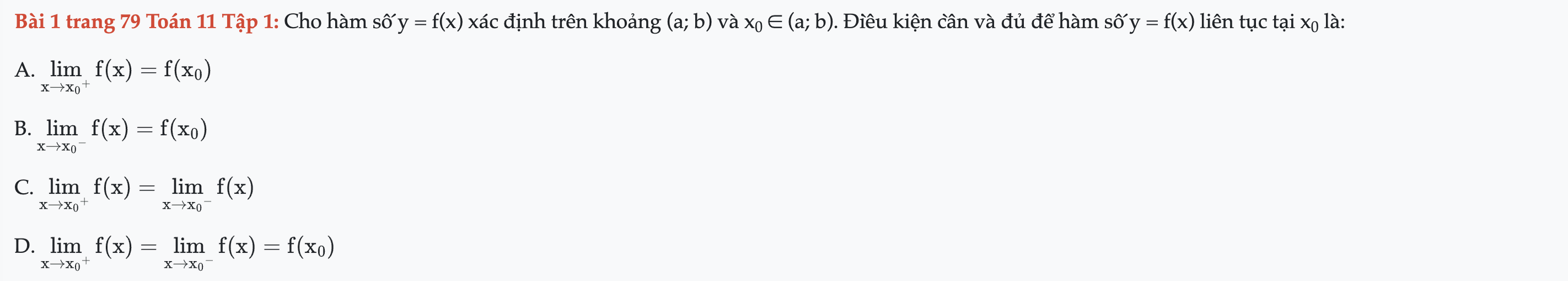
Bài 1 trang 79 Toán 11 Tập 1
Cho hàm số y = f(x) xác định trên khoảng (a; b) và x0 ∈ (a; b). Điều kiện cần và đủ để hàm số y = f(x) liên tục tại x0 là. Bài 1 trang 79 Toán 11 Tập 1

Bài 2 trang 79 Toán 11 Tập 1
Tính các giới hạn sau. Bài 2 trang 79 Toán 11 Tập 1

Bài 3 trang 79 Toán 11 Tập 1
Tính các giới hạn sau. Bài 3 trang 79 Toán 11 Tập 1

Bài 4 trang 79 Toán 11 Tập 1
Tính các giới hạn sau. Bài 4 trang 79 Toán 11 Tập 1

Bài 5 trang 79 Toán 11 Tập 1
Cho hàm số f(x), với a = 0, b = 1, xét tính liên tục của hàm số tại x = 2. Bài 5 trang 79 Toán 11 Tập 1

Bài 6 trang 80 Toán 11 Tập 1
Từ độ cao 55,8 m của tháp nghiêng Pisa nước Ý, người ta thả một quả bóng cao su chạm xuống đất (Hình 18). Giả sử mỗi lần chạm đất quả bóng lại này lên độ cao bằng 1/10 độ cao mà quả bóng đạt được trước đó. Bài 6 trang 80 Toán 11 Tập 1
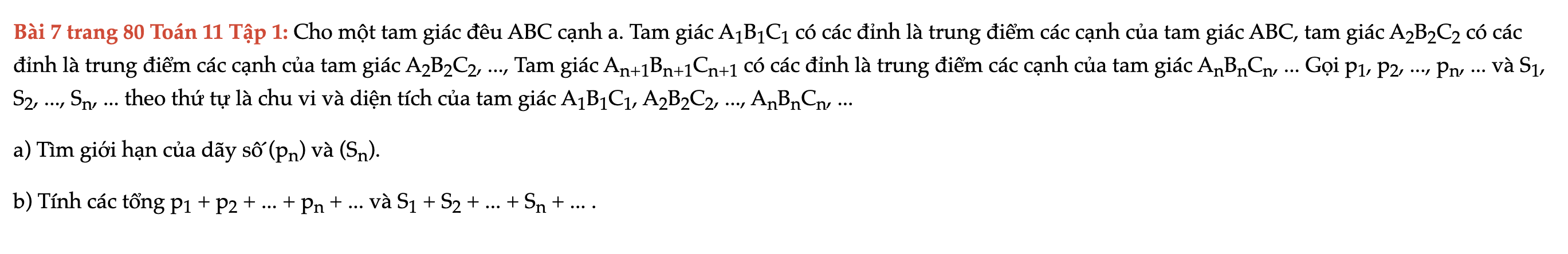
Bài 7 trang 80 Toán 11 Tập 1
Cho một tam giác đều ABC cạnh a. Tam giác A1B1C1 có các đỉnh là trung điểm các cạnh của tam giác ABC, tam giác A2B2C2 có các đỉnh là trung điểm các cạnh của tam giác A2B2C2, ... Bài 7 trang 80 Toán 11 Tập 1
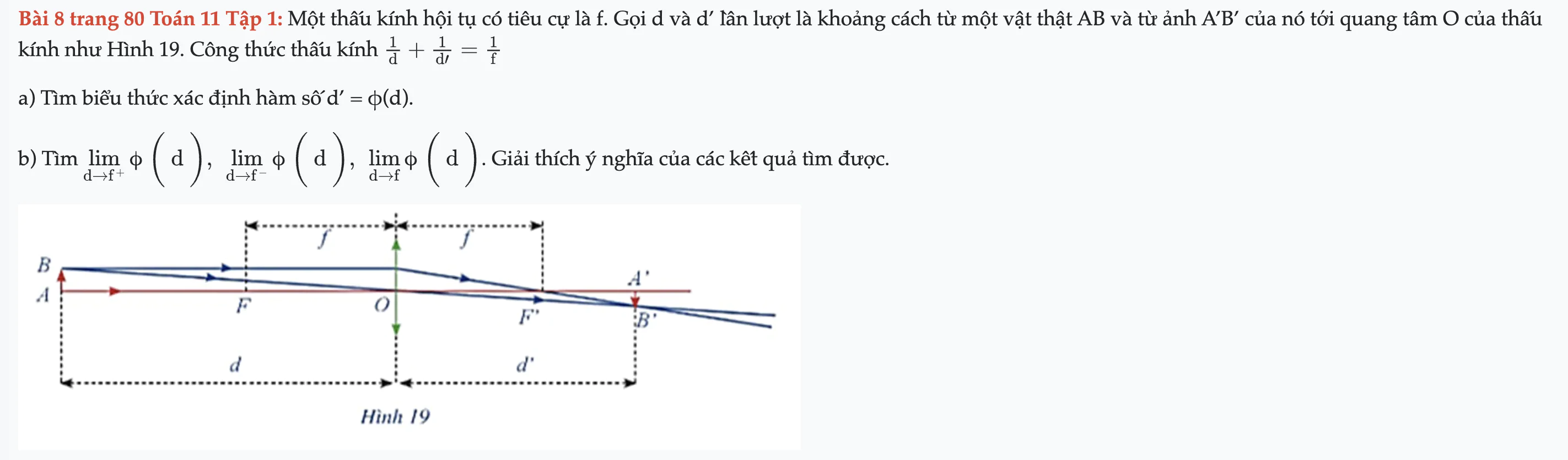
Bài 8 trang 80 Toán 11 Tập 1
Một thấu kính hội tụ có tiêu cự là f. Gọi d và d’ lần lượt là khoảng cách từ một vật thật AB và từ ảnh A’B’ của nó tới quang tâm O của thấu kính như Hình 19. Công thức thấu kính 1/d + 1/d' = 1/f. Bài 8 trang 80 Toán 11 Tập 1