Giải bài tập Luyện tập 4 trang 76 Toán 11 Tập 1 | Toán 11 - Cánh diều
Hướng dẫn giải chi tiết từng bước bài tập Luyện tập 4 trang 76 Toán 11 Tập 1. Bài 3: Hàm số liên tục. Toán 11 - Cánh diều
Đề bài:
Xét tính liên tục của hàm số f(x) = sinx + cosx trên ℝ.
Đáp án và cách giải chi tiết:
Hàm số sinx và cosx liên tục trên ℝ.
Do đó hàm số y = sinx + cosx liên tục trên ℝ.
Nguồn: loigiaitoan.com
Tổng số đánh giá:
Xếp hạng: / 5 sao
Bài tập liên quan:
Bài 1 trang 77 Toán 11 Tập 1
Dùng định nghĩa xét tính liên tục của hàm số f(x) = 2x3 + x + 1 tại điểm x = 2.
Bài 2 trang 77 Toán 11 Tập 1
Trong các hàm số có đồ thị ở Hình 15a, 15b, 15c, hàm số nào liên tục trên tập xác định của hàm số đó? Giải thích.
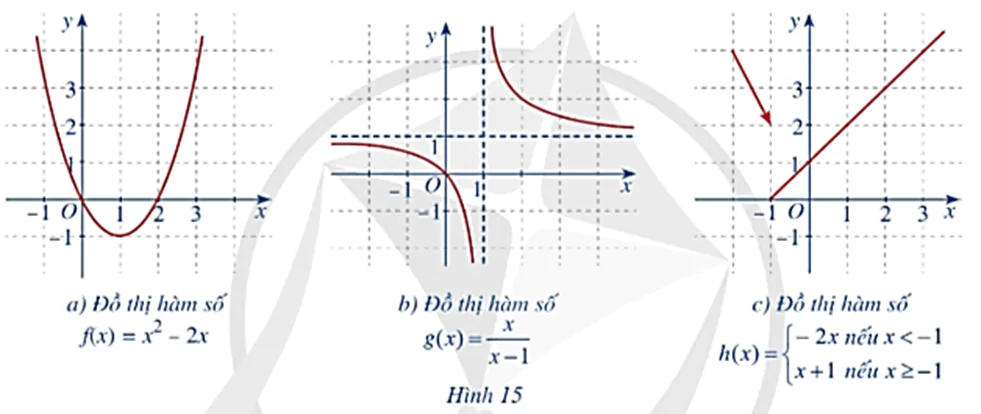
Bài 3 trang 77 Toán 11 Tập 1
Bạn Nam cho rằng: “Nếu hàm số y = f(x) liên tục tại điểm x0, còn hàm số y = g(x) không liên tục tại x0, thì hàm số y = f(x) + g(x) không liên tục tại x0”. Theo em, ý kiến của bạn Nam đúng hay sai? Giải thích.
Bài 4 trang 77 Toán 11 Tập 1
Xét tính liên tục của mỗi hàm số sau trên tập xác định của hàm số đó:
a) f(x) = x2 + sinx;
b) g(x) = x4 – x2 + ;
c) h(x) = .
Bài 5 trang 77 Toán 11 Tập 1
Cho hàm số f(x) = 
a) Với a = 0, xét tính liên tục của hàm số tại x = 4.
b) Với giá trị nào của a thì hàm số liên tục tại x = 4?
c) Với giá trị nào của a thì hàm số liên tục trên tập xác định của nó?
Bài 6 trang 77 Toán 11 Tập 1
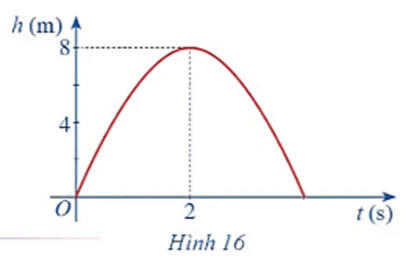
Hình 16 biểu thị độ cao h(m) của một quả bóng đá lên theo thời gian t(s), trong đó h(t) = – 2t2 + 8t.
a) Chứng tỏ hàm số h(t) liên tục trên tập xác định.
b) Dựa vào đồ thị hãy xác định .
Câu hỏi khởi động trang 73 Toán 11 Tập 1
Cầu sông Hàn là một trong những cây cầu bắc qua sông Hàn ở Đà Nẵng. Đây là cây cầu đầu tiên do kĩ sư, công nhân Việt Nam tự thiết kế và thi công. Khi cầu không quay (Hình 10a), mặt cầu liền mạch nên các phương tiện có thể đi lại giữa hai đầu cầu. Khi cầu quay (Hình 10b) để các tàu, thuyền có thể đi qua thì mặt cầu không còn liền mạch nữa, các phương tiện không thể đi qua giữa hai đầu cầu.
Kiến thức gì trong toán học thể hiện chuyển động có đường đi là đường liền mạch?

Hoạt động 1 trang 73 Toán 11 Tập 1
Quan sát đồ thị hàm số f(x) = x ở Hình 11.

a) Tính .
b) và f(1).
Luyện tập 1 trang 74 Toán 11 Tập 1
Xét tính liên tục của hàm số f(x) = x3 + 1 tại x0 = 1.
Hoạt động 2 trang 74 Toán 11 Tập 1
Cho hàm số f(x) = x + 1 với x ∈ ℝ.
a) Giả sử x0 ∈ ℝ. Hàm= số f(x) có liên tục tại điểm x0 hay không?
b) Quan sát đồ thị hàm số f(x) = x + 1 với x ∈ ℝ (Hình 13), nêu nhận xét về đặc điểm của đồ thị hàm số đó.

Luyện tập 2 trang 75 Toán 11 Tập 1
Hàm số f(x) = 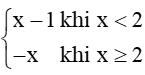
Hoạt động 3 trang 75 Toán 11 Tập 1
Quan sát đồ thị các hàm số: y = x2 – 4x + 3 (Hình 14a); y = (x ≠ 1) (Hình 14b); y = tanx (Hình 14c) và nêu nhận xét về tính liên tục của mỗi hàm số đó trên từng khoảng của tập xác định.

Luyện tập 3 trang 76 Toán 11 Tập 1
Hàm f(x) = có liên tục trên mỗi khoảng (– ∞; 8), (8; + ∞) hay không?
Hoạt động 4 trang 76 Toán 11 Tập 1
Cho hai hàm số f(x) = x3 + x và g(x) = x2 + 1 (x ∈ ℝ). Hãy cho biết:
a) Hai hàm số f(x), g(x) có liên tục tại x = 2 hay không.
b) Các hàm số f(x) + g(x); f(x) – g(x); f(x).g(x); có liên tục tại x = 2 hay không.