Giải bài tập Hoạt động 1 trang 65 Toán 11 Tập 1 | Toán 11 - Cánh diều
Hướng dẫn giải chi tiết từng bước bài tập Hoạt động 1 trang 65 Toán 11 Tập 1. Bài 2: Giới hạn của hàm số. Toán 11 - Cánh diều
Đề bài:
Xét hàm số f(x) = 2x.
a) Xét dãy số (xn), với xn = 1 + . Hoàn thành bảng giá trị f(xn) tướng ứng.

Các giá trị tương ứng của hàm số f(x1), f(x2), ..., f(xn), ... lập thành một dãy số mà ta kí hiệu là (f(xn)). Tìm limf(xn).
b) Chứng minh rằng với dãy số bất kì (xn), xn → 1 ta luôn có f(xn) → 2.
Đáp án và cách giải chi tiết:
a) Ta có bảng giá trị sau:
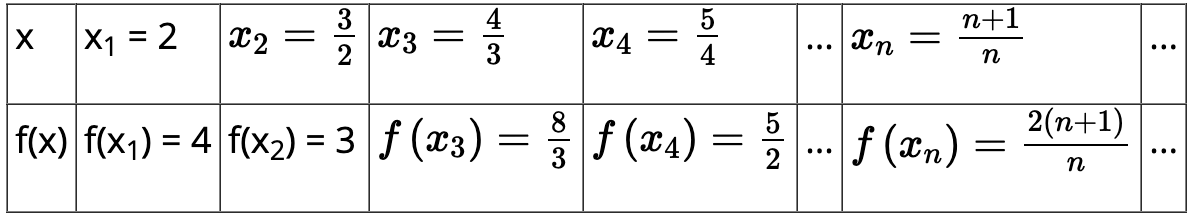
Ta có: limf(xn) = lim = 2.
b) Lấy dãy (xn) bất kí thỏa mãn xn → 1 ta có:
f(xn) = 2xn
⇒ limf(xn) = lim2xn = 2lim xn = 2.1 = 2.
Nguồn: loigiaitoan.com
Tổng số đánh giá:
Xếp hạng: / 5 sao
Bài tập liên quan:
Bài 5 trang 72 Toán 11 Tập 1
Một công ty sản xuất máy tính đã xác định được rằng, trung bình một nhân viên có thể lắp ráp được bộ phận mỗi ngày sau t ngày đào tạo. Tính và cho biết ý nghĩa của kết quả.
Bài 6 trang 72 Toán 11 Tập 1
Chi phí (đơn vị: nghìn đồng) để sản xuất x sản phẩm của một công ty được xác định bởi hàm số: C(x) = 50 000 + 105x.
a) Tính chi phí trung bình để sản xuất một sản phẩm.
b) Tính và cho biết ý nghĩa của kết quả.
Bài 2 trang 72 Toán 11 Tập 1
Biết rằng hàm số f(x) thỏa mãn . Trong trường hợp này có tồn tại giới hạn hay không? Giải thích.
Câu hỏi khởi động trang 65 Toán 11 Tập 1
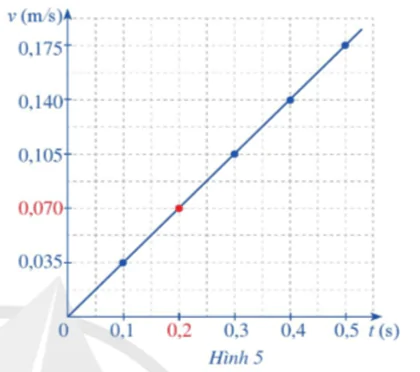
Hình 5 biểu diễn đồ thị hàm số vận tốc theo biến số t (t là thời gian, đơn vị: giây). Khi các giá trị của biến số t dần tới 0,2 (s) thì các giá trị tương ứng của hàm số v(t) dần tới 0,070 (m/s).
Trong toán học, giá trị 0,070 biểu thị khái niệm gì của hàm số v(t) khi các giá trị của biến số t dần tới 0,2?
Hoạt động 2 trang 67 Toán 11 Tập 1
Cho hàm số f(x) = x2 – 1, g(x) = x + 1.
a) và .
b) và so sánh với .
c) và so sánh với .
d) và so sánh với .
e) và so sánh với .
Hoạt động 3 trang 68 Toán 11 Tập 1
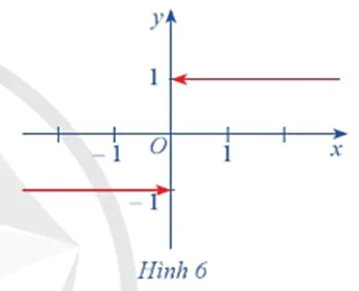
Cho hàm số  . Hàm số f(x) có đồ thị ở Hình 6.
. Hàm số f(x) có đồ thị ở Hình 6.
a) Xét dãy số (un) sao cho un < 0 và lim un = 0. Xác định f(un) và tìm lim f(un).
b) Xét dãy số (vn) sao cho vn > 0 và lim vn = 0. Xác định f(vn) và tìm lim f(vn).
Hoạt động 4 trang 69 Toán 11 Tập 1
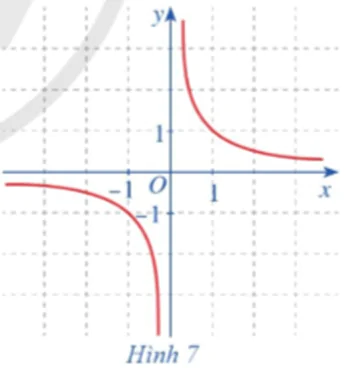
Cho hàm số f(x) = (x ≠ 0) có đồ thị như ở Hình 7. Quan sát đồ thị đó và cho biết:
a) Khi biến x dần tới dương vô cực thì f(x) dần tới giá trị nào.
b) Khi biến x dần tới âm vô cực thì f(x) dần tới giá trị nào.
Hoạt động 5 trang 70 Toán 11 Tập 1
Cho hàm số f(x) = (x ≠ 1) có đồ thị như Hình 8. Quan sát đồ thị đó và cho biết:
a) Khi biến x dần tới 1 về bên phải thì f(x) dần tới đâu.
b) Khi biến x dần tới 1 về bên trái thì f(x) dần tới đâu.

Hoạt động 6 trang 71 Toán 11 Tập 1
Cho hàm số f(x) = x có đồ thị như Hình 9. Quan sát đồ thị đó và cho biết:
a) Khi biến x dần tới dương vô cực thì f(x) dần tới đâu.
b) Khi biến x dần tới âm vô cực thì f(x) dần tới đâu.

Bài 4 trang 72 Toán 11 Tập 1
Tính các giới hạn sau:
a) 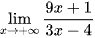 ;
;
b) 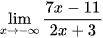 ;
;
c) 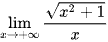 ;
;
d) 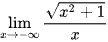 ;
;
e) 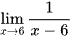 ;
;
f) 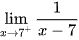 .
.
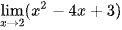 ;
;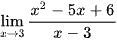 ;
;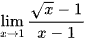 .
.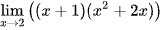 ;
;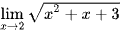 .
.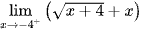 .
.