Giải bài tập Bài 2 trang 79 Toán 11 Tập 2 | Toán 11 - Cánh diều
Hướng dẫn giải chi tiết từng bước bài tập Bài 2 trang 79 Toán 11 Tập 2. Bài 1: Hai đường thẳng vuông góc. Toán 11 - Cánh diều
Đề bài:
Trong Hình 7 cho ABB’A’, BCC’B’, ACC’A’ là các hình chữ nhật. Chứng minh rằng AB ⊥ CC’, AA’ ⊥ BC.

Đáp án và cách giải chi tiết:
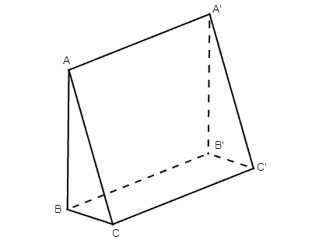
⦁ Do ABB’A’ là hình chữ nhật nên AB ⊥ BB’.
Do BCC’B’ là hình chữ nhật nên CC’ // BB’.
Từ đó ta có AB ⊥ CC’.
⦁ Do BCC’B’ là hình chữ nhật nên BC ⊥ CC’.
Do AA'C'C là hình chữ nhật nên AA’ // CC’.
Từ đó ta có BC ⊥ AA’ hay AA’ ⊥ BC.
Nguồn: loigiaitoan.com
Tổng số đánh giá:
Xếp hạng: / 5 sao
Bài tập liên quan:
Bài 1 trang 79 Toán 11 Tập 2
Hình 6 gợi nên hình ảnh 5 cặp đường thẳng vuông góc. Hãy chỉ ra 5 cặp đường thẳng đó.

Bài 4 trang 79 Toán 11 Tập 2
Bạn Hoa nói rằng: “Nếu hai đường thẳng phân biệt a và b cùng vuông góc với đường thẳng c thì a và b vuông góc với nhau”. Bạn Hoa nói đúng hay sai? Vì sao?
Câu hỏi khởi động trang 77 Toán 11 Tập 2
Trong Hình 1, hai đường thẳng a, b gợi nên hình ảnh hai đường thẳng vuông góc trong không gian.

Trong không gian, thế nào là hai đường thẳng vuông góc với nhau?
Hoạt động 1 trang 77 Toán 11 Tập 2
Trong mặt phẳng cho hai đường thẳng a, b.
a) Nếu a và b cắt nhau tại điểm O (Hình 2) thì góc giữa hai đường thẳng a, b được xác định như thế nào?
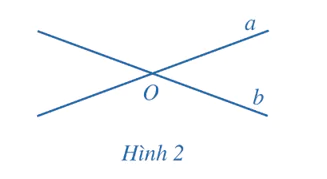
b) Nếu a // b thì góc giữa a và b bằng bao nhiêu độ?
c) Nếu a và b trùng nhau thì góc giữa a và b bằng bao nhiêu độ?
Luyện tập 1 trang 78 Toán 11 Tập 2
Cho tứ diện ABCD có M, N, P lần lượt là trung điểm của AB, BC, DA. Biết tam giác MNP đều. Tính góc giữa hai đường thẳng AC và BD.
Hoạt động 2 trang 78 Toán 11 Tập 2
Trong Hình 1 ở phần mở đầu, hai đường thẳng a, b gợi nên hình ảnh hai đường thẳng vuông góc. Góc giữa a và b bằng bao nhiêu độ?
Luyện tập 2 trang 79 Toán 11 Tập 2
Cho hình lăng trụ ABC.A’B’C’ có H là trực tâm của tam giác ABC. Chứng minh rằng AH ⊥ B’C’.
Bài 3 trang 79 Toán 11 Tập 2
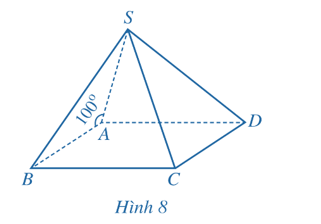
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và 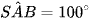 (Hình 8). Tính góc giữa hai đường thẳng:
(Hình 8). Tính góc giữa hai đường thẳng:
a) SA và AB;
b) SA và CD.