Giải bài tập Toán 12 Chương 1. Ứng dụng đạo hàm để khảo sát hàm số | Chân trời sáng tạo
Hướng dẫn giải chi tiết từng bước bài tập thuộc Chương I. Ứng dụng đạo hàm để khảo sát hàm số. Đạo hàm, bảng biến thiên, đồng biến nghịch biến, cực trị, min, max, tiệm cận đứng, tiệm cận ngang, tiệm cận xiên sách giáo khoa Chân trời sáng tạo.
Giải bài tập Bài 1. Tính đơn điệu và cực trị của hàm số.
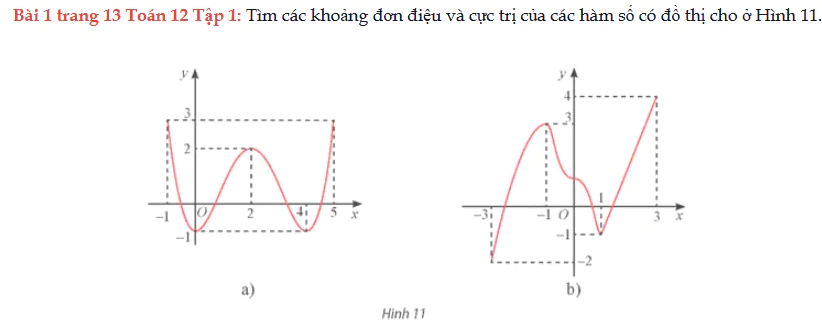
Bài 1 trang 13 Toán 12 Tập 1
Tìm các khoảng đơn điệu và cực trị của các hàm số có đồ thị cho ở Hình 11. Bài 1 trang 13 Toán 12 Tập 1
Bài 2 trang 13 Toán 12 Tập 1
Xét tính đơn điệu và tìm điểm cực trị của các hàm số sau. Bài 2 trang 13 Toán 12 Tập 1

Bài 3 trang 13 Toán 12 Tập 1
Tìm cực trị của các hàm số sau. Bài 3 trang 13 Toán 12 Tập 1

Bài 4 trang 13 Toán 12 Tập 1
Chứng minh rằng hàm số y = f(x) nghịch biến trên từng khoảng xác định của nó. Bài 4 trang 13 Toán 12 Tập 1

Bài 5 trang 13 Toán 12 Tập 1
Kim ngạch xuất khẩu rau quả của Việt Nam trong các năm từ 2010 và 2017 có thể được tính xấp xỉ bằng công thức sau với x là số năm tính từ 2010 đến 2017. Bài 5 trang 13 Toán 12 Tập 1

Bài 6 trang 13 Toán 12 Tập 1
Xét một chất điểm chuyển động dọc theo trục Ox. Tọa độ của chất điểm tại thời điểm t được xác định bởi hàm số x(t). Bài 6 trang 13 Toán 12 Tập 1
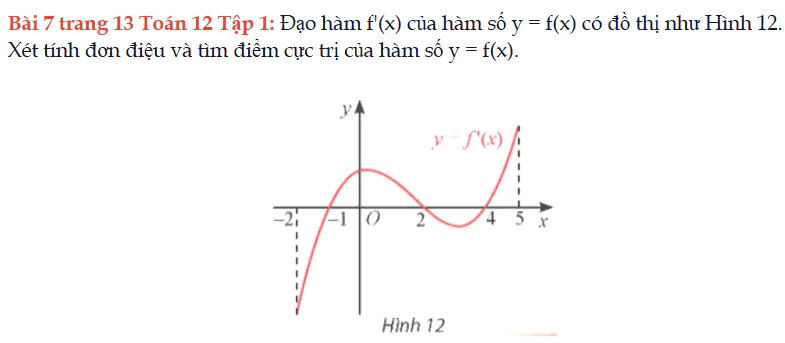
Bài 7 trang 13 Toán 12 Tập 1
Đạo hàm f'(x) của hàm số y = f(x) có đồ thị như Hình 12. Xét tính đơn điệu và tìm điểm cực trị của hàm số y = f(x). Bài 7 trang 13 Toán 12 Tập 1

Hoạt động khởi động trang 6 Toán 12 Tập 1
Trong 8 phút đầu kể từ khi xuất phát, độ cao h (tính bằng mét) của khinh khí cầu vào thời điểm t phút được cho bởi công thức h(t) = 6t^3 – 81t^2 + 324t. Đồ thị của hàm số h(t) được biểu diễn trong hình bên. Hoạt động khởi động trang 6 Toán 12 Tập 1

Thực hành 1 trang 7 Toán 12 Tập 1
Tìm các khoảng đơn điệu của hàm số y = f(x) có đồ thị cho ở Hình 3. Thực hành 1 trang 7 Toán 12 Tập 1

Hoạt động khám phá 1 trang 7 Toán 12 Tập 1
Cho hàm số y = f(x) = x^2. Từ đồ thị của hàm số y = f(x) (Hình 4), hãy chỉ ra các khoảng đồng biến và nghịch biến của hàm số đã cho. Hoạt động khám phá 1 trang 7 Toán 12 Tập 1

Thực hành 2 trang 9 Toán 12 Tập 1
Xét tính đơn điệu của các hàm số sau. Thực hành 2 trang 9 Toán 12 Tập 1
Thực hành 3 trang 9 Toán 12 Tập 1
Chứng minh rằng hàm số f(x) = 3x – sinx đồng biến trên ℝ. Thực hành 3 trang 9 Toán 12 Tập 1

Vận dụng 1 trang 9 Toán 12 Tập 1
Hãy trả lời câu hỏi trong phần khởi động (trang 6) bằng cách xét dấu đạo hàm của hàm số h(t) = 6t3 – 81t2 + 324t với 0 ≤ t ≤ 8. Vận dụng 1 trang 9 Toán 12 Tập 1

Hoạt động khám phá 2 trang 10 Toán 12 Tập 1
Quan sát đồ thị của hàm số y = f(x) trong Hình 5. Tìm khoảng (a; b) chứa điểm x = 0 mà trên đó f(x) < f(0) với mọi x ≠ 0. Hoạt động khám phá 2 trang 10 Toán 12 Tập 1

Thực hành 4 trang 11 Toán 12 Tập 1
Tìm các điểm cực trị của hàm số y = f(x) có đồ thị cho ở Hình 8. Thực hành 4 trang 11 Toán 12 Tập 1
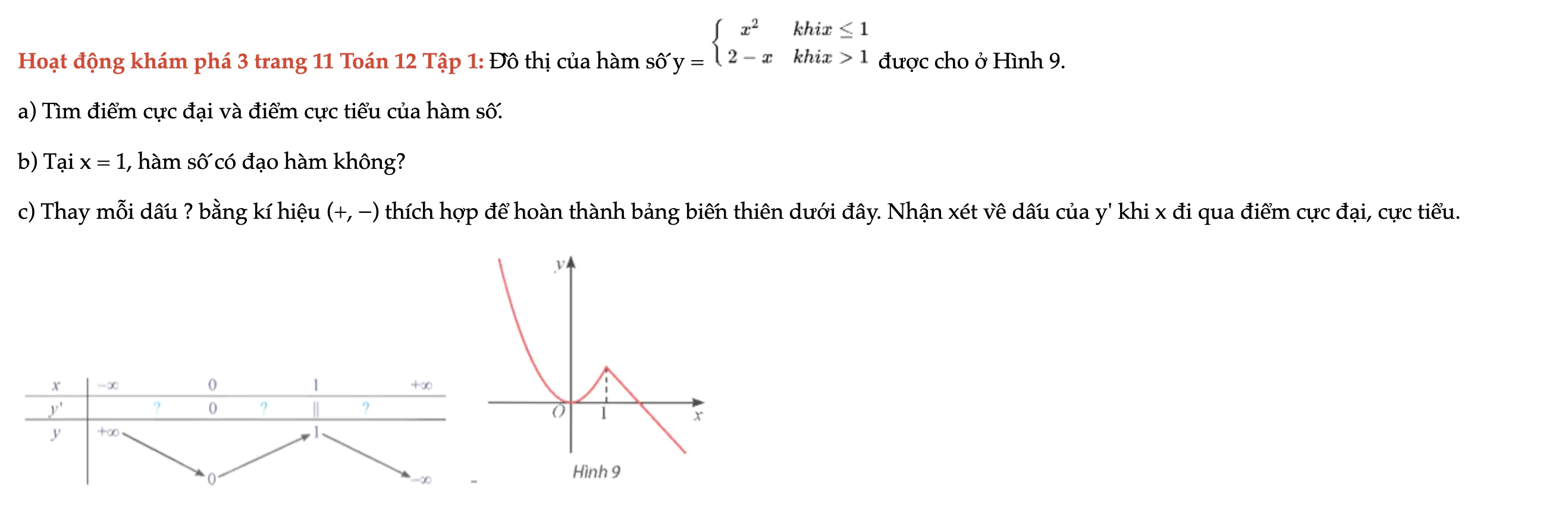
Hoạt động khám phá 3 trang 11 Toán 12 Tập 1
Đồ thị của hàm số y được cho ở Hình 9. Tìm điểm cực đại và điểm cực tiểu của hàm số. Hoạt động khám phá 3 trang 11 Toán 12 Tập 1
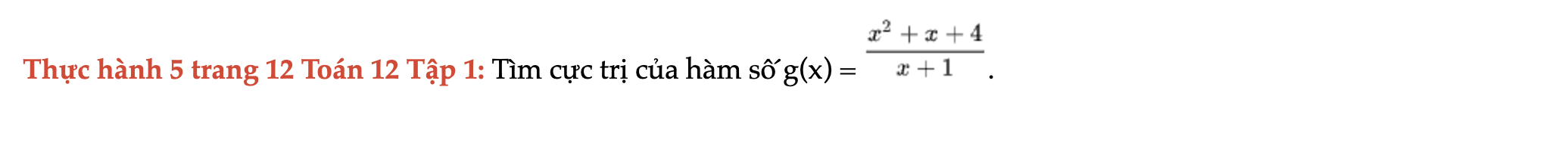
Thực hành 5 trang 12 Toán 12 Tập 1
Tìm cực trị của hàm số g(x). Thực hành 5 trang 12 Toán 12 Tập 1

Vận dụng 2 trang 12 Toán 12 Tập 1
Một phần lát cắt của dãy núi có độ cao tính bằng mét được mô tả bởi hàm số y = h(x). Tìm tọa độ các đỉnh của lát cắt dãy núi trên đọan [0; 2000]. Vận dụng 2 trang 12 Toán 12 Tập 1
Giải bài tập Bài 2. Giá trị lớn nhất, giá trị nhỏ nhất của hàm số.
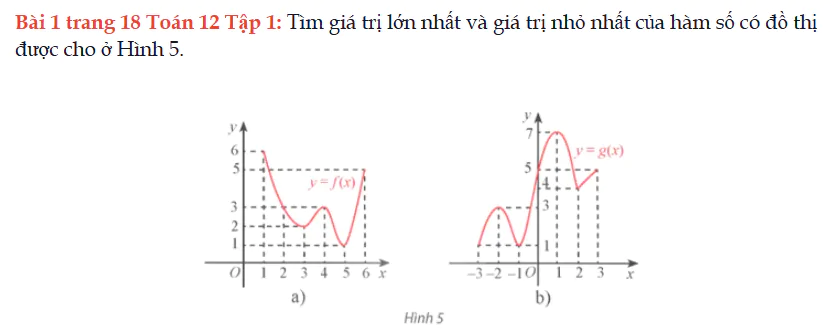
Bài 1 trang 18 Toán 12 Tập 1
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số có đồ thị được cho ở Hình 5. Bài 1 trang 18 Toán 12 Tập 1

Bài 2 trang 18 Toán 12 Tập 1
Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau. Bài 2 trang 18 Toán 12 Tập 1

Bài 3 trang 18 Toán 12 Tập 1
Tìm giá trị nhỏ nhất của các hàm số sau. Bài 3 trang 18 Toán 12 Tập 1

Bài 4 trang 18 Toán 12 Tập 1
Khi làm nhà kho, bác An muốn cửa số có dạng hình chữ nhật với chu vi bằng 4 m (Hình 6). Tìm kích thước khung cửa sổ sao cho diện tích cửa sổ lớn nhất (để hứng được nhiều ánh sáng nhất)? Bài 4 trang 18 Toán 12 Tập 1

Bài 5 trang 18 Toán 12 Tập 1
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số. Bài 5 trang 18 Toán 12 Tập 1

Bài 6 trang 18 Toán 12 Tập 1
Khối lượng q (kg) của một mặt hàng mà cửa tiệm bán được trong một ngày phụ thuộc vào giá bán p (nghìn đồng/kg) theo công thức. Bài 6 trang 18 Toán 12 Tập 1

Bài 7 trang 18 Toán 12 Tập 1
Hộp sữa 1 l được thiết kế dạng hình hộp chữ nhật với đáy là hình vuông cạnh x cm. Tìm x để diện tích toàn phần của hộp nhỏ nhất. Bài 7 trang 18 Toán 12 Tập 1

Hoạt động khởi động trang 14 Toán 12 Tập 1
Sự phân hủy của rác thải hữu cơ có trong nước sẽ làm tiêu hao oxygen hòa tan trong nước. Hoạt động khởi động trang 14 Toán 12 Tập 1

Hoạt động khám phá 1 trang 14 Toán 12 Tập 1
Hình 1 cho biết sự thay đổi của nhiệt độ ở một thành phố trong một ngày. Khẳng định nào sau đây đúng? Vì sao? Hoạt động khám phá 1 trang 14 Toán 12 Tập 1

Thực hành 1 trang 16 Toán 12 Tập 1
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số. Thực hành 1 trang 16 Toán 12 Tập 1

Vận dụng trang 16 Toán 12 Tập 1
Sử dụng đạo hàm và lập bảng biến thiên, trả lời câu hỏi trong mục khởi động (trang 14). Vận dụng trang 16 Toán 12 Tập 1
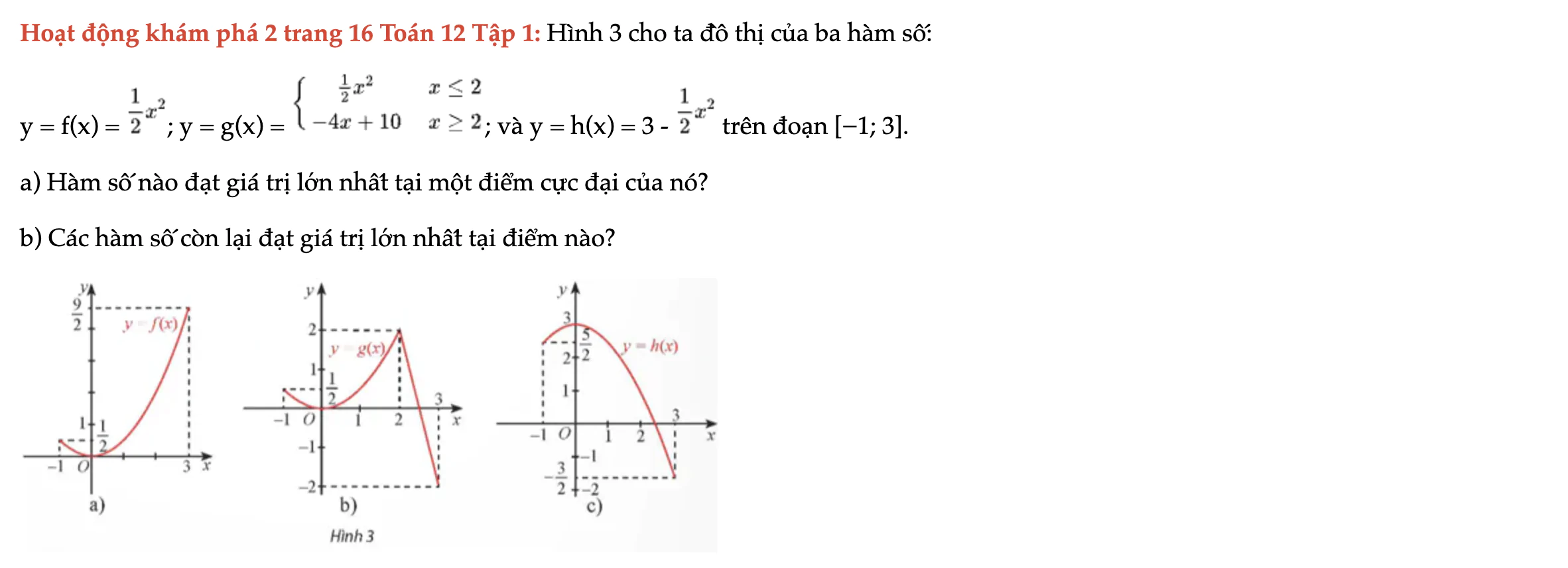
Hoạt động khám phá 2 trang 16 Toán 12 Tập 1
Hình 3 cho ta đồ thị của ba hàm số. Hàm số nào đạt giá trị lớn nhất tại một điểm cực đại của nó? Hoạt động khám phá 2 trang 16 Toán 12 Tập 1

Thực hành 2 trang 18 Toán 12 Tập 1
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số g(x) trên đoạn [1; 4]. Thực hành 2 trang 18 Toán 12 Tập 1
Thực hành 3 trang 18 Toán 12 Tập 1
Tam giác vuông có cạnh huyền bằng 5 cm có thể có diện tích lớn nhất bằng bao nhiêu? Thực hành 3 trang 18 Toán 12 Tập 1
Giải bài tập Bài 3. Đường tiệm cận của đồ thị hàm số.
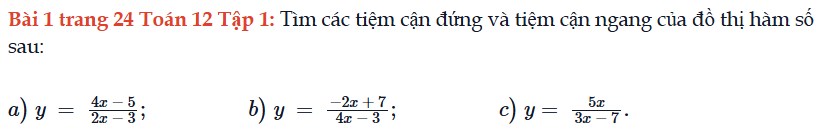
Bài 1 trang 24 Toán 12 Tập 1
Tìm các tiệm cận đứng và tiệm cận ngang của đồ thị hàm số sau. Bài 1 trang 24 Toán 12 Tập 1
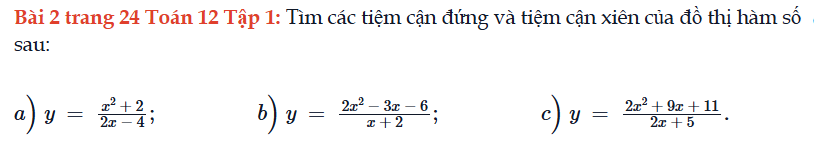
Bài 2 trang 24 Toán 12 Tập 1
Tìm các tiệm cận đứng và tiệm cận xiên của đồ thị hàm số sau. Bài 2 trang 24 Toán 12 Tập 1
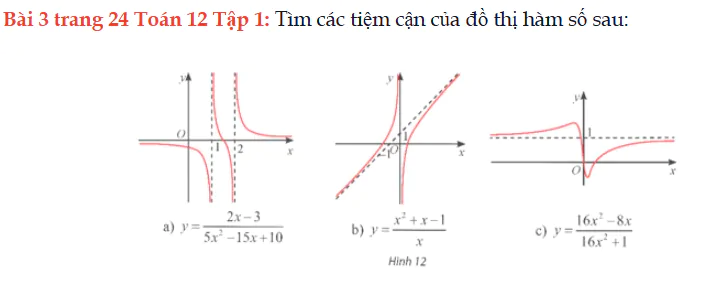
Bài 3 trang 24 Toán 12 Tập 1
Tìm các tiệm cận của đồ thị hàm số sau. Bài 3 trang 24 Toán 12 Tập 1
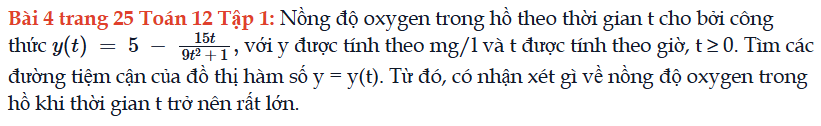
Bài 4 trang 25 Toán 12 Tập 1
Nồng độ oxygen trong hồ theo thời gian t cho bởi công thức, với y được tính theo mg/l và t được tính theo giờ. Bài 4 trang 25 Toán 12 Tập 1

Bài 5 trang 25 Toán 12 Tập 1
Tìm tiệm cận của đồ thị hàm số khối lượng hạt trong hoạt động khởi động (trang 19). Bài 5 trang 25 Toán 12 Tập 1

Hoạt động khởi động trang 19 Toán 12 Tập 1
Theo thuyết tương đối hẹp, khối lượng m (kg) của một hạt phụ thuộc vào tốc độ di chuyển v (km/s) của nó trong hệ quy chiếu quán tính, trong đó m0 là khối lượng nghỉ của hạt c = 300 000 km/s là tốc độ ánh sáng. Hoạt động khởi động trang 19 Toán 12 Tập 1

Hoạt động khám phá 1 trang 19 Toán 12 Tập 1
Cho hàm số y có đồ thị như Hình 1. Tính các giới hạn đã cho. Gọi M là điểm trên đồ thị có hoành độ x. Đường thẳng đi qua M và vuông góc với trục Oy cắt đường thẳng x = 1 tại điểm N. Hoạt động khám phá 1 trang 19 Toán 12 Tập 1

Thực hành 1 trang 20 Toán 12 Tập 1
Tìm tiệm cận đứng của đồ thị các hàm số sau. Thực hành 1 trang 20 Toán 12 Tập 1

Hoạt động khám phá 2 trang 21 Toán 12 Tập 1
Cho hàm số y có đồ thị như Hình 4. Tìm các giới hạn đã cho. Đường thẳng vuông góc với trục Ox tại điểm x cắt đồ thị hàm số tại điểm M và cắt đường thẳng y = 1 tại điểm N (Hình 4). Hoạt động khám phá 2 trang 21 Toán 12 Tập 1

Thực hành 2 trang 21 Toán 12 Tập 1
Tìm tiệm cận ngang của đồ thị các hàm số sau. Thực hành 2 trang 21 Toán 12 Tập 1

Hoạt động khám phá 3 trang 22 Toán 12 Tập 1
Cho đồ thị của hàm số y và đường thẳng y = x. Đường thẳng vuông góc với trục Ox tại điểm x cắt đồ thị hàm số tại điểm M và cắt đường thẳng y = x tại điểm N (Hình 7). Hoạt động khám phá 3 trang 22 Toán 12 Tập 1
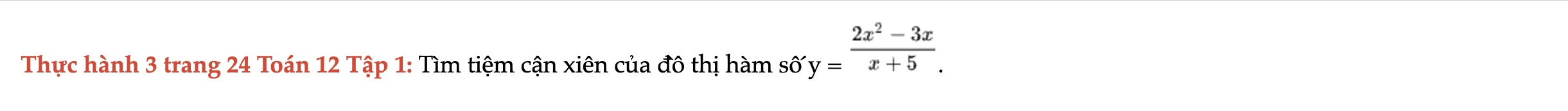
Thực hành 3 trang 24 Toán 12 Tập 1
Tìm tiệm cận xiên của đồ thị hàm số y. Thực hành 3 trang 24 Toán 12 Tập 1

Thực hành 4 trang 24 Toán 12 Tập 1
Nếu trong một ngày, một xưởng sản xuất được x kilôgam sản phẩm thì chi phí trung bình (tính bằng nghìn đồng) cho một sản phẩm. Tìm các đường tiệm cận của đồ thị hàm số y = C(x). Thực hành 4 trang 24 Toán 12 Tập 1
Giải bài tập Bài 4. Khảo sát và vẽ đồ thị một số hàm số cơ bản.

Bài 1 trang 36 Toán 12 Tập 1
Khảo sát và vẽ đồ thị của các hàm số sau. Bài 1 trang 36 Toán 12 Tập 1

Bài 2 trang 36 Toán 12 Tập 1
Chứng minh trung điểm của đoạn thẳng nối hai điểm cực trị của đồ thị hàm số có hoành độ là nghiệm của phương trình đạo hàm cấp 2. Bài 2 trang 36 Toán 12 Tập 1

Bài 3 trang 36 Toán 12 Tập 1
Khảo sát và vẽ đồ thị của các hàm số. Bài 3 trang 36 Toán 12 Tập 1

Bài 4 trang 36 Toán 12 Tập 1
Khảo sát và vẽ đồ thị của các hàm số. Bài 4 trang 36 Toán 12 Tập 1
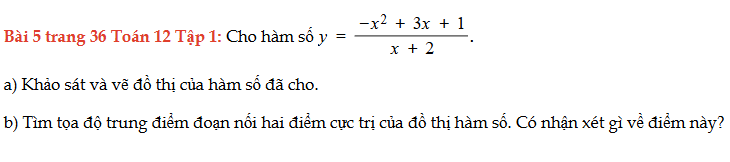
Bài 5 trang 36 Toán 12 Tập 1
Cho hàm số y = f(x), khảo sát và vẽ đồ thị của hàm số. Tìm tọa độ trung điểm nối hay điểm cực trị của đồ thị hàm số và nhận xét. Bài 5 trang 36 Toán 12 Tập 1

Bài 6 trang 36 Toán 12 Tập 1
Bạn Việt muốn dùng tấm bìa hình vuông cạnh 6 dm làm một chiếc hộp không nắp, có đáy là hình vuông bằng cách cắt bỏ đi 4 hình vuông nhỏ ở bốn góc của tấm bìa (Hình 11). Thiết lập hàm số, khảo sát và vẽ đồ thị hàm số. Bài 6 trang 36 Toán 12 Tập 1

Hoạt động khởi động trang 25 Toán 12 Tập 1
Giả sử chi phí tiền xăng C (đồng) phụ thuộc tốc độ trung bình v (km/h). Để biểu diễn trực quan sự thay đổi của C(v) theo v, người ta đã vẽ đồ thị hàm số C = C(v) như hình bên. Hoạt động khởi động trang 25 Toán 12 Tập 1
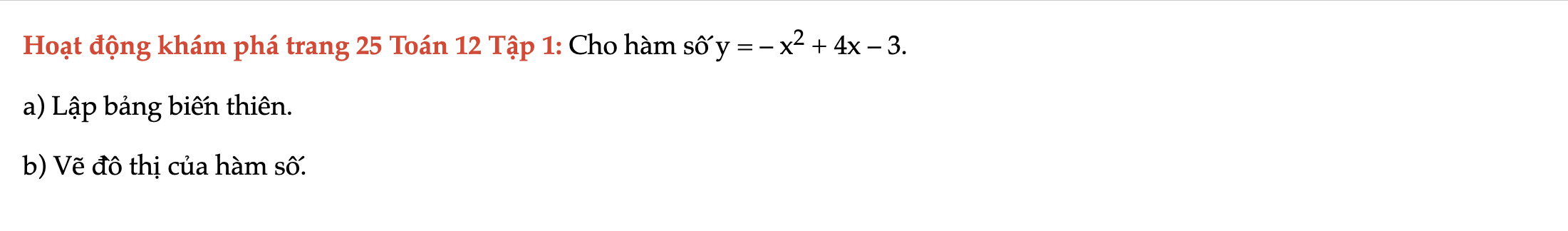
Hoạt động khám phá trang 25 Toán 12 Tập 1
Cho hàm số y = – x^2 + 4x – 3. Lập bảng biến thiên. Vẽ đồ thị của hàm số. Hoạt động khám phá trang 25 Toán 12 Tập 1

Thực hành 1 trang 28 Toán 12 Tập 1
Khảo sát và vẽ đồ thị của các hàm số sau. Thực hành 1 trang 28 Toán 12 Tập 1

Thực hành 2 trang 30 Toán 12 Tập 1
Khảo sát và vẽ đồ thị của các hàm số sau. Thực hành 2 trang 30 Toán 12 Tập 1

Thực hành 3 trang 32 Toán 12 Tập 1
Khảo sát và vẽ đồ thị của các hàm số sau. Thực hành 3 trang 32 Toán 12 Tập 1

Thực hành 4 trang 35 Toán 12 Tập 1
Xét một vật thật đặt trước thấu kính hội tụ có tiêu cự f > 0. Gọi d là khoảng cách từ vật đến thấu kính (d > 0), d' là khoảng cách từ thấu kính đến ảnh (ảnh thật thì d' > 0, ảnh ảo thì d' < 0). Thực hành 4 trang 35 Toán 12 Tập 1

Thực hành 5 trang 35 Toán 12 Tập 1
Người ta muốn chế tạo một chiếc hộp hình hộp chữ nhật có thể tích 500 cm3 với yêu cầu dùng ít vật liệu nhất. Thực hành 5 trang 35 Toán 12 Tập 1
Giải bài tập Bài tập cuối chương I.
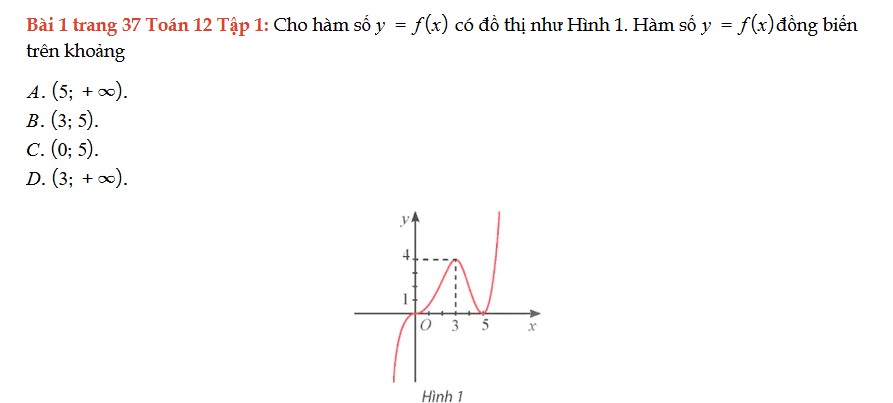
Bài 1 trang 37 Toán 12 Tập 1
Cho hàm số y = f(x) có đồ thị như Hình 1. Hàm số y = f(x) đồng biến trên khoảng. Bài 1 trang 37 Toán 12 Tập 1
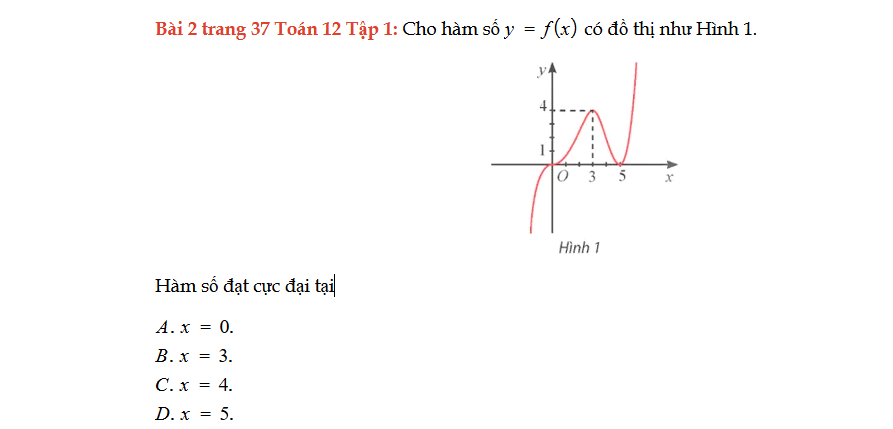
Bài 2 trang 37 Toán 12 Tập 1
Cho đồ thị hàm số y = f(x), hàm số đạt cực đại tại. Bài 2 trang 37 Toán 12 Tập 1

Bài 3 trang 37 Toán 12 Tập 1
Cho hàm số y = f(x), trong các khẳng định sau, khẳng định nào đúng? Bài 3 trang 37 Toán 12 Tập 1
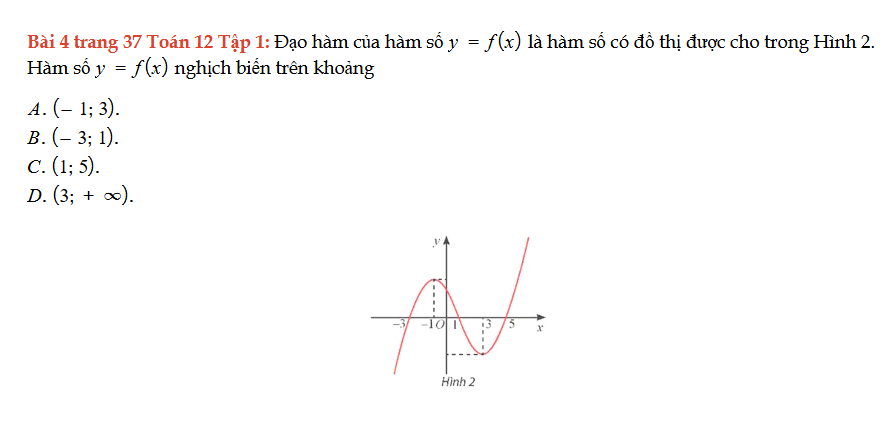
Bài 4 trang 37 Toán 12 Tập 1
Đạo hàm của hàm số y = f(x) là hàm số có đồ thị được cho trong Hình 2. Hàm số y = f(x) nghịch biến trên khoảng nào? Bài 4 trang 37 Toán 12 Tập 1
Bài 5 trang 37 Toán 12 Tập 1
Tìm giá trị nhỏ nhất của hàm số y = f(x) trên đoạn [-2; 3]. Bài 5 trang 37 Toán 12 Tập 1

Bài 6 trang 37 Toán 12 Tập 1
Tìm tiệm cận xiên của đồ thị hàm số y = f(x). Bài 6 trang 37 Toán 12 Tập 1

Bài 7 trang 37 Toán 12 Tập 1
Tìm tiệm cận đứng của đồ thị hàm số y = f(x). Bài 7 trang 37 Toán 12 Tập 1

Bài 8 trang 38 Toán 12 Tập 1
Cho hàm số y = f(x), hỏi khoảng đồng biến nghịch biến. Bài 8 trang 38 Toán 12 Tập 1

Bài 9 trang 38 Toán 12 Tập 1
Tìm hai số không âm a và b có tổng bằng 10 sao cho phù hợp với yêu cầu đề bài. Bài 9 trang 38 Toán 12 Tập 1
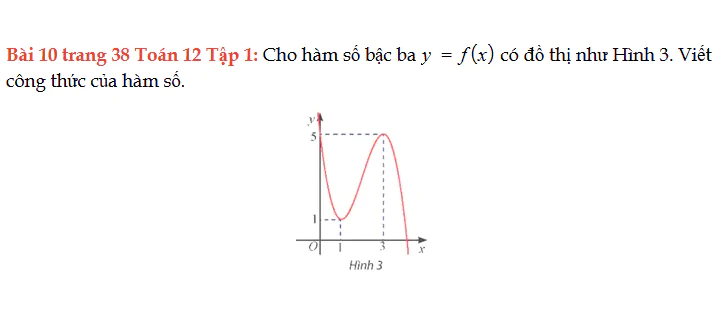
Bài 10 trang 38 Toán 12 Tập 1
Cho hàm số bậc ba y = f(x) có đồ thị như hình vẽ, viết công thức của hàm số. Bài 10 trang 38 Toán 12 Tập 1

Bài 11 trang 38 Toán 12 Tập 1
Cho hàm số y = f(x), khảo sát và vẽ đồ thị, tính khoảng cách giữa hai điểm cực trị. Bài 11 trang 38 Toán 12 Tập 1

Bài 12 trang 38 Toán 12 Tập 1
Cho hàm số y = f(x), khảo sát và vẽ đồ thị hàm số. Tìm điểm B đối xứng với A qua I. Chứng minh rằng điểm B cũng thuộc đồ thị hàm số này. Bài 12 trang 38 Toán 12 Tập 1

Bài 13 trang 38 Toán 12 Tập 1
Cho hàm số y = f(x), khảo sát và vẽ đồ thị hàm số. Tìm giá trị lớn nhất ( GTLN), giá trị nhỏ nhất (GTNN) theo yêu cầu đề bài. Bài 13 trang 38 Toán 12 Tập 1
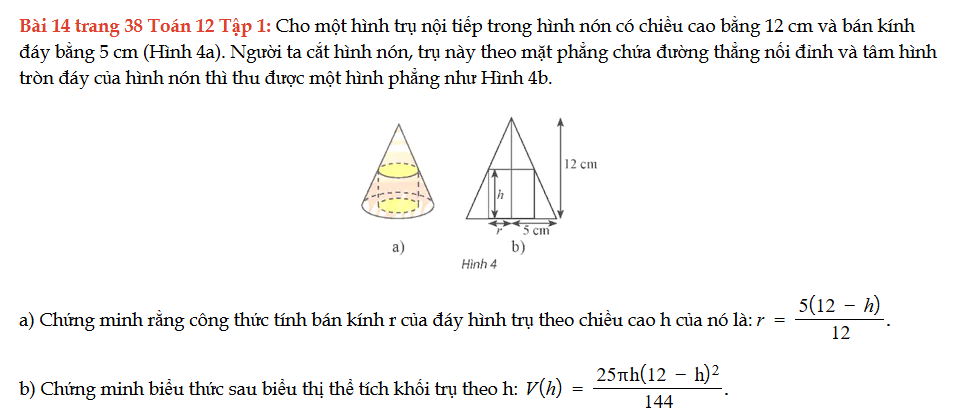
Bài 14 trang 38 Toán 12 Tập 1
Cho một hình trụ nội tiếp trong hình nón có các số đo như sau, chứng minh các biểu thức sau là đúng. Bài 14 trang 38 Toán 12 Tập 1

Bài 15 trang 39 Toán 12 Tập 1
Trong một nhà hàng, mỗi tuần để chế biến x phần ăn (x lấy giá trị trong khoảng từ 30 đến 120) thì chi phí trung bình (đơn vị: nghìn đồng) của một phần ăn được cho bởi công thức sau. Thực hiện các yêu cầu đề bài. Bài 15 trang 39 Toán 12 Tập 1
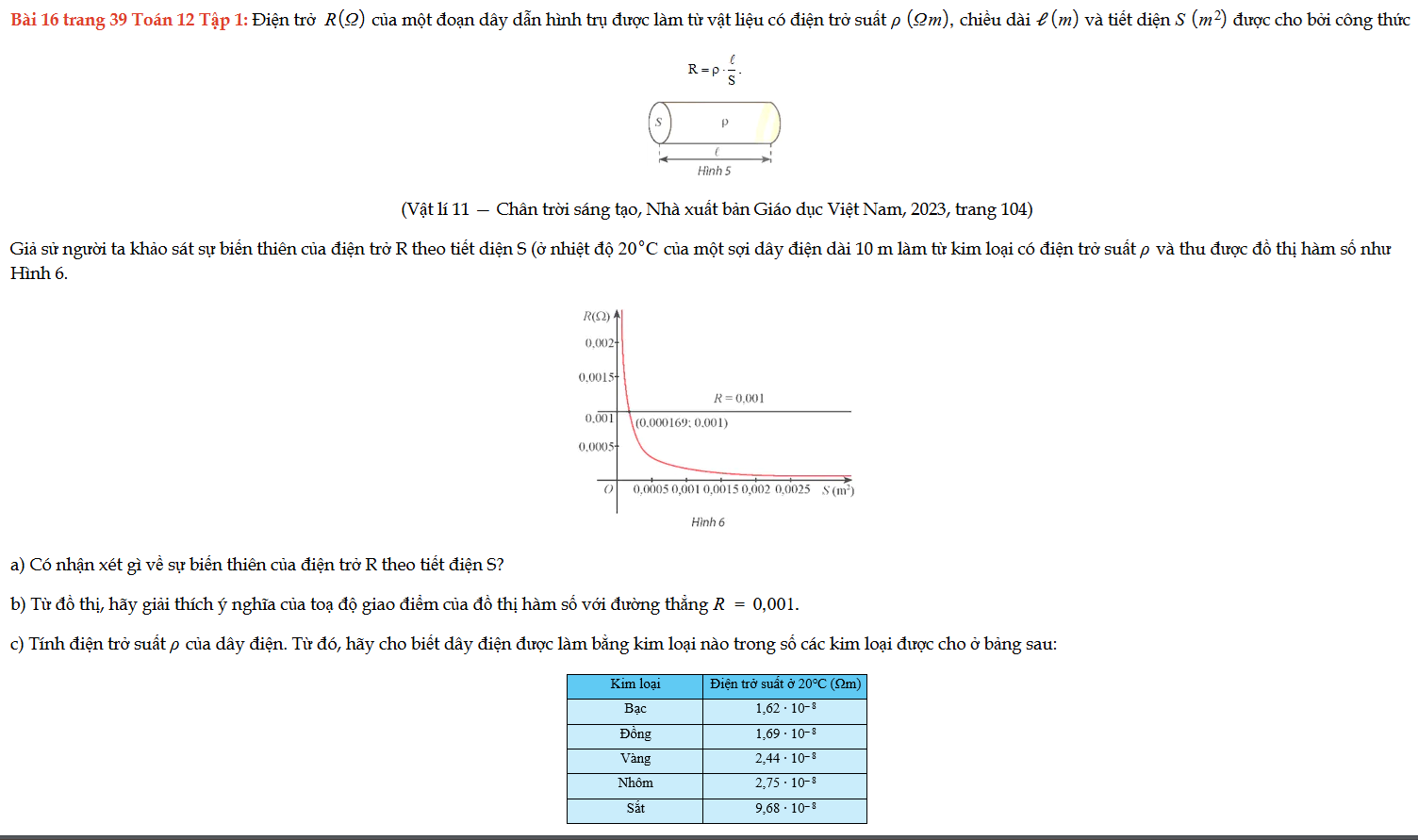
Bài 16 trang 39 Toán 12 Tập 1
Điện trở của một đoạn dây dẫn hình trụ được làm từ vật liệu có điện trở suất, chiều dài và tiết diện được cho bởi công thức sau, thực hiện các yêu cầu đề bài. Bài 16 trang 39 Toán 12 Tập 1