Giải bài tập Bài 2 trang 24 Toán 12 Tập 1 | SGK Toán 12 - Chân trời sáng tạo

Hướng dẫn giải chi tiết từng bước bài tập Bài 2 trang 24 Toán 12 Tập 1. Bài 3. Đường tiệm cận của đồ thị hàm số.. SGK Toán 12 - Chân trời sáng tạo

Đề bài:

Bài 2 trang 24 Toán 12 Tập 1: Tìm các tiệm cận đứng và tiệm cận xiên của đồ thị hàm số sau:

$a) y = \frac{x^{2} + 2}{2 x - 4}; b) y = \frac{2 x^{2} - 3 x - 6}{x + 2}; c) y = \frac{2 x^{2} + 9 x + 11}{2 x + 5} .$

Đáp án và cách giải chi tiết:

a) Tập xác định: $D = ℝ \ \{- 2\} .$

Có $\underset{x \to 2^{+}}{l i m} y = \underset{x \to 2^{+}}{l i m} \frac{x^{2} + 2}{2 x - 4} = + \infty; \underset{x \to 2^{-}}{l i m} y = \underset{x \to 2^{-}}{l i m} \frac{x^{2} + 2}{2 x - 4} = - \infty .$

Vậy x = 2 là tiệm cận đứng của đồ thị hàm số.

Có $y = \frac{x^{2} + 2}{2 x - 4} = \frac{1}{2} x + 1 + \frac{6}{2 x - 4} .$

Có

$\underset{x \to + \infty}{l i m} [y - (\frac{1}{2} x + 1)] = \underset{x \to + \infty}{l i m} [\frac{1}{2} x + 1 + \frac{6}{2 x - 4} - (\frac{1}{2} x + 1)] = \underset{x \to + \infty}{l i m} \frac{6}{2 x - 4} = 0 . \underset{x \to - \infty}{l i m} [y - (\frac{1}{2} x + 1)] = \underset{x \to - \infty}{l i m} [\frac{1}{2} x + 1 + \frac{6}{2 x - 4} - (\frac{1}{2} x + 1)] = \underset{x \to - \infty}{l i m} \frac{6}{2 x - 4} = 0 .$

Vậy $y = \frac{1}{2} x + 1$ là tiệm cận xiên của đồ thị hàm số.

b) Tập xác định: $D = ℝ \ \{- 2\} .$

$\underset{x \to {(- 2)}^{+}}{l i m} y = \underset{x \to {(- 2)}^{+}}{l i m} \frac{2 x^{2} - 3 x - 6}{x + 2} = + \infty; \underset{x \to {(- 2)}^{-}}{l i m} y = \underset{x \to {(- 2)}^{-}}{l i m} \frac{2 x^{2} - 3 x - 6}{x + 2} = - \infty$

Vậy x = −2 là tiệm cận đứng của đồ thị hàm số.

Có $y = \frac{2 x^{2} - 3 x - 6}{x + 2} = 2 x - 7 + \frac{8}{x + 2} .$

Có

$\underset{x \to + \infty}{l i m} [y - (2 x - 7)] = \underset{x \to + \infty}{l i m} [2 x - 7 + \frac{8}{x + 2} - (2 x - 7)] = \underset{x \to + \infty}{l i m} \frac{8}{x + 2} = 0; \underset{x \to - \infty}{l i m} [y - (2 x - 7)] = \underset{x \to - \infty}{l i m} [2 x - 7 + \frac{8}{x + 2} - (2 x - 7)] = \underset{x \to - \infty}{l i m} \frac{8}{x + 2} = 0$

Vậy y = 2x – 7 là tiệm cận xiên của đồ thị hàm số.

c) Tập xác định: $D = ℝ \ \{- \frac{5}{2}\} .$

$\underset{x \to {(- \frac{5}{2})}^{+}}{l i m} y = \underset{x \to {(- \frac{5}{2})}^{+}}{l i m} \frac{2 x^{2} + 9 x + 11}{2 x + 5} = + \infty; \underset{x \to {(- \frac{5}{2})}^{-}}{l i m} y = \underset{x \to {(- \frac{5}{2})}^{-}}{l i m} \frac{2 x^{2} + 9 x + 11}{2 x + 5} = - \infty$

Vậy là tiệm cận đứng của đồ thị hàm số.

Có $y = \frac{2 x^{2} + 9 x + 11}{2 x + 5} = x + 2 + \frac{1}{2 x + 5} .$

Có

$\underset{x \to + \infty}{l i m} [y - (x + 2)] = \underset{x \to + \infty}{l i m} [x + 2 + \frac{1}{2 x + 5} - (x + 2)] = \underset{x \to + \infty}{l i m} \frac{1}{2 x + 5} = 0; \underset{x \to - \infty}{l i m} [y - (x + 2)] = \underset{x \to - \infty}{l i m} [x + 2 + \frac{1}{2 x + 5} - (x + 2)] = \underset{x \to - \infty}{l i m} \frac{1}{2 x + 5} = 0;$

Vậy y = x + 2 là tiệm cận xiên của đồ thị hàm số.

Nguồn: loigiaitoan.com

Tổng số đánh giá:

Xếp hạng: / 5 sao

Bài tập liên quan:

Bài 1 trang 24 Toán 12 Tập 1

Bài 1 trang 24 Toán 12 Tập 1: Tìm các tiệm cận đứng và tiệm cận ngang của đồ thị hàm số sau:

$a) y = \frac{4 x - 5}{2 x - 3}; b) y = \frac{- 2 x + 7}{4 x - 3}; c) y = \frac{5 x}{3 x - 7} .$

Xem cách giải chi tiết

Bài 3 trang 24 Toán 12 Tập 1

Bài 3 trang 24 Toán 12 Tập 1: Tìm các tiệm cận của đồ thị hàm số sau:

Xem cách giải chi tiết

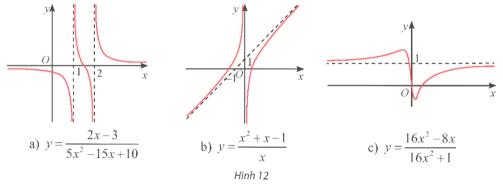
Bài 4 trang 25 Toán 12 Tập 1

Bài 4 trang 25 Toán 12 Tập 1: Nồng độ oxygen trong hồ theo thời gian t cho bởi công thức $y (t) = 5 - \frac{15 t}{9 t^{2} + 1},$ với y được tính theo mg/l và t được tính theo giờ, t ≥ 0. Tìm các đường tiệm cận của đồ thị hàm số y = y(t). Từ đó, có nhận xét gì về nồng độ oxygen trong hồ khi thời gian t trở nên rất lớn.

Xem cách giải chi tiết

Bài 5 trang 25 Toán 12 Tập 1

Bài 5 trang 25 Toán 12 Tập 1: Tìm tiệm cận của đồ thị hàm số khối lượng hạt $m = m (v) = \frac{m_{0}}{\sqrt{1 - \frac{v^{2}}{c^{2}}}}$ trong hoạt động khởi động (trang 19).

Xem cách giải chi tiết

Hoạt động khởi động trang 19 Toán 12 Tập 1

Theo thuyết tương đối hẹp, khối lượng m (kg) của một hạt phụ thuộc vào tốc độ di chuyển v (km/s) của nó trong hệ quy chiếu quán tính theo công thức m = m(v) = , trong đó m0 là khối lượng nghỉ của hạt c = 300 000 km/s là tốc độ ánh sáng. Khi hạt di chuyển với tốc độ càng gần tốc độ ánh sáng thì khối lượng của hạt thay đổi như thế nào? Điều này thể hiện trên đồ thị hàm số m = m(v) ở hình bên như thế nào?

Xem cách giải chi tiết

Hoạt động khám phá 1 trang 19 Toán 12 Tập 1

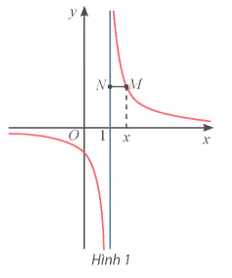
Cho hàm số y = có đồ thị như Hình 1.

a) Tính .

b) Gọi M là điểm trên đồ thị có hoành độ x. Đường thẳng đi qua M và vuông góc với trục Oy cắt đường thẳng x = 1 tại điểm N. Tính MN theo x và nhận xét về MN khi x → 1⁺; x → 1⁻.

Xem cách giải chi tiết

Thực hành 1 trang 20 Toán 12 Tập 1

Tìm tiệm cận đứng của đồ thị các hàm số sau:

a) y = f(x) = ;

b) y = g(x) = .

Xem cách giải chi tiết

Hoạt động khám phá 2 trang 21 Toán 12 Tập 1

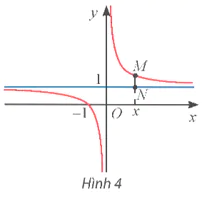
Cho hàm số y = 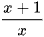có đồ thị như Hình 4.

a) Tìm .

b) Đường thẳng vuông góc với trục Ox tại điểm x cắt đồ thị hàm số tại điểm M và cắt đường thẳng y = 1 tại điểm N (Hình 4). Tính MN theo x và nhận xét về MN khi x → +∞ hoặc x → −∞.

Xem cách giải chi tiết

Thực hành 2 trang 21 Toán 12 Tập 1

Tìm tiệm cận ngang của đồ thị các hàm số sau:

a) y = f(x) = ;

b) y = g(x) = .

Xem cách giải chi tiết

Hoạt động khám phá 3 trang 22 Toán 12 Tập 1

Cho đồ thị của hàm số y = 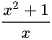và đường thẳng y = x. Đường thẳng vuông góc với trục Ox tại điểm x cắt đồ thị hàm số tại điểm M và cắt đường thẳng y = x tại điểm N (Hình 7).

a) Tính và ;

b) Tính MN theo x và nhận xét về MN khi x → +∞ hoặc x → −∞.

Xem cách giải chi tiết

Thực hành 3 trang 24 Toán 12 Tập 1

Tìm tiệm cận xiên của đồ thị hàm số y = .

Xem cách giải chi tiết

Thực hành 4 trang 24 Toán 12 Tập 1

Nếu trong một ngày, một xưởng sản xuất được x kilôgam sản phẩm thì chi phí trung bình (tính bằng nghìn đồng) cho một sản phẩm được cho bởi công thức: C(x) = . Tìm các đường tiệm cận của đồ thị hàm số y = C(x).

Xem cách giải chi tiết

Từ điển Phương Trình Hoá Học

BaCl2+K2CrO4 → KCl+BaCrO4 CaF2+H2SO4+SiO2 → H2O+CaSO4+SiF4 O2+Na2B4O7 → NaBO2+B2O3 Fe+H2O2 → Fe(OH)3 H2O2+NH4OH+As2S3 → (NH4)2SO4+H2O+(NH4)3AsO4

Công Thức Vật Lý

Góc chiết quang. Công thức Einstein. Năng lượng, công thoát và động năng cực đại trọng lượng tử năng lượng. Chuyển động của điện tích lệch góc với cảm ứng từ trong từ trường đều

Giải bài tập Bài 2 trang 24 Toán 12 Tập 1 | SGK Toán 12 - Chân trời sáng tạo

Đề bài:

Đáp án và cách giải chi tiết:

Bài tập liên quan:

Giải bài tập SGK Toán 12 - Chân trời sáng tạo

Chương 1. Ứng dụng đạo hàm để khảo sát hàm số

Bài 1. Tính đơn điệu và cực trị của hàm số.

Bài 2. Giá trị lớn nhất, giá trị nhỏ nhất của hàm số.

Bài 3. Đường tiệm cận của đồ thị hàm số.

Bài 4. Khảo sát và vẽ đồ thị một số hàm số cơ bản.

Bài tập cuối chương I.

Chương 2. Vectơ và hệ tọa độ trong không gian

Bài 1. Vectơ và các phép toán trong không gian.

Bài 2. Toạ độ của vectơ trong không gian.

Bài 3. Biểu thức toạ độ của các phép toán vectơ.

Bài tập cuối chương 2.

Chương 3. Các số đặc trưng đo mức độ phân tán cho mẫu số liệu ghép nhóm

Bài 1. Khoảng biến thiên và khoảng tứ phân vị của mẫu số liệu ghép nhóm.

Bài 2. Phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm.

Bài tập cuối chương 3.

Hoạt động thực hành và trải nghiệm

Bài 1. Vẽ đồ thị hàm số bằng phần mềm Geogebra 87.

Bài 2. Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số bằng máy tính cầm tay 91.

Chương 4. Nguyên hàm. Tích phân.

Bài 1. Nguyên hàm.

Bài 2. Tích phân.

Bài 3. Ứng dụng hình học của tích phân.

Bài tập cuối chương 4.

Chương 5. Phương trình mặt phẳng, đường thẳng, mặt cầu

Bài 1. Phương trình mặt phẳng

Bài 2. Phương trình đường thẳng trong không gian

Bài 3. Phương trình mặt cầu

Bài tập cuối chương 5

Chương 6. Xác suất có điều kiện

Bài 1. Xác suất có điều kiện

Bài 2. Công thức xác suất toàn phần và công thức Bayes.

Bài tập cuối chương 6

Hoạt động thực hành và trải nghiệm

Bài 1. Tính giá trị gần đúng tích phân bằng máy tính cầm tay.

Bài 2. Minh hoạ và tính tích phân bằng phần mềm GeoGebra.

Bài 3. Sử dụng phần mềm GeoGebra để biểu diễn hình học toạ độ trong không gian.

Từ điển Phương Trình Hoá Học

Công Thức Vật Lý