Giải bài tập Toán 12 Bài 1. Nguyên hàm. | Chân trời sáng tạo
Hướng dẫn giải chi tiết Bài 1. Nguyên hàm. Khái niệm Nguyên hàm, Nguyên hàm của hàm lũy thừa, phân thức, lượng giác, hàm mũ. Tính chất cơ bản của Nguyên hàm.
Bài 1 trang 11 Toán 12 Tập 2
Bài 1 trang 11 Toán 12 Tập 2: Tính đạo hàm của hàm số  , suy ra nguyên hàm của hàm số
, suy ra nguyên hàm của hàm số  .
.
Bài 2 trang 11 Toán 12 Tập 2
Bài 2 trang 11 Toán 12 Tập 2: Tìm:
a) 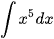 ; b)
; b)  ; c)
; c) 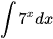 ; d)
; d) 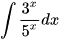 .
.
Bài 3 trang 11 Toán 12 Tập 2
Bài 3 trang 11 Toán 12 Tập 2: Tìm nguyên hàm  của hàm số
của hàm số 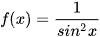 thỏa mãn
thỏa mãn 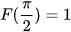 .
.
Bài 4 trang 11 Toán 12 Tập 2
Bài 4 trang 11 Toán 12 Tập 2: Tìm:
a) 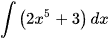 ; b)
; b) 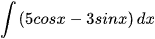 ;
;
c) 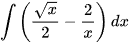 ; d)
; d) 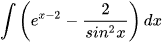 .
.
Bài 5 trang 12 Toán 12 Tập 2
Bài 5 trang 12 Toán 12 Tập 2: Tìm:
a)  ; b)
; b)  ;
;
c)  ; c)
; c)  .
.
Bài 6 trang 12 Toán 12 Tập 2
Bài 6 trang 12 Toán 12 Tập 2: Kí hiệu h(x) là chiều cao của một cây (tính theo mét) sau khi trồng x năm. Biết rằng sau năm đầu tiên cây cao 2 m. Trong 10 năm tiếp theo, cây phát triển với tốc độ 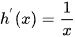 (m/năm).
(m/năm).
a) Xác định chiều cao của cây sau x năm  .
.
b) Sau bao nhiêu năm cây cao 3 m?
Bài 7 trang 12 Toán 12 Tập 2
Bài 7 trang 12 Toán 12 Tập 2: Một chiếc xe đang chuyển động với vận tốc  thì tăng tốc với gia tốc không đổi
thì tăng tốc với gia tốc không đổi  . Tính quãng đường xe đó đi được trong 3 giây kể từ khi bắt đầu tăng tốc.
. Tính quãng đường xe đó đi được trong 3 giây kể từ khi bắt đầu tăng tốc.
Hoạt động khởi động trang 6 Toán 12 Tập 2
Khi được thả từ độ cao 20 m, một vật rơi với gia tốc không đổi a = 10 m/s2. Sau khi rơi được t giây thì vật có tốc độ bao nhiêu và đi được quãng đường bao nhiêu?
Hoạt động khám phá 1 trang 6 Toán 12 Tập 2
Cho hàm số f(x) = 2x xác định trên ℝ. Tìm một hàm số F(x) sao cho F'(x) = f(x).
Hoạt động khám phá 2 trang 6 Toán 12 Tập 2
Cho hàm số f(x) = 3x2 xác định trên ℝ.
a) Chứng minh rằng F(x) = x3 là một nguyên hàm của f(x) trên ℝ.
b) Với C là hằng số tùy ý, hàm số H(x) = F(x) + C có là nguyên hàm của f(x) trên ℝ không?
c) Giả sử G(x) là một nguyên hàm của f(x) trên ℝ. Tìm đạo hàm của hàm số G(x) – F(x). Từ đó, có nhận xét gì về hàm số G(x) – F(x)?
Thực hành 1 trang 7 Toán 12 Tập 2
Chứng minh rằng F(x) = e2x + 1 là một nguyên hàm của hàm số f(x) = 2e2x + 1 trên ℝ.
Hoạt động khám phá 3 trang 8 Toán 12 Tập 2
a) Giải thích tại sao 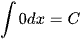 và
và 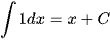 .
.
b) Tìm đạo hàm của hàm số 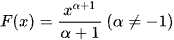 . Từ đó, tìm
. Từ đó, tìm  .
.
Hoạt động khám phá 4 trang 8 Toán 12 Tập 2
Cho hàm số F(x) = ln|x| với x ≠ 0.
a) Tìm đạo hàm của F(x).
b) Từ đó, tìm  .
.
Hoạt động khám phá 5 trang 9 Toán 12 Tập 2
a) Tìm đạo hàm của các hàm số y = sinx, y = −cosx, y = tanx, y = −cotx.
b) Từ đó, tìm 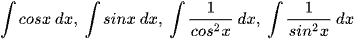 .
.
Thực hành 3 trang 9 Toán 12 Tập 2
Tìm nguyên hàm F(x) của hàm số f(x) = cosx thỏa mãn 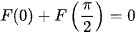 .
.
Hoạt động khám phá 6 trang 9 Toán 12 Tập 2
a) Tìm đạo hàm của các hàm số y = ex, 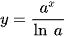 với a > 0, a ≠ 1.
với a > 0, a ≠ 1.
b) Từ đó, tìm 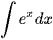 và
và  (a > 0, a ≠ 1).
(a > 0, a ≠ 1).
Hoạt động khám phá 7 trang 10 Toán 12 Tập 2
Ta có 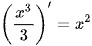 và (x3)' = 3x2.
và (x3)' = 3x2.
a) Tìm 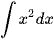 và 3
và 3 .
.
b) Tìm  .
.
c) Từ các kết quả trên, giải thích tại sao  .
.
Hoạt động khám phá 8 trang 10 Toán 12 Tập 2
Ta có 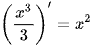 , (x2)' = 2x và
, (x2)' = 2x và 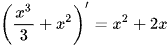 .
.
a) Tìm  và
và 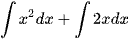 .
.
b) Tìm  .
.
c) Từ các kết quả trên, giải thích tại sao  .
.
Thực hành 7 trang 11 Toán 12 Tập 2
Một ô tô đang chạy với tốc độ 19 m/s thì hãm phanh và chuyển động chậm dần với tốc độ v(t) = 19 – 2t (m/s). Kể từ khi hãm phanh, quãng đường ô tô đi được sau 1 giây, 2 giây, 3 giây là bao nhiêu?
 ;
; ;
; (x > 0).
(x > 0). ;
;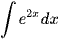 .
.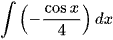 ;
;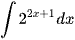 .
.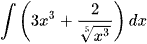 (x > 0);
(x > 0);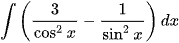 .
.