Giải bài tập Toán 12 Chương 5. Phương trình mặt phẳng, đường thẳng, mặt cầu | Chân trời sáng tạo
Chương V. Phương trình mặt phẳng, đường thẳng, mặt cầu. Tìm hiểu về Phương trình mặt phẳng, đường thẳng, mặt cầu trong không gian Oxyz và cách vận dụng để giải quyết vấn đề trong thực tiễn.
Giải bài tập Bài 1. Phương trình mặt phẳng

Bài 1 trang 42 Toán 12 Tập 2
Viết phương trình của các mặt phẳng sau. Bài 1 trang 42 Toán 12 Tập 2

Bài 2 trang 42 Toán 12 Tập 2
Lập phương trình của các mặt phẳng sau. Bài 2 trang 42 Toán 12 Tập 2

Bài 3 trang 42 Toán 12 Tập 2
Cho tứ diện ABCD có tọa độ các đỉnh, thực hiện các yêu cầu đề bài. Bài 3 trang 42 Toán 12 Tập 2

Bài 4 trang 42 Toán 12 Tập 2
Viết phương trình mặt phẳng (Q) đi qua C và song song với mặt phẳng (P). Bài 4 trang 42 Toán 12 Tập 2
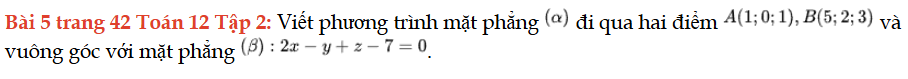
Bài 5 trang 42 Toán 12 Tập 2
Viết phương trình mặt phẳng đi qua hai điểm A, B và vuông góc với mặt phẳng. Bài 5 trang 42 Toán 12 Tập 2
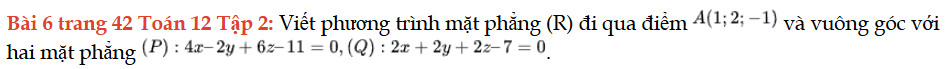
Bài 6 trang 42 Toán 12 Tập 2
Viết phương trình mặt phẳng (R) đi qua điểm A và vuông góc với hai mặt phẳng (P), (Q). Bài 6 trang 42 Toán 12 Tập 2
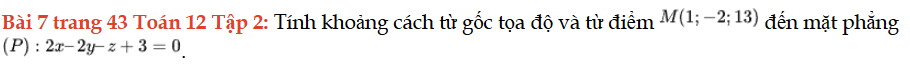
Bài 7 trang 43 Toán 12 Tập 2
Tính khoảng cách từ gốc tọa độ và từ điểm M đến mặt phẳng (P). Bài 7 trang 43 Toán 12 Tập 2
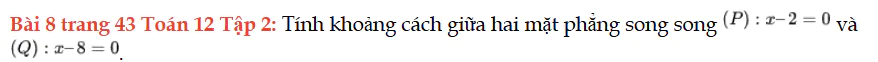
Bài 8 trang 43 Toán 12 Tập 2
Tính khoảng cách giữa hai mặt phẳng song song (P) và (Q).
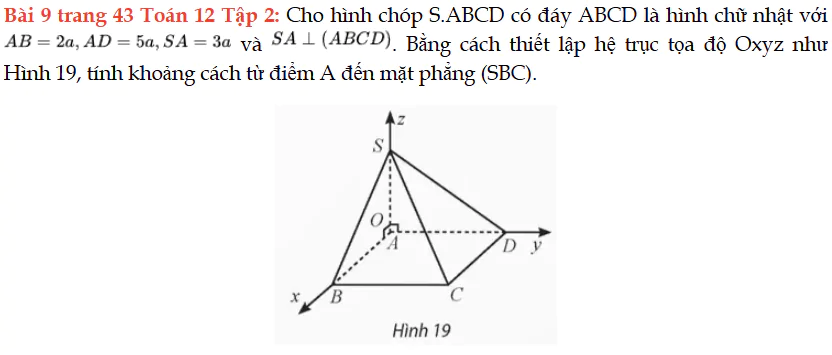
Bài 9 trang 43 Toán 12 Tập 2
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = 2a, AD = 5a, SA = 3a và SA vuông góc (ABCD), tính khoảng cách từ điểm A đến mặt phẳng (SBC). Bài 9 trang 43 Toán 12 Tập 2
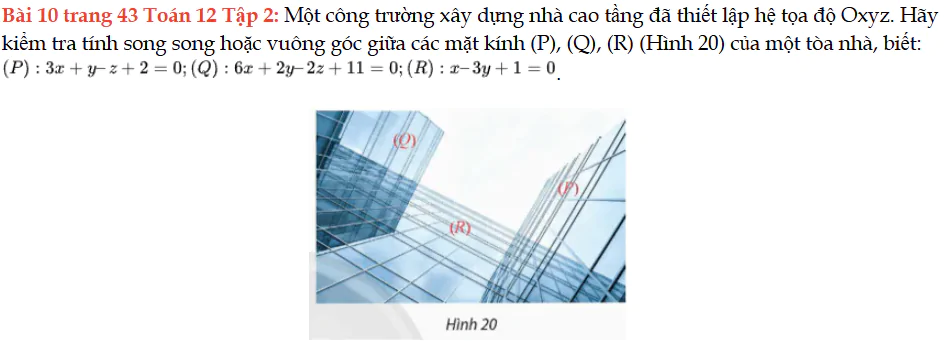
Bài 10 trang 43 Toán 12 Tập 2
Một công trường xây dựng nhà cao tầng đã thiết lập hệ tọa độ Oxyz. Hãy kiểm tra tính song song hoặc vuông góc giữa các mặt kính (P), (Q), (R) (Hình 20) của một tòa nhà. Bài 10 trang 43 Toán 12 Tập 2
Hoạt động khởi động trang 32 Toán 12 Tập 2
Trong không gian Oxyz, làm thế nào để xác định một mặt phẳng bằng phương pháp tọa độ? Hoạt động khởi động trang 32 Toán 12 Tập 2

Hoạt động khám phá 1 trang 32 Toán 12 Tập 2
Hoạt động khám phá 1 trang 32 Toán 12 Tập 2

Thực hành 1 trang 33 Toán 12 Tập 2
Trong không gian Oxyz, cho ba điểm A(3; 0; 0), B(0; 4; 0), C(0; 0; 5). Tìm tọa độ của một cặp vectơ chỉ phương của mặt phẳng (ABC). Tìm tọa độ của một vectơ pháp tuyến của mặt phẳng (OAB). Thực hành 1 trang 33 Toán 12 Tập 2

Vận dụng 1 trang 33 Toán 12 Tập 2
Một lăng kính có dạng hình lăng trụ đứng có đáy là tam giác đều ở Hình 3a được vẽ lại như Hình 3b. Tìm một cặp vectơ chỉ phương và một vectơ pháp tuyến của mặt phẳng (A'B'C'). Vận dụng 1 trang 33 Toán 12 Tập 2

Hoạt động khám phá 2 trang 33 Toán 12 Tập 2
Hoạt động khám phá 2 trang 33 Toán 12 Tập 2
Thực hành 2 trang 34 Toán 12 Tập 2
Cho mặt phẳng (Q) đi qua ba điểm A(1; 1; 1), B(−1; 1; 5), C(10; 7; −1). Tìm cặp vectơ chỉ phương và một vectơ pháp tuyến của (Q). Thực hành 2 trang 34 Toán 12 Tập 2

Vận dụng 2 trang 34 Toán 12 Tập 2
Cho biết hai vectơ a = (2; 1; 1), b = (1; -2; 0) có giá lần lượt song song với ngón trỏ và ngón giữa của bàn tay trong Hình 5. Tìm vectơ n có giá song song với ngón cái. Vận dụng 2 trang 34 Toán 12 Tập 2

Hoạt động khám phá 3 trang 35 Toán 12 Tập 2
Hoạt động khám phá 3 trang 35 Toán 12 Tập 2

Thực hành 3 trang 36 Toán 12 Tập 2
Cho hai mặt phẳng (α), (β) có phương trình tổng quát là (α): 2x + 2y – 3z – 4 = 0 và (β): x + 4z – 12 = 0. Tìm một vectơ pháp tuyến của mỗi mặt phẳng (α), (β). Thực hành 3 trang 36 Toán 12 Tập 2

Hoạt động khám phá 4 trang 36 Toán 12 Tập 2
Trong không gian Oxyz, cho mặt phẳng (α) đi qua điểm M0(x0; y0; z0) và nhận vectơ n = (A; B; C) làm vectơ pháp tuyến. Gọi M(x; y; z) là một điểm tùy ý trong không gian. Hoạt động khám phá 4 trang 36 Toán 12 Tập 2

Hoạt động khám phá 5 trang 36 Toán 12 Tập 2
Trong không gian Oxyz, cho mặt phẳng (α) đi qua điểm M(0; 2; 1) và có cặp vectơ chỉ phương là vectơ a = (1; 3; 1), vectơ b = (2; 0; 1). Tìm tọa độ một vectơ pháp tuyến của mặt phẳng (α). Hoạt động khám phá 5 trang 36 Toán 12 Tập 2

Hoạt động khám phá 6 trang 37 Toán 12 Tập 2
Trong không gian Oxyz, cho mặt phẳng (α) đi qua ba điểm A(0; 1; 1), B(2; 4; 3), C(5; 3; 1). Tìm tọa độ một cặp vectơ chỉ phương của mặt phẳng (α). Hoạt động khám phá 6 trang 37 Toán 12 Tập 2

Thực hành 4 trang 38 Toán 12 Tập 2
Viết phương trình mặt phẳng (P) trong mỗi trường hợp sau. (P) đi qua điểm A(2; 0; −1) và có vectơ pháp tuyến n = (5; -2; 7). (P) đi qua điểm B(−2; 3; 0) và có cặp vectơ chỉ phương là u = (2; 2; -1), v = (3; 1; 0). Thực hành 4 trang 38 Toán 12 Tập 2

Vận dụng 3 trang 38 Toán 12 Tập 2
Trong không gian Oxyz, cho hình lăng trụ OAB.O'A'B'. Biết O là gốc tọa độ, A(2; 0; 0), B(0; 3; 0), O'(0; 0; 5). Viết phương trình các mặt phẳng (O'AB) và (O'A'B'). Vận dụng 3 trang 38 Toán 12 Tập 2

Hoạt động khám phá 7 trang 38 Toán 12 Tập 2
Cho hai mặt phẳng (α), (β) có phương trình là (α): x – 2y + 3z + 1 = 0 và (β): 2x – 4y + 6z + 1 = 0. Nêu nhận xét về các vectơ pháp tuyến của hai mặt phẳng trên. Hoạt động khám phá 7 trang 38 Toán 12 Tập 2
Thực hành 5 trang 39 Toán 12 Tập 2
Mặt phẳng (E): 2x – y + 8z + 1 = 0 song song với mặt phẳng nào sau đây? Thực hành 5 trang 39 Toán 12 Tập 2

Vận dụng 4 trang 40 Toán 12 Tập 2
Trên bản thiết kế đồ họa 3D của một cách đồng điện mặt trời trong không gian Oxyz, một tấm pin nằm trên mặt phẳng (P): 6x + 5y + z + 2 = 0. Vận dụng 4 trang 40 Toán 12 Tập 2

Hoạt động khám phá 8 trang 40 Toán 12 Tập 2
Cho hai mặt phẳng (α) và (β) có phương trình là (α): 3x + 2y + z + 1 = 0 và (β): 5x – 10y + 5z + 9 = 0. Chỉ ra hai vectơ n1, n2 lần lượt là vectơ pháp tuyến của (α) và (β). Hoạt động khám phá 8 trang 40 Toán 12 Tập 2
Thực hành 6 trang 40 Toán 12 Tập 2
Tìm các cặp mặt phẳng vuông góc trong các mặt phẳng sau. (F): 3x + 2y + 5z + 3 = 0; (H): x – 4y + z + 23 = 0; (G): x – y + 3z + 24 = 0. Thực hành 6 trang 40 Toán 12 Tập 2

Vận dụng 5 trang 40 Toán 12 Tập 2
Hai học sinh đang chuyền bóng. Bạn nữ ném bóng cho bạn nam. Quả bóng bay trên không, lệch sang phải và rơi xuống tại vị trí cách bạn nam 3 m, cách bạn nữ 5 m (Hình 16). Vận dụng 5 trang 40 Toán 12 Tập 2

Hoạt động khám phá 9 trang 41 Toán 12 Tập 2
Trong không gian Oxyz, cho mặt phẳng (α) có phương trình Ax + By + Cz + D = 0 và điểm M0(x0; y0; z0). Gọi M1(x1; y1; z1) là hình chiếu vuông góc của M0 trên (α) (Hình 17). Hoạt động khám phá 9 trang 41 Toán 12 Tập 2
Thực hành 7 trang 42 Toán 12 Tập 2
Tính chiều cao của hình chóp O.MNP với tọa độ các đỉnh là O(0; 0; 0), M(2; 1; 2), N(3; 3; 3), P(4; 5; 6). Tính khoảng cách giữa hai mặt phẳng song song (R): 8x + 6y + 70 = 0 và (S): 16x + 12y – 2 = 0. Thực hành 7 trang 42 Toán 12 Tập 2

Vận dụng 6 trang 42 Toán 12 Tập 2
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a căn 2, chiều cao bằng 2a và O là tâm của đáy. Bằng cách thiết lập hệ trục tọa độ Oxyz như Hình 18, tính khoảng cách từ điểm C đến mặt phẳng (SAB). Vận dụng 6 trang 42 Toán 12 Tập 2
Giải bài tập Bài 2. Phương trình đường thẳng trong không gian

Bài 1 trang 59 Toán 12 Tập 2
Viết phương trình tham số của đường thẳng a trong mỗi trường hợp sau. Bài 1 trang 59 Toán 12 Tập 2

Bài 2 trang 59 Toán 12 Tập 2
Viết phương trình chính tắc của đường thẳng b trong mỗi trường hợp sau. Bài 2 trang 59 Toán 12 Tập 2

Bài 3 trang 59 Toán 12 Tập 2
Cho đường thẳng d có phương trình chính tắc, thực hiện các yêu cầu đề bài. Bài 3 trang 59 Toán 12 Tập 2
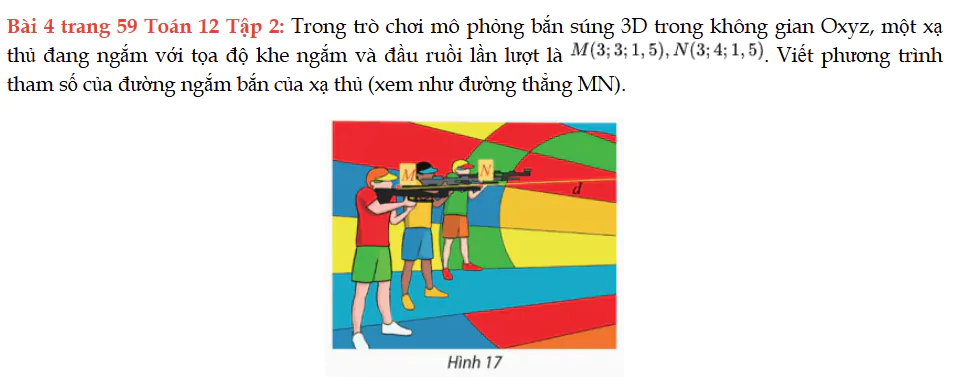
Bài 4 trang 59 Toán 12 Tập 2
Trong trò chơi mô phỏng bắn súng 3D trong không gian Oxyz, viết phương trình tham số của đường ngắm bắn của xạ thủ (xem như đường thẳng MN). Bài 4 trang 59 Toán 12 Tập 2
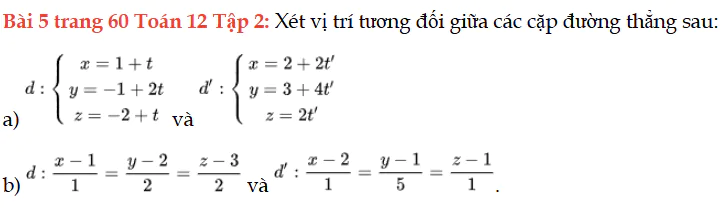
Bài 5 trang 60 Toán 12 Tập 2
Xét vị trí tương đối giữa các cặp đường thẳng sau. Bài 5 trang 60 Toán 12 Tập 2
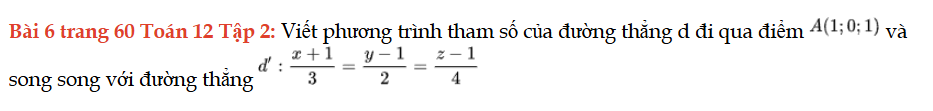
Bài 6 trang 60 Toán 12 Tập 2
Viết phương trình tham số của đường thẳng d đi qua điểm A và song song với đường thẳng d'. Bài 6 trang 60 Toán 12 Tập 2

Bài 7 trang 60 Toán 12 Tập 2
Trên phần mềm mô phỏng 3D một máy khoan trong không gian Oxyz, cho biết phương trình trục a của mũi khoan và một đường rãnh b trên vật cần khoan (Hình 18) lần lượt là. Bài 7 trang 60 Toán 12 Tập 2

Bài 8 trang 60 Toán 12 Tập 2
Tính góc giữa hai đường thẳng d và d'. Bài 8 trang 60 Toán 12 Tập 2

Bài 9 trang 60 Toán 12 Tập 2
Tính góc giữa đường thẳng d và mặt phẳng (P). Bài 9 trang 60 Toán 12 Tập 2

Bài 10 trang 60 Toán 12 Tập 2
Tính góc giữa hai mặt phẳng (P) và (P'). Bài 10 trang 60 Toán 12 Tập 2

Bài 11 trang 60 Toán 12 Tập 2
Trên một cánh đồng điện mặt trời, người ta đã thiết lập sẵn một hệ tọa độ Oxyz. Hai tấm pin năng lượng lần lượt nằm trong hai mặt phẳng (P). Bài 11 trang 60 Toán 12 Tập 2

Bài 12 trang 60 Toán 12 Tập 2
Trong không gian Oxyz, cho hình lăng trụ đứng OBC.O'B'C' có đáy là tam giác OBC vuông tại O. Cho biết B(3; 0; 0), C(0; 1; 0), O'(0; 0; 2). Tính góc giữa. Bài 12 trang 60 Toán 12 Tập 2

Hoạt động khởi động trang 43 Toán 12 Tập 2
Ta đã biết trong mặt phẳng Oxy, phương trình tham số của đường thẳng có dạng sau. Trong không gian Oxyz, phương trình tham số của đường thẳng có dạng như thế nào? Hoạt động khởi động trang 43 Toán 12 Tập 2

Hoạt động khám phá 1 trang 44 Toán 12 Tập 2
Trong không gian Oxyz, cho điểm M0 cố định và vectơ a khác 0. Có bao nhiêu đường thẳng d đi qua M0 và song song hoặc trùng với giá của a? Hoạt động khám phá 1 trang 44 Toán 12 Tập 2

Thực hành 1 trang 44 Toán 12 Tập 2
Trong không gian Oxyz, cho hình lăng trụ tam giác ABC.A'B'C' với A(1; 2; 1), B(7; 5; 3), C(4; 2; 0), A'(4; 9; 9). Tìm tọa độ một vectơ chỉ phương của mỗi đường thẳng AB, A'C' và BB'. Thực hành 1 trang 44 Toán 12 Tập 2

Hoạt động khám phá 2 trang 44 Toán 12 Tập 2
Trong không gian Oxyz, cho đường thẳng d đi qua điểm M0(x0; y0; z0) cố định và có vectơ chỉ phương là a =(a1, a2, a3) khác 0.Hoạt động khám phá 2 trang 44 Toán 12 Tập 2

Thực hành 2 trang 46 Toán 12 Tập 2
Cho đường thẳng d có phương trình tham số. Tìm hai vectơ chỉ phương của d. Tìm ba điểm trên d. Thực hành 2 trang 46 Toán 12 Tập 2
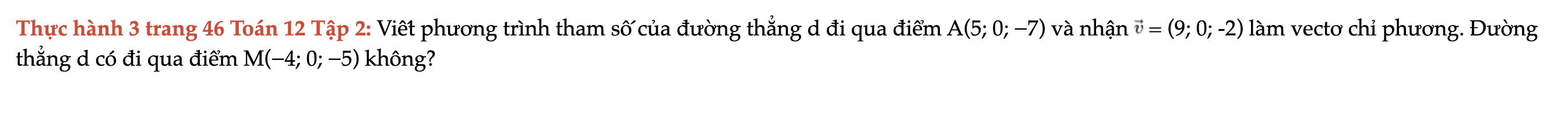
Thực hành 3 trang 46 Toán 12 Tập 2
Viết phương trình tham số của đường thẳng d đi qua điểm A(5; 0; −7) và nhận v = (9; 0; -2) làm vectơ chỉ phương. Đường thẳng d có đi qua điểm M(−4; 0; −5) không? Thực hành 3 trang 46 Toán 12 Tập 2

Hoạt động khám phá 3 trang 46 Toán 12 Tập 2
Cho đường thẳng d có phương trình tham số với a1, a2, a3 đều khác 0. Lấy điểm M(x; y; z) bất kì thuộc d. So sánh các biểu thức sau. Hoạt động khám phá 3 trang 46 Toán 12 Tập 2
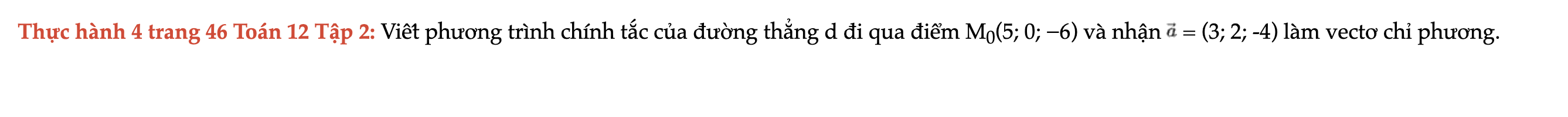
Thực hành 4 trang 46 Toán 12 Tập 2
Viết phương trình chính tắc của đường thẳng d đi qua điểm M0(5; 0; −6) và nhận vectơ a = (3; 2; -4) làm vectơ chỉ phương. Thực hành 4 trang 46 Toán 12 Tập 2

Hoạt động khám phá 4 trang 47 Toán 12 Tập 2
Cho đường thẳng d đi qua hai điểm A(2; 2; 1) và B(4; 5; 3). Tìm một vectơ chỉ phương của d. Viết phương trình tham số và phương trình chính tắc của d. Hoạt động khám phá 4 trang 47 Toán 12 Tập 2

Thực hành 5 trang 47 Toán 12 Tập 2
Viết phương trình tham số và phương trình chính tắc của đường thẳng MN, biết M(2; 0; −1) và N(4; 3; 1). Thực hành 5 trang 47 Toán 12 Tập 2

Vận dụng 1 trang 47 Toán 12 Tập 2
Một mô hình cầu treo được thiết kế trong không gian Oxyz như Hình 4. Viết phương trình tham số của đường thẳng d biểu diễn làn đường đi qua hai điểm M(4; 3; 20) và N(4; 1000; 20). Vận dụng 1 trang 47 Toán 12 Tập 2
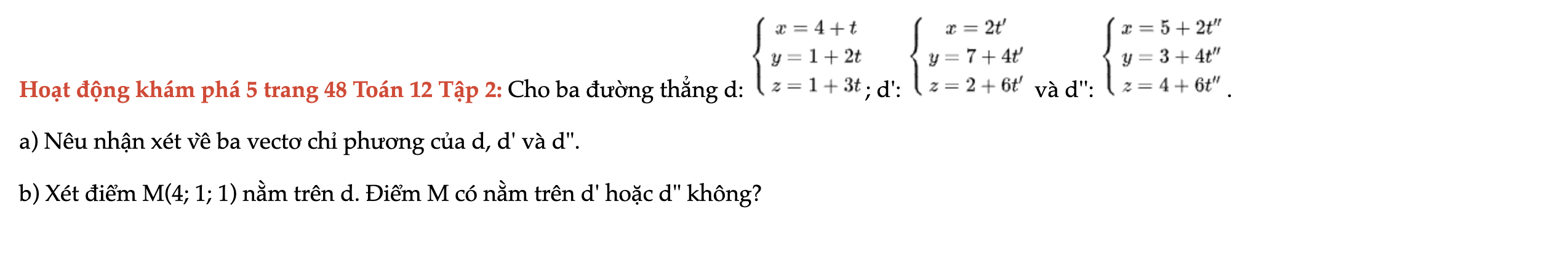
Hoạt động khám phá 5 trang 48 Toán 12 Tập 2
Cho ba đường thẳng d; d' và d'' theo dạng phương trình tham số. Nêu nhận xét về ba vectơ chỉ phương của d, d' và d". Xét điểm M(4; 1; 1) nằm trên d. Điểm M có nằm trên d' hoặc d" không? Hoạt động khám phá 5 trang 48 Toán 12 Tập 2

Thực hành 6 trang 49 Toán 12 Tập 2
Kiểm tra tính song song hoặc trùng nhau của các cặp đường thẳng sau. Thực hành 6 trang 49 Toán 12 Tập 2

Vận dụng 2 trang 49 Toán 12 Tập 2
Trên một máy khoan bàn đã thiết lập sẵn một hệ tọa độ. Nêu nhận xét về vị trí giữa trục d của mũi khoan và trục d' của giá đỡ có phương trình lần lượt là: d và d'. Vận dụng 2 trang 49 Toán 12 Tập 2

Hoạt động khám phá 6 trang 50 Toán 12 Tập 2
Cho ba đường thẳng d, d', d'' theo dạng phương trình tham số. Đường thẳng d' và đường thẳng d" có song song hay trùng với đường thẳng d không? Hoạt động khám phá 6 trang 50 Toán 12 Tập 2

Thực hành 7 trang 52 Toán 12 Tập 2
Xét vị trí tương đối giữa hai đường thẳng d và d' trong mỗi trường hợp sau. Thực hành 7 trang 52 Toán 12 Tập 2

Vận dụng 3 trang 52 Toán 12 Tập 2
Trên phần mềm thiết kế chiếc cầu treo, cho đường thẳng d trên trụ cầu và đường thẳng d' trên sàn cầu có phương trình lần lượt là: d và d'. Xét vị trí tương đối giữa d và d'. Vận dụng 3 trang 52 Toán 12 Tập 2
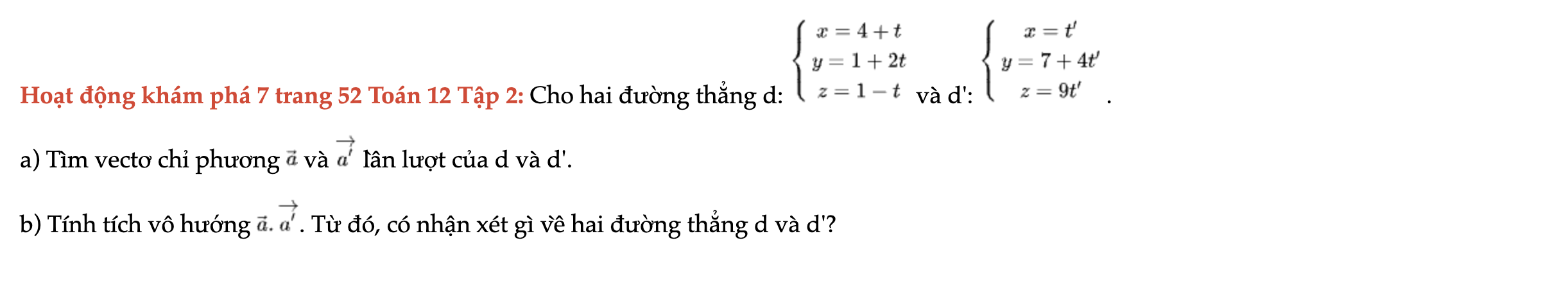
Hoạt động khám phá 7 trang 52 Toán 12 Tập 2
Cho hai đường thẳng d và d'. Tìm vectơ chỉ phương a và a' lần lượt của d và d'. Tính tích vô hướng a.a'. Từ đó, có nhận xét gì về hai đường thẳng d và d'? Hoạt động khám phá 7 trang 52 Toán 12 Tập 2

Thực hành 8 trang 53 Toán 12 Tập 2
Kiểm tra tính vuông góc của các cặp đường thẳng sau. Thực hành 8 trang 53 Toán 12 Tập 2

Vận dụng 4 trang 53 Toán 12 Tập 2
Một phần mềm mô phỏng vận động viên đang tập bắn súng trong không gian Oxyz. Cho biết trục d của nòng súng và cọc đỡ bia d' có phương trình lần lượt là d và d'. Vận dụng 4 trang 53 Toán 12 Tập 2

Hoạt động khám phá 8 trang 53 Toán 12 Tập 2
Cho hai đường thẳng d và d' có vectơ chỉ phương lần lượt là a = (2; 1; 3), a' = (3; 2; -8). Nhắc lại định nghĩa góc giữa hai đường thẳng d và d' trong không gian. Hoạt động khám phá 8 trang 53 Toán 12 Tập 2

Thực hành 9 trang 55 Toán 12 Tập 2
Tính góc giữa hai đường thẳng d và d' trong mỗi trường hợp sau. Thực hành 9 trang 55 Toán 12 Tập 2

Vận dụng 5 trang 55 Toán 12 Tập 2
Trên một phần mềm đã thiết kế sân khấu 3D trong không gian Oxyz. Tính góc giữa hai tia sáng có phương trình lần lượt là: d và d'. Vận dụng 5 trang 55 Toán 12 Tập 2

Hoạt động khám phá 9 trang 55 Toán 12 Tập 2
Cho đường thẳng d có vectơ chỉ phương a(a1, a2, a3) và mặt phẳng (P) có vectơ pháp tuyến n(n1, n2, n3). Biết d cắt (P) tại điểm N và hình chiếu vuông góc của d lên (P) là đường thẳng d'. Hoạt động khám phá 9 trang 55 Toán 12 Tập 2

Thực hành 10 trang 56 Toán 12 Tập 2
Tính góc giữa đường thẳng d và mặt phẳng (P) trong mỗi trường hợp sau. Thực hành 10 trang 56 Toán 12 Tập 2

Vận dụng 6 trang 56 Toán 12 Tập 2
Trên một sân khấu đã thiết lập sẵn một hệ tọa độ Oxyz. Tính góc giữa tia sáng có phương trình d và mặt sàn sân khấu có phương trình z = 0. Vận dụng 6 trang 56 Toán 12 Tập 2

Hoạt động khám phá 10 trang 57 Toán 12 Tập 2
Cho hai mặt phẳng (P) và (P') có vectơ pháp tuyến lần lượt là n và n' (Hình 14). Gọi d và d' là hai đường thẳng lần lượt vuông góc với (P) và (P'). Hoạt động khám phá 10 trang 57 Toán 12 Tập 2

Thực hành 11 trang 58 Toán 12 Tập 2
Tính góc giữa hai mặt phẳng (P) và (P') trong mỗi trường hợp sau. Thực hành 11 trang 58 Toán 12 Tập 2

Thực hành 12 trang 59 Toán 12 Tập 2
Trong không gian Oxyz, cho hình hộp chữ nhật ABCD.A'B'C'D'. Cho biết A(0; 0; 0), B(1; 0; 0), D(0; 5; 0), A'(0; 0; 3). Tính góc giữa hai đường thẳng AC và BA'; hai mặt phẳng (BB'D'D) và (AA'C'C). Thực hành 12 trang 59 Toán 12 Tập 2

Vận dụng 7 trang 59 Toán 12 Tập 2
Để làm thí nghiệm về chuyển động trong mặt phẳng nghiêng, người làm thí nghiệm đã thiết lập sẵn một hệ tọa độ Oxyz. Tính góc giữa mặt phẳng nghiêng (P): 4x + 11z + 5 = 0 và mặt sàn (Q): z – 1 = 0. Vận dụng 7 trang 59 Toán 12 Tập 2
Giải bài tập Bài 3. Phương trình mặt cầu

Bài 1 trang 65 Toán 12 Tập 2
Viết phương trình mặt cầu (S). Bài 1 trang 65 Toán 12 Tập 2

Bài 2 trang 65 Toán 12 Tập 2
Trong các phương trình sau, phương trình nào là phương trình mặt cầu? Xác định tâm và bán kính của mặt cầu đó. Bài 2 trang 65 Toán 12 Tập 2
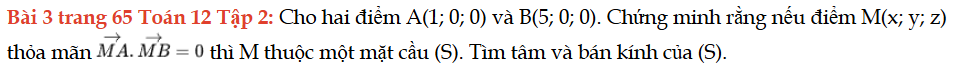
Bài 3 trang 65 Toán 12 Tập 2
Cho hai điểm A và B, chứng minh rằng nếu điểm M thỏa mãn yêu cầu đề bài. Tìm tâm và bán kính của (S). Bài 3 trang 65 Toán 12 Tập 2

Bài 4 trang 65 Toán 12 Tập 2
Phần mềm mô phỏng thiết bị thám hiểm đại dương có dạng hình cầu trong không gian Oxyz. Cho biết tọa độ tâm mặt cầu là I và bán kính r. Viết phương trình mặt cầu. Bài 4 trang 65 Toán 12 Tập 2

Bài 5 trang 65 Toán 12 Tập 2
gười ta muốn thiết kế một bồn chứa khí hóa lỏng hình cầu bằng phần mềm 3D. Cho biết phương trình bề mặt của bồn chứa là (S), phương trình mặt phẳng chứa nắp là (P). Bài 5 trang 65 Toán 12 Tập 2

Hoạt động khởi động trang 61 Toán 12 Tập 2
Trong không gian Oxyz, phương trình mặt cầu có dạng như thế nào? Hoạt động khởi động trang 61 Toán 12 Tập 2

Hoạt động khám phá 1 trang 61 Toán 12 Tập 2
Trong không gian Oxyz, cho mặt cầu S(I; R) có tâm I(a; b; c) và bán kính R. Xét một điểm M(x; y; z) thay đổi. Tính khoảng cách IM theo x, y, z và a, b, c. Hoạt động khám phá 1 trang 61 Toán 12 Tập 2

Thực hành 1 trang 62 Toán 12 Tập 2
Viết phương trình mặt cầu (S) có tâm I(3; −2; −4), bán kính R = 10; đường kính EF với E(3; −1; 8) và F(7; −3; 0); tâm M(−2; 1; 3) và đi qua điểm N(2; −3; −4). Thực hành 1 trang 62 Toán 12 Tập 2

Vận dụng 1 trang 62 Toán 12 Tập 2
Trong không gian Oxyz (đơn vị của các trục tọa độ là mét), các nhà nghiên cứu khí tượng dùng một phần mềm mô phỏng bề mặt của một quả bóng thám không có dạng hình cầu bằng phương trình như sau. Vận dụng 1 trang 62 Toán 12 Tập 2

Hoạt động khám phá 2 trang 63 Toán 12 Tập 2
Trong không gian Oxyz, cho điểm M(x; y; z) thay đổi có tọa độ luôn thỏa mãn phương trình sau. Hoạt động khám phá 2 trang 63 Toán 12 Tập 2

Thực hành 2 trang 63 Toán 12 Tập 2
Trong các phương trình sau, phương trình nào là phương trình mặt cầu? Xác định tâm và bán kính của mặt cầu đó. Thực hành 2 trang 63 Toán 12 Tập 2

Vận dụng 2 trang 64 Toán 12 Tập 2
Bề mặt của một bóng thám không dạng hình cầu có phương trình như sau. Tìm tọa độ tâm và bán kính mặt cầu. Vận dụng 2 trang 64 Toán 12 Tập 2

Vận dụng 3 trang 64 Toán 12 Tập 2
Đầu in phun của một máy in 3D đang in bề mặt của một mặt cầu có phương trình như sau. Tính khoảng cách từ đầu in phun đến tâm mặt cầu. Vận dụng 3 trang 64 Toán 12 Tập 2
Giải bài tập Bài tập cuối chương 5
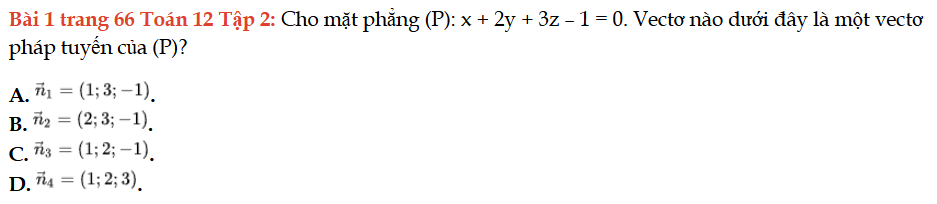
Bài 1 trang 66 Toán 12 Tập 2
Cho mặt phẳng (P), vectơ nào dưới đây là một vectơ pháp tuyến của (P)? Bài 1 trang 66 Toán 12 Tập 2

Bài 2 trang 66 Toán 12 Tập 2
Phương trình nào dưới đây là phương trình mặt phẳng (Oyz)? Bài 2 trang 66 Toán 12 Tập 2

Bài 3 trang 66 Toán 12 Tập 2
Phương trình nào dưới đây là phương trình mặt phẳng đi qua điểm M và có vectơ pháp tuyến. Bài 3 trang 66 Toán 12 Tập 2
Bài 4 trang 66 Toán 12 Tập 2
Cho mặt phẳng (P) và điểm A, khoảng cách từ A đến (P) bằng. Bài 4 trang 66 Toán 12 Tập 2

Bài 5 trang 66 Toán 12 Tập 2
Cho ba mặt phẳng, trong các mệnh đề sau, mệnh đề nào sai? Bài 5 trang 66 Toán 12 Tập 2
Bài 6 trang 66 Toán 12 Tập 2
Cho đường thẳng d, vectơ nào dưới đây là một vectơ chỉ phương của d? Bài 6 trang 66 Toán 12 Tập 2

Bài 7 trang 66 Toán 12 Tập 2
Phương trình nào dưới đây là phương trình chính tắc của đường thẳng d. Bài 7 trang 66 Toán 12 Tập 2

Bài 8 trang 66 Toán 12 Tập 2
Cho đường thẳng d, trong các đường thẳng sau, đường thẳng nào vuông góc với d? Bài 8 trang 66 Toán 12 Tập 2

Bài 9 trang 66 Toán 12 Tập 2
Cho hai mặt phẳng (P) và (Q), góc giữa hai mặt phẳng (P) và (Q) bằng. Bài 9 trang 66 Toán 12 Tập 2

Bài 10 trang 67 Toán 12 Tập 2
Cho mặt cầu (S), tọa độ tâm I và bán kính R của (S) là. Bài 10 trang 67 Toán 12 Tập 2

Bài 11 trang 67 Toán 12 Tập 2
Mặt cầu tâm I và đi qua điểm A có phương trình là. Bài 11 trang 67 Toán 12 Tập 2

Bài 12 trang 67 Toán 12 Tập 2
Cho bốn điểm A(1; 0; 0), B(0; 1; 0), C(0; 0; 1), D(−2; 1; −1). Bài 12 trang 67 Toán 12 Tập 2

Bài 13 trang 67 Toán 12 Tập 2
Cho bốn điểm A, B, C và D. Bài 13 trang 67 Toán 12 Tập 2
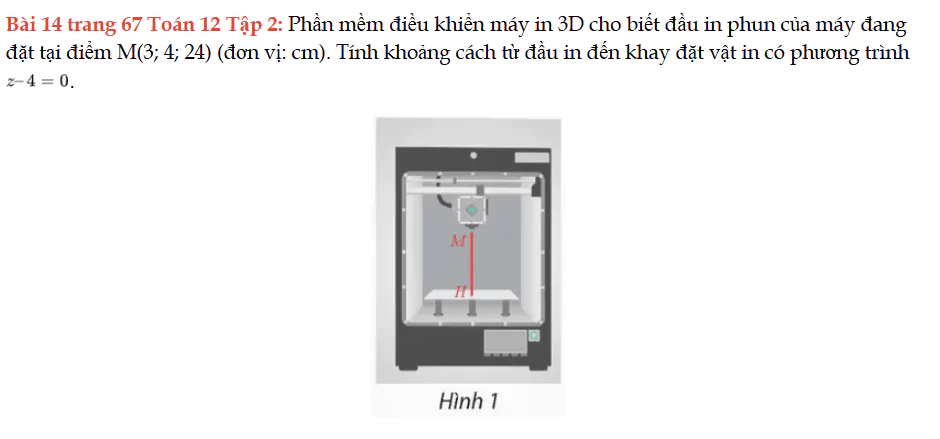
Bài 14 trang 67 Toán 12 Tập 2
Phần mềm điều khiển máy in 3D cho biết đầu in phun của máy đang đặt tại điểm M, tính khoảng cách từ đầu in đến khay đặt vật in có phương trình z – 4 = 0. Bài 14 trang 67 Toán 12 Tập 2

Bài 15 trang 67 Toán 12 Tập 2
Cho hai mặt phẳng (P) và (Q). Biết rằng điểm H là hình chiếu vuông góc của gốc tọa độ O xuống mặt phẳng (Q). Tính góc giữa mặt phẳng (P) và mặt phẳng (Q). Bài 15 trang 67 Toán 12 Tập 2
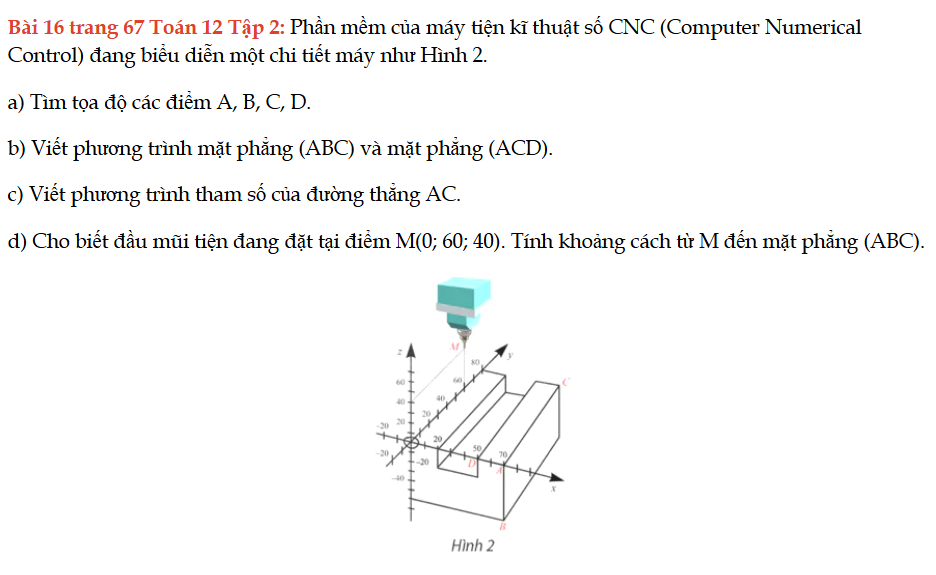
Bài 16 trang 67 Toán 12 Tập 2
Phần mềm của máy tiện kĩ thuật số CNC (Computer Numerical Control) đang biểu diễn một chi tiết máy như Hình 2. Bài 16 trang 67 Toán 12 Tập 2

Bài 17 trang 67 Toán 12 Tập 2
Cho hình hộp chữ nhật OABC.O'A'B'C', với O là gốc tọa độ, A(2; 0; 0), C(0; 6; 0), O'(0; 0; 4), viết phương trình. Bài 17 trang 67 Toán 12 Tập 2
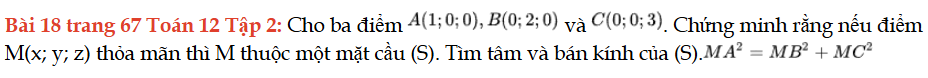
Bài 18 trang 67 Toán 12 Tập 2
Cho ba điểm A(1; 0; 0), B(0; 2; 0) và C(0; 0; 3). Chứng minh rằng nếu điểm M(x; y; z) thỏa mãn thì M thuộc một mặt cầu (S). Tìm tâm và bán kính của (S). Bài 18 trang 67 Toán 12 Tập 2