Giải bài tập Hoạt động khám phá 8 trang 40 Toán 12 Tập 2 | SGK Toán 12 - Chân trời sáng tạo
Hướng dẫn giải chi tiết từng bước bài tập Hoạt động khám phá 8 trang 40 Toán 12 Tập 2. Bài 1. Phương trình mặt phẳng. SGK Toán 12 - Chân trời sáng tạo
Đề bài:
Cho hai mặt phẳng (α) và (β) có phương trình là (α): 3x + 2y + z + 1 = 0 và (β): 5x – 10y + 5z + 9 = 0.
a) Chỉ ra hai vectơ 
lần lượt là vectơ pháp tuyến của (α) và (β).
b) Tính tích vô hướng và nêu nhận xét về hai mặt phẳng (α) và (β).
Đáp án và cách giải chi tiết:
a) Có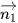 
= (3; 2; 1), 
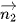= (5; -10; 5).
b)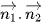 
= 3.5 + 2.(-10) +1.5 = 0.
Do đó (α) ⊥ (β).
Nguồn: loigiaitoan.com
Tổng số đánh giá:
Xếp hạng: / 5 sao
Bài tập liên quan:
Bài 1 trang 42 Toán 12 Tập 2
Bài 1 trang 42 Toán 12 Tập 2: Viết phương trình của mặt phẳng:
a) Đi qua điểm 
và nhận 
làm vectơ pháp tuyến;
b) Đi qua điểm 
và song song với giá của mỗi vectơ 
và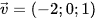 
;
c) Đi qua ba điểm 
và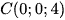 
.
Bài 2 trang 42 Toán 12 Tập 2
Bài 2 trang 42 Toán 12 Tập 2:
a) Lập phương trình của các mặt phẳng tọa độ (Oxy), (Oyz), (Oxz).
b) Lập phương trình của các mặt phẳng đi qua điểm A(−1; 9; 8) và lần lượt song song với các mặt phẳng tọa độ trên.
Bài 3 trang 42 Toán 12 Tập 2
Bài 3 trang 42 Toán 12 Tập 2: Cho tứ diện ABCD có các đỉnh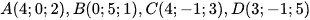 
.
a) Hãy viết phương trình của các mặt phẳng (ABC) và (ABD).
b) Hãy viết phương trình mặt phẳng (P) đi qua cạnh BC và song song với cạnh AD.
Bài 4 trang 42 Toán 12 Tập 2
Bài 4 trang 42 Toán 12 Tập 2: Viết phương trình mặt phẳng (Q) đi qua 
và song song với mặt phẳng 
Bài 5 trang 42 Toán 12 Tập 2
Bài 5 trang 42 Toán 12 Tập 2: Viết phương trình mặt phẳng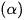 
đi qua hai điểm 
và vuông góc với mặt phẳng 
.
Bài 6 trang 42 Toán 12 Tập 2
Bài 6 trang 42 Toán 12 Tập 2: Viết phương trình mặt phẳng (R) đi qua điểm 
và vuông góc với hai mặt phẳng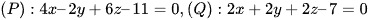 
.
Bài 7 trang 43 Toán 12 Tập 2
Bài 7 trang 43 Toán 12 Tập 2: Tính khoảng cách từ gốc tọa độ và từ điểm 
đến mặt phẳng 
.
Bài 8 trang 43 Toán 12 Tập 2
Bài 8 trang 43 Toán 12 Tập 2: Tính khoảng cách giữa hai mặt phẳng song song 
và 
.
Bài 9 trang 43 Toán 12 Tập 2
Bài 9 trang 43 Toán 12 Tập 2: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với 
và 
. Bằng cách thiết lập hệ trục tọa độ Oxyz như Hình 19, tính khoảng cách từ điểm A đến mặt phẳng (SBC).
Bài 10 trang 43 Toán 12 Tập 2
Bài 10 trang 43 Toán 12 Tập 2: Một công trường xây dựng nhà cao tầng đã thiết lập hệ tọa độ Oxyz. Hãy kiểm tra tính song song hoặc vuông góc giữa các mặt kính (P), (Q), (R) (Hình 20) của một tòa nhà, biết: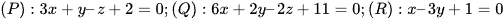 
.
Hoạt động khởi động trang 32 Toán 12 Tập 2
Trong không gian Oxyz, làm thế nào để xác định một mặt phẳng bằng phương pháp tọa độ?
Hoạt động khám phá 1 trang 32 Toán 12 Tập 2
a) Cho vectơ 
khác 
. Qua một điểm M0 cố định trong không gian, có bao nhiêu mặt phẳng (α) vuông góc với giá của vectơ ?
b) Cho hai vectơ 
không cùng phương. Qua một điểm M0 cố định trong không gian, có bao nhiêu mặt phẳng (α) song song hoặc chứa giá của hai vectơ ?
Thực hành 1 trang 33 Toán 12 Tập 2
Trong không gian Oxyz, cho ba điểm A(3; 0; 0), B(0; 4; 0), C(0; 0; 5).
a) Tìm tọa độ của một cặp vectơ chỉ phương của mặt phẳng (ABC).
b) Tìm tọa độ của một vectơ pháp tuyến của mặt phẳng (OAB).
Vận dụng 1 trang 33 Toán 12 Tập 2
Một lăng kính có dạng hình lăng trụ đứng có đáy là tam giác đều ở Hình 3a được vẽ lại như Hình 3b. Tìm một cặp vectơ chỉ phương và một vectơ pháp tuyến của mặt phẳng (A'B'C').
Hoạt động khám phá 2 trang 33 Toán 12 Tập 2
Trong không gian Oxyz, cho mặt phẳng (α) có cặp vectơ chỉ phương 
. Xét vectơ 
.
a) Vectơ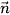 
có khác 
hay không?
b) Tính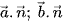 
c) Vectơ 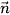có phải là vectơ pháp tuyến của mặt phẳng (α) không?
Thực hành 2 trang 34 Toán 12 Tập 2
Cho mặt phẳng (Q) đi qua ba điểm A(1; 1; 1), B(−1; 1; 5), C(10; 7; −1). Tìm cặp vectơ chỉ phương và một vectơ pháp tuyến của (Q).
Vận dụng 2 trang 34 Toán 12 Tập 2
Cho biết hai vectơ 
= (2; 1; 1), 
= (1; -2; 0) có giá lần lượt song song với ngón trỏ và ngón giữa của bàn tay trong Hình 5. Tìm vectơ 
có giá song song với ngón cái. (Xem như ba ngón tay nói trên tạo thành ba đường thẳng đôi một vuông góc).
Hoạt động khám phá 3 trang 35 Toán 12 Tập 2
Trong không gian Oxyz, cho mặt phẳng (α) đi qua điểm M0(1; 2; 3) và nhận 
= (7; 5; 2) làm vectơ pháp tuyến. Gọi M(x; y; z) là một điểm tùy ý trong không gian. Tính tích vô hướng 
theo x, y, z.
Thực hành 3 trang 36 Toán 12 Tập 2
Cho hai mặt phẳng (α), (β) có phương trình tổng quát là (α): 2x + 2y – 3z – 4 = 0 và (β): x + 4z – 12 = 0.
a) Tìm một vectơ pháp tuyến của mỗi mặt phẳng (α), (β).
b) Tìm điểm thuộc mặt phẳng (α) trong số các điểm: M(1; 0; 1), N(1; 1; 0).
Hoạt động khám phá 4 trang 36 Toán 12 Tập 2
Trong không gian Oxyz, cho mặt phẳng (α) đi qua điểm 
và nhận 
= (A; B; C) làm vectơ pháp tuyến. Gọi M(x; y; z) là một điểm tùy ý trong không gian.
a) Tìm tọa độ của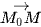 
.
b) Tính tích vô hướng của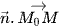 
.
c) Lập phương trình tổng quát của mặt phẳng (α).
