Giải bài tập Toán 12 Chương 4. Nguyên hàm. Tích phân. | Chân trời sáng tạo
Hướng dẫn giải Chương IV. Nguyên hàm. Tích phân. Khái niệm và tính chất cơ bản của Nguyên hàm, tích phân. Xác định nguyên hàm hàm số cơ bản, tính được tích phân cơ bản. Ứng dụng tích phân để tính diện tích hình phẳng, thể tích và bài toán thực tế.
Giải bài tập Bài 1. Nguyên hàm.
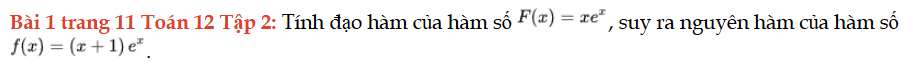
Bài 1 trang 11 Toán 12 Tập 2
Tính đạo hàm của hàm số y = F(x), suy ra nguyên hàm của hàm số y = f(x). Bài 1 trang 11 Toán 12 Tập 2
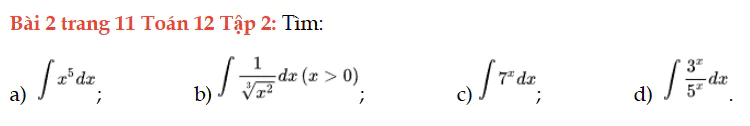
Bài 2 trang 11 Toán 12 Tập 2
Tìm nguyên hàm của các hàm số sau. Bài 2 trang 11 Toán 12 Tập 2
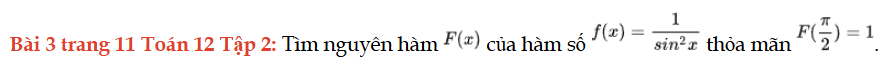
Bài 3 trang 11 Toán 12 Tập 2
Tìm nguyên hàm F(x) cảu hàm số y = f(x) thỏa mãn yêu cầu đề bài. Bài 3 trang 11 Toán 12 Tập 2

Bài 4 trang 11 Toán 12 Tập 2
Tìm nguyên hàm của các hàm số sau. Bài 4 trang 11 Toán 12 Tập 2

Bài 5 trang 12 Toán 12 Tập 2
Tìm nguyên hàm của các hàm số sau. Bài 5 trang 12 Toán 12 Tập 2

Bài 6 trang 12 Toán 12 Tập 2
Kí hiệu h(x) là chiều cao của một cây (tính theo mét) sau khi trồng x năm. Biết rằng sau năm đầu tiên cây cao 2 m. Trong 10 năm tiếp theo, cây phát triển với tốc độ, hãy thực hiệ các yêu cầu đề bài. Bài 6 trang 12 Toán 12 Tập 2

Bài 7 trang 12 Toán 12 Tập 2
Một chiếc xe đang chuyển động với vận tốc v thì tăng tốc với gia tốc không đổi a. Tính quãng đường xe đó đi được trong 3 giây kể từ khi bắt đầu tăng tốc. Bài 7 trang 12 Toán 12 Tập 2

Hoạt động khởi động trang 6 Toán 12 Tập 2
Khi được thả từ độ cao 20 m, một vật rơi với gia tốc không đổi a = 10 m/s2. Sau khi rơi được t giây thì vật có tốc độ bao nhiêu và đi được quãng đường bao nhiêu? Hoạt động khởi động trang 6 Toán 12 Tập 2
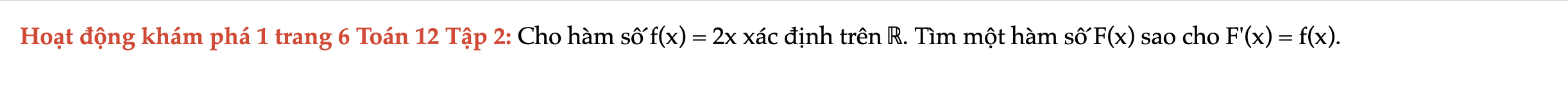
Hoạt động khám phá 1 trang 6 Toán 12 Tập 2
Cho hàm số f(x) = 2x xác định trên ℝ. Tìm một hàm số F(x) sao cho F'(x) = f(x). Hoạt động khám phá 1 trang 6 Toán 12 Tập 2

Hoạt động khám phá 2 trang 6 Toán 12 Tập 2
Cho hàm số f(x) = 3x^2 xác định trên ℝ. Chứng minh rằng F(x) = x^3 là một nguyên hàm của f(x) trên ℝ. Với C là hằng số tùy ý, hàm số H(x) = F(x) + C có là nguyên hàm của f(x) trên ℝ không? Hoạt động khám phá 2 trang 6 Toán 12 Tập 2
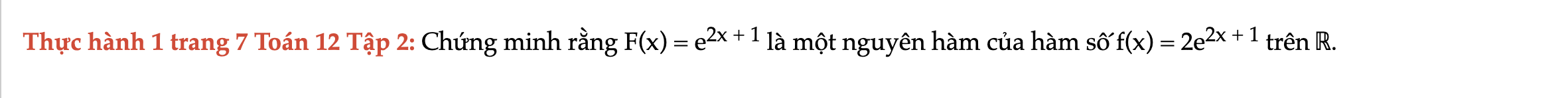
Thực hành 1 trang 7 Toán 12 Tập 2
Chứng minh rằng F(x) là một nguyên hàm của hàm số f(x) trên ℝ. Thực hành 1 trang 7 Toán 12 Tập 2
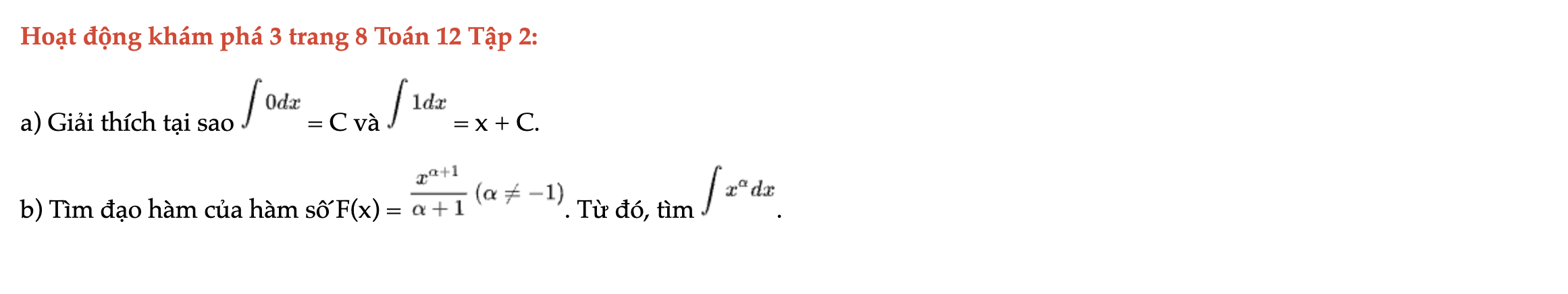
Hoạt động khám phá 3 trang 8 Toán 12 Tập 2
Tìm đạo hàm của hàm số F(x). Hoạt động khám phá 3 trang 8 Toán 12 Tập 2

Thực hành 2 trang 8 Toán 12 Tập 2
Tìm các nguyên hàm sau. Thực hành 2 trang 8 Toán 12 Tập 2
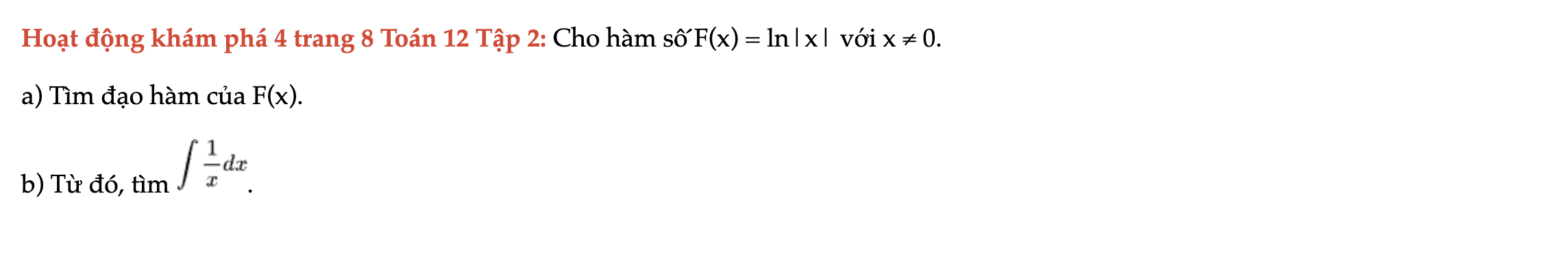
Hoạt động khám phá 4 trang 8 Toán 12 Tập 2
Cho hàm số F(x) = ln|x| với x ≠ 0. Tìm đạo hàm của F(x). Hoạt động khám phá 4 trang 8 Toán 12 Tập 2
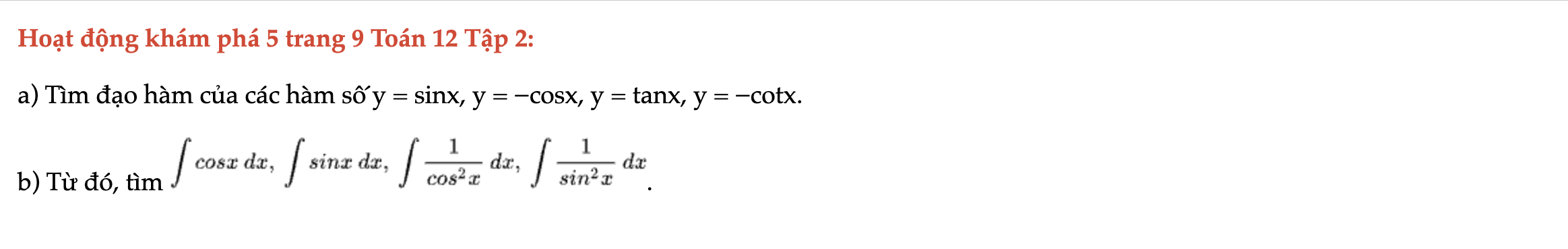
Hoạt động khám phá 5 trang 9 Toán 12 Tập 2
Tìm đạo hàm của các hàm số y = sinx, y = −cosx, y = tanx, y = −cotx. Hoạt động khám phá 5 trang 9 Toán 12 Tập 2
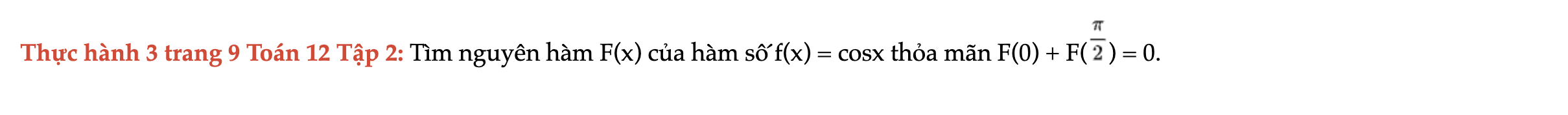
Thực hành 3 trang 9 Toán 12 Tập 2
Tìm nguyên hàm F(x) của hàm số f(x) = cosx thỏa mãn F(0) + F(π/2) = 0. Thực hành 3 trang 9 Toán 12 Tập 2

Hoạt động khám phá 6 trang 9 Toán 12 Tập 2
Tìm đạo hàm của các hàm số sau với a > 0, a ≠ 1. Hoạt động khám phá 6 trang 9 Toán 12 Tập 2

Thực hành 4 trang 9 Toán 12 Tập 2
Tìm các nguyên hàm sau. Thực hành 4 trang 9 Toán 12 Tập 2
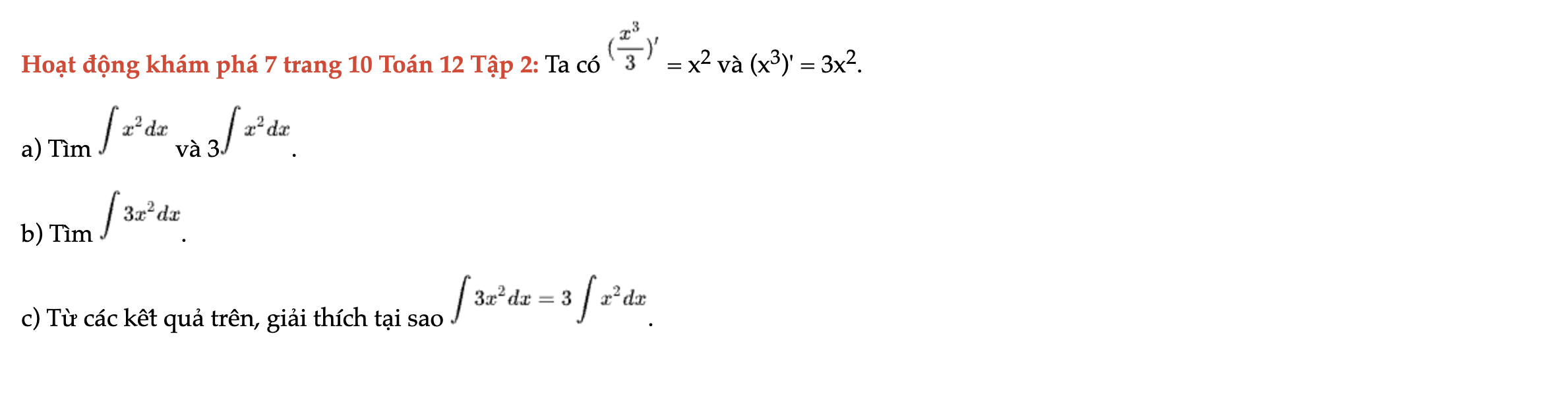
Hoạt động khám phá 7 trang 10 Toán 12 Tập 2
Hoạt động khám phá 7 trang 10 Toán 12 Tập 2

Thực hành 5 trang 10 Toán 12 Tập 2
Tìm các nguyên hàm sau. Thực hành 5 trang 10 Toán 12 Tập 2
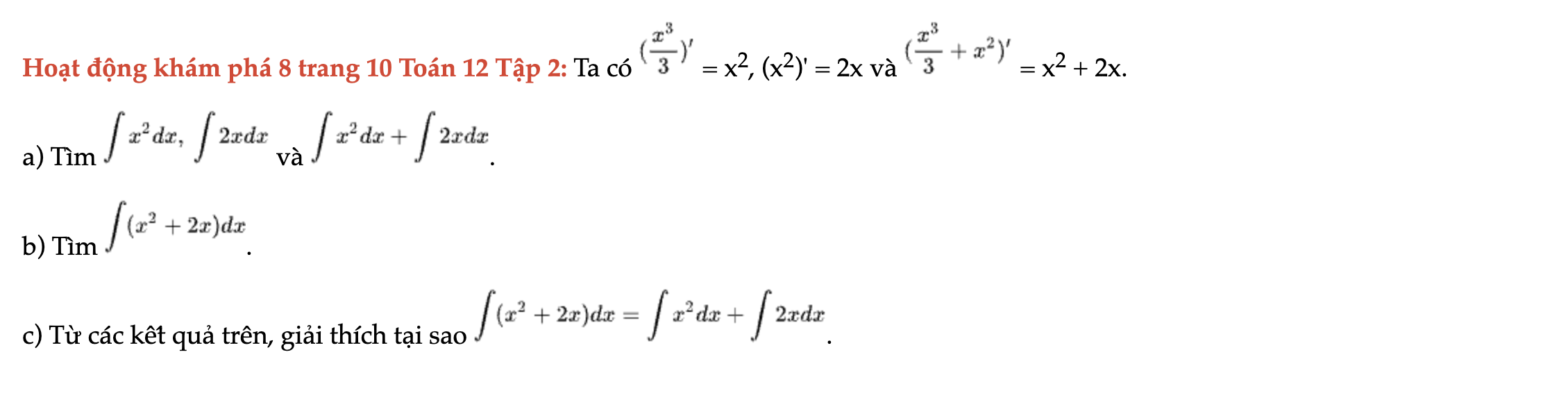
Hoạt động khám phá 8 trang 10 Toán 12 Tập 2
Hoạt động khám phá 8 trang 10 Toán 12 Tập 2

Thực hành 6 trang 11 Toán 12 Tập 2
Tìm các nguyên hàm sau. Thực hành 6 trang 11 Toán 12 Tập 2

Thực hành 7 trang 11 Toán 12 Tập 2
Một ô tô đang chạy với tốc độ 19 m/s thì hãm phanh và chuyển động chậm dần với tốc độ v(t) = 19 – 2t (m/s). Kể từ khi hãm phanh, quãng đường ô tô đi được sau 1 giây, 2 giây, 3 giây là bao nhiêu? Thực hành 7 trang 11 Toán 12 Tập 2
Giải bài tập Bài 2. Tích phân.
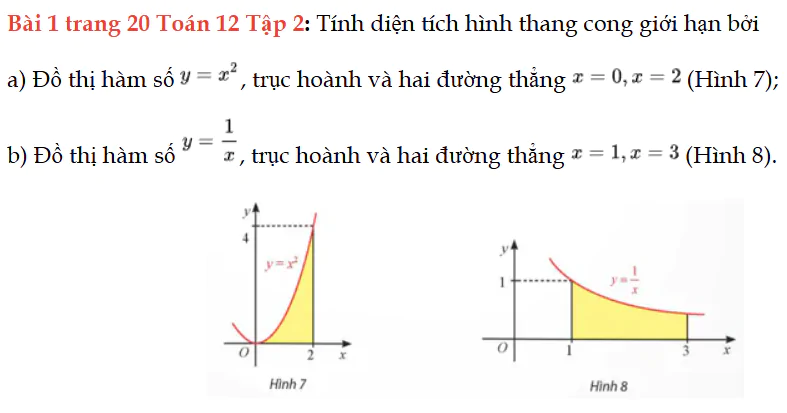
Bài 1 trang 20 Toán 12 Tập 2
Tính các tích phân sau. Bài 1 trang 20 Toán 12 Tập 2

Bài 2 trang 20 Toán 12 Tập 2
Tính các tích phân sau. Bài 2 trang 20 Toán 12 Tập 2

Bài 3 trang 20 Toán 12 Tập 2
Tính các tích phân sau. Bài 3 trang 20 Toán 12 Tập 2

Bài 4 trang 20 Toán 12 Tập 2
Tính các tích phân sau. Bài 4 trang 20 Toán 12 Tập 2

Bài 5 trang 20 Toán 12 Tập 2
Mặt cắt ngang của một ống dẫn khí nóng là hình vành khuyên như Hình 9. Khí bên trong ống được duy trì ở 150°C. Tìm nhiệt độ mặt ngoài của ống. Bài 5 trang 20 Toán 12 Tập 2

Bài 6 trang 20 Toán 12 Tập 2
Giả sử tốc độ v (m/s) của một thang máy di chuyển từ tầng 1 lên tầng cao nhất theo thời gian t (giây) được cho bởi công thức sau, tính quãng đường chuyển động và tốc độ trung bình của thang máy. Bài 6 trang 20 Toán 12 Tập 2

Hoạt động khởi động trang 12 Toán 12 Tập 2
Một ô tô đang di chuyển với vận tốc 20 m/s thì hãm phanh nên tốc độ (m/s) của xe thay đổi theo thời gian t (giây) được tính theo công thức v(t) = 20 – 5t (0 ≤ t ≤ 4). Hoạt động khởi động trang 12 Toán 12 Tập 2

Hoạt động khám phá 1 trang 12 Toán 12 Tập 2
Cho hàm số y = f(x) = x + 1. Với mỗi x ≥ 1, kí hiệu S(x) là diện tích của hình thang giới hạn bởi đồ thị hàm số y = f(x), trục hoành và hai đường thẳng vuông góc với Ox tại các điểm có hoành độ 1 và x. Tính S(3).Hoạt động khám phá 1 trang 12 Toán 12 Tập 2

Thực hành 1 trang 13 Toán 12 Tập 2
Tính diện tích hình thang cong giới hạn bởi đồ thị hàm số y = f(x) = e^x, trục hoành, trục tung và đường thẳng x = 1 (Hình 4). Thực hành 1 trang 13 Toán 12 Tập 2

Hoạt động khám phá 2 trang 14 Toán 12 Tập 2
Cho hàm số f(x) = 2x – 1. Lấy hai nguyên hàm tùy ý F(x) và G(x) của f(x), rồi tính F(3) – F(0) và G(3) – G(0). Nhận xét về kết quả nhận được. Hoạt động khám phá 2 trang 14 Toán 12 Tập 2

Thực hành 2 trang 16 Toán 12 Tập 2
Tính các tích phân sau. Thực hành 2 trang 16 Toán 12 Tập 2

Vận dụng 1 trang 16 Toán 12 Tập 2
Sau khi xuất phát, ô tô di chuyển với tốc độ v(t) = 2t - 0,03t^2 (0 ≤ t ≤ 10), trong đó v(t) tính theo m/s, thời gian t tính theo giây với t = 0 là thời điểm xe xuất phát. Vận dụng 1 trang 16 Toán 12 Tập 2
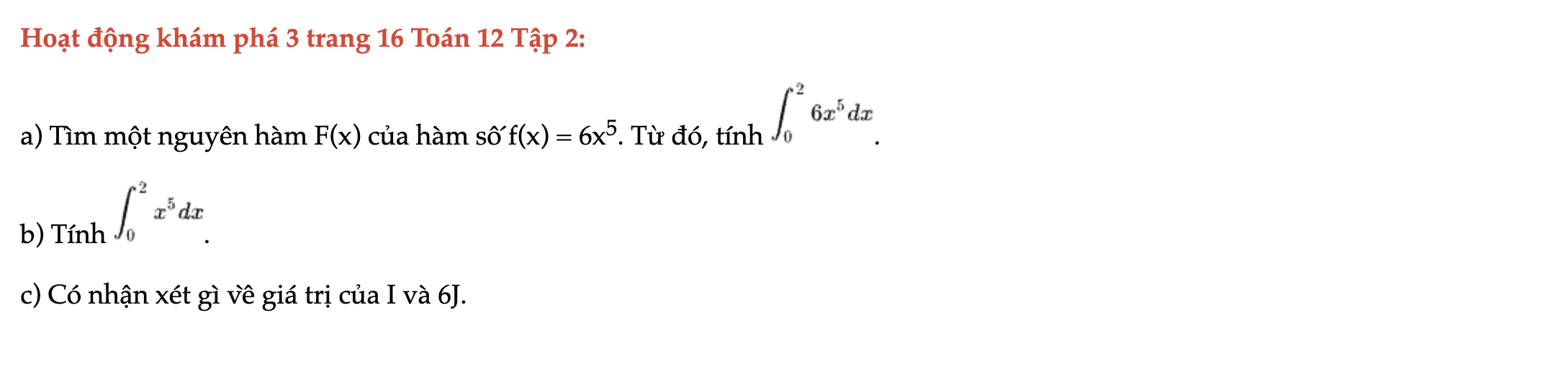
Hoạt động khám phá 3 trang 16 Toán 12 Tập 2
Tìm một nguyên hàm F(x) của hàm số f(x) = 6x^5. Và tính các tích phân đã cho. Hoạt động khám phá 3 trang 16 Toán 12 Tập 2

Thực hành 3 trang 17 Toán 12 Tập 2
Tính các tích phân sau. Thực hành 3 trang 17 Toán 12 Tập 2
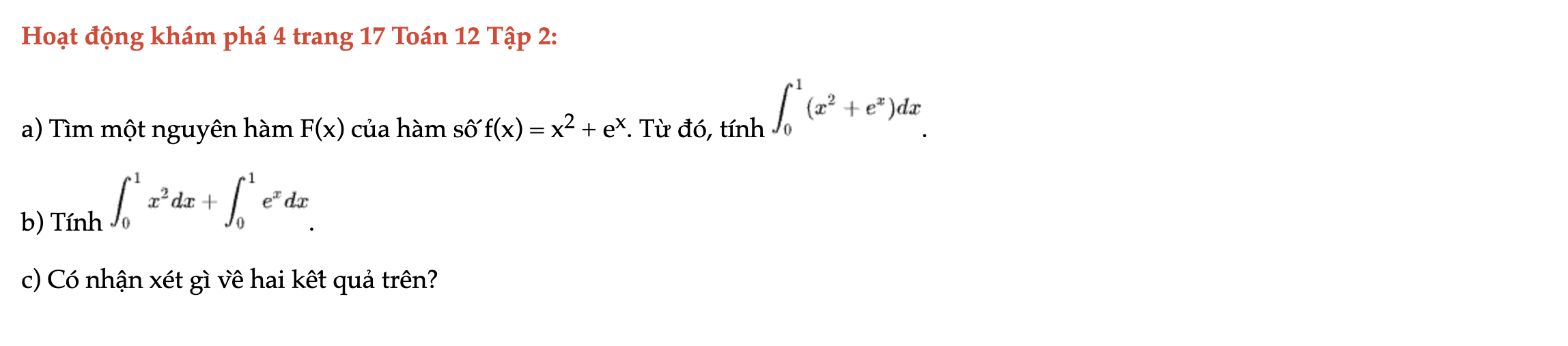
Hoạt động khám phá 4 trang 17 Toán 12 Tập 2
Tìm một nguyên hàm F(x) của hàm số f(x) = x2 + e^x. Từ đó, tính các tích phân sau. Hoạt động khám phá 4 trang 17 Toán 12 Tập 2

Thực hành 4 trang 18 Toán 12 Tập 2
Tính các tích phân sau. Thực hành 4 trang 18 Toán 12 Tập 2

Vận dụng 2 trang 18 Toán 12 Tập 2
Tại một nhà máy sản xuất một loại phân bón, gọi P(x) là lợi nhuận (tính theo triệu đồng) thu được từ việc bán x tấn sản phẩm trong một tuần. Vận dụng 2 trang 18 Toán 12 Tập 2

Hoạt động khám phá 5 trang 18 Toán 12 Tập 2
Cho hàm số f(x) = 2x. Tính và so sánh các kết quả sau. Hoạt động khám phá 5 trang 18 Toán 12 Tập 2

Thực hành 5 trang 19 Toán 12 Tập 2
Tính các tích phân sau. Thực hành 5 trang 19 Toán 12 Tập 2

Vận dụng 3 trang 19 Toán 12 Tập 2
Biết rằng tốc độ v (km/phút) của một ca nô cao tốc thay đổi theo thời gian t (phút) như sau: v(t). Tính quãng đường ca nô di chuyển được trong khoảng thời gian từ 0 đến 20 phút. Vận dụng 3 trang 19 Toán 12 Tập 2
Giải bài tập Bài 3. Ứng dụng hình học của tích phân.

Bài 1 trang 27 Toán 12 Tập 2
Tính diên tích hình phẳng giưới hạn bởi đồ thị của hàm số, trục hoành và hai đường thẳng. Bài 1 trang 27 Toán 12 Tập 2
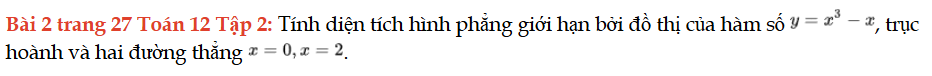
Bài 2 trang 27 Toán 12 Tập 2
Tính diện tích hình phẳng giới hạn bởi đồ thị của hàm số, trục hoành và hai đường thẳng. Bài 2 trang 27 Toán 12 Tập 2
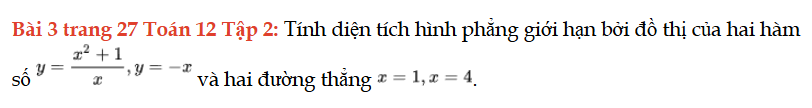
Bài 3 trang 27 Toán 12 Tập 2
Tính diện tích hình phẳng giới hạn bởi đồ thị của hai hàm số và hai đường thẳng. Bài 3 trang 27 Toán 12 Tập 2
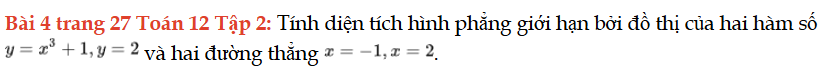
Bài 4 trang 27 Toán 12 Tập 2
Tính diện tích hình phẳng giới hạn bởi đồ thị của hai hàm số và hai đường thẳng. Bài 4 trang 27 Toán 12 Tập 2
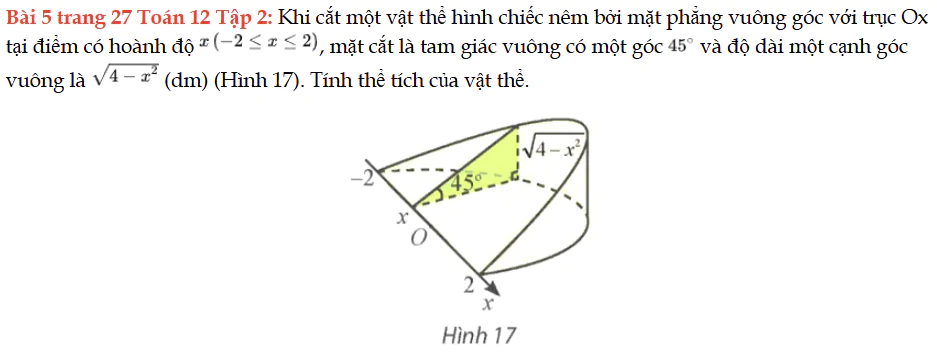
Bài 5 trang 27 Toán 12 Tập 2
Khi cắt một vật thể hình chiếc nêm bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x, tính thể tích của vật thể. Bài 5 trang 27 Toán 12 Tập 2
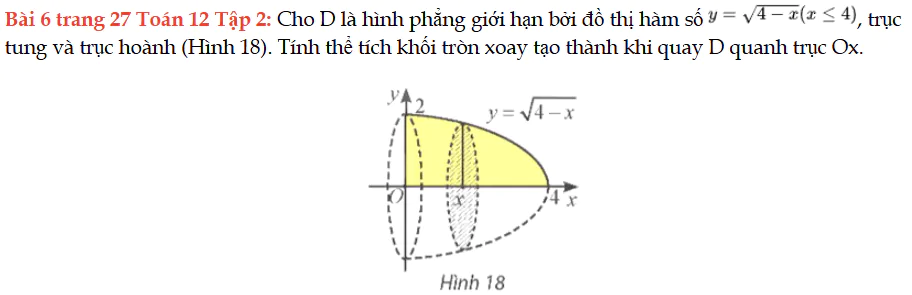
Bài 6 trang 27 Toán 12 Tập 2
Cho D là hình phẳng giới hạn bởi đồ thị hàm số, trục tung và trục hoành (Hình 18). Tính thể tích khối tròn xoay tạo thành khi quay D quanh trục Ox. Bài 6 trang 27 Toán 12 Tập 2
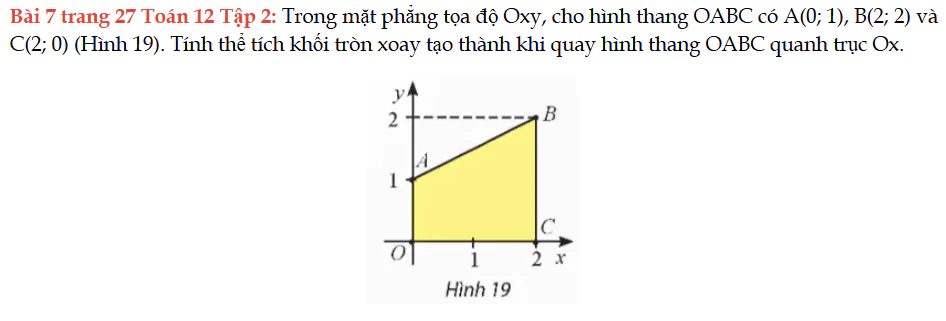
Bài 7 trang 27 Toán 12 Tập 2
Trong mặt phẳng tọa độ Oxy, cho hình thang OABC có A(0; 1), B(2; 2) và C(2; 0) (Hình 19). Tính thể tích khối tròn xoay tạo thành khi quay hình thang OABC quanh trục Ox. Bài 7 trang 27 Toán 12 Tập 2
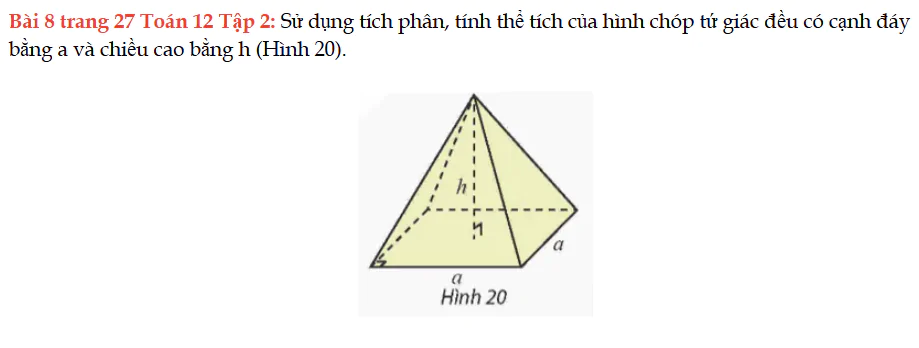
Bài 8 trang 27 Toán 12 Tập 2
Sử dụng tích phân, tính thể tích của hình chóp tứ giác đều có cạnh đáy bằng a và chiều cao bằng h (Hình 20). Bài 8 trang 27 Toán 12 Tập 2

Hoạt động khởi động trang 21 Toán 12 Tập 2
Ta đã biết công thức tính thể tích của khối cầu bán kính R là V. Làm thế nào để tìm ra công thức đó? Hoạt động khởi động trang 21 Toán 12 Tập 2

Hoạt động khám phá 1 trang 21 Toán 12 Tập 2
Gọi d là đồ thị của hàm số y = f(x) = 6 – 2x. Kí hiệu S1 là diện tích hình phẳng giới hạn bởi d, trục hoành và trục tung, S2 là diện tích hình phẳng giới hạn bởi d, trục hoành và đường thẳng x = 5 (Hình 1). Hoạt động khám phá 1 trang 21 Toán 12 Tập 2
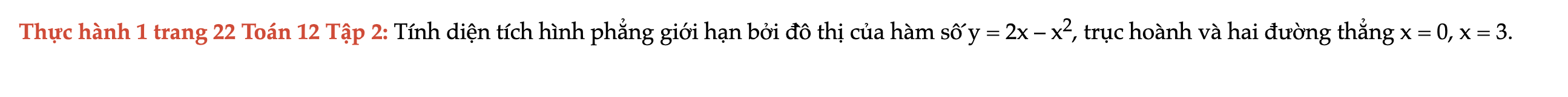
Thực hành 1 trang 22 Toán 12 Tập 2
Tính diện tích hình phẳng giới hạn bởi đồ thị của hàm số y = 2x – x2, trục hoành và hai đường thẳng x = 0, x = 3. Thực hành 1 trang 22 Toán 12 Tập 2

Thực hành 2 trang 22 Toán 12 Tập 2
Tính diện tích hình phẳng giới hạn bởi đồ thị của hàm số y = cosx – 2, trục hoành và hai đường thẳng x = 0, x = π. Thực hành 2 trang 22 Toán 12 Tập 2

Hoạt động khám phá 2 trang 23 Toán 12 Tập 2
Cho hai hàm số y = 4x – x^2 và y = x lần lượt có đồ thị (P) và d như Hình 4. Tính diện tích S1 của hình phẳng giới hạn bởi (P), trục hoành và hai đường thẳng x = 0, x = 2. Hoạt động khám phá 2 trang 23 Toán 12 Tập 2

Thực hành 3 trang 24 Toán 12 Tập 2
Tính diện tích hình phẳng giới hạn bởi đồ thị của hai hàm số y = x2 – 2x – 1, y = x – 1 và hai đường thẳng x = 1, x = 4. Thực hành 3 trang 24 Toán 12 Tập 2
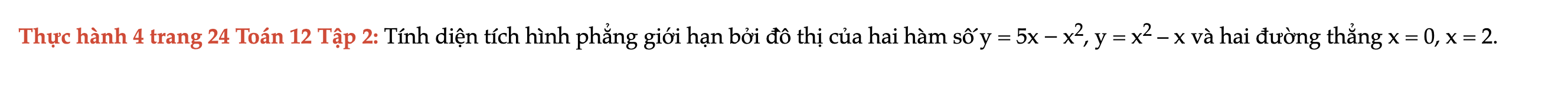
Thực hành 4 trang 24 Toán 12 Tập 2
Tính diện tích hình phẳng giới hạn bởi đồ thị của hai hàm số y = 5x − x2, y = x2 – x và hai đường thẳng x = 0, x = 2. Thực hành 4 trang 24 Toán 12 Tập 2

Vận dụng 1 trang 24 Toán 12 Tập 2
Mặt cắt của một cửa hầm có dạng là hình phẳng giới hạn bởi một parabol và đường thẳng nằm ngang như Hình 7. Tính diện tích của cửa hầm. Vận dụng 1 trang 24 Toán 12 Tập 2

Hoạt động khám phá 3 trang 24 Toán 12 Tập 2
Trong không gian, cho hình chóp O.ABCD có đáy là hình vuông cạnh a, OA ⊥ (ABCD), OA = h. Đặt trục số Ox như Hình 8. Hoạt động khám phá 3 trang 24 Toán 12 Tập 2

Thực hành 5 trang 25 Toán 12 Tập 2
Một bình chứa nước có hình dạng như Hình 11. Biết rằng khi nước trong bình có chiều cao x (dm) (0 ≤ x ≤ 4) thì mặt nước là hình vuông có cạnh như sau (dm). Tính dung tích của bình. Thực hành 5 trang 25 Toán 12 Tập 2

Hoạt động khám phá 4 trang 25 Toán 12 Tập 2
Cho D là hình phẳng giới hạn bởi đồ thị hàm số y = f(x) = 1/2.x, trục hoành và đường thẳng x = 4 (Hình 12a). Quay hình D xung quanh trục Ox thì được một khối nón, kí hiệu là N (Hình 12b). Hoạt động khám phá 4 trang 25 Toán 12 Tập 2

Thực hành 6 trang 26 Toán 12 Tập 2
Gọi D là hình phẳng giới hạn bởi đồ thị hàm số y = 1 + 1/x, trục hoành và hai đường thẳng x = 1, x = 2 (Hình 15). Thể tích khối tròn xoay tạo thành khi quay D quanh trục Ox. Thực hành 6 trang 26 Toán 12 Tập 2

Vận dụng 2 trang 27 Toán 12 Tập 2
Sử dụng tích phân, tính thể tích khối nón có bán kính đáy r và chiều cao h (Hình 16). Vận dụng 2 trang 27 Toán 12 Tập 2
Giải bài tập Bài tập cuối chương 4.

Bài 1 trang 28 Toán 12 Tập 2
Hàm số nào sau đây là một nguyên hàm của hàm số. Bài 1 trang 28 Toán 12 Tập 2

Bài 2 trang 28 Toán 12 Tập 2
Hàm số nào sau đây là một nguyên hàm của hàm số. Bài 2 trang 28 Toán 12 Tập 2
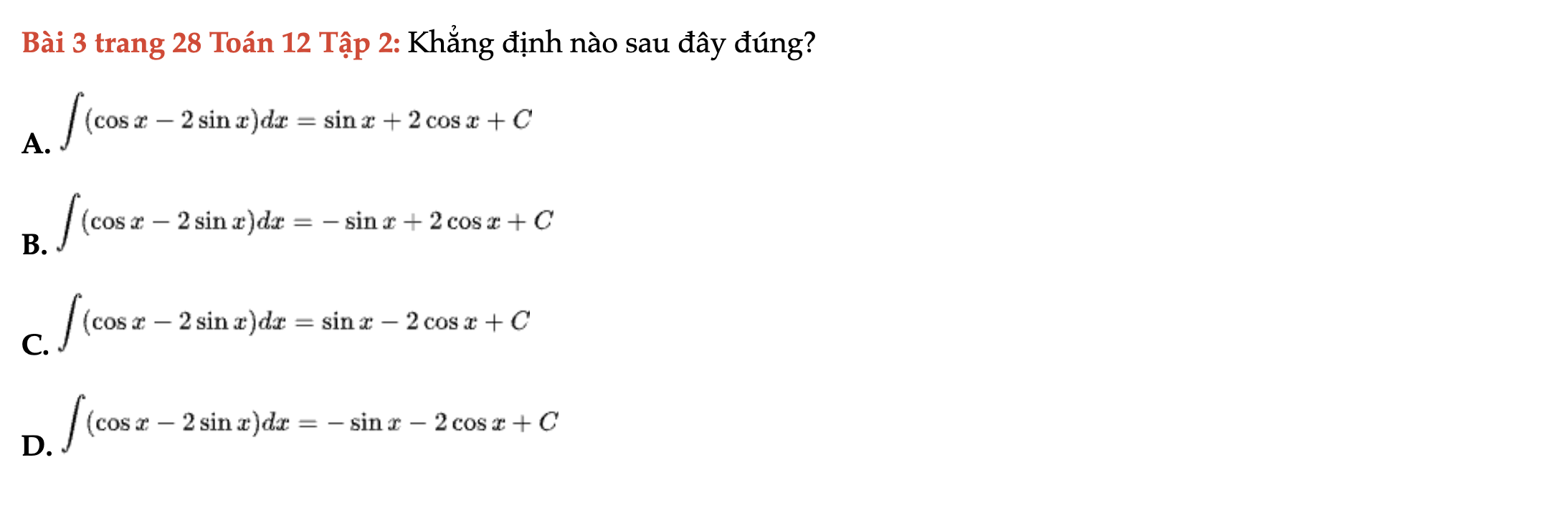
Bài 3 trang 28 Toán 12 Tập 2
Khẳng định nào sau đây đúng? Bài 3 trang 28 Toán 12 Tập 2

Bài 4 trang 28 Toán 12 Tập 2
Khẳng định nào sau đây đúng? Bài 4 trang 28 Toán 12 Tập 2

Bài 5 trang 28 Toán 12 Tập 2
Khẳng định nào sau đây đúng? Bài 5 trang 28 Toán 12 Tập 2

Bài 6 trang 28 Toán 12 Tập 2
Giá trị của biểu thức sau bằng? Bài 6 trang 28 Toán 12 Tập 2
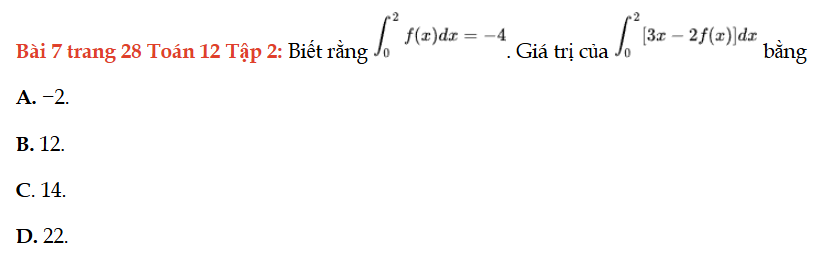
Bài 7 trang 28 Toán 12 Tập 2
Giá trị của biểu thức sau bằng. Bài 7 trang 28 Toán 12 Tập 2

Bài 8 trang 28 Toán 12 Tập 2
Giá trị của biểu thức sau bằng. Bài 8 trang 28 Toán 12 Tập 2

Bài 9 trang 28 Toán 12 Tập 2
Diện tích của hình phẳng giới hạn bởi đồ thị của hai hàm số và hai đường thẳng bằng. Bài 9 trang 28 Toán 12 Tập 2
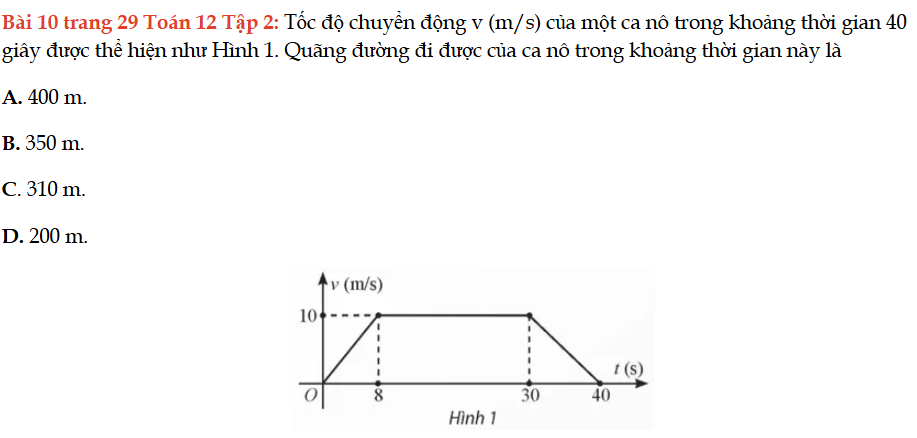
Bài 10 trang 29 Toán 12 Tập 2
Tốc độ chuyển động v (m/s) của một ca nô trong khoảng thời gian 40 giây được thể hiện như Hình 1. Quãng đường đi được của ca nô trong khoảng thời gian này là. Bài 10 trang 29 Toán 12 Tập 2

Bài 11 trang 29 Toán 12 Tập 2
Cho D là hình phẳng giới hạn bởi đồ thị hàm số, trục tung, trục hoành và đường thẳng. Thể tích của khối tròn xoay tạo thành khi quay D quanh trục hoành bằng. Bài 11 trang 29 Toán 12 Tập 2
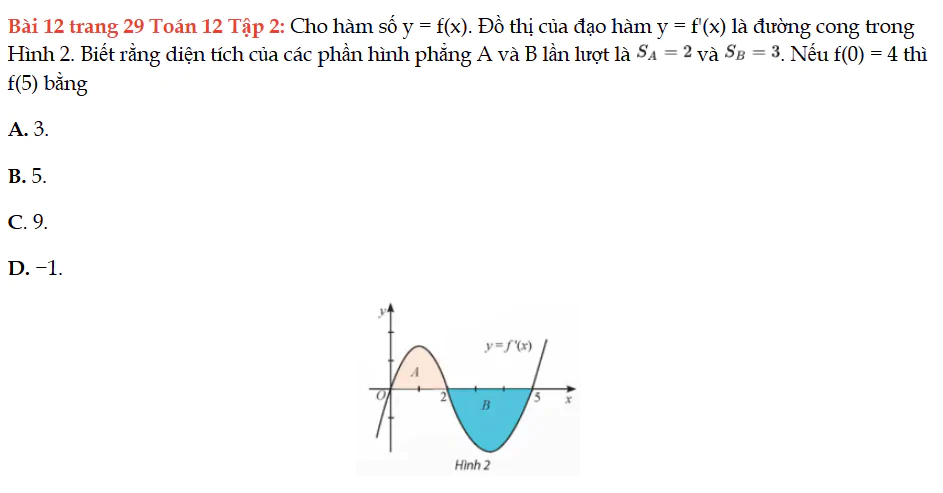
Bài 12 trang 29 Toán 12 Tập 2
Cho hàm số y = f(x). Đồ thị của đạo hàm y = f'(x) là đường cong trong Hình 2. Nếu f(0) = 4 thì f(5) bằng. Bài 12 trang 29 Toán 12 Tập 2

Bài 13 trang 29 Toán 12 Tập 2
Tìm nguyên hàm của các hàm số sau. Bài 13 trang 29 Toán 12 Tập 2
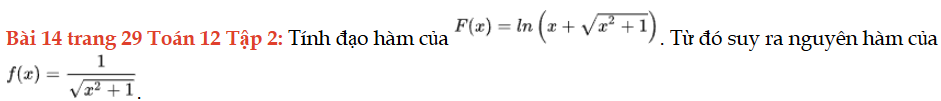
Bài 14 trang 29 Toán 12 Tập 2
Tính đạo hàm của F(x), từ đó suy ra nguyên hàm của f(x). Bài 14 trang 29 Toán 12 Tập 2
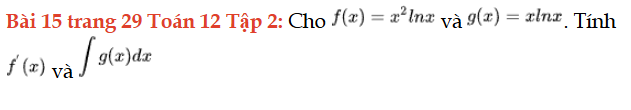
Bài 15 trang 29 Toán 12 Tập 2
Bài 15 trang 29 Toán 12 Tập 2

Bài 16 trang 29 Toán 12 Tập 2
Tính các tích phân sau. Bài 16 trang 29 Toán 12 Tập 2
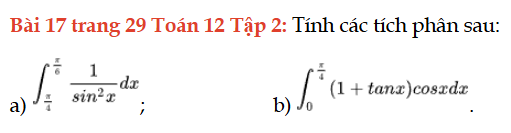
Bài 17 trang 29 Toán 12 Tập 2
Tính các tích phân sau. Bài 17 trang 29 Toán 12 Tập 2

Bài 18 trang 29 Toán 12 Tập 2
Một vật chuyển động với tốc độ v, với thời gian t tính theo giây, tính quãng đường vật đi được trong khoảng thời gian từ t = 0 đến t = 5. Bài 18 trang 29 Toán 12 Tập 2

Bài 19 trang 30 Toán 12 Tập 2
Một chất điểm đang chuyển động với tốc độ v thì tăng tốc với gia tốc không đổi a. Hỏi tốc độ của chất điểm là bao nhiêu sau 10 giây kể từ khi bắt đầu tăng tốc. Bài 19 trang 30 Toán 12 Tập 2

Bài 20 trang 30 Toán 12 Tập 2
Tốc độ tăng dân số của một thành phố trong một số năm được ước lượng bởi công thức sau. Bài 20 trang 30 Toán 12 Tập 2

Bài 21 trang 30 Toán 12 Tập 2
Sau khi được thả rơi tự do từ độ cao 100 m, một vật rơi xuống với tốc độ v(t) = 10t (m/s), trong đó t là thời gian tính theo giây kể từ khi thả vật. Bài 21 trang 30 Toán 12 Tập 2
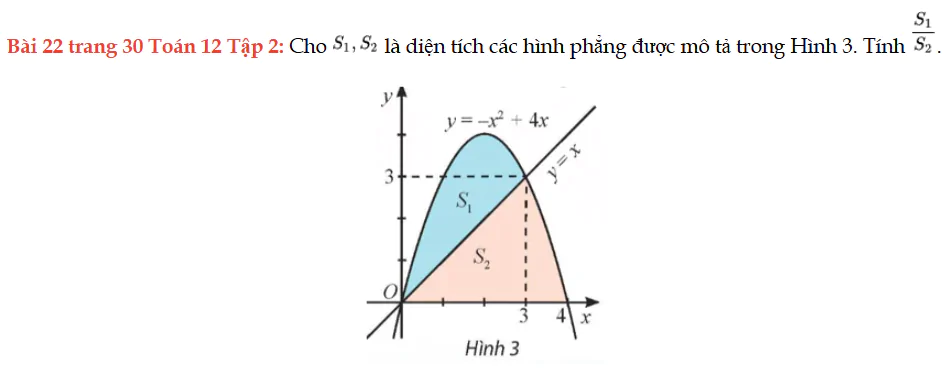
Bài 22 trang 30 Toán 12 Tập 2
Tính tỉ số diện tích các hình phẳng được mô tả trong Hình 3. Bài 22 trang 30 Toán 12 Tập 2
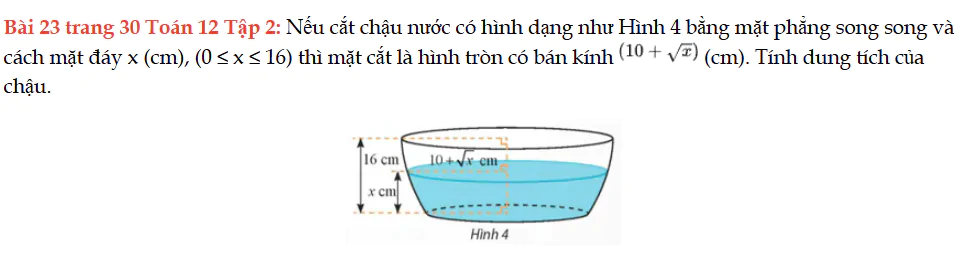
Bài 23 trang 30 Toán 12 Tập 2
Nếu cắt chậu nước có hình dạng như Hình 4 bằng mặt phẳng song song và cách mặt đáy thì mặt cắt là hình tròn có bán kính. Tính dung tích của chậu. Bài 23 trang 30 Toán 12 Tập 2
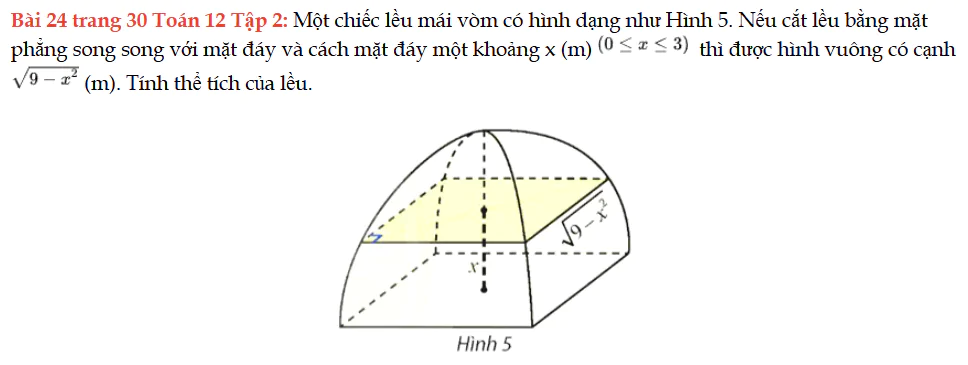
Bài 24 trang 30 Toán 12 Tập 2
Một chiếc lều mái vòm có hình dạng như Hình 5. Nếu cắt lều bằng mặt phẳng song song với mặt đáy và cách mặt đáy một khoảng x (m) thì được hình vuông có cạnh. Tính thể tích của lều. Bài 24 trang 30 Toán 12 Tập 2
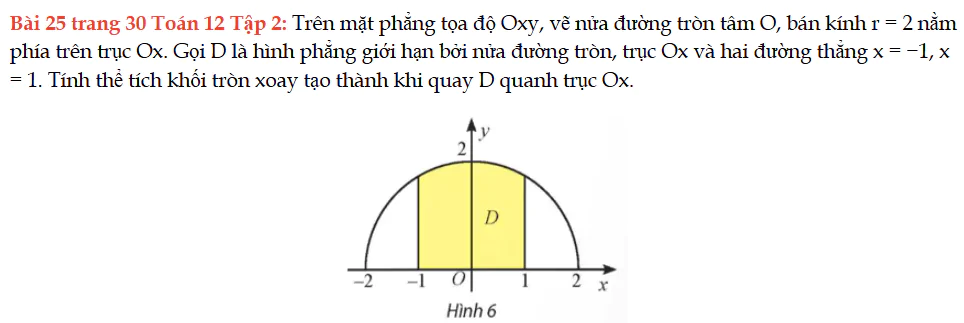
Bài 25 trang 30 Toán 12 Tập 2
Trên mặt phẳng tọa độ Oxy, vẽ nửa đường tròn tâm O, bán kính r = 2 nằm phía trên trục Ox. Gọi D là hình phẳng giới hạn bởi nửa đường tròn, trục Ox và hai đường thẳng x = −1, x = 1. Tính thể tích khối tròn xoay tạo thành khi quay D quanh trục Ox.