Giải bài tập Bài 1 trang 20 Toán 12 Tập 2 | SGK Toán 12 - Chân trời sáng tạo
Hướng dẫn giải chi tiết từng bước bài tập Bài 1 trang 20 Toán 12 Tập 2. Bài 2. Tích phân.. SGK Toán 12 - Chân trời sáng tạo
Đề bài:
Bài 1 trang 20 Toán 12 Tập 2: Tính diện tích hình thang cong giới hạn bởi
a) Đồ thị hàm số  , trục hoành và hai đường thẳng x = 0, x = 2 (Hình 7);
, trục hoành và hai đường thẳng x = 0, x = 2 (Hình 7);
b) Đồ thị hàm số  , trục hoành và hai đường thẳng x = 1, x = 3 (Hình 8).
, trục hoành và hai đường thẳng x = 1, x = 3 (Hình 8).

Đáp án và cách giải chi tiết:
a) Vì 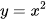 liên tục và không âm trên [0; 2] nên ta có:
liên tục và không âm trên [0; 2] nên ta có:
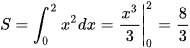
b) Vì 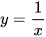 liên tục và không âm trên [1; 3] nên ta có:
liên tục và không âm trên [1; 3] nên ta có:
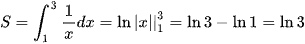
Nguồn: loigiaitoan.com
Tổng số đánh giá:
Xếp hạng: / 5 sao
Bài tập liên quan:
Bài 6 trang 20 Toán 12 Tập 2
Bài 6 trang 20 Toán 12 Tập 2: Giả sử tốc độ v (m/s) của một thang máy di chuyển từ tầng 1 lên tầng cao nhất theo thời gian t (giây) được cho bởi công thức:

Tính quãng đường chuyển động và tốc độ trung bình của thang máy.
Hoạt động khởi động trang 12 Toán 12 Tập 2
Một ô tô đang di chuyển với vận tốc 20 m/s thì hãm phanh nên tốc độ (m/s) của xe thay đổi theo thời gian t (giây) được tính theo công thức v(t) = 20 – 5t (0 ≤ t ≤ 4). Kể từ khi hãm phanh đến khi dừng, ô tô đi được quãng đường bao nhiêu?
Thực hành 1 trang 13 Toán 12 Tập 2
Tính diện tích hình thang cong giới hạn bởi đồ thị hàm số y = f(x) = ex, trục hoành, trục tung và đường thẳng x = 1 (Hình 4).

Hoạt động khám phá 2 trang 14 Toán 12 Tập 2
Cho hàm số f(x) = 2x – 1. Lấy hai nguyên hàm tùy ý F(x) và G(x) của f(x), rồi tính F(3) – F(0) và G(3) – G(0). Nhận xét về kết quả nhận được.
Vận dụng 1 trang 16 Toán 12 Tập 2
Sau khi xuất phát, ô tô di chuyển với tốc độ v(t) = 2t - 0,03t2 (0 ≤ t ≤ 10), trong đó v(t) tính theo m/s, thời gian t tính theo giây với t = 0 là thời điểm xe xuất phát.
a) Tính quãng đường xe đi được sau 5 giây, sau 10 giây.
b) Tính tốc độ trung bình của xe trong khoảng thời gian t = 0 đến t = 10.
Hoạt động khám phá 3 trang 16 Toán 12 Tập 2
a) Tìm một nguyên hàm F(x) của hàm số f(x) = 6x5. Từ đó, tính  .
.
b) Tính  .
.
c) Có nhận xét gì về giá trị của I và 6J.
Hoạt động khám phá 4 trang 17 Toán 12 Tập 2
a) Tìm một nguyên hàm F(x) của hàm số f(x) = x2 + ex. Từ đó, tính 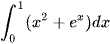 .
.
b) Tính 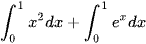 .
.
c) Có nhận xét gì về hai kết quả trên?
Vận dụng 2 trang 18 Toán 12 Tập 2
Tại một nhà máy sản xuất một loại phân bón, gọi P(x) là lợi nhuận (tính theo triệu đồng) thu được từ việc bán x tấn sản phẩm trong một tuần. Khi đó, đạo hàm P'(x), gọi là lợi nhuận cận biên, cho biết tốc độ tăng lợi nhuận theo lượng sản phẩn bán được. Giả sử lợi nhuận cận biên (tính theo triệu đồng trên tấn) của nhà máy được ước lượng bởi công thức P'(x) = 16 – 0,02x với 0 ≤ x ≤ 100. Tính lợi nhuận nhà máy thu được khi bán 90 tấn sản phẩm trong tuần. Biết rằng nhà máy lỗ 25 triệu đồng nếu không bán được lượng sản phẩm nào trong tuần.
Vận dụng 3 trang 19 Toán 12 Tập 2
Biết rằng tốc độ v (km/phút) của một ca nô cao tốc thay đổi theo thời gian t (phút) như sau: v(t) = 
Tính quãng đường ca nô di chuyển được trong khoảng thời gian từ 0 đến 20 phút.

Bài 2 trang 20 Toán 12 Tập 2
Bài 2 trang 20 Toán 12 Tập 2: Tính các tích phân sau:
a)  ; b)
; b) 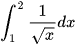 ;
;
c) 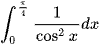 ; d)
; d) 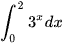 .
.
Bài 3 trang 20 Toán 12 Tập 2
Bài 3 trang 20 Toán 12 Tập 2: Tính các tích phân sau:
a)  ;
;
b)  ;
;
c) 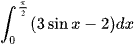 ;
;
d) 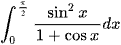 .
.
Bài 4 trang 20 Toán 12 Tập 2
Bài 4 trang 20 Toán 12 Tập 2: Tính các tích phân sau:
a)  ; b)
; b)  c)
c) 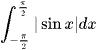 .
.
Bài 5 trang 20 Toán 12 Tập 2
Bài 5 trang 20 Toán 12 Tập 2: Mặt cắt ngang của một ống dẫn khí nóng là hình vành khuyên như Hình 9. Khí bên trong ống được duy trì ở 150°C. Biết rằng nhiệt độ T(°C) tại điểm A trên thành ống là hàm số của khoảng cách x (cm) từ A đến tâm của mặt cắt và 
(Nguồn: Y.A.Cengel, A.I.Gahjar, Heat and Mass Transfer, McGraw Hill, 2015)
Tìm nhiệt độ mặt ngoài của ống.

Hoạt động khám phá 1 trang 12 Toán 12 Tập 2
Cho hàm số y = f(x) = x + 1. Với mỗi x ≥ 1, kí hiệu S(x) là diện tích của hình thang giới hạn bởi đồ thị hàm số y = f(x), trục hoành và hai đường thẳng vuông góc với Ox tại các điểm có hoành độ 1 và x.
a) Tính S(3).
b) Tính S(x) với mỗi x ≥ 1.
c) Tính S'(x). Từ đó suy ra S(x) là một nguyên hàm của f(x) trên [1; +∞).
d) Cho F(x) là một nguyên hàm của hàm số f(x). Chứng tỏ rằng F(3) – F(1) = S(3). Từ đó nhận xét về cách tính S(3) khi biết một nguyên hàm của f(x).

Hoạt động khám phá 5 trang 18 Toán 12 Tập 2
Cho hàm số f(x) = 2x. Tính và so sánh kết quả:  và
và  .
.
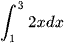 ;
;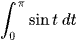 ;
;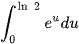 .
. ;
; ;
; .
. ;
;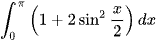 ;
; .
. ;
; ;
;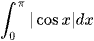 .
.