Giải bài tập Bài 3 trang 65 Toán 12 Tập 2 | SGK Toán 12 - Chân trời sáng tạo
Hướng dẫn giải chi tiết từng bước bài tập Bài 3 trang 65 Toán 12 Tập 2. Bài 3. Phương trình mặt cầu. SGK Toán 12 - Chân trời sáng tạo
Đề bài:
Bài 3 trang 65 Toán 12 Tập 2: Cho hai điểm A(1; 0; 0) và B(5; 0; 0). Chứng minh rằng nếu điểm M(x; y; z) thỏa mãn 
thì M thuộc một mặt cầu (S). Tìm tâm và bán kính của (S).
Đáp án và cách giải chi tiết:
Ta có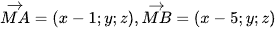 
.
Có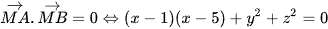 
.
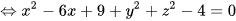
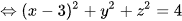Do đó M luôn thuộc mặt cầu tâm I(3; 0; 0) và R = 2.
Nguồn: loigiaitoan.com
Tổng số đánh giá:
Xếp hạng: / 5 sao
Bài tập liên quan:
Bài 1 trang 65 Toán 12 Tập 2
Bài 1 trang 65 Toán 12 Tập 2: Viết phương trình mặt cầu (S):
a) Có tâm I(7; −3; 0), bán kính R = 8;
b) Có tâm M(3; 1; −4) và đi qua điểm N(1; 0; 1);
c) Có đường kính AB với A(4; 6; 8) và B(2; 4; 4).
Bài 2 trang 65 Toán 12 Tập 2
Bài 2 trang 65 Toán 12 Tập 2: Trong các phương trình sau, phương trình nào là phương trình mặt cầu? Xác định tâm và bán kính của mặt cầu đó.
a)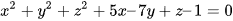 
;
b) 
;
c) 
.
Bài 4 trang 65 Toán 12 Tập 2
Bài 4 trang 65 Toán 12 Tập 2: Phần mềm mô phỏng thiết bị thám hiểm đại dương có dạng hình cầu trong không gian Oxyz. Cho biết tọa độ tâm mặt cầu là I(360; 200; 400) và bán kính r = 2 m. Viết phương trình mặt cầu.
Bài 5 trang 65 Toán 12 Tập 2
Bài 5 trang 65 Toán 12 Tập 2: Người ta muốn thiết kế một bồn chứa khí hóa lỏng hình cầu bằng phần mềm 3D. Cho biết phương trình bề mặt của bồn chứa là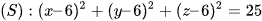 
. Phương trình mặt phẳng chứa nắp là 
.
a) Tìm tâm và bán kính của bồn chứa.
b) Tính khoảng cách từ tâm bồn chứa đến mặt phẳng chứa nắp.
Hoạt động khởi động trang 61 Toán 12 Tập 2
Ta đã biết trong mặt phẳng tọa độ Oxy, phương trình đường tròn tâm I(a; b), bán kính R có dạng: (x – a)2 + (y – b)2 = R2.
Trong không gian Oxyz, phương trình mặt cầu có dạng như thế nào?
Hoạt động khám phá 1 trang 61 Toán 12 Tập 2
Trong không gian Oxyz, cho mặt cầu S(I; R) có tâm I(a; b; c) và bán kính R. Xét một điểm M(x; y; z) thay đổi.
a) Tính khoảng cách IM theo x, y, z và a, b, c.
b) Nêu điều kiện cần và đủ của x, y, z để điểm M(x; y; z) nằm trên mặt cầu S(I; R).
Thực hành 1 trang 62 Toán 12 Tập 2
Viết phương trình mặt cầu (S):
a) Có tâm I(3; −2; −4), bán kính R = 10;
b) Có đường kính EF với E(3; −1; 8) và F(7; −3; 0);
c) Có tâm M(−2; 1; 3) và đi qua điểm N(2; −3; −4).
Vận dụng 1 trang 62 Toán 12 Tập 2
Trong không gian Oxyz (đơn vị của các trục tọa độ là mét), các nhà nghiên cứu khí tượng dùng một phần mềm mô phỏng bề mặt của một quả bóng thám không có dạng hình cầu bằng phương trình (x – 300)2 + (y – 400)2 + (z – 2000)2 = 1. Tìm tọa độ tâm, bán kính của quả bóng và tính khoảng cách từ tâm của quả bóng đến mặt đất có phương trình z = 0.
Hoạt động khám phá 2 trang 63 Toán 12 Tập 2
a) Trong không gian Oxyz, cho điểm M(x; y; z) thay đổi có tọa độ luôn thỏa mãn phương trình x2 + y2 + z2 – 2x – 4y – 6z – 11 = 0. (*)
i) Biến đổi (*) về dạng: (x – 1)2 + (y – 2)2 + (z – 3)2 = 25.
ii) Chứng tỏ M(x; y; z) luôn thuộc mặt cầu (S). Tìm tâm và bán kính của (S).
b) Bằng cách biến đổi phương trình x2 + y2 + z2 – 2x – 4y – 6z + 15 = 0 (**) về dạng (x – 1)2 + (y – 2)2 + (z – 3)2 = −1, hãy cho biết phương trình (**) có thể là phương trình mặt cầu hay không?
Thực hành 2 trang 63 Toán 12 Tập 2
Trong các phương trình sau, phương trình nào là phương trình mặt cầu? Xác định tâm và bán kính của mặt cầu đó.
a) x2 + y2 + z2 + 4z – 32 = 0;
b) x2 + y2 + z2 + 2x + 2y – 2z + 4 = 0
Vận dụng 2 trang 64 Toán 12 Tập 2
Bề mặt của một bóng thám không dạng hình cầu có phương trình x2 + y2 + z2 – 200x – 600y – 4000z + 4099900 = 0. Tìm tọa độ tâm và bán kính mặt cầu.
Vận dụng 3 trang 64 Toán 12 Tập 2
Đầu in phun của một máy in 3D đang in bề mặt của một mặt cầu có phương trình 
. Tính khoảng cách từ đầu in phun đến tâm mặt cầu.
