Giải bài tập Hoạt động khám phá 3 trang 46 Toán 12 Tập 2 | SGK Toán 12 - Chân trời sáng tạo
Hướng dẫn giải chi tiết từng bước bài tập Hoạt động khám phá 3 trang 46 Toán 12 Tập 2. Bài 2. Phương trình đường thẳng trong không gian. SGK Toán 12 - Chân trời sáng tạo
Đề bài:
Cho đường thẳng d có phương trình tham số  với a1, a2, a3 đều khác 0.
với a1, a2, a3 đều khác 0.
Lấy điểm M(x; y; z) bất kì thuộc d. So sánh các biểu thức:  .
.
Đáp án và cách giải chi tiết:
Ta có 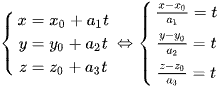 .
.
Mà M ∈ d nên 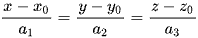 .
.
Nguồn: loigiaitoan.com
Tổng số đánh giá:
Xếp hạng: / 5 sao
Bài tập liên quan:
Bài 1 trang 59 Toán 12 Tập 2
Bài 1 trang 59 Toán 12 Tập 2: Viết phương trình tham số của đường thẳng a trong mỗi trường hợp sau:
a) Đường thẳng a đi qua điểm  và có vectơ chỉ phương
và có vectơ chỉ phương  .
.
b) Đường thẳng a đi qua hai điểm  và
và  .
.
Bài 2 trang 59 Toán 12 Tập 2
Bài 2 trang 59 Toán 12 Tập 2: Viết phương trình chính tắc của đường thẳng b trong mỗi trường hợp sau:
a) Đường thẳng b đi qua điểm  và có vectơ chỉ phương
và có vectơ chỉ phương  .
.
b) Đường thẳng b đi qua hai điểm  và
và 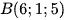 .
.
Bài 3 trang 59 Toán 12 Tập 2
Bài 3 trang 59 Toán 12 Tập 2: Cho đường thẳng d có phương trình chính tắc  .
.
a) Tìm một vectơ chỉ phương của d và một điểm trên d.
b) Viết phương trình tham số của d.
Bài 4 trang 59 Toán 12 Tập 2
Bài 4 trang 59 Toán 12 Tập 2: Trong trò chơi mô phỏng bắn súng 3D trong không gian Oxyz, một xạ thủ đang ngắm với tọa độ khe ngắm và đầu ruồi lần lượt là  . Viết phương trình tham số của đường ngắm bắn của xạ thủ (xem như đường thẳng MN).
. Viết phương trình tham số của đường ngắm bắn của xạ thủ (xem như đường thẳng MN).

Bài 5 trang 60 Toán 12 Tập 2
Bài 5 trang 60 Toán 12 Tập 2: Xét vị trí tương đối giữa các cặp đường thẳng sau:
a)  và
và 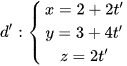
b)  và
và  .
.
Bài 6 trang 60 Toán 12 Tập 2
Bài 6 trang 60 Toán 12 Tập 2: Viết phương trình tham số của đường thẳng d đi qua điểm 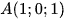 và song song với đường thẳng
và song song với đường thẳng 
Bài 7 trang 60 Toán 12 Tập 2
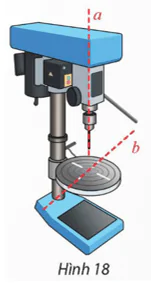
Bài 7 trang 60 Toán 12 Tập 2: Trên phần mềm mô phỏng 3D một máy khoan trong không gian Oxyz, cho biết phương trình trục a của mũi khoan và một đường rãnh b trên vật cần khoan (Hình 18) lần lượt là:
 và
và 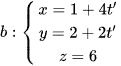
a) Chứng minh a, b vuông góc và cắt nhau.
b) Tìm giao điểm của a và b.
Bài 8 trang 60 Toán 12 Tập 2
Bài 8 trang 60 Toán 12 Tập 2: Tính góc giữa hai đường thẳng  và
và  .
.
Bài 9 trang 60 Toán 12 Tập 2
Bài 9 trang 60 Toán 12 Tập 2: Tính góc giữa đường thẳng  và mặt phẳng
và mặt phẳng  .
.
Bài 10 trang 60 Toán 12 Tập 2
Bài 10 trang 60 Toán 12 Tập 2: Tính góc giữa hai mặt phẳng 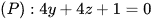 và
và  .
.
Bài 12 trang 60 Toán 12 Tập 2
Bài 12 trang 60 Toán 12 Tập 2: Trong không gian Oxyz, cho hình lăng trụ đứng OBC.O'B'C' có đáy là tam giác OBC vuông tại O. Cho biết B(3; 0; 0), C(0; 1; 0), O'(0; 0; 2). Tính góc giữa:
a) Hai đường thẳng BO' và B'C;
b) Hai mặt phẳng (O'BC) và (OBC);
c) Đường thẳng B'C và mặt phẳng (O'BC)
Bài 11 trang 60 Toán 12 Tập 2
Bài 11 trang 60 Toán 12 Tập 2: Trên một cánh đồng điện mặt trời, người ta đã thiết lập sẵn một hệ tọa độ Oxyz. Hai tấm pin năng lượng lần lượt nằm trong hai mặt phẳng  và
và  .
.
a) Tính góc giữa (P) và (P').
b) Tính góc hợp bởi (P) và (P') với mặt đất (Q) có phương trình z = 0.

Hoạt động khởi động trang 43 Toán 12 Tập 2
Ta đã biết trong mặt phẳng Oxy, phương trình tham số của đường thẳng có dạng: 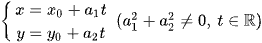 .
.
Trong không gian Oxyz, phương trình tham số của đường thẳng có dạng như thế nào?

Hoạt động khám phá 1 trang 44 Toán 12 Tập 2
Trong không gian Oxyz, cho điểm M0 cố định và vectơ  khác
khác  . Có bao nhiêu đường thẳng d đi qua M0 và song song hoặc trùng với giá của
. Có bao nhiêu đường thẳng d đi qua M0 và song song hoặc trùng với giá của  ?
?

Thực hành 1 trang 44 Toán 12 Tập 2
Trong không gian Oxyz, cho hình lăng trụ tam giác ABC.A'B'C' với A(1; 2; 1), B(7; 5; 3), C(4; 2; 0), A'(4; 9; 9). Tìm tọa độ một vectơ chỉ phương của mỗi đường thẳng AB, A'C' và BB'.
Hoạt động khám phá 2 trang 44 Toán 12 Tập 2
Trong không gian Oxyz, cho đường thẳng d đi qua điểm M0(x0; y0; z0) cố định và có vectơ chỉ phương là  khác
khác  .
.
a) Giải thích tại sao ta có thể viết: M ∈ d ⇔  .
.
b) Với M(x; y; z) thuộc d, hãy tính x, y, z theo x0, y0, z0 và a1, a2, a3.

Thực hành 2 trang 46 Toán 12 Tập 2
Cho đường thẳng d có phương trình tham số  .
.
a) Tìm hai vectơ chỉ phương của d.
b) Tìm ba điểm trên d.
Thực hành 3 trang 46 Toán 12 Tập 2
Viết phương trình tham số của đường thẳng d đi qua điểm A(5; 0; −7) và nhận 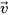 = (9; 0; -2) làm vectơ chỉ phương. Đường thẳng d có đi qua điểm M(−4; 0; −5) không?
= (9; 0; -2) làm vectơ chỉ phương. Đường thẳng d có đi qua điểm M(−4; 0; −5) không?
Thực hành 4 trang 46 Toán 12 Tập 2
Viết phương trình chính tắc của đường thẳng d đi qua điểm M0(5; 0; −6) và nhận  = (3; 2; -4) làm vectơ chỉ phương.
= (3; 2; -4) làm vectơ chỉ phương.
Hoạt động khám phá 4 trang 47 Toán 12 Tập 2
Cho đường thẳng d đi qua hai điểm A(2; 2; 1) và B(4; 5; 3).
a) Tìm một vectơ chỉ phương của d.
b) Viết phương trình tham số và phương trình chính tắc của d.