Giải bài tập Toán 12 Chương 4. Nguyên hàm. Tích phân | Cánh Diều
Hướng dẫn giải Chương 4. Nguyên hàm. Tích phân. Nguyên hàm của một số hàm số sơ cấp. Ứng dụng hình học của tích phân.
Giải bài tập Bài 1. Nguyên hàm.

Bài 1 trang 7 Toán 12 Tập 2
Cho hàm số, tìm đạo hàm. Bài 1 trang 7 Toán 12 Tập 2

Bài 2 trang 7 Toán 12 Tập 2
Tìm nguyên hàm các hàm số. Bài 2 trang 7 Toán 12 Tập 2
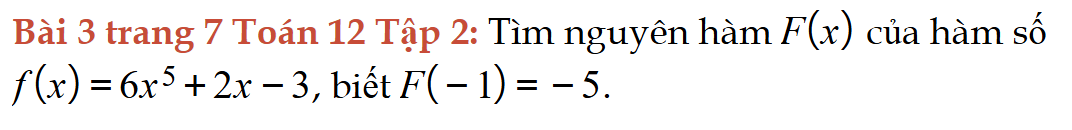
Bài 3 trang 7 Toán 12 Tập 2
Cho hàm số, tìm nguyên hàm. Bài 3 trang 7 Toán 12 Tập 2

Bài 4 trang 8 Toán 12 Tập 2
cho hàm số, tìm nguyên hàm. Bài 4 trang 8 Toán 12 Tập 2

Bài 5 trang 8 Toán 12 Tập 2
Cho hàm số, tìm nguyên hàm. Bài 5 trang 8 Toán 12 Tập 2

Bài 6 trang 8 Toán 12 Tập 2
Cho hàm số, tìm nguyên hàm. Bài 6 trang 8 Toán 12 Tập 2

Câu hỏi khởi động trang 3 Toán 12 Tập 2
Một hòn đá rơi từ mỏm đá có độ cao 150 m so với mặt đất theo phương thẳng đứng. Biết tốc độ rơi của hòn đá (tính theo đơn vị m/s) tại thời điểm t (tính theo giây) được cho bởi công thức v(t) = 9,8t. Câu hỏi khởi động trang 3 Toán 12 Tập 2
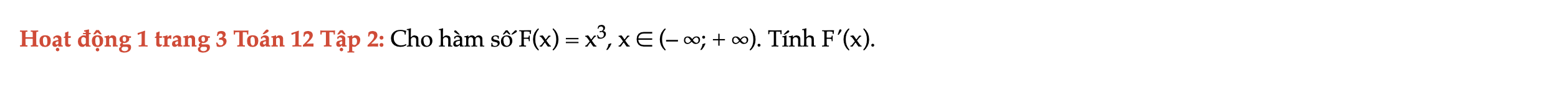
Hoạt động 1 trang 3 Toán 12 Tập 2
Cho hàm số F(x) = x3, x ∈ (– ∞; + ∞). Tính F'(x). Hoạt động 1 trang 3 Toán 12 Tập 2
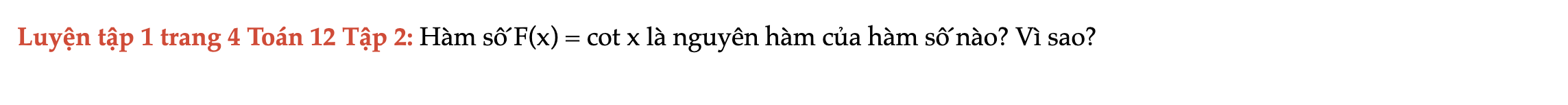
Luyện tập 1 trang 4 Toán 12 Tập 2
Hàm số F(x) = cot x là nguyên hàm của hàm số nào? Vì sao? Luyện tập 1 trang 4 Toán 12 Tập 2

Hoạt động 2 trang 4 Toán 12 Tập 2
Cho hàm số F(x) = x3 – 1, x ∈ ℝ và G(x) = x3 + 5, x ∈ ℝ. Cả hai hàm số F(x) và G(x) có phải là nguyên hàm của hàm số f(x) = 3x2 trên ℝ hay không? Hoạt động 2 trang 4 Toán 12 Tập 2

Luyện tập 2 trang 4 Toán 12 Tập 2
Tìm tất cả các nguyên hàm của hàm số f(x) = cos x trên ℝ. Luyện tập 2 trang 4 Toán 12 Tập 2
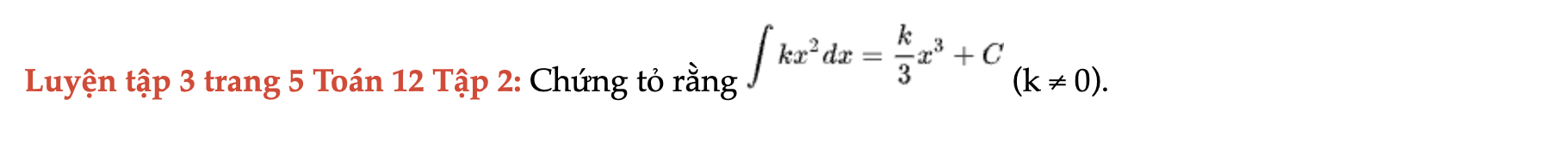
Luyện tập 3 trang 5 Toán 12 Tập 2
Luyện tập 3 trang 5 Toán 12 Tập 2
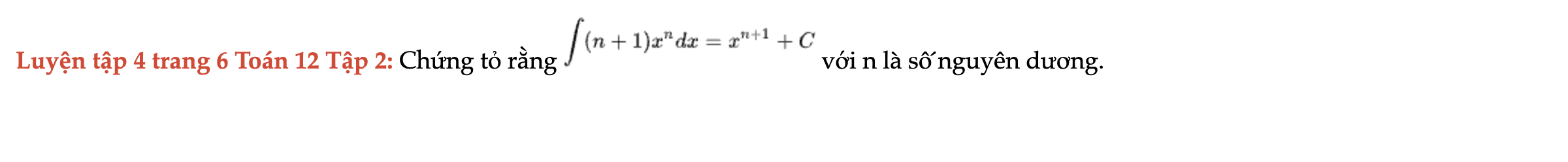
Luyện tập 4 trang 6 Toán 12 Tập 2
Luyện tập 4 trang 6 Toán 12 Tập 2

Hoạt động 3 trang 5 Toán 12 Tập 2
Cho f(x) là hàm số liên tục trên K, k là hằng số thực khác 0. Giả sử F(x) là một nguyên hàm của hàm số f(x) trên K. Hỏi kF(x) có phải là nguyên hàm của hàm số kf(x) trên K hay không? Hoạt động 3 trang 5 Toán 12 Tập 2

Hoạt động 4 trang 6 Toán 12 Tập 2
Cho f(x), g(x) là hai hàm số liên tục trên K. Giả sử F(x), G(x) lần lượt là nguyên hàm của các hàm số f(x), g(x) trên K. Hỏi F(x) + G(x) có phải là nguyên hàm của hàm số f(x) + g(x) trên K hay không? Hoạt động 4 trang 6 Toán 12 Tập 2
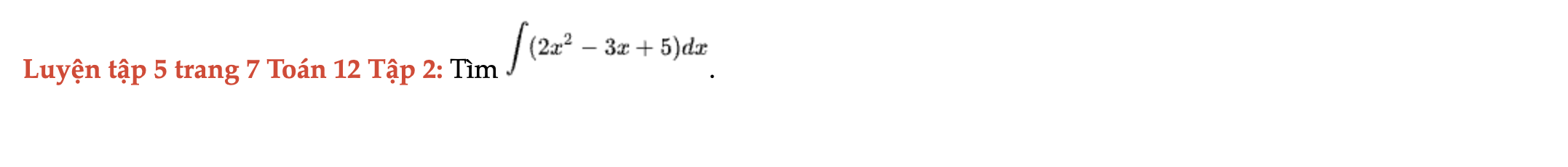
Luyện tập 5 trang 7 Toán 12 Tập 2
Luyện tập 5 trang 7 Toán 12 Tập 2
Giải bài tập Bài 2. Nguyên hàm của một số hàm số sơ cấp.

Bài 1 trang 15 Toán 12 Tập 2
Cho hàm số, tìm nguyên hàm.Bài 1 trang 15 Toán 12 Tập 2

Bài 2 trang 15 Toán 12 Tập 2
Tính nguyên hàm. Bài 2 trang 15 Toán 12 Tập 2

Bài 3 trang 15 Toán 12 Tập 2
Tính nguyên hàm. Bài 3 trang 15 Toán 12 Tập 2

Bài 4 trang 16 Toán 12 Tập 2
Tính nguyên hàm. Bài 4 trang 16 Toán 12 Tập 2

Bài 5 trang 16 Toán 12 Tập 2
Tính nguyên hàm. Bài 5 trang 16 Toán 12 Tập 2

Bài 6 trang 16 Toán 12 Tập 2
Tính nguyên hàm. Bài 6 trang 16 Toán 12 Tập 2

Bài 7 trang 16 Toán 12 Tập 2
Tính nguyên hàm. Bài 7 trang 16 Toán 12 Tập 2

Bài 8 trang 16 Toán 12 Tập 2
Tính nguyên hàm. Bài 8 trang 16 Toán 12 Tập 2

Câu hỏi khởi động trang 9 Toán 12 Tập 2
Một con lắc lò xo dao động điều hòa theo phương ngang trên mặt phẳng không ma sát như Hình 1, có vận tốc tức thời cho bởi v(t) = 4 cos t, trong đó t tính bằng giây và v(t) tính bằng centimét/giây. Câu hỏi khởi động trang 9 Toán 12 Tập 2

Hoạt động 1 trang 9 Toán 12 Tập 2
Hàm số F(x) = 1/2.x^2 có là nguyên hàm của hàm số f(x) = x hay không? Hoạt động 1 trang 9 Toán 12 Tập 2
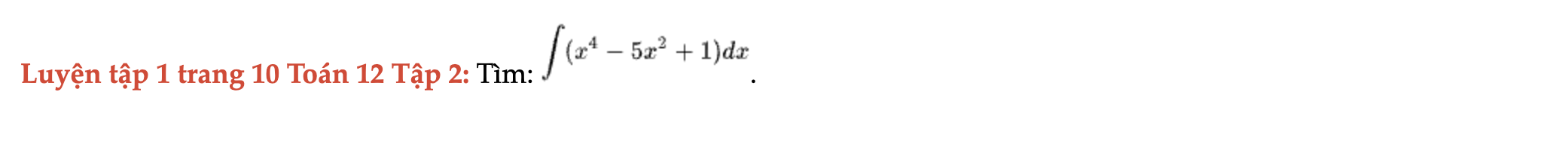
Luyện tập 1 trang 10 Toán 12 Tập 2
Luyện tập 1 trang 10 Toán 12 Tập 2

Luyện tập 2 trang 10 Toán 12 Tập 2
Luyện tập 2 trang 10 Toán 12 Tập 2
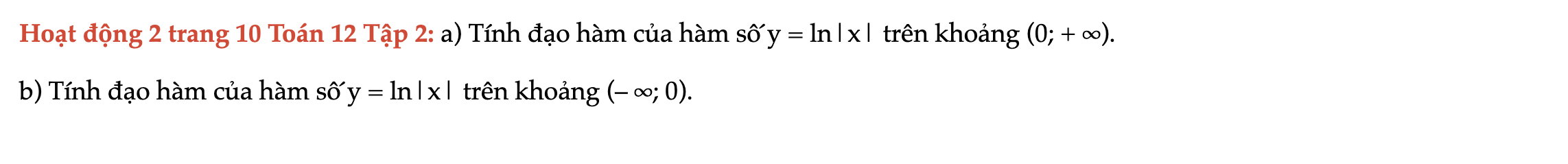
Hoạt động 2 trang 10 Toán 12 Tập 2
Tính đạo hàm của hàm số y = ln|x| trên khoảng (0; + ∞). Tính đạo hàm của hàm số y = ln|x| trên khoảng (– ∞; 0). Hoạt động 2 trang 10 Toán 12 Tập 2

Luyện tập 3 trang 10 Toán 12 Tập 2
Luyện tập 3 trang 10 Toán 12 Tập 2

Hoạt động 3 trang 11 Toán 12 Tập 2
Hàm số y = – cos x có là nguyên hàm của hàm số y = sin x hay không? Hàm số y = sin x có là nguyên hàm của hàm số y = cos x hay không? Hoạt động 3 trang 11 Toán 12 Tập 2

Luyện tập 4 trang 11 Toán 12 Tập 2
Luyện tập 4 trang 11 Toán 12 Tập 2

Luyện tập 5 trang 11 Toán 12 Tập 2
Luyện tập 5 trang 11 Toán 12 Tập 2
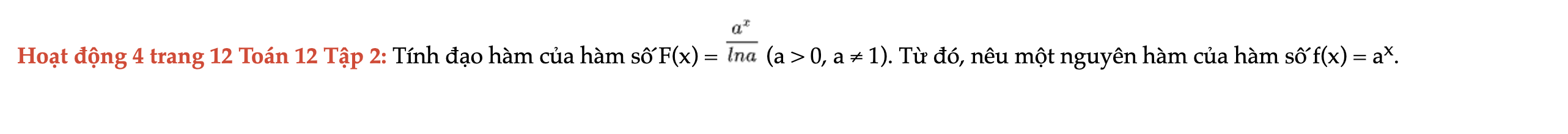
Hoạt động 4 trang 12 Toán 12 Tập 2
Tính đạo hàm của hàm số F(x) (a > 0, a ≠ 1). Từ đó, nêu một nguyên hàm của hàm số f(x) = a^x. Hoạt động 4 trang 12 Toán 12 Tập 2

Luyện tập 6 trang 12 Toán 12 Tập 2
Luyện tập 6 trang 12 Toán 12 Tập 2
Giải bài tập Bài 3. Tích phân.

Bài 1 trang 26 Tán 12 Tập 2
Tính tích phân. Bài 1 trang 26 Tán 12 Tập 2
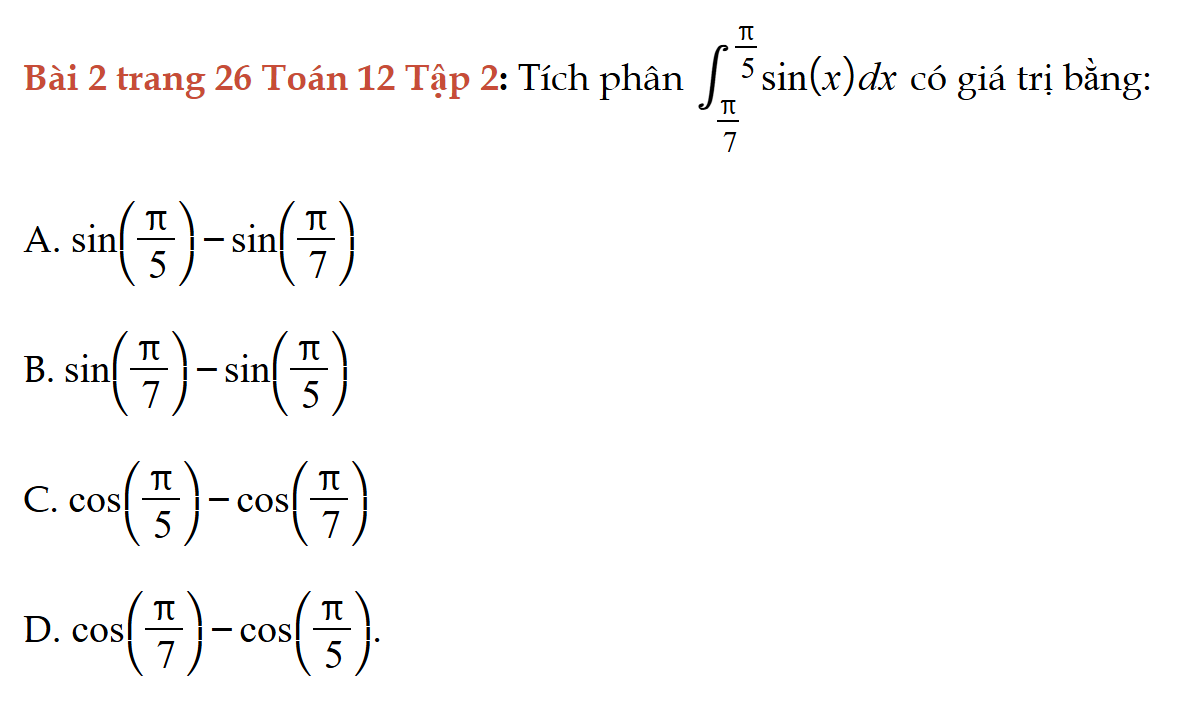
Bài 2 trang 26 Toán 12 Tập 2
Tính tích phân, Bài 2 trang 26 Toán 12 Tập 2

Bài 3 trang 26 Toán 12 Tập 2
Tính tích phân. Bài 3 trang 26 Toán 12 Tập 2
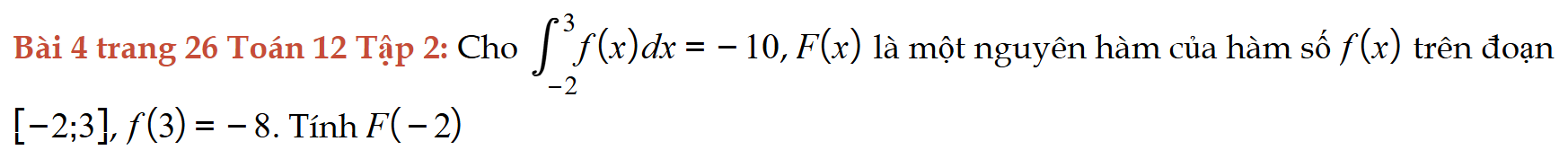
Bài 4 trang 26 Toán 12 Tập 2
Cho nguyên hàm, áp dụng tích phân tính giá trị hàm số tại một giá trị. Bài 4 trang 26 Toán 12 Tập 2
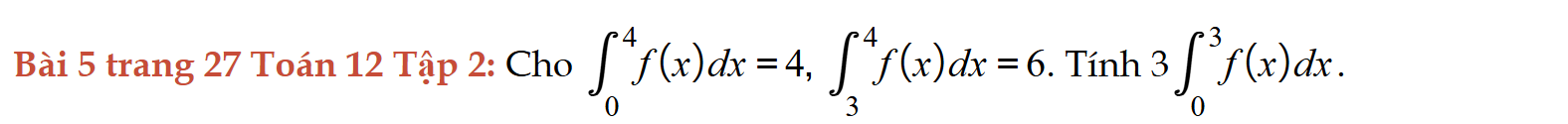
Bài 5 trang 27 Toán 12 Tập 2
Tính tích phân, Bài 5 trang 27 Toán 12 Tập 2

bài 6 trang 27 Toán 12 Tập 2
Tính tích phân. bài 6 trang 27 Toán 12 Tập 2.

Bài 7 trang 27 Toán 12 Tập 2
tính nguyên hàm, tích phân. Bài 7 trang 27 Toán 12 Tập 2
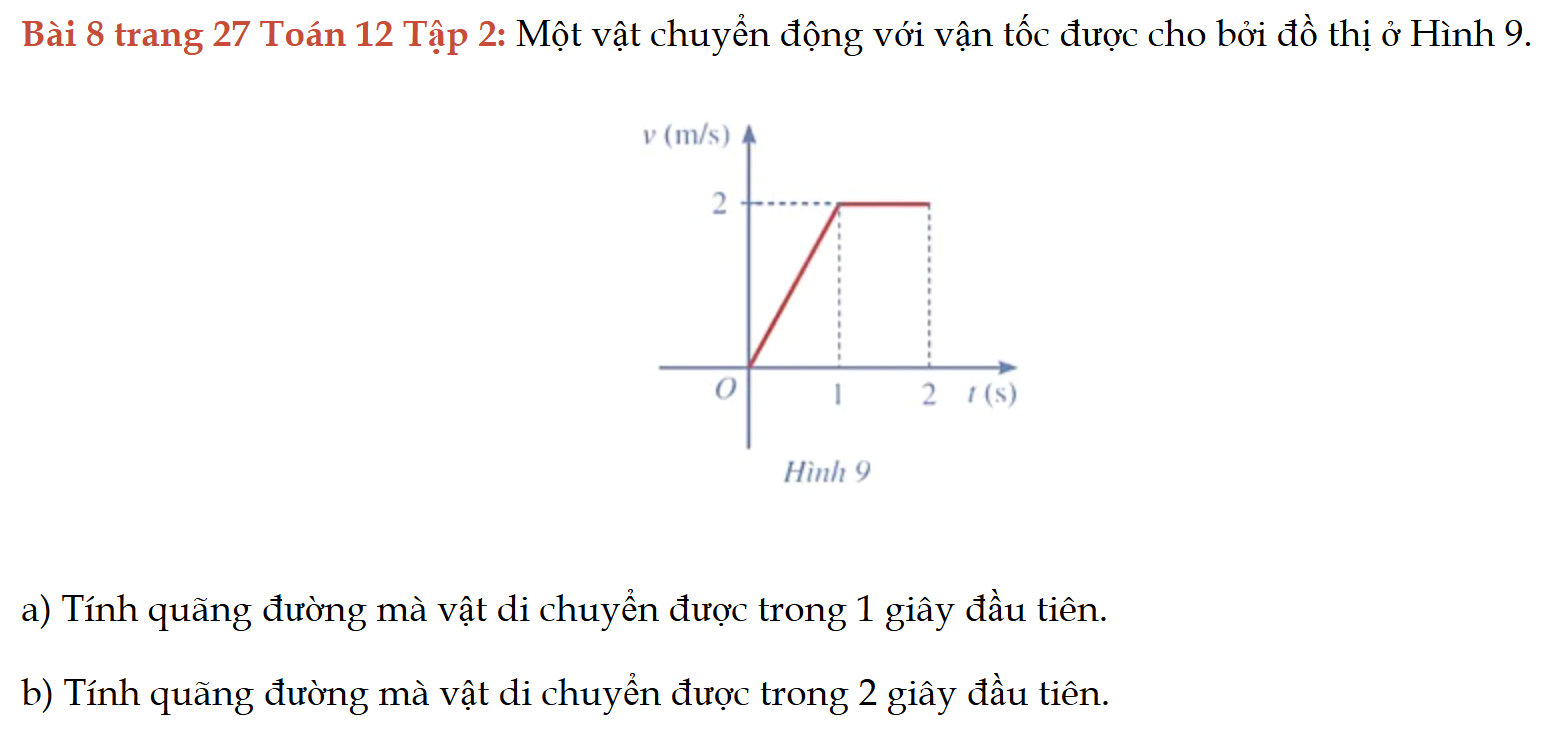
Bài 8 trang 27 Toán 12 Tập 2
Cho đồ thị hàm số, viết hàm số, tính tích phân.Bài 8 trang 27 Toán 12 Tập 2

Bài 9 trang 27 Toán 12 Tập 2
Cho hàm số, tính đạo hàm. Bài 9 trang 27 Toán 12 Tập 2

Câu hỏi khởi động trang 17 Toán 12 Tập 2
Họa sĩ thiết kế logo hình con cá cho một doanh nghiệp kinh doanh hải sản. Logo là hình phẳng giới hạn bởi hai parabol với các kích thước được cho trong Hình 3 (đơn vị trên mỗi trục tọa độ là decimét). Câu hỏi khởi động trang 17 Toán 12 Tập 2

Hoạt động 1 trang 17 Toán 12 Tập 2
Cho hàm số y = f(x) = x^2. Xét hình phẳng (được tô màu) gồm tất cả các điểm M(x; y) trên mặt phẳng tọa độ sao cho 1 ≤ x ≤ 2 và 0 ≤ y ≤ x2 (Hình 4). Hoạt động 1 trang 17 Toán 12 Tập 2

Luyện tập 1 trang 19 Toán 12 Tập 2
Cho đồ thị hàm số y = f(x) = 2x (x ∈ [0; 2]). Xét tam giác vuông OAB giới hạn bởi đồ thị của hàm số f(x) = 2x, trục Ox và đường thẳng x = 2. Luyện tập 1 trang 19 Toán 12 Tập 2

Hoạt động 2 trang 20 Toán 12 Tập 2
Cho hàm số f(x). Chứng tỏ F(x), G(x) là các nguyên hàm của hàm số f(x). Chứng minh rằng F(b) – F(a) = G(b) – G(a), tức là hiệu số F(b) – F(a) không phụ thuộc việc chọn nguyên hàm. Hoạt động 2 trang 20 Toán 12 Tập 2

Luyện tập 2 trang 20 Toán 12 Tập 2
Tính tích phân sau. Luyện tập 2 trang 20 Toán 12 Tập 2
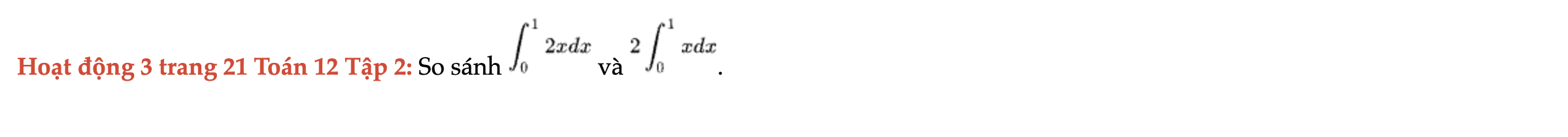
Hoạt động 3 trang 21 Toán 12 Tập 2
So sánh 2 tích phân sau. Hoạt động 3 trang 21 Toán 12 Tập 2
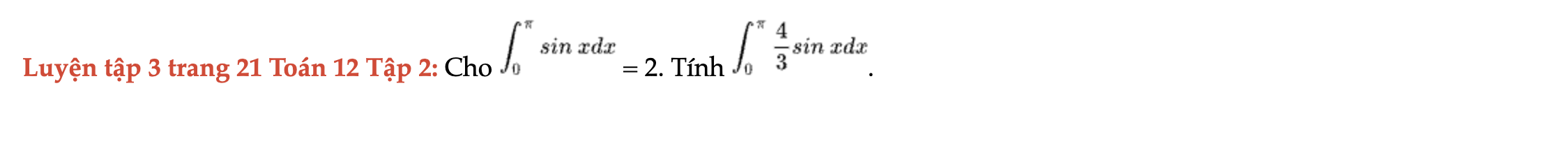
Luyện tập 3 trang 21 Toán 12 Tập 2
Luyện tập 3 trang 21 Toán 12 Tập 2

Hoạt động 4 trang 21 Toán 12 Tập 2
Hoạt động 4 trang 21 Toán 12 Tập 2
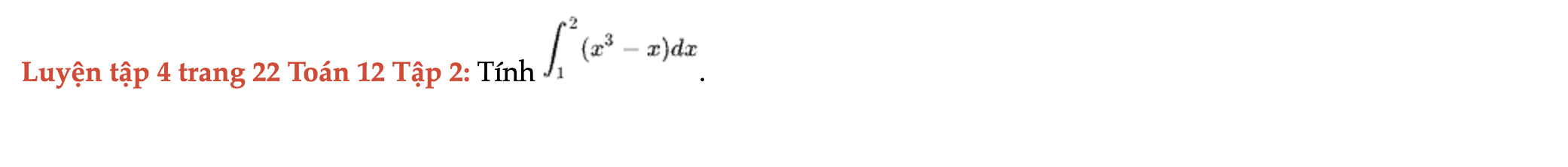
Luyện tập 4 trang 22 Toán 12 Tập 2
Tính tích phân sau. Luyện tập 4 trang 22 Toán 12 Tập 2
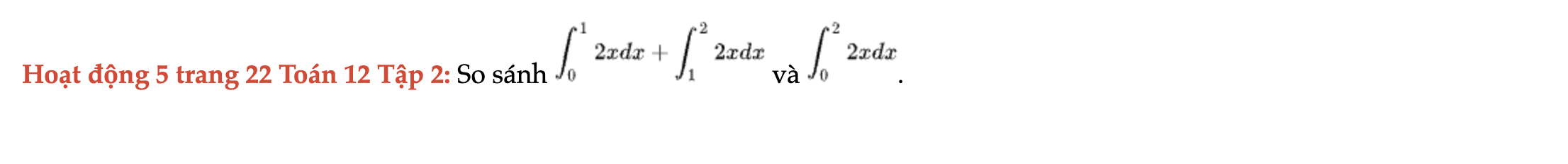
Hoạt động 5 trang 22 Toán 12 Tập 2
Hoạt động 5 trang 22 Toán 12 Tập 2

Luyện tập 5 trang 22 Toán 12 Tập 2
Luyện tập 5 trang 22 Toán 12 Tập 2

Luyện tập 6 trang 23 Toán 12 Tập 2
Tính các tích phân sau. Luyện tập 6 trang 23 Toán 12 Tập 2

Luyện tập 7 trang 23 Toán 12 Tập 2
Luyện tập 7 trang 23 Toán 12 Tập 2

Luyện tập 8 trang 24 Toán 12 Tập 2
Luyện tập 8 trang 24 Toán 12 Tập 2

Luyện tập 9 trang 25 Toán 12 Tập 2
Luyện tập 9 trang 25 Toán 12 Tập 2
Giải bài tập Bài 4. Ứng dụng hình học của tích phân.
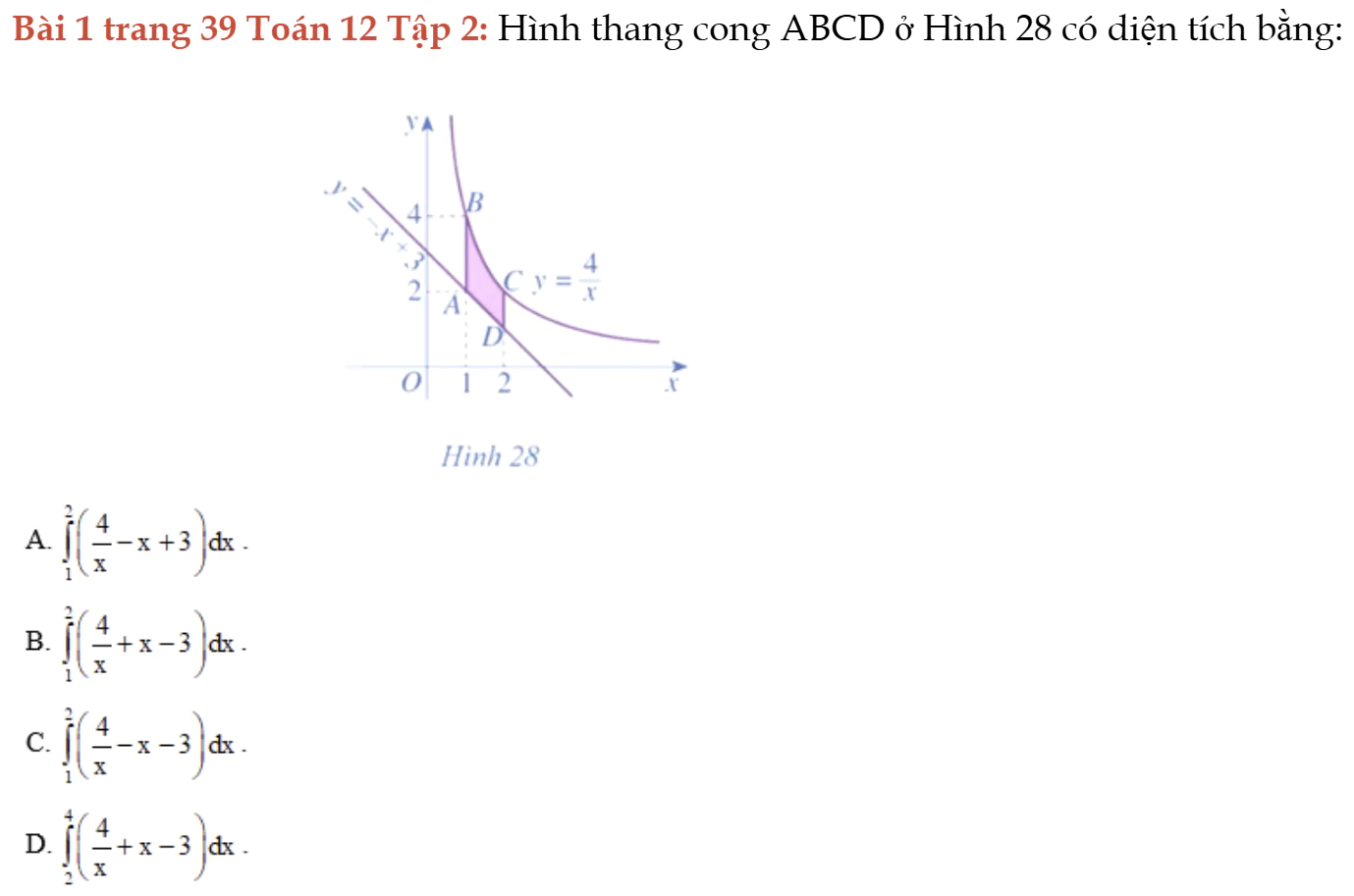
Bài 1 trang 39 Toán 12 Tập 2
Cho hai đồ thị hàm số, tìm diện tích hình được giới hạn bởi hai đồ thị. Bài 1 trang 39 Toán 12 Tập 2

Bài 2 trang 39 Toán 12 Tập 2
Cho đồ thị hàm số, đường thẳng, tính thể tích khối tròn xoay . Bài 2 trang 39 Toán 12 Tập 2
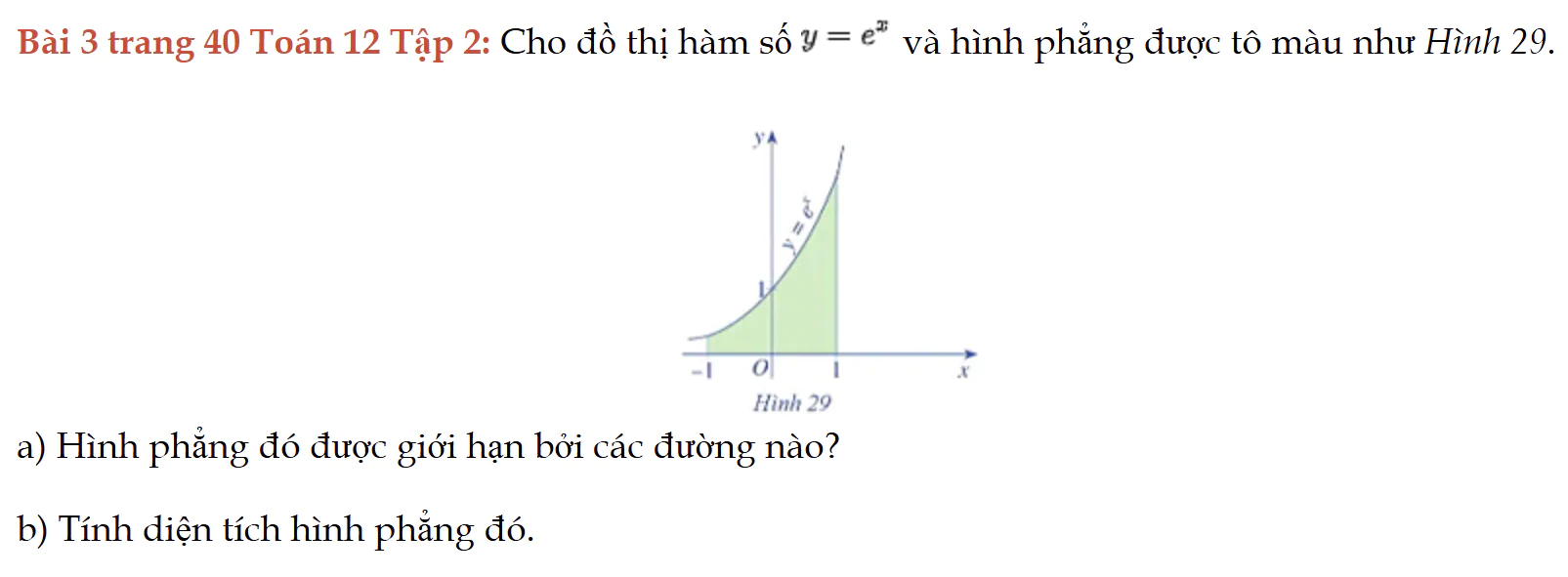
Bài 3 trang 40 Toán 12 Tập 2
Cho đồ thị hàm số, tính diện tích hình phẳng giới hạn bởi đồ thị. Bài 3 trang 40 Toán 12 Tập 2
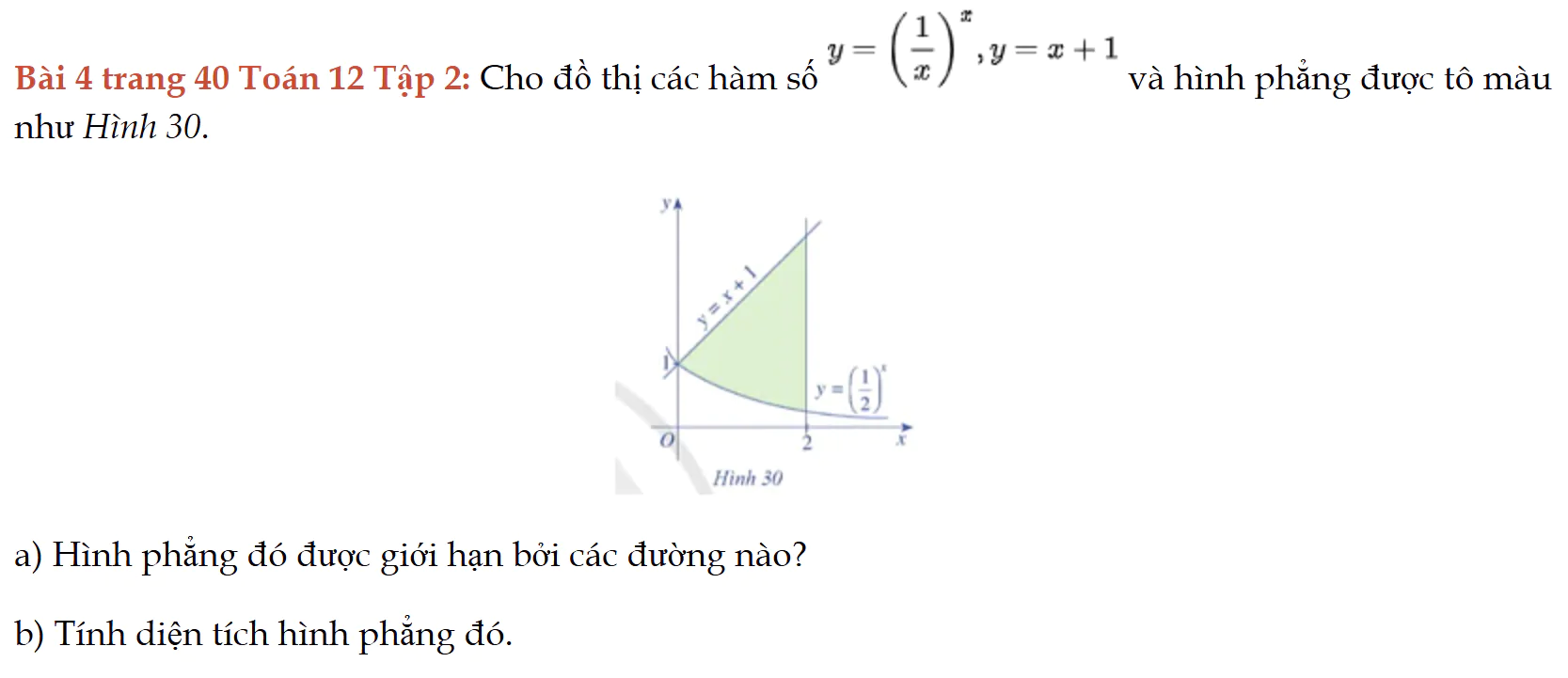
Bài 4 trang 40 Toán 12 Tập 2
Cho đồ thị các hàm số, tính diện tích hình phẳng được giới hạn bởi các đồ thị hàm số. Bài 4 trang 40 Toán 12 Tập 2
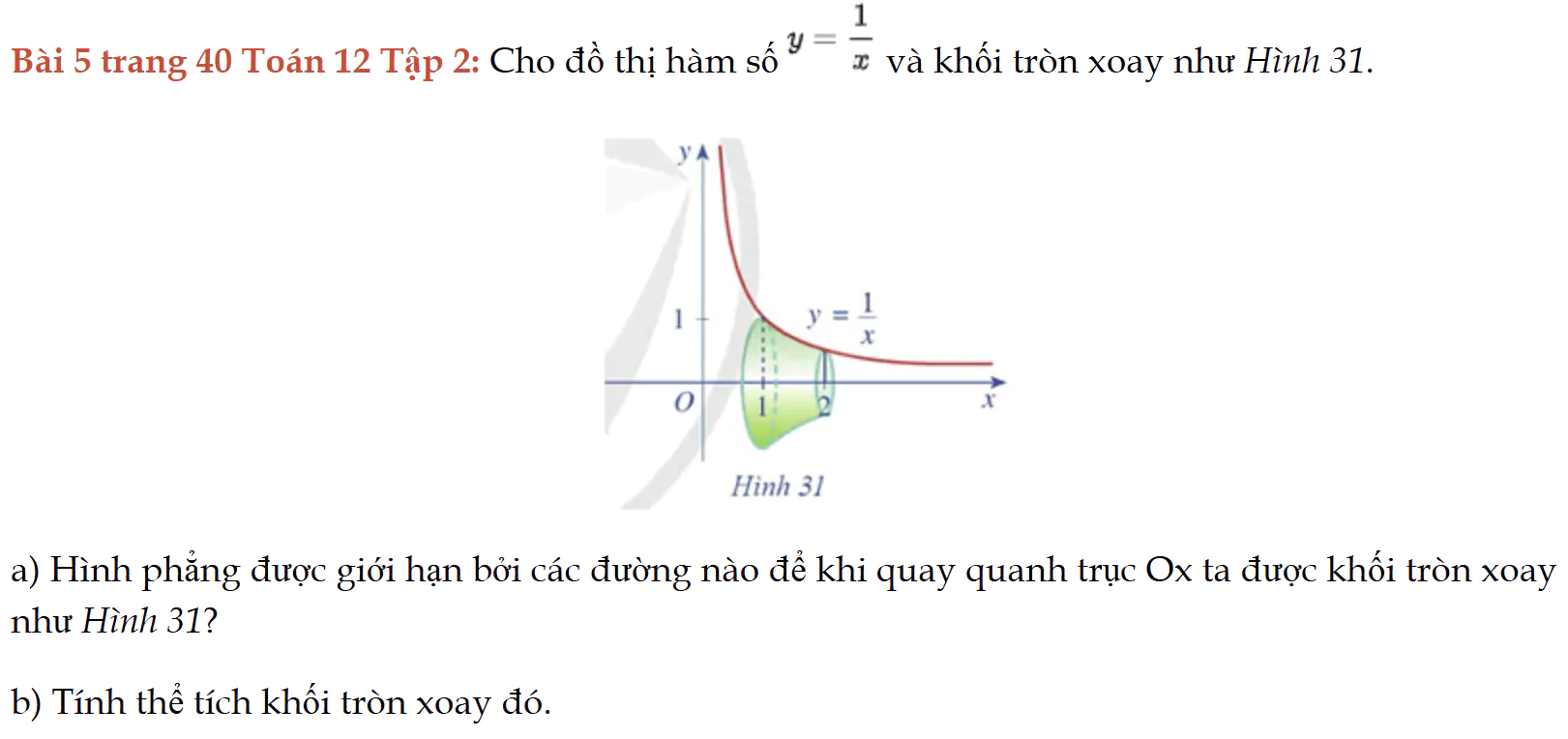
Bài 5 trang 40 Toán 12 Tập 2
Cho đồ thị hàm số, tính thể tích khối tròn xoay. Bài 5 trang 40 Toán 12 Tập 2
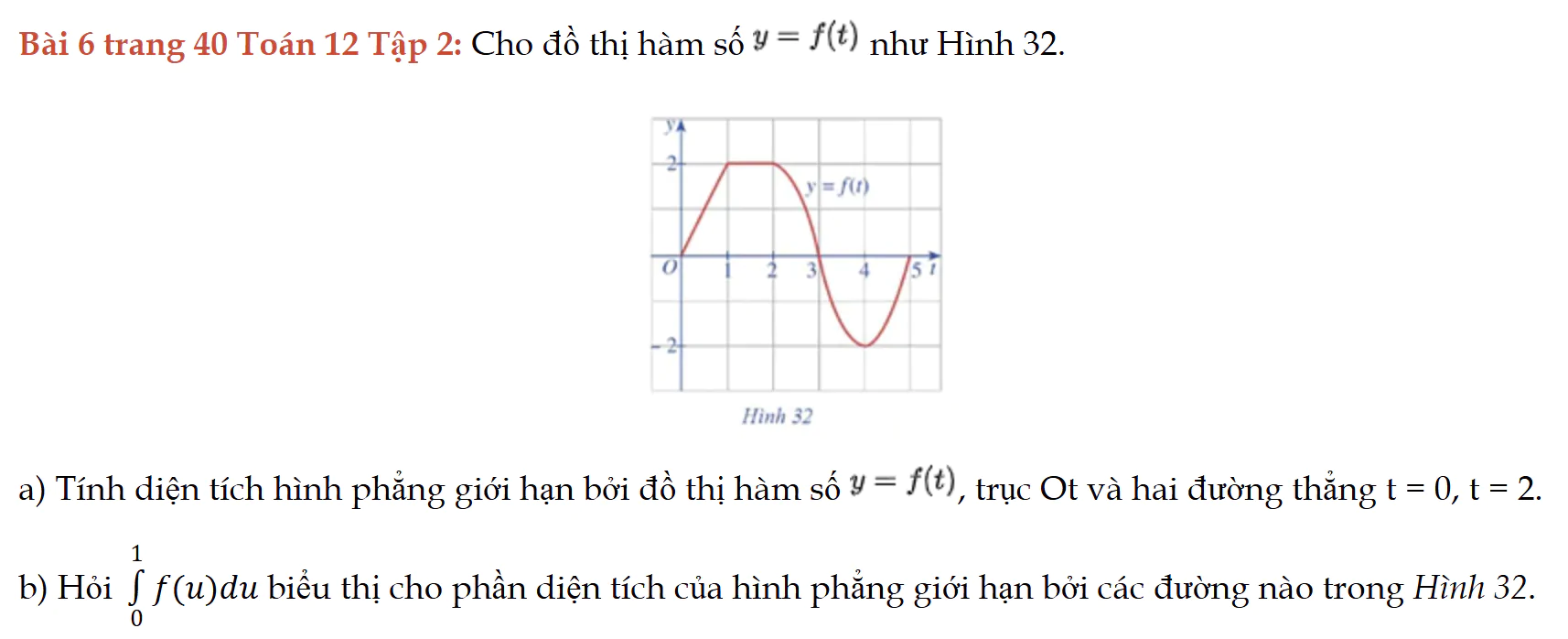
Bài 6 trang 40 Toán 12 Tập 2
Cho đồ thị hàm số, tính diện tích hình phẳng được giới hạn bới đồ thị. Bài 6 trang 40 Toán 12 Tập 2

Bài 7 trang 41 Toán 12 Tập 2
Cho chiều rộng, chiều cao parabol, tìm hàm parabol, tính diện tích parabol bằng tích phân. Bài 7 trang 41 Toán 12 Tập 2.

Bài 8 trang 41 Toán 12 Tập 2
Cho hàm số, tính diện tích phần được giới hạn. Bài 8 trang 41 Toán 12 Tập 2
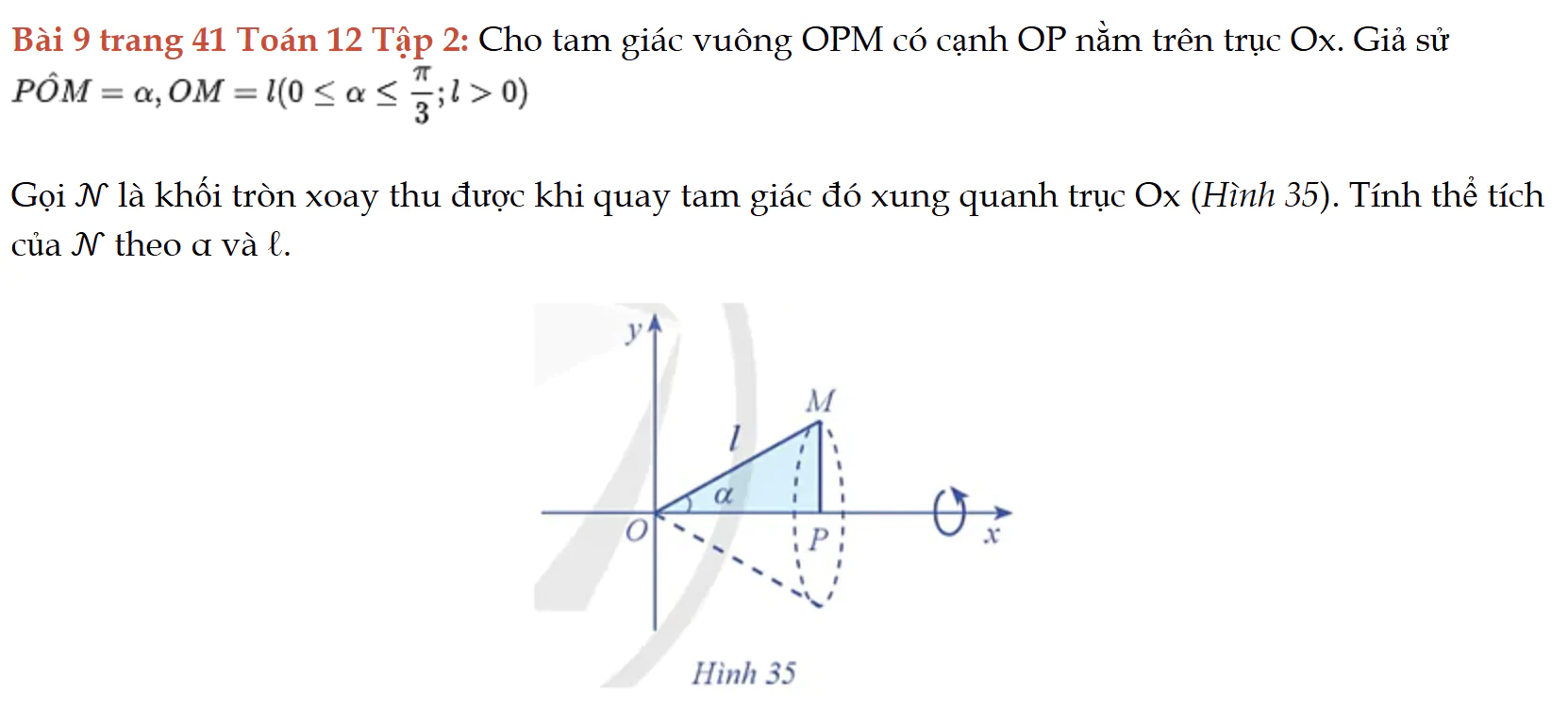
Bài 9 trang 41 Toán 12 Tập 2
Cho một hình tam giác quay quanh cạnh góc vuông, tính thể tích khối tròn xoay. Bài 9 trang 41 Toán 12 Tập 2

Bài 10 trang 41 Toán 12 Tập 2
Cho hàm số, tính thể tích khối tròn xoay. Bài 10 trang 41 Toán 12 Tập 2

Câu hỏi khởi động trang 28 Toán 12 Tập 2
ốm Bát Tràng là tên gọi chung của các loại đồ gốm Việt Nam được sản xuất tại làng Bát Tràng, thuộc xã Bát Tràng, huyện Gia Lâm, Hà Nội. Câu hỏi khởi động trang 28 Toán 12 Tập 2
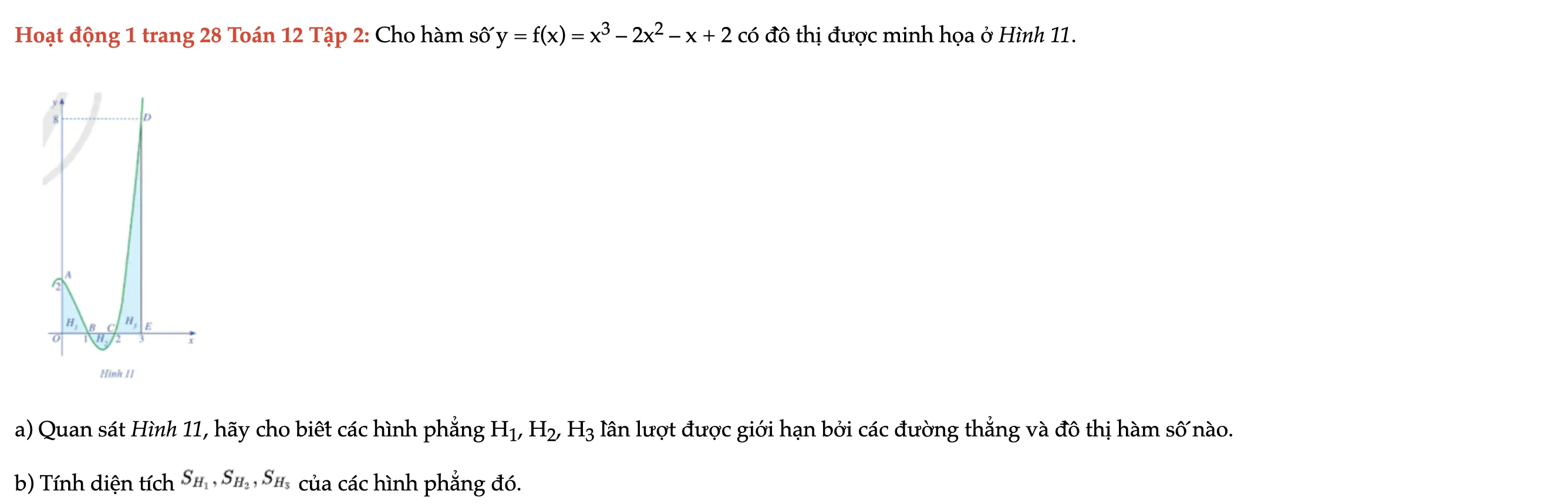
Hoạt động 1 trang 28 Toán 12 Tập 2
Cho hàm số y = f(x) có đồ thị được minh họa ở Hình 11. Quan sát Hình 11, hãy cho biết các hình phẳng H1, H2, H3 lần lượt được giới hạn bởi các đường thẳng và đồ thị hàm số nào. Hoạt động 1 trang 28 Toán 12 Tập 2

Luyện tập 1 trang 29 Toán 12 Tập 2
Trong Hình 13, tính diện tích hình phẳng giới hạn bởi đồ thị của hàm số y, trục Ox và hai đường thẳng x = – 1, x = 3. Luyện tập 1 trang 29 Toán 12 Tập 2
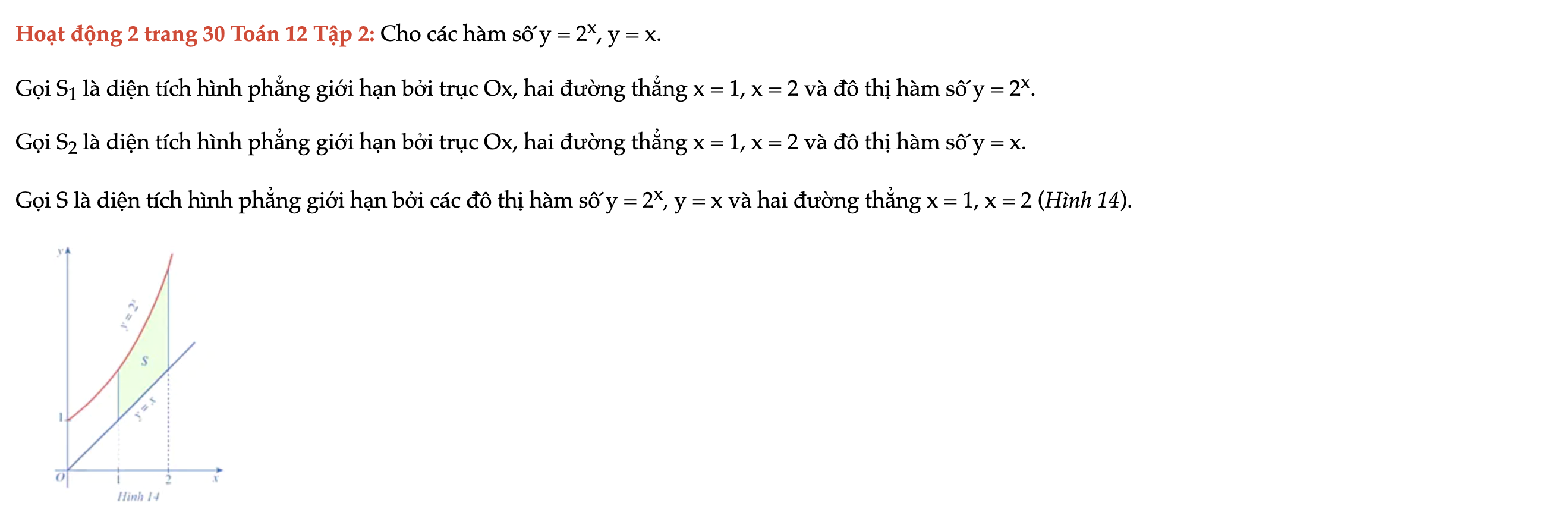
Hoạt động 2 trang 30 Toán 12 Tập 2
Cho các hàm số y = 2^x, y = x. Gọi S1 là diện tích hình phẳng giới hạn bởi trục Ox, hai đường thẳng x = 1, x = 2 và đồ thị hàm số y = 2^x. Hoạt động 2 trang 30 Toán 12 Tập 2

Luyện tập 2 trang 31 Toán 12 Tập 2
Tính diện tích hình phẳng giới hạn bởi các đồ thị hàm số sau. Luyện tập 2 trang 31 Toán 12 Tập 2

Hoạt động 3 trang 34 Toán 12 Tập 2
Cắt khối lập phương có cạnh bằng 1 bởi một mặt phẳng tùy ý vuông góc với trục Ox tại x, với 0 ≤ x ≤ 1 ta nhận được hình phẳng có diện tích là S(x) (Hình 17). Hoạt động 3 trang 34 Toán 12 Tập 2

Luyện tập 3 trang 35 Toán 12 Tập 2
Cắt một vật thể bởi hai mặt phẳng vuông góc với trục Ox tại x = 1 và x = 2. Một mặt phẳng tùy ý vuông góc với Ox tại x (1 ≤ x ≤ 2) cắt vật thể đó theo hình phẳng có diện tích là S(x) = 2x. Luyện tập 3 trang 35 Toán 12 Tập 2

Luyện tập 4 trang 36 Toán 12 Tập 2
Cho khối chóp cụt đều tạo bởi khối chóp đỉnh S, diện tích hai đáy lần lượt là B, B' và chiều cao h. Chọn trục Ox chứa đường cao của khối chóp và gốc O trùng với đỉnh S (Hình 21). Luyện tập 4 trang 36 Toán 12 Tập 2

Hoạt động 4 trang 37 Toán 12 Tập 2
Xét nửa hình tròn tâm O, bán kính r (Hình 24). Nửa hình tròn đó là hình phẳng giới hạn bởi trục Ox và đồ thị hàm số y = f(x). Tìm hàm số y = f(x). Hoạt động 4 trang 37 Toán 12 Tập 2
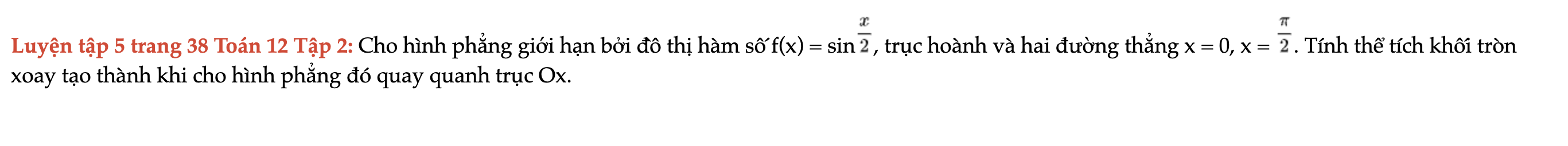
Luyện tập 5 trang 38 Toán 12 Tập 2
Cho hình phẳng giới hạn bởi đồ thị hàm số f(x) = sin(x/2), trục hoành và hai đường thẳng x = 0, x = π/2. Tính thể tích khối tròn xoay tạo thành khi cho hình phẳng đó quay quanh trục Ox. Luyện tập 5 trang 38 Toán 12 Tập 2
Giải bài tập Bài tập cuối chương 4

Bài 1 trang 42 Toán 12 Tập 2
Cho hàm số, t nguyên hàm. Bài 1 trang 42 Toán 12 Tập 2

Bài 2 trang 42 Toán 12 Tập 2
Cho nguyên hàm, tìm tích phân. Bài 2 trang 42 Toán 12 Tập 2

Bài 3 trang 42 Toán 12 Tập 2
Cho một tích phân, từ đó tính tích phân khác. Bài 3 trang 42 Toán 12 Tập 2
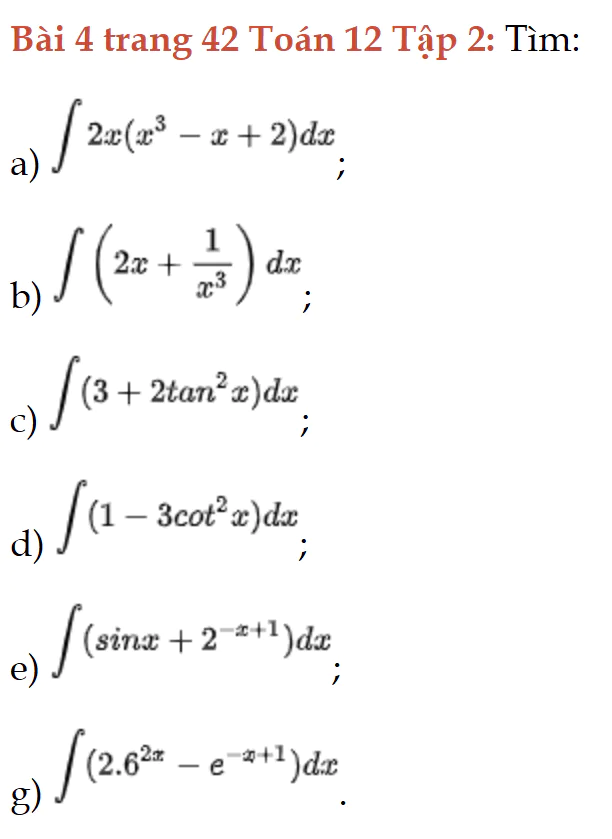
Bài 4 trang 42 Toán 12 Tập 2
Tính nguyên hàm. Bài 4 trang 42 Toán 12 Tập 2

Bài 5 trang 42 Toán 12 Tập 2
Cho hàm số, tìm nguyên hàm. Bài 5 trang 42 Ton 12 Tập 2
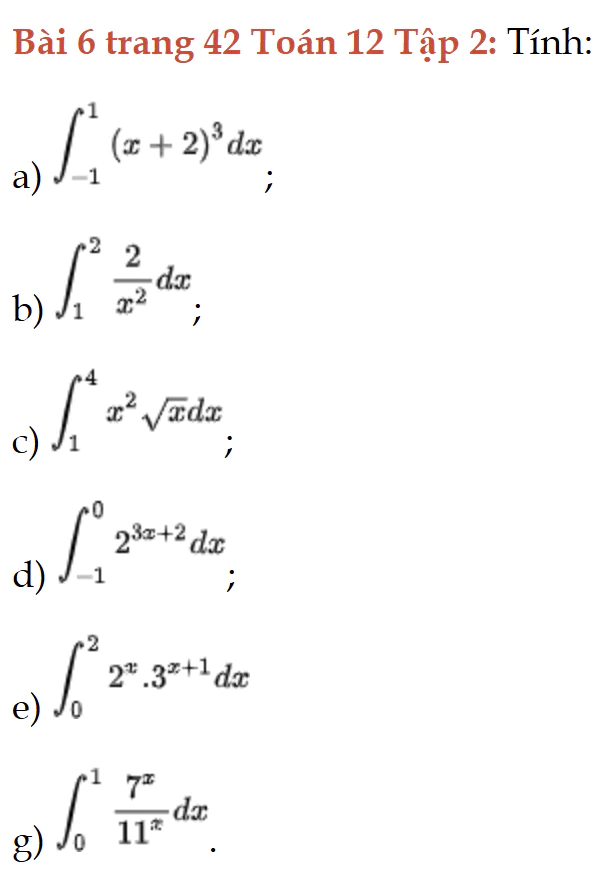
Bài 6 trang 42 Toán 12 Tập 2
Tính tích phân. Bài 6 trang 42 Toán 12 Tập 2

Bài 7 trang 42 Toán 12 Tập 2
Cho hàm số, tìm nguyên hàm. Bài 7 trang 42 Toán 12 Tập 2

Bài 8 trang 43 Toán 12 Tập 2
Cho hàm số, hàm số đạt giá trị lớn nhất khi nào. Bài 8 trang 43 Toán 12 Tập 2

Bài 9 trang 43 Toán 12 Tập 2
Cho hàm số, tìm nguyên hàm. Bài 9 trang 43 Toán 12 Tập 2

Bài 10 trang 43 Toán 12 Tập 2
Cho bảng số liệu, viết hàm số. Bài 10 trang 43 Toán 12 Tập 2
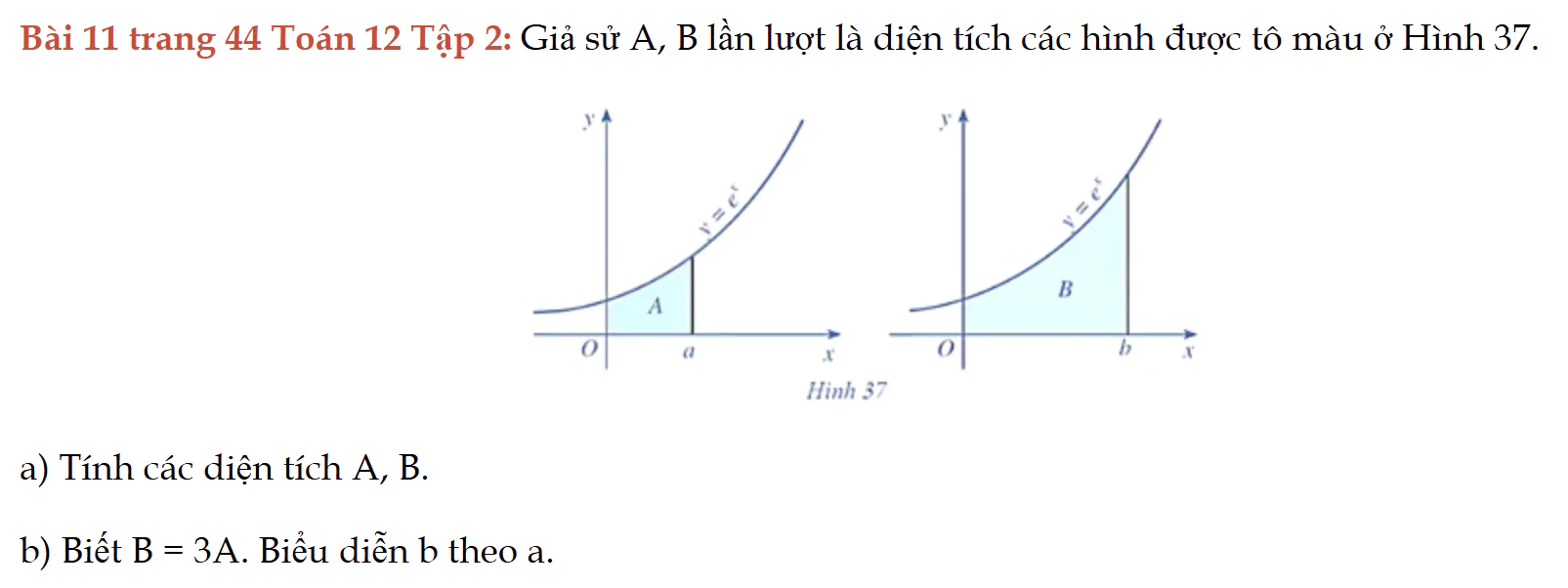
Bài 11 trang 44 Toán 12 Tập 2
Cho hàm số, tính diện tích giới hạn. Bài 11 trang 44 Toán 12 Tập 2

Bài 12 trang 44 Toán 12 Tập 2
Cho các điểm đi qua, viết hàm số, tính diện tích bằng tích phân. Bài 12 trang 44 Toán 12 Tập 2

Bài 13 trang 44 Toán 12 Tập 2
Cho hàm số, tính thể tích khối tròn xoay. Bài 13 trang 44 Toán 12 Tập 2