Giải bài tập Toán 12 Bài 3. Phương trình mặt cầu. | Cánh Diều
Hướng dẫn giải chi tiết Bài 3. Phương trình mặt cầu. Hai dạng phương trình mặt cầu. Cách xác định tâm và bán kính của mặt cầu. Vận dụng của phương trình mặt cầu.
Bài 1 trang 85 Toán 12 Tập 2
Bài 1 trang 85 Toán 12 Tập 2: Tâm của mặt cầu 
có tọa độ là:
A.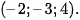 
B. 
.
C. 
.
D. 
Bài 2 trang 85 Toán 12 Tập 2
Bài 2 trang 85 Toán 12 Tập 2: Bán kính của mặt cầu 
bằng:
A. 
.
B.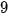 
.
C. 
D. 
.
Bài 3 trang 86 Toán 12 Tập 2
Bài 3 trang 86 Toán 12 Tập 2: Mặt cầu (S) tâm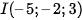 
bán kính 4 có phương trình là:
A.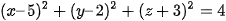 
.
B. 
C.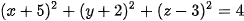 
.
D.
.
Bài 5 trang 86 Toán 12 Tập 2
Bài 5 trang 86 Toán 12 Tập 2: Cho phương trình 
Chứng minh rằng phương trình trên là phương trình của một mặt cầu. Xác định tâm và bán kính của mặt cầu đó.
Bài 4 trang 86 Toán 12 Tập 2
Bài 4 trang 86 Toán 12 Tập 2: Cho mặt cầu có phương trình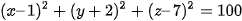 
.
b) Mỗi điểm 
nằm trong, nằm ngoài hay nằm trên mặt cầu đó?
Bài 6 trang 86 Toán 12 Tập 2
Bài 6 trang 86 Toán 12 Tập 2: Lập phương trình mặt cầu (S) trong mỗi trường hợp sau:
a) (S) có tâm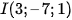 
và bán kính R = 2;
b) (S) có tâm 
và đi qua điểm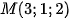 
;
c) (S) có đường kính là đoạn thẳng CD với 
và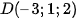 
.
Bài 7 trang 86 Toán 12 Tập 2
Bài 7 trang 86 Toán 12 Tập 2: Hệ thống định vị toàn cầu (tên tiếng Anh là: Global Positioning System, viết tắt là GPS) là một hệ thống cho phép xác định chính xác vị trí của một vật thể trong không gian (Hình 42). Ta có thể mô phỏng cơ chế hoạt động của hệ thống GPS trong không gian như sau: Trong cùng một thời điểm, toạ độ của một điểm M trong không gian sẽ được xác định bởi bốn vệ tinh cho trước, trên mỗi vệ tinh có một máy thu tín hiệu. Bằng cách so sánh sự sai lệch về thời gian từ lúc tín hiệu được phát đi với thời gian nhận phản hồi tín hiệu đó, mỗi máy thu tín hiệu xác định được khoảng cách từ vệ tinh đến vị trí M cần tìm tọa độ. Như vậy, điểm M là giao điểm của bốn mặt cầu với tâm lần lượt là bốn vệ tinh đã cho.
Ta xét một ví dụ cụ thể như sau: Trong không gian với hệ tọa độ Oxyz, cho bốn vệ tinh 
. Tìm tọa độ của điểm M trong không gian biết khoảng cách từ các vệ tinh đến điểm M lần lượt là 
.
Câu hỏi khởi động trang 81 Toán 12 Tập 2
Hình 38 mô tả một mặt cầu trong không gian.
Trong không gian với hệ tọa độ Oxyz, phương trình của mặt cầu được lập như thế nào?
Hoạt động 1 trang 81 Toán 12 Tập 2
Nếu quay đường tròn tâm I bán kính R quanh đường kính AB một vòng (Hình 39) thì hình tạo thành được gọi là mặt cầu. Những điểm thuộc mặt cầu đó cách I một khoảng bằng bao nhiêu?
Luyện tập 1 trang 82 Toán 12 Tập 2
Trong không gian với hệ tọa độ Oxyz, cho điểm I(1; 2; 3) và mặt cầu tâm I đi qua điểm A(0; 4; 5). Tính đường kính của mặt cầu đó.
Hoạt động 2 trang 82 Toán 12 Tập 2
Cho hai điểm M(x; y; z) và I(a; b; c).
a) Viết công thức tính khoảng cách giữa hai điểm M và I.
b) Nêu mối liên hệ giữa x, y, và z để điểm M nằm trên mặt cầu tâm I bán kính R.
Luyện tập 2 trang 82 Toán 12 Tập 2
Tìm tâm và bán kính của mặt cầu có phương trình: x2 + (y + 5)2 + (z + 1)2 = 2.
Luyện tập 3 trang 82 Toán 12 Tập 2
Viết phương trình của mặt cầu, biết:
a) Tâm O bán kính R với O là gốc tọa độ;
b) Đường kính AB với A(1; 2; 1), B(3; 4; 7).
Luyện tập 4 trang 83 Toán 12 Tập 2
Chứng minh rằng phương trình x2 + y2 + z2 – 6x – 2y – 4z – 11 = 0 là phương trình của một mặt cầu. Tìm tâm I và bán kính R của mặt cầu đó.
Luyện tập 5 trang 85 Toán 12 Tập 2
Trong Ví dụ 6, giả sử người đi biển di chuyển theo đường thẳng từ vị trí I(21; 35; 50) đến vị trí D(5121; 658; 0). Tìm vị trí cuối cùng trên đoạn thẳng ID sao cho người đi biển còn có thể nhìn thấy được ánh sáng từ ngọn hải đăng.