Giải bài tập Toán 12 Bài 2. Phương trình đường thẳng. | Cánh Diều
Hướng dẫn giải chi tiết Bài 2. Phương trình đường thẳng. Vecto chỉ phương, phương trình tham số, phương trình chính tắc của đường thẳng. Điều kiện để hai đường thẳng song song, trùng nhau, cắt nhau, chéo nhau, vuông góc. Góc.
Bài 1 trang 78 Toán 12 Tập 2
Bài 1 trang 78 Toán 12 Tập 2: Đường thẳng đi qua điểm  nhận làm vectơ chỉ phương có phương trình tham số là:
nhận làm vectơ chỉ phương có phương trình tham số là:
A. 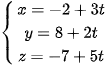
B. 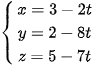
C. 
D. 
Bài 2 trang 78 Toán 12 Tập 2
Bài 2 trang 78 Toán 12 Tập 2: Đường thẳng đi qua điểm 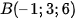 nhận
nhận  làm vectơ chỉ phương có phương trình chính tắc là:
làm vectơ chỉ phương có phương trình chính tắc là:
A. 
B. 
C. 
D. 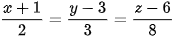
Bài 3 trang 78 Toán 12 Tập 2
Bài 3 trang 78 Toán 12 Tập 2: Mặt phẳng  vuông góc với mặt phẳng nào sau đây?
vuông góc với mặt phẳng nào sau đây?
A.  .
.
B.  .
.
C. 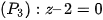 .
.
D.  .
.
Bài 4 trang 78 Toán 12 Tập 2
Bài 4 trang 78 Toán 12 Tập 2: Cho đường thẳng ∆ có phương trình tham số 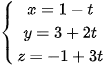 (t là tham số).
(t là tham số).
a) Chỉ ra tọa độ hai điểm thuộc đường thẳng ∆.
b) Điểm nào trong hai điểm 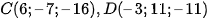 thuộc đường thẳng ∆?
thuộc đường thẳng ∆?
Bài 5 trang 78 Toán 12 Tập 2
Bài 5 trang 78 Toán 12 Tập 2: Viết phương trình tham số và phương trình chính tắc của đường thẳng ∆ trong mỗi trường hợp sau:
a) ∆ đi qua điểm  và có vectơ chỉ phương
và có vectơ chỉ phương 
b) ∆ đi qua điểm 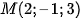 và
và  .
.
Bài 6 trang 79 Toán 12 Tập 2
Bài 6 trang 79 Toán 12 Tập 2: Xác định vị trí tương đối của hai đường thẳng ∆1, ∆2 trong mỗi trường hợp sau:
a)  và
và  (t là tham số)
(t là tham số)
b) 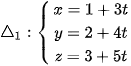 (t là tham số) và
(t là tham số) và 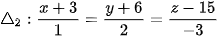
c)  và
và  .
.
Bài 7 trang 79 Toán 12 Tập 2
Bài 7 trang 79 Toán 12 Tập 2: Tính góc giữa hai đường thẳng ∆1, ∆2 trong mỗi trường hợp sau (làm tròn kết quả đến hàng đơn vị của độ):
a)  và
và  (
( là tham số )
là tham số )
b)  (t là tham số) và
(t là tham số) và 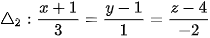
c)  và
và 
Bài 8 trang 79 Toán 12 Tập 2
Bài 8 trang 79 Toán 12 Tập 2: Tính góc giữa đường thẳng ∆ và mặt phẳng (P) trong mỗi trường hợp sau (làm tròn kết quả đến hàng đơn vị của độ):
a)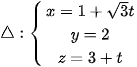 (t là tham số) và
(t là tham số) và  ;
;
b) 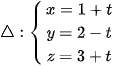 (t là tham số) và
(t là tham số) và 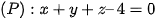
Bài 9 trang 79 Toán 12 Tập 2
Bài 9 trang 79 Toán 12 Tập 2: Tính góc giữa hai mặt phẳng  và
và 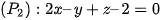 .
.
Bài 10 trang 80 Toán 12 Tập 2
Bài 10 trang 80 Toán 12 Tập 2: Trong không gian với hệ trục tọa độ Oxyz, cho hình chóp S.ABCD có các đỉnh lần lượt là  với a > 0 (Hình 36).
với a > 0 (Hình 36).
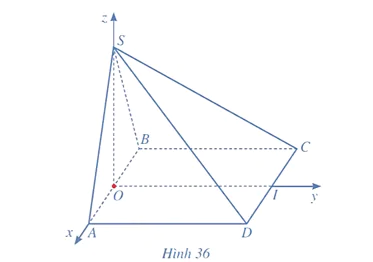
a) Xác định tọa độ của các vectơ  . Từ đó tính góc giữa hai đường thẳng SA và CD (làm tròn kết quả đến hàng đơn vị của độ).
. Từ đó tính góc giữa hai đường thẳng SA và CD (làm tròn kết quả đến hàng đơn vị của độ).
b) Chỉ ra một vectơ pháp tuyến của mặt phẳng (SAC). Từ đó tính góc giữa đường thẳng SD và mặt phẳng (SAC) (làm tròn kết quả đến hàng đơn vị của độ).
Bài 11 trang 80 Toán 12 Tập 2
Bài 11 trang 80 Toán 12 Tập 2: Trong không gian với hệ tọa độ Oxyz (đơn vị trên mỗi trục tọa độ là kilômét), một máy bay đang ở vị trí  và sẽ hạ cánh ở vị trí
và sẽ hạ cánh ở vị trí  trên đường băng EG (Hình 37).
trên đường băng EG (Hình 37).

a) Viết phương trình đường thẳng AB.
b) Hãy cho biết góc trượt (góc giữa đường bay AB và mặt phẳng nằm ngang (Oxy)) có nằm trong phạm vi cho phép từ 2,5° đến 3,5° hay không.
c) Có một lớp mây được mô phỏng bởi một mặt phẳng (α) đi qua ba điểm  . Tìm tọa độ của điểm C là vị trí mà máy bay xuyên qua đám mây để hạ cánh.
. Tìm tọa độ của điểm C là vị trí mà máy bay xuyên qua đám mây để hạ cánh.
d) Tìm tọa độ của điểm D trên đoạn thẳng AB là vị trí mà máy bay ở độ cao 120 m.
e) Theo quy định an toàn bay, người phi công phải nhìn thấy điểm đầu  của đường băng ở độ cao tối thiểu là 120 m. Hỏi sau khi ra khỏi đám mây, người phi công có đạt được quy định an toàn đó hay không? Biết rằng tầm nhìn của người phi công sau khi ra khỏi đám mây là 900 m (Nguồn: R.Larson and B.Edwards, Calculus 10e, Cengage, 2014).
của đường băng ở độ cao tối thiểu là 120 m. Hỏi sau khi ra khỏi đám mây, người phi công có đạt được quy định an toàn đó hay không? Biết rằng tầm nhìn của người phi công sau khi ra khỏi đám mây là 900 m (Nguồn: R.Larson and B.Edwards, Calculus 10e, Cengage, 2014).
Câu hỏi khởi động trang 65 Toán 12 Tập 2
Cầu Bãi Cháy nối Hòn Gai và Bãi Cháy (Quảng Ninh). Dây cáp của cầu gợi nên hình ảnh đường thẳng trong không gian với hệ tọa độ Oxyz (Hình 22).
Trong hệ tọa độ Oxyz, phương trình của đường thẳng là gì? Làm thế nào để lập được phương trình của đường thẳng?
Hoạt động 1 trang 65 Toán 12 Tập 2
Cho hình hộp ABCD.A'B'C'D' (Hình 23). Giá của vectơ  và đường thẳng AC có vị trí tương đối như thế nào?
và đường thẳng AC có vị trí tương đối như thế nào?
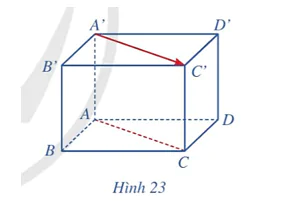
Luyện tập 1 trang 65 Toán 12 Tập 2
Trong Hình 23, vectơ 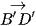 có là vectơ chỉ phương của đường thẳng BD hay không? Vì sao?
có là vectơ chỉ phương của đường thẳng BD hay không? Vì sao?

Hoạt động 2 trang 66 Toán 12 Tập 2
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng ∆ đi qua điểm M0(1; 2; 3) và có vectơ chỉ phương  = (2; 3; 5). Xét điểm M(x; y; z) nằm trên ∆ (Hình 24).
= (2; 3; 5). Xét điểm M(x; y; z) nằm trên ∆ (Hình 24).

a) Nêu nhận xét về phương của hai vectơ 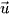 và
và  .
.
b) Có hay không số thực t sao cho  ?
?
c) Hãy biểu diễn x, y, z qua t.
d) Tọa độ (x; y; z) của điểm M (nằm trên ∆) có thỏa mãn hệ phương trình:
 hay không?
hay không?
Luyện tập 2 trang 67 Toán 12 Tập 2
Viết phương trình tham số của đường thẳng ∆, biết ∆ đi qua điểm C(1; 2; – 4) và vuông góc với mặt phẳng (P): 3x – y + 2z – 1 = 0.
Hoạt động 3 trang 67 Toán 12 Tập 2
Cho đường thẳng ∆ có phương trình tham số:  (t là tham số).
(t là tham số).
Tọa độ (x; y; z) của điểm M (nằm trên ∆) có thỏa mãn hệ phương trình  hay không?
hay không?
Luyện tập 3 trang 68 Toán 12 Tập 2
Viết phương trình chính tắc của đường thẳng ∆, biết phương trình tham số của ∆ là:  (t là tham số).
(t là tham số).
Hoạt động 4 trang 68 Toán 12 Tập 2
Trong không gian với hệ tọa độ Oxyz, cho điểm A(1; 2; 3) và B(3; 5; 9).
a) Hãy chỉ ra một vectơ chỉ phương của đường thẳng AB.
b) Viết phương trình tham số của đường thẳng AB.
c) Viết phương trình chính tắc của đường thẳng AB.
Luyện tập 4 trang 69 Toán 12 Tập 2
Viết phương trình chính tắc của đường thẳng OM, biết M(a; b; c) với abc ≠ 0.
Hoạt động 5 trang 69 Toán 12 Tập 2
Cho hai đường thẳng phân biệt ∆1, ∆2 lần lượt đi qua các điểm M1, M2 và tương ứng có vectơ chỉ phương là  .
.
a) Giả sử ∆1 song song với ∆2 (Hình 25). Các cặp vectơ sau có cùng phương hay không: 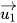 và
và  ;
;  và
và 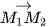 ?
?

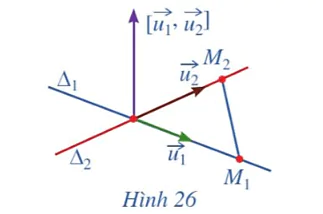
b) Giả sử ∆1 và ∆2 cắt nhau (Hình 26). Hai vectơ 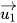 và
và  có cùng phương hay không? Ba vectơ
có cùng phương hay không? Ba vectơ  và
và 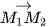 có đồng phẳng hay không?
có đồng phẳng hay không?
c) Giả sử ∆1 và ∆2 chéo nhau (Hình 27). Hai vectơ 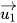 và
và  có cùng phương hay không? Ba vectơ
có cùng phương hay không? Ba vectơ  và
và 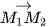 có đồng phẳng hay không?
có đồng phẳng hay không?

Luyện tập 5 trang 70 Toán 12 Tập 2
Bằng cách giải hệ phương trình, xác định vị trí tương đối của hai đường thẳng  và
và  (t1, t2 là tham số).
(t1, t2 là tham số).
Hoạt động 6 trang 71 Toán 12 Tập 2
Cho hai đường thẳng ∆1, ∆2 trong không gian có vectơ chỉ phương lần lượt là  . Giả sử ∆'1, ∆'2 là hai đường thẳng cùng đi qua điểm I và lần lượt song song (hoặc trùng) với ∆1, ∆2 (Hình 28).
. Giả sử ∆'1, ∆'2 là hai đường thẳng cùng đi qua điểm I và lần lượt song song (hoặc trùng) với ∆1, ∆2 (Hình 28).
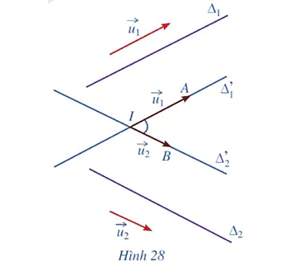
a) Nếu mối liên hệ giữa hai góc (∆1, ∆2) và (∆'1, ∆'2).
b) Gọi A và B là các điểm lần lượt thuộc hai đường thẳng ∆'1 và ∆'2 sao cho  . So sánh: cos(∆'1, ∆'2),
. So sánh: cos(∆'1, ∆'2), 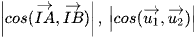 .
.
c) So sánh cos (∆1, ∆2) và 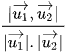 .
.
Luyện tập 6 trang 72 Toán 12 Tập 2
Cho đường thẳng  . Tính côsin của góc giữa đường thẳng ∆ và các trục tọa độ.
. Tính côsin của góc giữa đường thẳng ∆ và các trục tọa độ.
Hoạt động 7 trang 73 Toán 12 Tập 2
Cho mặt phẳng (P) có vectơ pháp tuyến là 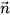 , đường thẳng ∆ có vectơ chỉ phương là
, đường thẳng ∆ có vectơ chỉ phương là  và đường thẳng ∆ cắt mặt phẳng (P) tại I. Gọi ∆' là hình chiếu của ∆ trên mặt phẳng (P) (Hình 29).
và đường thẳng ∆ cắt mặt phẳng (P) tại I. Gọi ∆' là hình chiếu của ∆ trên mặt phẳng (P) (Hình 29).

a) Hãy xác định góc giữa đường thẳng ∆ và mặt phẳng (P).
Ta kí hiệu góc đó là (∆, (P)).
b) So sánh sin (∆, (P)) và 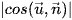 .
.
Luyện tập 7 trang 73 Toán 12 Tập 2
Cho mặt phẳng (P) có vectơ pháp tuyến  = (A; B; C). Tính sin của góc giữa mặt phẳng (P) và các trục tọa độ.
= (A; B; C). Tính sin của góc giữa mặt phẳng (P) và các trục tọa độ.
Hoạt động 8 trang 74 Toán 12 Tập 2
Cho hai mặt phẳng (P1) và (P2). Lấy hai đường thẳng ∆1, ∆2 sao cho ∆1 ⊥ (P1), ∆2 ⊥ (P2) (Hình 31).

a) Nêu cách xác định góc giữa hai đường thẳng ∆1, ∆2.
b) Góc đó có phụ thuộc vào việc chọn hai đường thẳng ∆1, ∆2 như trên hay không?
Luyện tập 8 trang 74 Toán 12 Tập 2
Trong Ví dụ 10, tính góc giữa hai mặt phẳng (BCC'B') và (CDA'B').
Hoạt động 9 trang 75 Toán 12 Tập 2
Cho hai mặt phẳng (P1) và (P2). Gọi 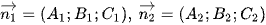 lần lượt là hai vectơ pháp tuyến của (P1), (P2); ∆1, ∆2 lần lượt là giá của hai vectơ
lần lượt là hai vectơ pháp tuyến của (P1), (P2); ∆1, ∆2 lần lượt là giá của hai vectơ  (Hình 33). So sánh:
(Hình 33). So sánh:
a) cos ((P1), (P2)) và cos (∆1, ∆2);
b) cos (∆1, ∆2) và  .
.

Luyện tập 9 trang 75 Toán 12 Tập 2
Cho mặt phẳng (P) có vectơ pháp tuyến  = (A; B; C). Tính côsin của góc giữa mặt phẳng (P) và các mặt phẳng tọa độ.
= (A; B; C). Tính côsin của góc giữa mặt phẳng (P) và các mặt phẳng tọa độ.