Giải bài tập Bài 5 trang 8 Toán 12 Tập 2 | SGK Toán 12 - Cánh diều
Hướng dẫn giải chi tiết từng bước bài tập Bài 5 trang 8 Toán 12 Tập 2. Bài 1. Nguyên hàm.. SGK Toán 12 - Cánh diều
Đề bài:
Bài 5 trang 8 Toán 12 Tập 2: Tại một lễ hội dân gian, tốc độ thay đổi lượng khách tham dự được biểu diễn bằng hàm số B'(t) = 20t3 – 300t2 + 1000t, trong đó t tính bằng giờ (0 ≤ t ≤ 15), B'(t) tính bằng khách/giờ.
(Nguồn: A. Bigalke et al., Mathematik, Grundkurs ma-1, Cornelsen 2016)
Biết rằng sau một giờ, 500 người đã có mặt tại lễ hội.
a) Viết công thức của hàm số B(t) biểu diễn số lượng khách tham dự lễ hội với 0 ≤ t ≤ 15.
b) Sau 3 giờ sẽ có bao nhiêu khách tham dự lễ hội?
c) Số lượng khách tham dự lễ hội lớn nhất là bao nhiêu?
d) Tại thời điểm nào thì tốc độ thay đổi lượng khách tham dự lễ hội là lớn nhất?
Đáp án và cách giải chi tiết:
a) Hàm số B(t) là một nguyên hàm của hàm số B'(t).
Ta có 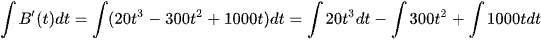
Suy ra B(t) = 5t4 – 100t3 + 500t2 + C.
Vì sau một giờ, 500 người đã có mặt tại lễ hội nên B(1) = 500.
Do đó, 5.14 – 100.13 + 500.12 + C = 500, suy ra C = 95.
Vậy công thức của hàm số B(t) biểu diễn số lượng khách tham dự lễ hội là
B(t) = 5t4 – 100t3 + 500t2 + 95 (0 ≤ t ≤ 15).
b) Ta có B(3) = 5.34 – 100.33 + 500.32 + 95 = 2300.
Vậy sau 3 giờ có 2300 khách tham dự lễ hội.
c) Số lượng khách tham dự lễ hội lớn nhất chính là giá trị lớn nhất của hàm số B(t) trên đoạn [0; 15].
Ta có B'(t) = 20t3 – 300t2 + 1000t.
Trên khoảng (0; 15), B'(t) = 0 khi t = 5 hoặc t = 10.
B(0) = 95; B(5) = 3220; B(10) = 95; B(15) = 28 220.
Do đó, 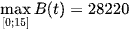 tại t = 15.
tại t = 15.
Vậy số lượng khách tham dự lễ hội lớn nhất là 28 220 khách sau 15 giờ.
d) Tốc độ thay đổi lượng khách tham dự lễ hội lớn nhất chính là giá trị lớn nhất của hàm số B'(t) trên đoạn [0; 15].
Ta có B''(t) = (20t3 – 300t2 + 1000t)' = 60t2 – 600t + 1000.
Trên khoảng (0; 15), B''(t) = 0 khi 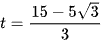 hoặc
hoặc 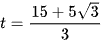 .
.
B'(0) = 0; 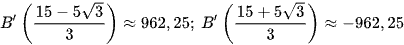 ; B'(15) = 15 000.
; B'(15) = 15 000.
Do đó, 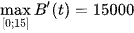 tại t = 15.
tại t = 15.
Nguồn: loigiaitoan.com
Tổng số đánh giá:
Xếp hạng: / 5 sao
Bài tập liên quan:
Câu hỏi khởi động trang 3 Toán 12 Tập 2
Một hòn đá rơi từ mỏm đá có độ cao 150 m so với mặt đất theo phương thẳng đứng. Biết tốc độ rơi của hòn đá (tính theo đơn vị m/s) tại thời điểm t (tính theo giây) được cho bởi công thức v(t) = 9,8t.
Quãng đường rơi được S của hòn đá tại thời điểm t được cho bởi công thức nào? Sau bao nhiêu giây thì hòn đá chạm đến mặt đất?
Hoạt động 1 trang 3 Toán 12 Tập 2
Cho hàm số F(x) = x3, x ∈ (– ∞; + ∞). Tính F'(x).
Hoạt động 2 trang 4 Toán 12 Tập 2
Cho hàm số F(x) = x3 – 1, x ∈ ℝ và G(x) = x3 + 5, x ∈ ℝ.
a) Cả hai hàm số F(x) và G(x) có phải là nguyên hàm của hàm số f(x) = 3x2 trên ℝ hay không?
b) Hiệu F(x) – G(x) có phải là một hằng số C (không phụ thuộc vào x) hay không?
Luyện tập 2 trang 4 Toán 12 Tập 2
Tìm tất cả các nguyên hàm của hàm số f(x) = cos x trên ℝ.
Hoạt động 3 trang 5 Toán 12 Tập 2
Cho f(x) là hàm số liên tục trên K, k là hằng số thực khác 0.
a) Giả sử F(x) là một nguyên hàm của hàm số f(x) trên K. Hỏi kF(x) có phải là nguyên hàm của hàm số kf(x) trên K hay không?
b) Giả sử G(x) là một nguyên hàm của hàm số kf(x) trên K. Đặt G(x) = kH(x) trên K. Hỏi H(x) có phải là nguyên hàm của hàm số f(x) trên K hay không?
c) Nêu nhận xét về  và
và  .
.
Hoạt động 4 trang 6 Toán 12 Tập 2
Cho f(x), g(x) là hai hàm số liên tục trên K.
a) Giả sử F(x), G(x) lần lượt là nguyên hàm của các hàm số f(x), g(x) trên K. Hỏi F(x) + G(x) có phải là nguyên hàm của hàm số f(x) + g(x) trên K hay không?
b) Giả sử H(x), F(x) lần lượt là nguyên hàm của các hàm số f(x) + g(x), f(x) trên K. Đặt G(x) = H(x) – F(x) trên K. Hỏi G(x) có phải là nguyên hàm của hàm số g(x) trên K hay không?
c) Nêu nhận xét về  và
và 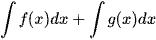 .
.
Bài 1 trang 7 Toán 12 Tập 2
Bài 1 trang 7 Toán 12 Tập 2: Hàm số là nguyên hàm của hàm số:
A. f(x) = 3x2.
B. 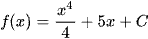 .
.
C. 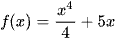 .
.
D. f(x) = 3x2 + 5x.
Bài 2 trang 7 Toán 12 Tập 2
Bài 2 trang 7 Toán 12 Tập 2: Tìm nguyên hàm của các hàm số sau:
a) f(x) = 3x2 + x;
b) f(x) = 9x2 – 2x + 7;
c) f(x) = (4x – 3)(x2 + 3).
Bài 3 trang 7 Toán 12 Tập 2
Bài 3 trang 7 Toán 12 Tập 2: Tìm nguyên hàm F(x) của hàm số f(x) = 6x5 + 2x – 3, biết F(–1) = –5.
Bài 4 trang 8 Toán 12 Tập 2
Bài 4 trang 8 Toán 12 Tập 2: Một vườn ươm cây cảnh bán một cây sau 6 năm trồng và uốn tạo dáng. Tốc độ tăng trưởng trong suốt 6 năm được tính xấp xỉ bởi công thức h'(t) = 1,5t + 5, trong đó h(t) (cm) là chiều cao của cây sau t (năm) (Nguồn: R. Larson and B. Edwards, Calculus 10e Cengage 2014). Biết rằng, cây con khi được trồng cao 12 cm.
a) Viết công thức tính chiều cao của cây sau t năm.
b) Khi được bán, cây cao bao nhiêu centimét?
Bài 6 trang 8 Toán 12 Tập 2
Bài 6 trang 8 Toán 12 Tập 2: Đối với các dự án xây dựng, chi phí nhân công lao động được tính theo số ngày công. Gọi m(t) là số lượng công nhân được sử dụng ở ngày thứ t (kể từ khi khởi công dự án). Gọi M(t) là số ngày công được tính đến hết ngày thứ t (kể từ khi khởi công dự án). Trong kinh tế xây dựng, người ta đã biết rằng M'(t) = m(t).
Một công trình xây dựng dự kiến hoàn thành trong 400 ngày. Số lượng công nhân được sử dụng cho bởi hàm số m(t) = 800 – 2t,
trong đó t tính theo ngày (0 ≤ t ≤ 400), m(t) tính theo người.
(Nguồn: A. Bigalke et al., Mathematik, Grundkurs ma-1, Cornelsen 2016)
Đơn giá cho một ngày công lao động là 400 000 đồng.
Tính chi phí nhân công lao động của công trình đó (cho đến lúc hoàn thành).
Luyện tập 1 trang 4 Toán 12 Tập 2
Hàm số F(x) = cot x là nguyên hàm của hàm số nào? Vì sao?
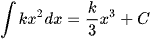 (k ≠ 0).
(k ≠ 0). với n là số nguyên dương.
với n là số nguyên dương. .
.