Giải bài tập Bài 7 trang 27 Toán 12 Tập 2 | SGK Toán 12 - Cánh diều
Hướng dẫn giải chi tiết từng bước bài tập Bài 7 trang 27 Toán 12 Tập 2. Bài 3. Tích phân.. SGK Toán 12 - Cánh diều
Đề bài:
Bài 7 trang 27 Toán 12 Tập 2: a) Cho một vật chuyển động với vận tốc y = v(t) (m/s). Cho 0 < a < b và v(t) > 0 với mọi t ∈ [a; b]. Hãy giải thích vì sao 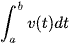 biểu thị quãng đường mà vật đi được trong khoảng thời gian từ a đến b (a, b tính theo giây).
biểu thị quãng đường mà vật đi được trong khoảng thời gian từ a đến b (a, b tính theo giây).
b) Áp dụng công thức ở câu a) để giải bài toán sau: Một vật chuyển động với vận tốc v(t) = 2 – sin t (m/s). Tính quãng đường vật di chuyển trong khoảng thời gian từ thời điểm t = 0 (giây) đến thời điểm 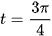 (giây).
(giây).
Đáp án và cách giải chi tiết:
a) Gọi s(t) là quãng đường đi được của chuyển động.
Ta có vận tốc là đạo của quãng đường: s'(t) = v(t). Do đó hàm số s(t) là một nguyên hàm của hàm số v(t). Khi đó ta có 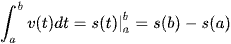
Vậy 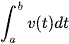 biểu thị quãng đường mà vật đi được trong khoảng thời gian từ a đến b.
biểu thị quãng đường mà vật đi được trong khoảng thời gian từ a đến b.
b) Quãng đường vật đó di chuyển trong khoảng thời gian từ thời điểm t = 0 (giây) đến thời điểm 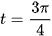 (giây) là:
(giây) là:
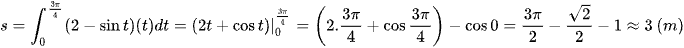
Nguồn: loigiaitoan.com
Tổng số đánh giá:
Xếp hạng: / 5 sao
Bài tập liên quan:
Bài 8 trang 27 Toán 12 Tập 2
Bài 8 trang 27 Toán 12 Tập 2: Một vật chuyển động với vận tốc được cho bởi đồ thị ở Hình 9.

a) Tính quãng đường mà vật di chuyển được trong 1 giây đầu tiên.
b) Tính quãng đường mà vật di chuyển được trong 2 giây đầu tiên.
Câu hỏi khởi động trang 17 Toán 12 Tập 2
Họa sĩ thiết kế logo hình con cá cho một doanh nghiệp kinh doanh hải sản. Logo là hình phẳng giới hạn bởi hai parabol với các kích thước được cho trong Hình 3 (đơn vị trên mỗi trục tọa độ là decimét).

Làm thế nào để tính diện tích của logo?
Hoạt động 1 trang 17 Toán 12 Tập 2
Cho hàm số y = f(x) = x2. Xét hình phẳng (được tô màu) gồm tất cả các điểm M(x; y) trên mặt phẳng tọa độ sao cho 1 ≤ x ≤ 2 và 0 ≤ y ≤ x2 (Hình 4). Hình phẳng đó được gọi là hình thang cong AMNB giới hạn bởi đồ thị của hàm số f(x) = x2, trục Ox và hai đường thẳng x = 1, x = 2.

Chia đoạn [1; 2] thành n phần bằng nhau bởi các điểm chia:
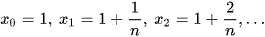
 (Hình 5).
(Hình 5).
a) Tính diện tích T0 của hình chữ nhật dựng trên đoạn [x0; x1] với chiều cao là f(x0).
Tính diện tích T1 của hình chữ nhật dựng trên đoạn [x1; x2] với chiều cao là f(x1).
Tính diện tích T2 của hình chữ nhật dựng trên đoạn [x2; x3] với chiều cao là f(x2).
…
Tính diện tích Tn – 1 của hình chữ nhật dựng trên đoạn [xn – 1; xn] với chiều cao là f(xn–1).

b) Đặt Sn = T0 + T1 + T2 + … + Tn – 1. Chứng minh rằng:
Sn =  .[f(x0) + f(x1) + f(x2) + … + f(xn – 1)].
.[f(x0) + f(x1) + f(x2) + … + f(xn – 1)].
Tổng Sn gọi là tổng tích phân cấp n của hàm số f(x) = x2 trên đoạn [1; 2].
Luyện tập 1 trang 19 Toán 12 Tập 2
Cho đồ thị hàm số y = f(x) = 2x (x ∈ [0; 2]). Xét tam giác vuông OAB giới hạn bởi đồ thị của hàm số f(x) = 2x, trục Ox và đường thẳng x = 2.
a) Tính diện tích tam giác vuông OAB.
b) Giả sử F(x) là một nguyên hàm của f(x) = 2x trên đoạn [0; 2]. Tính F(2) – F(0). Từ đó hãy chứng tỏ rằng Stam giác vuông OAB = F(2) – F(0).
Hoạt động 2 trang 20 Toán 12 Tập 2
Cho hàm số f(x) = x2.
a) Chứng tỏ F(x) =  , G(x) =
, G(x) =  là các nguyên hàm của hàm số f(x) = x2.
là các nguyên hàm của hàm số f(x) = x2.
b) Chứng minh rằng F(b) – F(a) = G(b) – G(a), tức là hiệu số F(b) – F(a) không phụ thuộc việc chọn nguyên hàm.
Bài 1 trang 26 Tán 12 Tập 2
Bài 1 trang 26 Toán 12 Tập 2: Tích phân 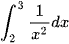 có giá trị bằng:
có giá trị bằng:
Bài 2 trang 26 Toán 12 Tập 2
Bài 2 trang 26 Toán 12 Tập 2: Tích phân 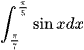 có giá trị bằng:
có giá trị bằng:
Bài 3 trang 26 Toán 12 Tập 2
Bài 3 trang 26 Toán 12 Tập 2: Tích phân  có giá trị bằng:
có giá trị bằng:
A.  .
.
B. 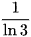 .
.
C. –1.
D. 1.
Bài 4 trang 26 Toán 12 Tập 2
Bài 4 trang 26 Toán 12 Tập 2: Cho 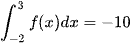 , F(x) là một nguyên hàm của hàm số f(x) trên đoạn [– 2; 3], F(3) = – 8. Tính F(–2).
, F(x) là một nguyên hàm của hàm số f(x) trên đoạn [– 2; 3], F(3) = – 8. Tính F(–2).
 .
. và
và  .
.
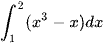 .
. và
và  .
. .
.


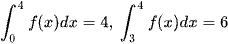 . Tính
. Tính 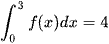 .
.