Giải bài tập Toán 9 Chương 7. Hàm số y = ax² (a ≠ 0). Phương trình bậc hai một ẩn | Cánh Diều
Hướng dẫn giải chi tiết Chương 7. Hàm số y = ax² (a ≠ 0). Phương trình bậc hai một ẩn. Định lí Viète.
Giải bài tập Bài 1. Hàm số y = ax² (a ≠ 0)

Khởi động trang 46 Toán 9 Tập 2:
Hàm số y = 5x2 và đồ thị của hàm số đó có những tính chất như thế nào?

Hoạt động 1 trang 46 Toán 9 Tập 2:
Xét hàm số y = 5x2 trong tình huống ở phần mở đầu.

Luyện tập 1 trang 47 Toán 9 Tập 2:
Hàm số nào sau đây có dạng y = ax2 (a ≠ 0)? Đối với những hàm số đó, xác định hệ số a của x2.

Hoạt động 2 trang 47 Toán 9 Tập 2:
Nêu khái niệm đồ thị của hàm số y = f(x).
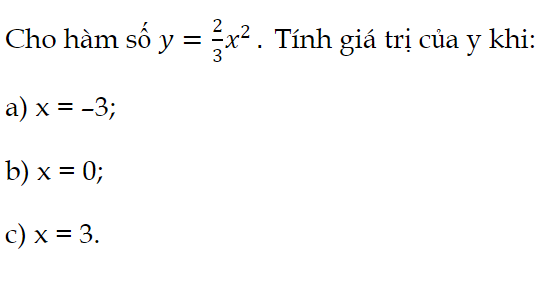
Luyện tập 2 trang 47 Toán 9 Tập 2:
Tính giá trị của y khi:

Hoạt động 3 trang 49 Toán 9 Tập 2:
hãy nêu nhận xét về vị trí cặp điểm E và H; F và G đối với trục Oy.
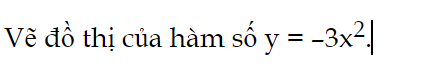
Luyện tập 3 trang 49 Toán 9 Tập 2:
Vẽ đồ thị của hàm số
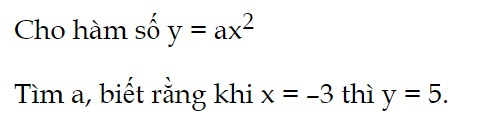
Bài 1 trang 51 Toán 9 Tập 2
Tìm a, biết rằng khi x = –3 thì y = 5.

Bài 2 trang 51 Toán 9 Tập 2:
Tìm giá trị của y tương ứng với giá trị của x trong bảng sau:

Bài 3 trang 51 Toán 9 Tập 2:
Trong mặt phẳng toạ độ Oxy, điểm M(2; –1)

Bài 4 trang 51 Toán 9 Tập 2:
Hàm số y = at2 biểu thị quãng đường (đơn vị: mét) mà một chiếc xe đua đi được trong khoảng thời gian t (giây). Giả sử một chiếc xe đua đi được 125 m sau khoảng thời gian là 5 giây.

Bài 5 trang 51 Toán 9 Tập 2:
Tìm hàm số biểu thị quỹ đạo nhảy của cá heo.

Khởi động trang 52 Toán 9 Tập 2:
Giả sử khi ném một quả bóng vào rổ, độ cao y (feet) của quả bóng và thời gian x (giây) liên hệ với nhau bởi công thức:

Hoạt động 4 trang 10 Toán 12 Tập 1
Gía trị x có phải cực đại cực tiểu của hàm số không. Hoạt động 4 trang 10 Toán 12 Tập 1
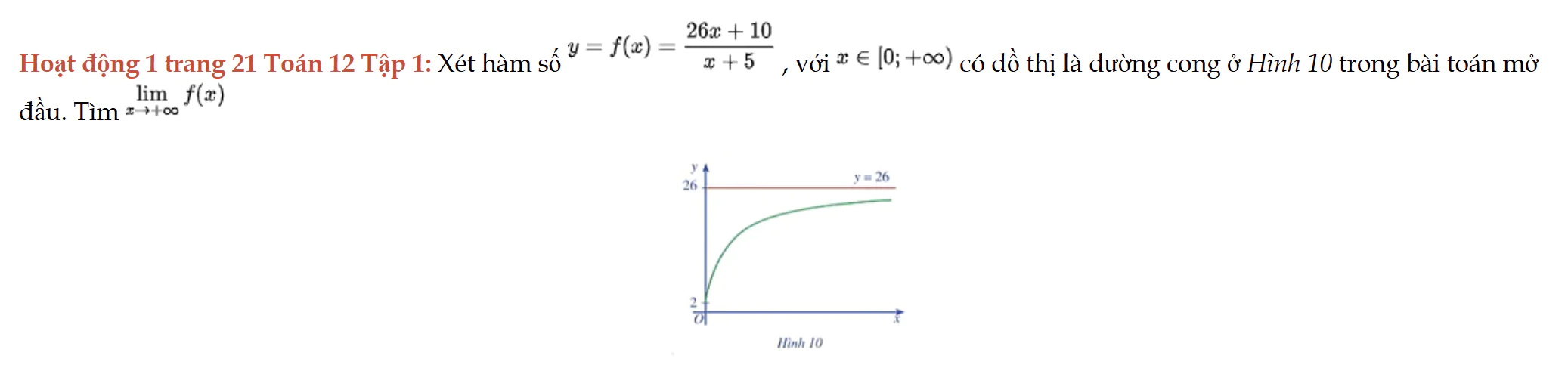
Hoạt động 1 trang 21 Toán 12 Tập 1
Hoạt động 1 trang 21 Toán 12 Tập 1. Quan sát đồ thị, tính lim

Hoạt động 7 trang 9 Toán lớp 10 Tập 1
Hoạt động 7 trang 9 Toán lớp 10 Tập 1: Cho mệnh đề chứa biến “n chia hết cho 3” với n là số tự nhiên. a) Phát biểu “Mọi số tự nhiên n đều chia hết cho 3” có phải là mệnh đề không? b) Phát biểu “Tồn tại số tự nhiên n chia hết cho 3” có phải là mệnh đề k
Giải bài tập Bài 2. Phương trình bậc hai một ẩn.
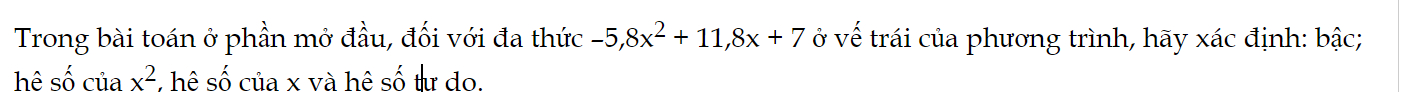
Hoạt động 1 trang 52 Toán 9 Tập 2:
hãy xác định: bậc; hệ số của x2, hệ số của x và hệ số tự do.

Luyện tập 1 trang 52 Toán 9 Tập 2:
Phương trình bậc hai ẩn t;

Hoạt động 2 trang 53 Toán 9 Tập 2:
Giải các phương trình:
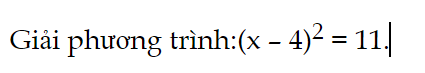
Luyện tập 2 trang 53 Toán 9 Tập 2:
Giải phương trình:

Hoạt động 3 trang 53 Toán 9 Tập 2:
Xét phương trình

Luyện tập 3 trang 55 Toán 9 Tập 2:
Giải các phương trình:

Hoạt động 4 trang 55 Toán 9 Tập 2:
Xét phương trình

Luyện tập 4 trang 56 Toán 9 Tập 2:
Giải các phương trình:
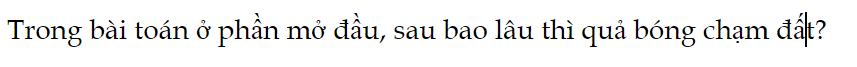
Luyện tập 5 trang 58 Toán 9 Tập 2
Trong bài toán ở phần mở đầu, sau bao lâu thì quả bóng chạm đất?

Luyện tập 6 trang 59 Toán 9 Tập 2:
Sử dụng máy tính cầm tay tìm nghiệm của phương trình bậc hai một ẩn (làm tròn kết quả đến hàng phần mười):

Bài 1 trang 59 Toán 9 Tập 2:
Trong các phương trình sau, phương trình nào là phương trình bậc hai một ẩn?
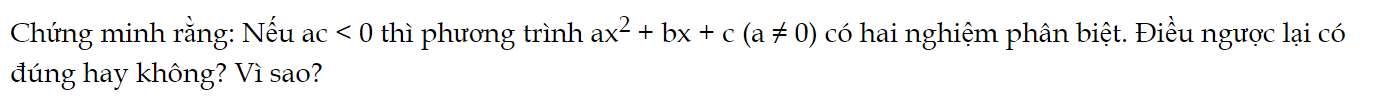
Bài 2 trang 59 Toán 9 Tập 2:
Điều ngược lại có đúng hay không? Vì sao?
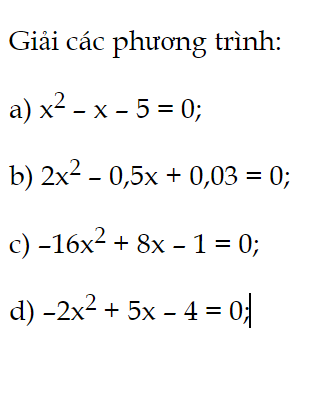
Bài 3 trang 59 Toán 9 Tập 2:
Giải các phương trình:

Bài 4 trang 60 Toán 9 Tập 2:
Ra đa của một máy bay trực thăng theo dõi chuyển động của một ô tô trong 10 phút, phát hiện rằng tốc độ v (km/h) của ô tô thay đổi phụ thuộc vào thời gian t (phút) bởi công thức v = 3t2 – 30t + 135. (Nguồn: Toán 9 – tập 2, NXB Giáo dục Việt Nam, 2020)

Bài 5 trang 60 Toán 9 Tập 2:
Một nhà máy chuyên sản xuất một loại sản phẩm. Năm 2019, nhà máy sản xuất được 5 000 sản phẩm. Do ảnh hưởng của dịch bệnh nên sản lượng của nhà máy trong các năm 2020 và 2021 đều giảm, cụ thể: Số lượng sản phẩm thực tế sản xuất được của năm 2020 giảm x%

Bài 6 trang 60 Toán 9 Tập 2:
Mảnh đất của bác An có dạng hình chữ nhật với chiều dài hơn chiều rộng 10 m. Ở mỗi góc của mảnh đất, bác An đã dành một phần đất có dạng tam giác vuông cân với cạnh góc vuông
Giải bài tập Bài 3. Định lí Viète.

Khởi động trang 61 Toán 9 Tập 2:
Đà Lạt là thành phố du lịch, có khí hậu mát mẻ. Nơi đây trồng nhiều loại hoa để phục vụ nhu cầu trong nước và xuất khẩu. Giả sử người ta trồng hoa trên một mảnh vườn có dạng hình chữ nhật với diện tích là 240 m2, chu vi là 68 m

Hoạt động 1 trang 61 Toán 9 Tập 2:
Xét phương trình
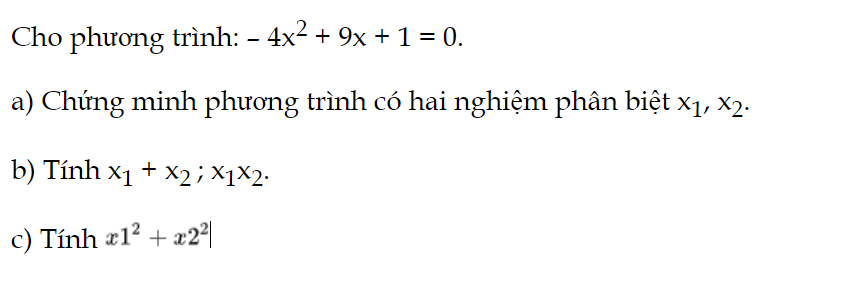
Luyện tập 1 trang 62 Toán 9 Tập 2:
Cho phương trình
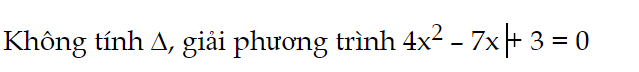
Luyện tập 2 trang 63 Toán 9 Tập 2:
Không tính ∆, giải phương trình

Luyện tập 3 trang 63 Toán 9 Tập 2:
Không tính ∆, giải phương trình

Hoạt động 2 trang 63 Toán 9 Tập 2:
Cho hai số có tổng bằng 5 và tích bằng 6.
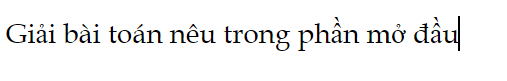
Luyện tập 4 trang 64 Toán 9 Tập 2:
Giải bài toán nêu trong phần mở đầu

Bài 1 trang 64 Toán 9 Tập 2:
Nếu x1, x2 là hai nghiệm của phương trình

Bài 2 trang 64 Toán 9 Tập 2:
Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?
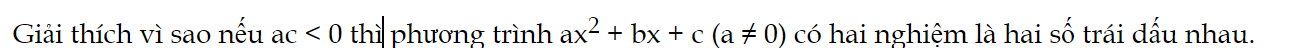
Bài 3 trang 64 Toán 9 Tập 2:
Giải thích vì sao nếu ac < 0

Bài 4 trang 64 Toán 9 Tập 2:
Chứng minh phương trình có hai nghiệm phân biệt x1, x2.

Bài 5 trang 65 Toán 9 Tập 2:
Không tính ∆, giải các phương trình:

Bài 6 trang 65 Toán 9 Tập 2:
Tìm hai số trong mỗi trường hợp sau:

Bài 7 trang 65 Toán 9 Tập 2:
Bác Đạt muốn thiết kế cửa sổ có dạng hình chữ nhật với diện tích bằng 2,52 m2 và chu vi bằng 6,4 m. Tìm các kích thước của cửa sổ đó.
Giải bài tập Bài tập cuối chương 7
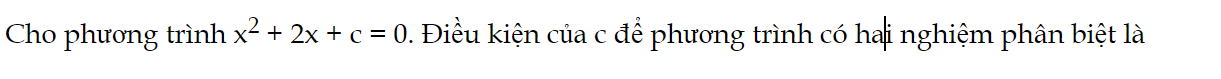
Bài 1 trang 66 Toán 9 Tập 2:
Điều kiện của c để phương trình có hai nghiệm phân biệt là
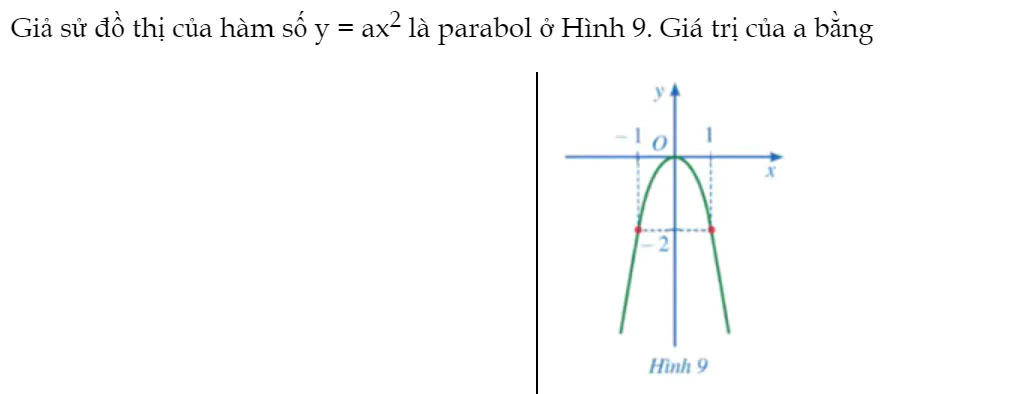
Bài 2 trang 66 Toán 9 Tập 2:
Giả sử đồ thị của hàm số y = ax2 là parabol ở Hình 9. Giá trị của a bằng

Bài 3 trang 66 Toán 9 Tập 2:
Tìm giá trị của y tương ứng với giá trị của x trong bảng sau:
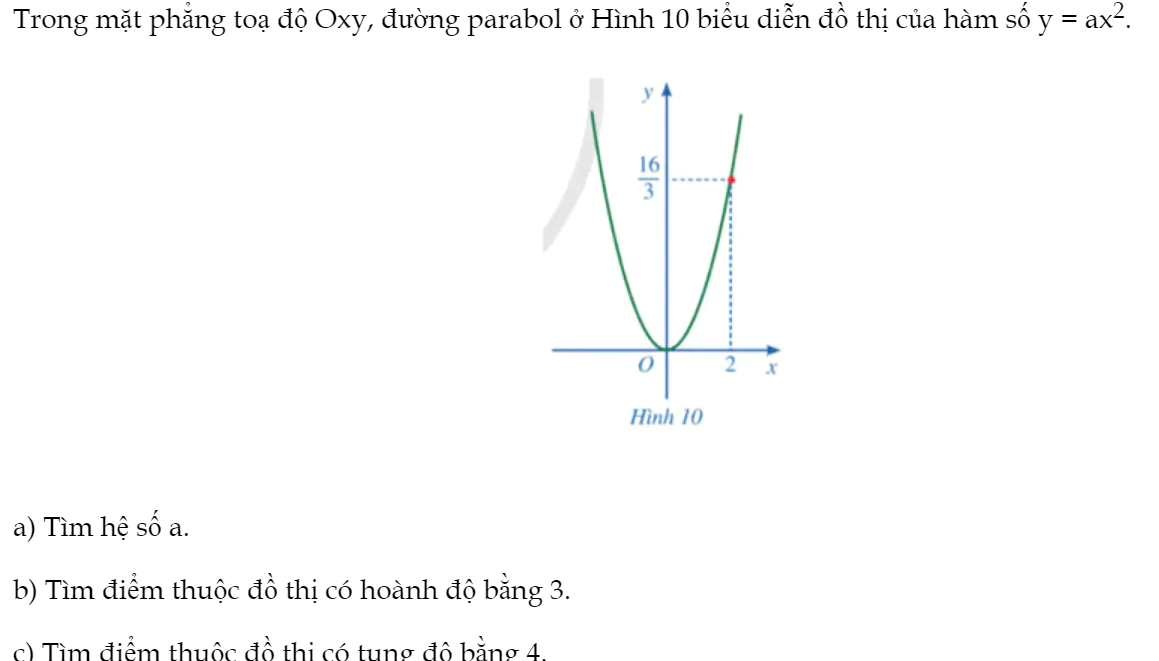
Bài 4 trang 66 Toán 9 Tập 2:
Trong mặt phẳng toạ độ Oxy, đường parabol ở Hình 10 biểu diễn đồ thị của hàm số y = ax2.
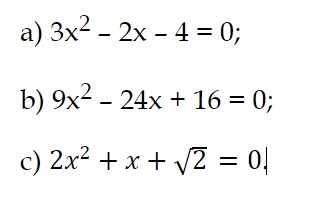
Bài 5 trang 66 Toán 9 Tập 2:
Giải các phương trình:

Bài 6 trang 66 Toán 9 Tập 2:
Không tính ∆, giải các phương trình:
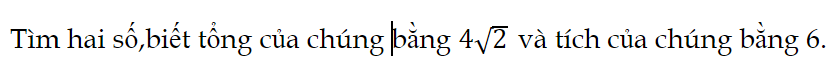
Bài 7 trang 66 Toán 9 Tập 2:
Tìm hai số,
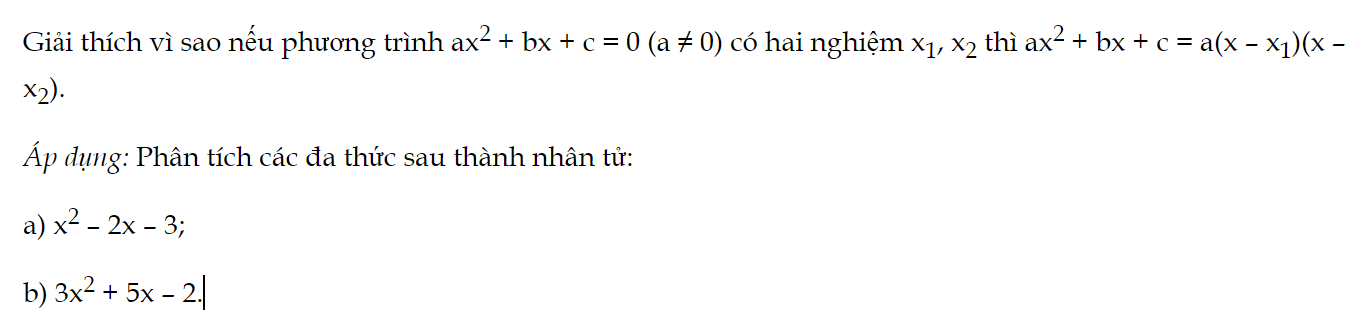
Bài 8 trang 67 Toán 9 Tập 2:
Giải thích vì sao nếu phương trình

Bài 9 trang 67 Toán 9 Tập 2:
Một chiếc áo có giá niêm yết là 120 000 đồng. Để thanh lí chiếc áo, đầu tiên người ta giảm giá x% so với giá niêm yết. Do vẫn chưa bán được chiếc áo nên người ta tiếp tục giảm giá x% so với giá vừa được giảm. Sau hai đợt giảm giá, giá của chiếc áo còn 76

Bài 10 trang 67 Toán 9 Tập 2:
Một công ty sản xuất các khay có dạng hình hộp chữ nhật để trồng rau trong chung cư ở các thành phố. Biết diện tích mặt đáy của khay đó là 2 496 cm2 và chu vi mặt đáy của khay đó là 220 cm. Tìm các kích thước mặt đáy của khay đó.

Bài 11 trang 67 Toán 9 Tập 2:
Cầu Trường Tiền (hay cầu Tràng Tiền) ở thành phố Huế được khởi công vào tháng 5/1899 và khánh thành vào ngày 18/12/1900. Cầu được thiết kế theo kiến trúc Gothic, bắc qua sông Hương. Từ Festival Huế năm 2002, cầu Trường Tiền được lắp đặt một hệ thống chiếu