Giải bài tập Toán 11 Chương 7: Quan hệ vuông góc trong không gian | Kết Nối Tri Thức
Hướng dẫn giải Chương 7: Quan hệ vuông góc trong không gian
Giải bài tập Bài 22: Hai đường thẳng vuông góc

Bài 7.1 trang 30 Toán 11 Tập 2
Cho hình lăng trụ ABC.A'B'C' có đáy là các tam giác đều. Tính góc (AB, B'C'). Bài 7.1 trang 30 Toán 11 Tập 2

Bài 7.2 trang 30 Toán 11 Tập 2
Cho hình hộp ABCD.A'B'C'D' có các cạnh bằng nhau. Chứng minh rằng tứ diện ACB'D' có các cặp cạnh đối diện vuông góc với nhau. Bài 7.2 trang 30 Toán 11 Tập 2

Bài 7.3 trang 30 Toán 11 Tập 2
Cho tứ diện ABCD có góc CBD = 90°. Gọi M, N tương ứng là trung điểm của AB, AD. Chứng minh rằng MN vuông góc với BC. Bài 7.3 trang 30 Toán 11 Tập 2

Bài 7.4 trang 30 Toán 11 Tập 2
Đối với nhà gỗ truyền thống, trong các cấu kiện: hoành, quá giang, xà cái, rui, cột tương ứng được đánh số 1, 2, 3, 4, 5 như trong Hình 7.8, những cặp cấu kiện nào vuông góc với nhau. Bài 7.4 trang 30 Toán 11 Tập 2

Mở đầu trang 11 Toán 11 Tập 2
Đối với các nút giao thông cùng mức hay khác mức, để có thể dễ dàng bố trí các nhánh rẽ và để người tham gia giao thông có góc nhìn đảm bảo an toàn. Mở đầu trang 11 Toán 11 Tập 2

HĐ1 trang 28 Toán 11 Tập 2
Trong không gian, cho hai đường thẳng chéo nhau m và n. Từ hai điểm phân biệt O, O' tuỳ ý lần lượt kẻ các cặp đường thẳng a, b và a', b' tương ứng song song với m, n (H.7.2). HĐ1 trang 28 Toán 11 Tập 2
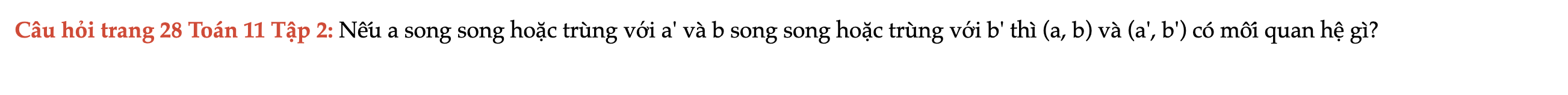
Câu hỏi trang 28 Toán 11 Tập 2
Nếu a song song hoặc trùng với a' và b song song hoặc trùng với b' thì (a, b) và (a', b') có mối quan hệ gì? Câu hỏi trang 28 Toán 11 Tập 2

Vận dụng trang 29 Toán 11 Tập 2
Kim tự tháp Kheops là kim tự tháp lớn nhất trong các kim tự tháp ở Ai Cập, được xây dựng vào thế kỉ thứ 26 trước Công nguyên và là một trong bảy kì quan của thế giới cổ đại. Vận dụng trang 29 Toán 11 Tập 2

HĐ2 trang 29 Toán 11 Tập 2
Đối với hai cánh cửa trong Hình 7.5, tính góc giữa hai đường mép cửa BC và MN. HĐ2 trang 29 Toán 11 Tập 2

Câu hỏi trang 29 Toán 11 Tập 2
Nếu đường thẳng a vuông góc với đường thẳng b thì a có vuông góc với các đường thẳng song song với b hay không? Câu hỏi trang 29 Toán 11 Tập 2

Luyện tập trang 30 Toán 11 Tập 2
Cho tam giác MNP vuông tại N và một điểm A nằm ngoài mặt phẳng (MNP). Lần lượt lấy các điểm B, C, D sao cho M, N, P tương ứng là trung điểm của AB, AC, CD (H.7.7). Luyện tập trang 30 Toán 11 Tập 2
Giải bài tập Bài 23: Đường thẳng vuông góc với mặt phẳng

Bài 7.5 trang 36 Toán 11 Tập 2
Cho hình chóp S.ABC có đáy là tam giác cân tại A và SA ⊥ (ABC). Gọi M là trung điểm của BC. Chứng minh rằng BC ⊥ (SAM). Bài 7.5 trang 36 Toán 11 Tập 2

Bài 7.6 trang 36 Toán 11 Tập 2
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật và SA ⊥ (ABCD). Chứng minh rằng các mặt bên của hình chóp S.ABCD là các tam giác vuông. Bài 7.6 trang 36 Toán 11 Tập 2

Bài 7.7 trang 36 Toán 11 Tập 2
Cho hình chóp S.ABCD có đáy là hình chữ nhật và SA ⊥ (ABCD). Gọi M, N tương ứng là hình chiếu của A trên SB, SD. Chứng minh rằng AM ⊥ (SBC); AN ⊥ (SCD); SC ⊥ (AMN). Bài 7.7 trang 36 Toán 11 Tập 2

Bài 7.8 trang 36 Toán 11 Tập 2
Bạn Vinh thả quả dọi chìm vào thùng nước. Hỏi khi dây dọi căng và mặt nước yên lặng thì đường thẳng chứa dây dọi có vuông góc với mặt phẳng chứa mặt nước trong thùng hay không. Bài 7.8 trang 36 Toán 11 Tập 2

Bài 7.9 trang 36 Toán 11 Tập 2
Một cột bóng rổ được dựng trên một sân phẳng. Bạn Hùng đo khoảng cách từ một điểm trên sân, cách chân cột 1 m đến một điểm trên cột, cách chân cột 1 m được kết quả là 1,5 m (H.7.27). Bài 7.9 trang 36 Toán 11 Tập 2

HĐ1 trang 31 Toán 11 Tập 2
Đối với cánh cửa như trong Hình 7.10, khi đóng – mở cánh cửa, ta coi mép dưới BC của cánh cửa luôn sát sàn nhà (khe hở không đáng kể). HĐ1 trang 31 Toán 11 Tập 2

Câu hỏi trang 32 Toán 11 Tập 2
Nếu đường thẳng ∆ và mặt phẳng (P) vuông góc với nhau thì chúng có cắt nhau hay không? Câu hỏi trang 32 Toán 11 Tập 2

HĐ2 trang 32 Toán 11 Tập 2
Gấp tấm bìa cứng hình chữ nhật sao cho nếp gấp chia tấm bìa thành hai hình chữ nhật, sau đó đặt nó lên mặt bàn như Hình 7.11. HĐ2 trang 32 Toán 11 Tập 2

Câu hỏi trang 32 Toán 11 Tập 2
Nếu một đường thẳng vuông góc với hai cạnh của một tam giác thì đường thẳng đó có vuông góc với cạnh còn lại hay không? Câu hỏi trang 32 Toán 11 Tập 2

Luyện tập 1 trang 32 Toán 11 Tập 2
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O, SA = SC và SB = SD (H.7.14). Chứng minh rằng SO ⊥ (ABCD). Luyện tập 1 trang 32 Toán 11 Tập 2

Vận dụng trang 33 Toán 11 Tập 2
Khi làm cột treo quần áo, ta có thể tạo hai thanh đế thẳng đặt dưới sàn nhà và dựng cột treo vuông góc với hai thanh đế đó (H.7.15). Hãy giải thích vì sao bằng cách đó ta có được cột treo vuông góc với sàn nhà. Vận dụng trang 33 Toán 11 Tập 2

HĐ3 trang 33 Toán 11 Tập 2
Cho điểm O và đường thẳng ∆ không đi qua O. Gọi d là đường thẳng đi qua O và song song với ∆. Xét hai mặt phẳng phân biệt tuỳ ý (P) và (Q) cùng chứa d. HĐ3 trang 33 Toán 11 Tập 2

HĐ4 trang 34 Toán 11 Tập 2
Cho mặt phẳng (P) và điểm O. Trong mặt phẳng (P), lấy hai đường thẳng cắt nhau a, b tuỳ ý. Gọi (α), (β) là các mặt phẳng qua O và tương ứng vuông góc với a, b (H.7.19). HĐ4 trang 34 Toán 11 Tập 2
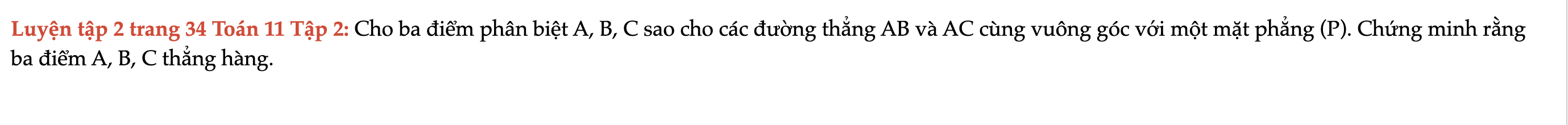
Luyện tập 2 trang 34 Toán 11 Tập 2
Cho ba điểm phân biệt A, B, C sao cho các đường thẳng AB và AC cùng vuông góc với một mặt phẳng (P). Chứng minh rằng ba điểm A, B, C thẳng hàng. Luyện tập 2 trang 34 Toán 11 Tập 2

HĐ5 trang 34 Toán 11 Tập 2
Cho đường thẳng a vuông góc với mặt phẳng (P) và song song với đường thẳng b. Lấy một đường thẳng m bất kì thuộc mặt phẳng (P) (H.7.20). Tính (b, m) và từ đó rút ra mối quan hệ giữa b và (P). HĐ5 trang 34 Toán 11 Tập 2

HĐ6 trang 34 Toán 11 Tập 2
Cho hai đường thẳng phân biệt a và b cùng vuông góc với mặt phẳng (P). Xét O là một điểm thuộc a nhưng không thuộc b. Gọi c là đường thẳng qua O và song song với b (H.7.21). HĐ6 trang 34 Toán 11 Tập 2

HĐ7 trang 35 Toán 11 Tập 2
Cho hai mặt phẳng (P) và (Q) song song với nhau và đường thẳng ∆ vuông góc với (P). Gọi b là một đường thẳng bất kì thuộc (Q). Lấy một đường thẳng a thuộc (P) sao cho a song song với b (H.7.23). HĐ7 trang 35 Toán 11 Tập 2

HĐ8 trang 35 Toán 11 Tập 2
Cho hai mặt phẳng (P) và (Q) cùng vuông góc với đường thẳng ∆. Xét O là một điểm thuộc mặt phẳng (P) nhưng không thuộc mặt phẳng (Q). Gọi (R) là mặt phẳng đi qua O và song song với (Q). (H.7.24). HĐ8 trang 35 Toán 11 Tập 2

Luyện tập 3 trang 35 Toán 11 Tập 2
Một chiếc bàn có các chân cùng vuông góc với mặt phẳng chứa mặt bàn và mặt phẳng chứa mặt sàn. Hỏi hai mặt phẳng đó có song song với nhau hay không? Vì sao? Luyện tập 3 trang 35 Toán 11 Tập 2

HĐ9 trang 35 Toán 11 Tập 2
Cho đường thẳng a song song với mặt phẳng (P) và đường thẳng ∆ vuông góc với mặt phẳng (P). Tính (∆, a). HĐ9 trang 35 Toán 11 Tập 2

HĐ10 trang 36 Toán 11 Tập 2
Cho đường thẳng a và mặt phẳng (P) cùng vuông góc với một đường thẳng ∆. Qua một điểm O thuộc (P), kẻ đường thẳng a' song song với a. Nêu vị trí tương đối giữa a' và (P). HĐ10 trang 36 Toán 11 Tập 2

Luyện tập 4 trang 36 Toán 11 Tập 2
Cho hình chóp S.ABCD có đáy ABCD là một hình vuông, SA ⊥ (ABCD). Kẻ AH vuông góc với SC (H thuộc SC), BM vuông góc với SC (M thuộc SC). Chứng minh rằng SC ⊥ (MBD) và AH // (MBD). Luyện tập 4 trang 36 Toán 11 Tập 2
Giải bài tập Bài 24: Phép chiếu vuông góc. Góc giữa đường thẳng và mặt phẳng

Bài 7.10 trang 42 Toán 11 Tập 2
Cho hình chóp S.ABC có SA ⊥ (ABC), tam giác ABC vuông tại B. Xác định hình chiếu của điểm S trên mặt phẳng (ABC). Bài 7.10 trang 42 Toán 11 Tập 2
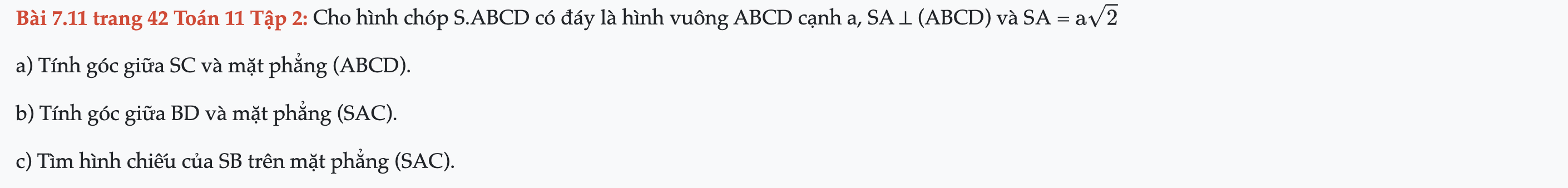
Bài 7.11 trang 42 Toán 11 Tập 2
Cho hình chóp S.ABCD có đáy là hình vuông ABCD cạnh a, SA ⊥ (ABCD) và SA = a căn 2. Tính góc giữa SC và mặt phẳng (ABCD). Bài 7.11 trang 42 Toán 11 Tập 2

Bài 7.12 trang 42 Toán 11 Tập 2
Cho hình chóp S.ABC có SA ⊥ (ABC), tam giác ABC vuông tại B, SA = AB = BC = a. Xác định hình chiếu của A trên mặt phẳng (SBC). Bài 7.12 trang 42 Toán 11 Tập 2

Bài 7.13 trang 43 Toán 11 Tập 2
Cho điểm S nằm ngoài mặt phẳng (P), có hình chiếu H trên (P). Với mỗi đểm M bất kì (không trùng H) trên mặt phẳng (P), ta gọi đoạn thẳng SM là đường xiên, đoạn thẳng HM là hình chiếu trên (P) của đường xiên đó. Bài 7.13 trang 43 Toán 11 Tập 2

Bài 7.14 trang 43 Toán 11 Tập 2
Trong một khoảng thời gian đầu kể từ khi cất cánh, máy bay bay theo một đường thẳng. Góc cất cánh của nó là góc giữa đường thẳng đó và mặt phẳng nằm ngang nơi cất cánh. Bài 7.14 trang 43 Toán 11 Tập 2

Bài 7.15 trang 43 Toán 11 Tập 2
Hãy nêu cách đo góc giữa đường thẳng chứa tia sáng mặt trời và mặt phẳng nằm ngang tại một vị trí và một thời điểm. Bài 7.15 trang 43 Toán 11 Tập 2

Mở đầu trang 38 Toán 11 Tập 2
Vào khoảng thời gian giữa mùa hè, ở phía bắc của vòng Bắc Cực (như một số vùng phía bắc của Na Uy, Phần Lan, Nga,...), Mặt Trời có thể được nhìn thấy trong suốt 24 giờ của ngày. Mở đầu trang 38 Toán 11 Tập 2

HĐ1 trang 38 Toán 11 Tập 2
Trên sân phẳng có một cây cột thẳng vuông góc với mặt sân. Dưới ánh sáng mặt trời, bóng của cây cột trên sân có thể được nhìn như là hình chiếu của cây cột qua một phép chiếu song song hay không? HĐ1 trang 38 Toán 11 Tập 2

Câu hỏi trang 39 Toán 11 Tập 2
Nếu A là một điểm không thuộc mặt phẳng (P) và A' là hình chiếu của A trên (P) thì đường thẳng AA' có quan hệ gì với mặt phẳng (P)? Câu hỏi trang 39 Toán 11 Tập 2

HĐ2 trang 39 Toán 11 Tập 2
Cho đường thẳng a và mặt phẳng (P) không vuông góc với nhau. Xét b là một đường thẳng nằm trong (P). Trên a, lấy hai điểm M, N tùy ý. Gọi M', N' tương ứng là hình chiếu của M, N trên mặt phẳng (P) (H.7.34). HĐ2 trang 39 Toán 11 Tập 2

Luyện tập 1 trang 40 Toán 11 Tập 2
Cho hình chóp S.ABC có SA = SB = SC. Gọi O là hình chiếu của S trên mặt phẳng (ABC) (H.7.36). Chứng minh rằng O là tâm đường tròn ngoại tiếp tam giác ABC. Luyện tập 1 trang 40 Toán 11 Tập 2

HĐ3 trang 40 Toán 11 Tập 2
Một máy bay giữ vận tốc không đổi, với độ lớn 240 km/h trong suốt 2 phút đầu kể từ khi cất cánh. Hỏi thông tin trên có đủ để ta xác định độ cao của máy bay so với mặt đất phẳng. HĐ3 trang 40 Toán 11 Tập 2

Vận dụng trang 42 Toán 11 Tập 2
Tâm Trái Đất chuyển động quanh Mặt Trời theo quỹ đạo là một đường elip nhận tâm Mặt Trời làm tiêu điểm. Trong quá trình chuyển động, Trái Đất lại quay quanh trục Bắc Nam. Vận dụng trang 42 Toán 11 Tập 2

Khám phá trang 42 Toán 11 Tập 2
Cho đường thẳng ∆ vuông góc với mặt phẳng (P). Khi đó, với một đường thẳng a bất kì, góc giữa a và (P) có mối quan hệ gì với góc giữa a và ∆? Khám phá trang 42 Toán 11 Tập 2

Trải nghiệm trang 42 Toán 11 Tập 2
Đo góc giữa một sợi dây kéo căng và mặt bàn hoặc sàn lớp học. (Có thể cho một đầu dây thuộc mặt bàn, mặt sàn để thuận tiện hơn cho việc đo). Trải nghiệm trang 42 Toán 11 Tập 2
Giải bài tập Bài 25: Hai mặt phẳng vuông góc

Bài 7.16 trang 53 Toán 11 Tập 2
Cho hình chóp S.ABC có SA ⊥ (ABC). Gọi H là hình chiếu của A trên BC. Chứng minh rằng (SAB) ⊥ (ABC) và (SAH) ⊥ (SBC). Bài 7.16 trang 53 Toán 11 Tập 2

Bài 7.17 trang 53 Toán 11 Tập 2
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Tính độ dài đường chéo của hình lập phương. Bài 7.17 trang 53 Toán 11 Tập 2
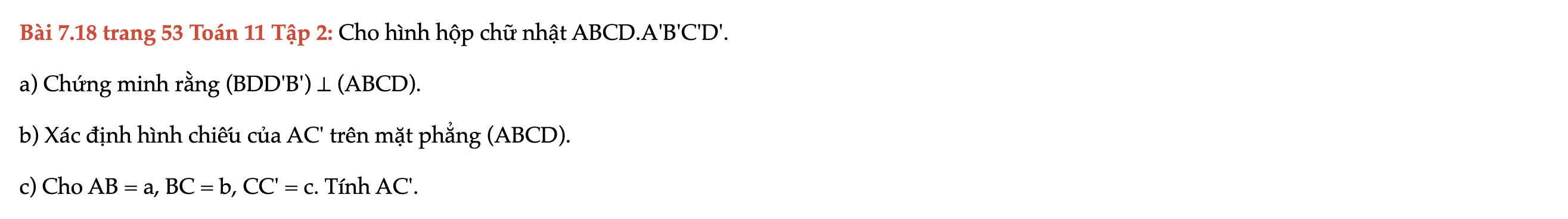
Bài 7.18 trang 53 Toán 11 Tập 2
Cho hình hộp chữ nhật ABCD.A'B'C'D'. Chứng minh rằng (BDD'B') ⊥ (ABCD). Bài 7.18 trang 53 Toán 11 Tập 2

Bài 7.19 trang 53 Toán 11 Tập 2
Cho hình chóp đều S.ABC, đáy có cạnh bằng a, cạnh bên bằng b. Tính sin của góc tạo bởi cạnh bên và mặt đáy. Bài 7.19 trang 53 Toán 11 Tập 2

Bài 7.20 trang 53 Toán 11 Tập 2
Hai mái nhà trong Hình 7.72 là hai hình chữ nhật. Giả sử AB = 4,8 m; OA = 2,8 m; OB = 4 m. Tính (gần đúng) số đo của góc nhị diện tạo bởi hai nửa mặt phẳng tương ứng chứa hai mái nhà. Bài 7.20 trang 53 Toán 11 Tập 2

Bài 7.21 trang 53 Toán 11 Tập 2
Độ dốc của mái nhà, mặt sân, con đường thẳng là tang của góc tạo bởi mái nhà, mặt sân, con đường thẳng đó với mặt phẳng nằm ngang. Độ dốc của đường thẳng dành cho người khuyết tật được quy định là không quá 1/12. Bài 7.21 trang 53 Toán 11 Tập 2

HĐ1 trang 44 Toán 11 Tập 2
Cho hai mặt phẳng (P) và (Q). Lấy hai đường thẳng a, a' cùng vuông góc với (P), hai đường thẳng b, b' cùng vuông góc với (Q). Tìm mối quan hệ giữa các góc (a, b) và (a', b'). HĐ1 trang 44 Toán 11 Tập 2
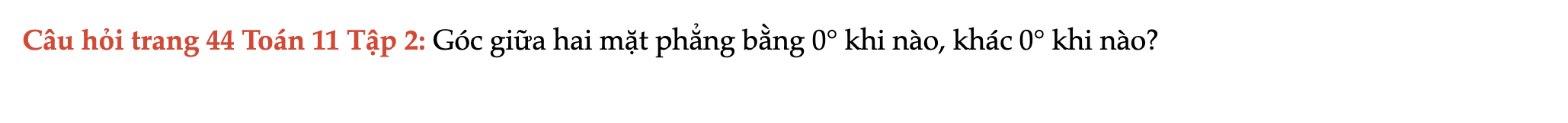
Câu hỏi trang 44 Toán 11 Tập 2
Góc giữa hai mặt phẳng bằng 0° khi nào, khác 0° khi nào? Câu hỏi trang 44 Toán 11 Tập 2

Luyện tập 1 trang 45 Toán 11 Tập 2
Cho hình chóp S.ABCD, đáy ABCD là một hình chữ nhật có tâm O, SO ⊥ (ABCD). Chứng minh rằng hai mặt phẳng (SAC) và (SBD) vuông góc với nhau khi và chỉ khi ABCD là một hình vuông. Luyện tập 1 trang 45 Toán 11 Tập 2

HĐ2 trang 45 Toán 11 Tập 2
Cho mặt phẳng (P) chứa đường thẳng b vuông góc với mặt phẳng (Q). Lấy một đường thẳng a vuông góc với (P). (H.7.47). HĐ2 trang 45 Toán 11 Tập 2
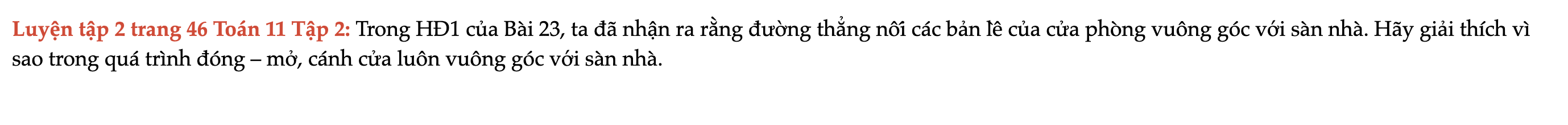
Luyện tập 2 trang 46 Toán 11 Tập 2
Trong HĐ1 của Bài 23, ta đã nhận ra rằng đường thẳng nối các bản lề của cửa phòng vuông góc với sàn nhà. Hãy giải thích vì sao trong quá trình đóng – mở, cánh cửa luôn vuông góc với sàn nhà. Luyện tập 2 trang 46 Toán 11 Tập 2

HĐ3 trang 46 Toán 11 Tập 2
Cho hai mặt phẳng (P) và (Q) vuông góc với nhau. Kẻ đường thẳng a thuộc (P) và vuông góc với giao tuyến ∆ của (P) và (Q). Gọi O là giao điểm của a và ∆. HĐ3 trang 46 Toán 11 Tập 2

HĐ4 trang 46 Toán 11 Tập 2
Cho hai mặt phẳng (P) và (Q) cắt nhau theo giao tuyến a và cùng vuông góc với mặt phẳng (R). Gọi O là một điểm thuộc a và a' là đường thẳng qua O và vuông góc với (R). HĐ4 trang 46 Toán 11 Tập 2

Luyện tập 3 trang 47 Toán 11 Tập 2
Với giả thiết như ở Ví dụ 3, Cho hình chóp S.ABCD có đáy là hình chữ nhật và SA ⊥ (ABCD). Gọi B', C', D' tương ứng là hình chiếu của A trên SB, SC, SD. Luyện tập 3 trang 47 Toán 11 Tập 2

HĐ5 trang 47 Toán 11 Tập 2
Một tài liệu hướng dẫn rằng đối với ghế bàn ăn, nên thiết kế lưng ghế tạo với mặt ghế một góc có số đo từ 100° đến 105°. Trong hình 7.51, các tia Ox, Oy được vẽ tương ứng trên mặt ghế. HĐ5 trang 47 Toán 11 Tập 2
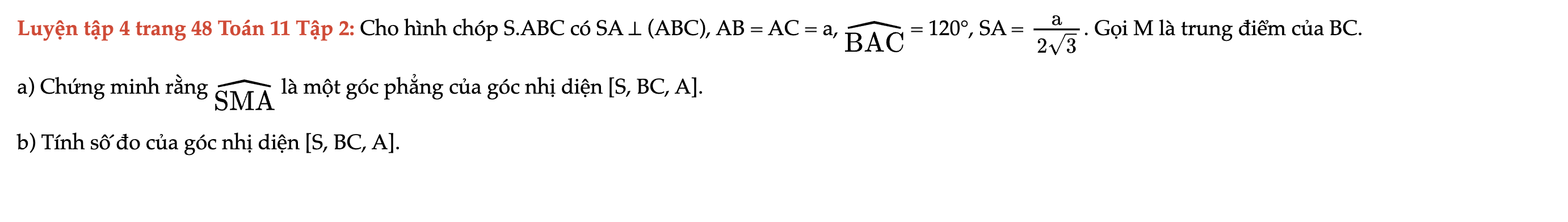
Luyện tập 4 trang 48 Toán 11 Tập 2
Luyện tập 4 trang 48 Toán 11 Tập 2

Vận dụng 1 trang 48 Toán 11 Tập 2
Trong cửa sổ ở Hình 7.56, cánh và khung cửa là các nửa hình tròn có đường kính 80 cm, bản lề được đính ở điểm chính giữa O của các cung tròn khung và cánh cửa. Vận dụng 1 trang 48 Toán 11 Tập 2

HĐ6 trang 49 Toán 11 Tập 2
Các mặt bên của lăng trụ đứng là các hình gì và các mặt bên đó có vuông góc với mặt đáy không? Vì sao? HĐ6 trang 49 Toán 11 Tập 2

HĐ7 trang 49 Toán 11 Tập 2
Các mặt bên của hình lăng trụ đều có phải là các hình chữ nhật có cùng kích thước hay không? Vì sao? HĐ7 trang 49 Toán 11 Tập 2

HĐ8 trang 49 Toán 11 Tập 2
Trong 6 mặt của hình hộp đứng, có ít nhất bao nhiêu mặt là hình chữ nhật? Vì sao? HĐ8 trang 49 Toán 11 Tập 2

HĐ9 trang 50 Toán 11 Tập 2
Hình hộp chữ nhật có bao nhiêu mặt là hình chữ nhật? Vì sao? Các đường chéo của hình hộp chữ nhật có bằng nhau và cắt nhau tại trung điểm mỗi đường hay không? Vì sao? HĐ9 trang 50 Toán 11 Tập 2

HĐ10 trang 50 Toán 11 Tập 2
Các mặt của một hình lập phương là các hình gì? Vì sao? HĐ10 trang 50 Toán 11 Tập 2

Vận dụng 2 trang 50 Toán 11 Tập 2
Từ một tấm tôn hình chữ nhật, tại 4 góc bác Hùng cắt bỏ đi 4 hình vuông có cùng kích thước và sau đó hàn gắn các mép tại các góc như Hình 7.65. Vận dụng 2 trang 50 Toán 11 Tập 2

HĐ11 trang 51 Toán 11 Tập 2
Tháp lớn tại Bảo tàng Louvre ở Paris (H.7.66) (với kết cấu kính và kim loại) có dạng hình chóp với đáy là hình vuông có cạnh bằng 34 m, các cạnh bên bằng nhau và có độ dài xấp xỉ 32,3 m. HĐ11 trang 51 Toán 11 Tập 2

HĐ12 trang 51 Toán 11 Tập 2
Cho hình chóp S.A1A2...An. Gọi O là hình chiếu của S trên mặt phẳng (A1A2...An) (H.7.67). Trong trường hợp hình chóp đã cho là đều, vị trí của điểm O có gì đặc biệt đối với đa giác đều A1A2...An? HĐ12 trang 51 Toán 11 Tập 2
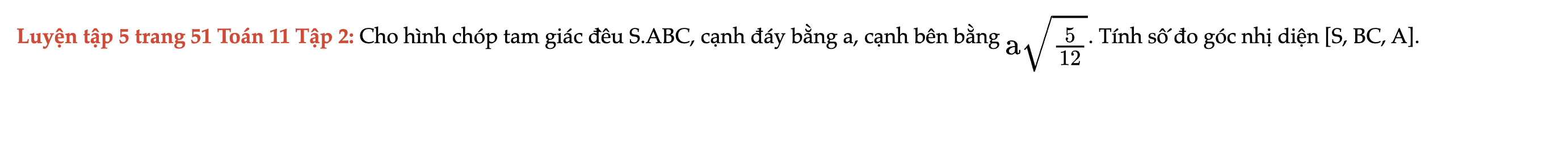
Luyện tập 5 trang 51 Toán 11 Tập 2
Cho hình chóp tam giác đều S.ABC, cạnh đáy bằng a, cạnh bên có số đo như sau. Tính số đo góc nhị diện [S, BC, A]. Luyện tập 5 trang 51 Toán 11 Tập 2

HĐ13 trang 52 Toán 11 Tập 2
HĐ13 trang 52 Toán 11 Tập 2

Câu hỏi trang 52 Toán 11 Tập 2
Hình chóp cụt đều có các cạnh bên bằng nhau hay không? Câu hỏi trang 52 Toán 11 Tập 2
Giải bài tập Bài 26: Khoảng cách

Bài 7.22 trang 59 Toán 11 Tập 2
Cho hình chóp S.ABCD có đáy là một hình vuông cạnh a, mặt bên SAD là một tam giác đều và (SAD) ⊥ (ABCD). Tính chiều cao của hình chóp. Bài 7.22 trang 59 Toán 11 Tập 2
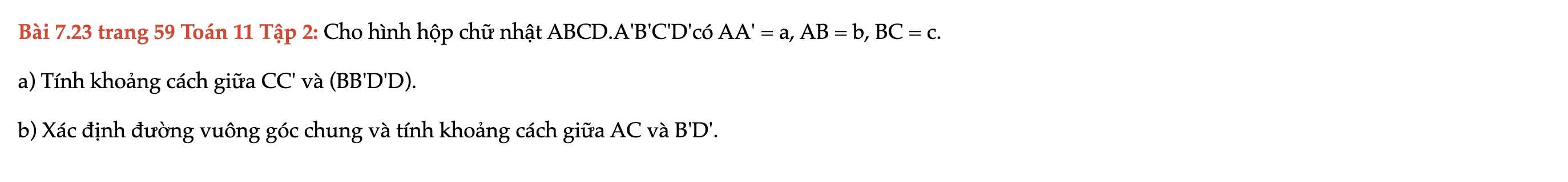
Bài 7.23 trang 59 Toán 11 Tập 2
Cho hình hộp chữ nhật ABCD.A'B'C'D'có AA' = a, AB = b, BC = c. Tính khoảng cách giữa CC' và (BB'D'D). Bài 7.23 trang 59 Toán 11 Tập 2

Bài 7.24 trang 59 Toán 11 Tập 2
Cho tứ diện ABCD có các cạnh đều bằng a. Gọi M, N tương ứng là trung điểm của các cạnh AB, CD. Chứng minh rằng MN là đường vuông góc chung của AB và CD. Bài 7.24 trang 59 Toán 11 Tập 2

Bài 7.26 trang 59 Toán 11 Tập 2
Giá đỡ ba chân ở Hình 7.90 đang được mở sao cho ba gốc chân cách đều nhau một khoảng cách bằng 110 cm. Tính chiều cao của giá đõ, biết các chân của giá đỡ dài 129 cm. Bài 7.26 trang 59 Toán 11 Tập 2

Bài 7.27 trang 59 Toán 11 Tập 2
Một bể nước có đáy thuộc mặt phẳng nằm ngang. Trong trường hợp này, độ sâu của bể là khoảng cách giữa mặt nước và đáy bể. Bài 7.27 trang 59 Toán 11 Tập 2

Bài 7.25 trang 59 Toán 11 Tập 2
Cho hình lập phương ABCD.A'B'C'D'có cạnh a. Chứng minh rằng hai mặt phẳng (D'AC)và (BC'A') song song với nhau và DB' vuông góc với hai mặt phẳng đó. Bài 7.25 trang 59 Toán 11 Tập 2
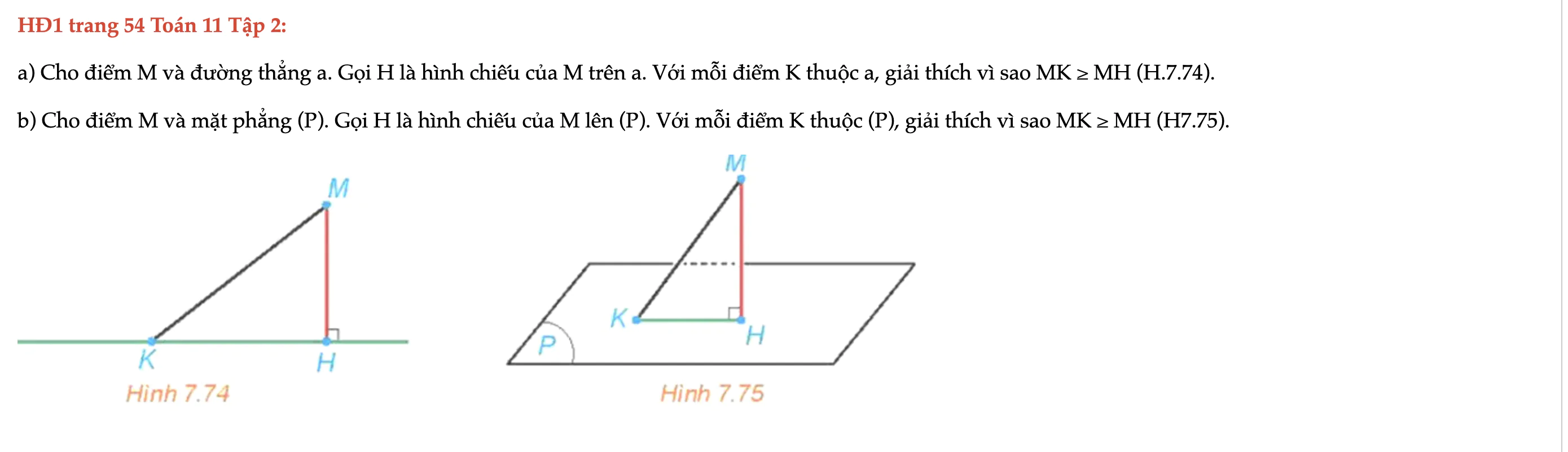
HĐ1 trang 54 Toán 11 Tập 2
Cho điểm M và đường thẳng a. Gọi H là hình chiếu của M trên a. Với mỗi điểm K thuộc a, giải thích vì sao MK ≥ MH (H.7.74). HĐ1 trang 54 Toán 11 Tập 2

Luyện tập 1 trang 55 Toán 11 Tập 2
Cho hình lăng trụ đứng ABC.A'B'C' có ABC là tam giác vuông cân tại A, AB = a, AA' = h (H.7.77). Tính khoảng cách từ A đến mặt phẳng (BCC'B'). Luyện tập 1 trang 55 Toán 11 Tập 2

HĐ2 trang 55 Toán 11 Tập 2
Cho đường thẳng a song song với mặt phẳng (P). Lấy hai điểm M; N bất kỳ thuộc a và gọi A; B tương ứng là các hình chiếu của chúng trên (P) (H.7.78). HĐ2 trang 55 Toán 11 Tập 2

HĐ3 trang 56 Toán 11 Tập 2
Cho hai đường thẳng m và n song song với nhau. Khi một điểm M thay đổi trên m thì khoảng cách từ nó đến đường thẳng n có thay đổi hay không? HĐ3 trang 56 Toán 11 Tập 2

Câu hỏi trang 56 Toán 11 Tập 2
Nếu đường thẳng a thuộc mặt phẳng (P) và mặt phẳng (Q) song song với (P) thì giữa d(a, (Q)) và d((P), (Q)) có mối quan hệ gì? Câu hỏi trang 56 Toán 11 Tập 2

Luyện tập 2 trang 56 Toán 11 Tập 2
Cho hình chóp S.ABC có SA ⊥ (ABC), SA = h. Gọi M, N, P tương ứng là trung điểm của SA, SB, SC. Tính d((MNP), (ABC)) và d(NP, (ABC)). Luyện tập 2 trang 56 Toán 11 Tập 2

Vận dụng 1 trang 57 Toán 11 Tập 2
Ở một con dốc lên cầu, người ta đặt một khung khống chế chiều cao, hai cột của khung có phương thẳng đứng và có chiều dài bằng 2,28 m. Vận dụng 1 trang 57 Toán 11 Tập 2

HĐ4 trang 57 Toán 11 Tập 2
Cho hai đường thẳng chéo nhau a và b. Gọi (Q) là mặt phẳng chứa đường thẳng b và song song với a. Hình chiếu a' của a trên (Q) cắt b tại N. Gọi M là hình chiếu của N trên a (H.7.83). HĐ4 trang 57 Toán 11 Tập 2

Khám phá trang 58 Toán 11 Tập 2
Cho đường thẳng a vuông góc với mặt phẳng (P) và cắt (P) tại O. Cho đường thẳng b thuộc mặt phẳng (P). Hãy tìm mối quan hệ giữa khoảng cách giữa a, b và khoảng cách từ O đến b (H.7.88). Khám phá trang 58 Toán 11 Tập 2

Luyện tập 3 trang 58 Toán 11 Tập 2
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA ⊥ (ABCD), SA = a căn 2. Tính khoảng cách từ A đến SC. Luyện tập 3 trang 58 Toán 11 Tập 2

Thảo luận trang 58 Toán 11 Tập 2
Khoảng cách giữa hai hình được nêu trong bài học (điểm, đường thẳng, mặt phẳng) là khoảng cách nhỏ nhất giữa một điểm thuộc hình này và một điểm thuộc hình kia. Hãy thảo luận để làm rõ nhận xét này. Thảo luận trang 58 Toán 11 Tập 2
Giải bài tập Bài 27: Thể tích
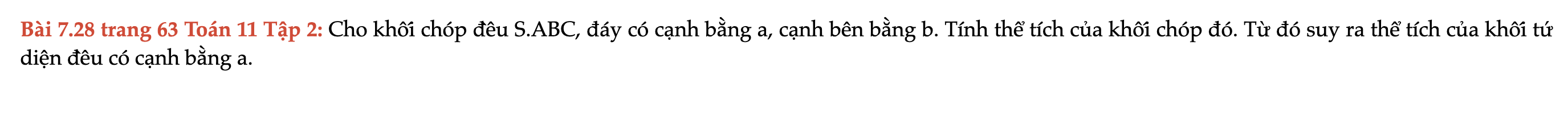
Bài 7.28 trang 63 Toán 11 Tập 2
Cho khối chóp đều S.ABC, đáy có cạnh bằng a, cạnh bên bằng b. Tính thể tích của khối chóp đó. Từ đó suy ra thể tích của khối tứ diện đều có cạnh bằng a. Bài 7.28 trang 63 Toán 11 Tập 2
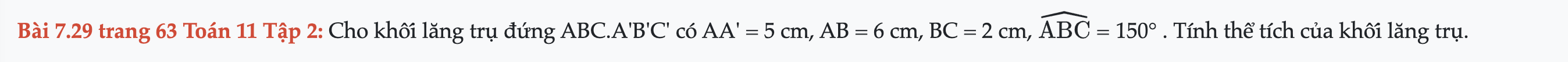
Bài 7.29 trang 63 Toán 11 Tập 2
Cho khối lăng trụ đứng ABC.A'B'C' có AA' = 5 cm, AB = 6 cm, BC = 2 cm, góc ABC = 150° . Tính thể tích của khối lăng trụ. Bài 7.29 trang 63 Toán 11 Tập 2

Bài 7.30 trang 63 Toán 11 Tập 2
Cho khối chóp đều S.ABCD, đáy có cạnh 6 cm. Tính thể tích của khối chóp đó trong các trường hợp sau cạnh bên tạo với mặt đáy một góc bằng 60°. Bài 7.30 trang 63 Toán 11 Tập 2

Bài 7.31 trang 63 Toán 11 Tập 2
Cho khối lăng trụ ABC.A'B'C' có đáy là các tam giác đều cạnh a, A'A = A'B = A'C = b. Tính thể tích của khối lăng trụ. Bài 7.31 trang 63 Toán 11 Tập 2
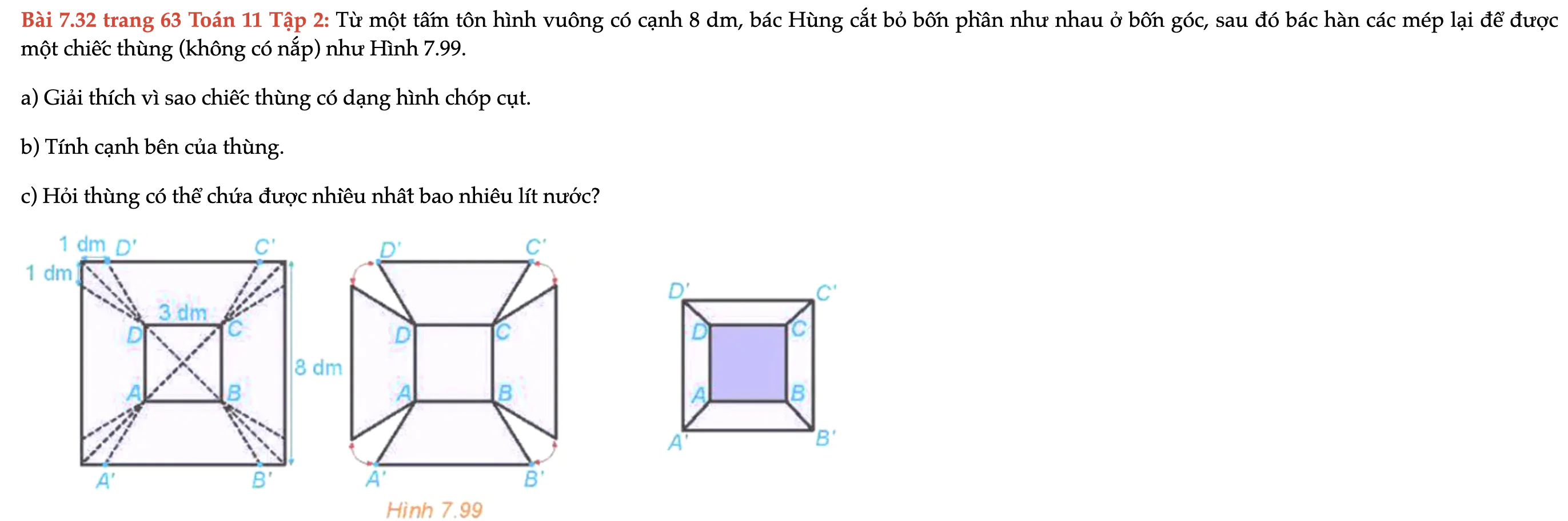
Bài 7.32 trang 63 Toán 11 Tập 2
Từ một tấm tôn hình vuông có cạnh 8 dm, bác Hùng cắt bỏ bốn phần như nhau ở bốn góc, sau đó bác hàn các mép lại để được một chiếc thùng (không có nắp) như Hình 7.99. Bài 7.32 trang 63 Toán 11 Tập 2

HĐ1 trang 61 Toán 11 Tập 2
Khi mua máy điều hòa, bác An được hướng dẫn rằng mỗi mét khối của phòng cần công suất điều hòa 200 BTU. Căn phòng bác An cần lắp máy có dạng hình hộp chữ nhật, rộng 4m, dài 5m và cao 3m. HĐ1 trang 61 Toán 11 Tập 2
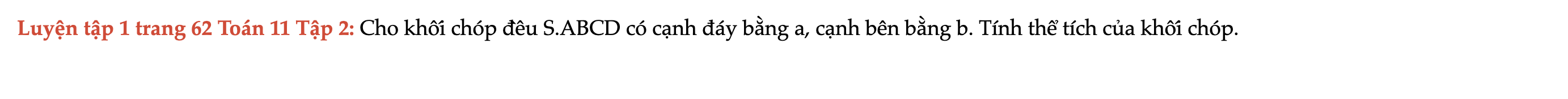
Luyện tập 1 trang 62 Toán 11 Tập 2
Cho khối chóp đều S.ABCD có cạnh đáy bằng a, cạnh bên bằng b. Tính thể tích của khối chóp. Luyện tập 1 trang 62 Toán 11 Tập 2

Luyện tập 2 trang 62 Toán 11 Tập 2
Cho khối chóp cụt đều ABC.A'B'C' có đường cao HH' = h, hai mặt đáy ABC, A'B'C' có cạnh tương ứng bằng 2a, a. Tính thể tích khối chóp cụt. Luyện tập 2 trang 62 Toán 11 Tập 2

Vận dụng trang 63 Toán 11 Tập 2
Một sọt đựng đồ có dạng hình chóp cụt đều (H.7.98). Đáy và miệng sọt là các hình vuông tương ứng có cạnh bằng 30 cm, 60 cm, cạnh bên của sọt dài 50 cm. Tính thể tích của sọt. Vận dụng trang 63 Toán 11 Tập 2
Giải bài tập Bài tập cuối chương 7

Bài 7.33 trang 64 Toán 11 Tập 2
Cho các phát biểu sau. Số phát biểu đúng trong các phát biểu trên là. Bài 7.33 trang 64 Toán 11 Tập 2

Bài 7.34 trang 64 Toán 11 Tập 2
Cho mặt phẳng (P) vuông góc với mặt phẳng (Q) và a là giao tuyến của (P) và (Q). Trong các phát biểu dưới đây, phát biểu nào đúng. Bài 7.34 trang 64 Toán 11 Tập 2

Bài 7.35 trang 64 Toán 11 Tập 2
Cho hình chóp tứ giác đều S.ABCD. Phát biểu nào sau đây là đúng. Bài 7.35 trang 64 Toán 11 Tập 2

Bài 7.36 trang 64 Toán 11 Tập 2
Cho hình chóp S.ABCD có đáy ABCD là hình vuông và SA ⊥ (ABCD). Phát biểu nào sau đây là sai. Bài 7.36 trang 64 Toán 11 Tập 2

Bài 7.37 trang 64 Toán 11 Tập 2
Thể tích của khối chóp có diện tích đáy bằng S, chiều cao bằng h là. Bài 7.37 trang 64 Toán 11 Tập 2

Bài 7.38 trang 65 Toán 11 Tập 2
Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau và OA = a, OB = a căn 2 và OC = 2a. Tính khoảng cách từ điểm O đến mặt phẳng ABC. Bài 7.38 trang 65 Toán 11 Tập 2

Bài 7.39 trang 65 Toán 11 Tập 2
Cho tứ diện ABCD có tam giác ABC cân tại A, tam giác BCD cân tại D. Gọi I là trung điểm của cạnh BC. Chứng minh rằng BC ⊥ (AID). Bài 7.39 trang 65 Toán 11 Tập 2

Bài 7.40 trang 65 Toán 11 Tập 2
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, BC = a và góc CAB = 30°. Biết SA ⊥ (ABC) và SA = a căn 2. Bài 7.40 trang 65 Toán 11 Tập 2

Bài 7.41 trang 65 Toán 11 Tập 2
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a. Biết tam giác SAD vuông cân tại S và (SAD) ⊥ (ABCD). Tính theo a thể tích của khối chóp S.ABCD. Bài 7.41 trang 65 Toán 11 Tập 2

Bài 7.42 trang 65 Toán 11 Tập 2
Cho hình hộp ABCD.A'B'C'D' có độ dài tất cả các cạnh bằng a, AA' ⊥ (ABCD) và góc BAD = 60°. Bài 7.42 trang 65 Toán 11 Tập 2

Bài 7.43 trang 65 Toán 11 Tập 2
Cho hình lăng trụ ABCD.A'B'C'D'. Biết A'.ABCD là hình chóp đều có tất cả các cạnh đều bằng nhau và bằng a. Tính theo a thể tích của khối lăng trụ ABCD.A'B'C'D' và thể tích của khối chóp A'.BB'C'C. Bài 7.43 trang 65 Toán 11 Tập 2

Bài 7.44 trang 65 Toán 11 Tập 2
Cho hình chóp S.ABCD có đáy ABCD là hình thang cân, AB // CD và AB = BC = DA = a, CD = 2a. Biết hai mặt phẳng (SAC) và (SBD) cùng vuông góc với mặt phẳng đáy (ABCD) và SA = a căn 2. Bài 7.44 trang 65 Toán 11 Tập 2

Bài 7.45 trang 65 Toán 11 Tập 2
Trên mặt đất phẳng, người ta dựng một cây cột AB có chiều dài bằng 10 m và tạo với mặt đất góc 80°. Tại một thời điểm dưới ánh sáng mặt trời, bóng BC của cây cột trên mặt đất dài 12 m vào tạo với cây cột một góc bằng 120°. Bài 7.45 trang 65 Toán 11 Tập 2