Giải bài tập Bài 7.38 trang 65 Toán 11 Tập 2 | Toán 11 - Kết nối tri thức
Hướng dẫn giải chi tiết từng bước bài tập Bài 7.38 trang 65 Toán 11 Tập 2. Bài tập cuối chương 7. Toán 11 - Kết nối tri thức
Đề bài:
Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau và OA = a, 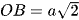OB = và OC = 2a. Tính khoảng cách từ điểm O đến mặt phẳng ABC.
Đáp án và cách giải chi tiết:
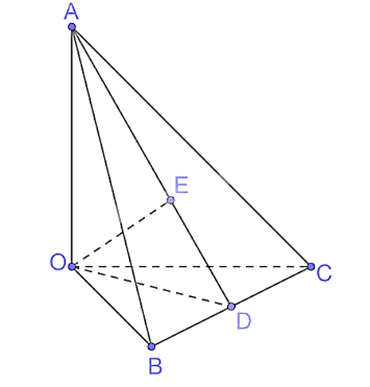
Kẻ OD BC tại D.
Có OA OB, OA OC nên OA (OBC), suy ra OA BC mà OD BC nên
BC (OAD).
Kẻ OE AD tại E.
Vì BC (OAD) nên BC OE mà OE AD nên OE (ABC).
Do đó d(O, (ABC)) = OE.
Xét tam giác OBC vuông tại O, OD là đường cao có:
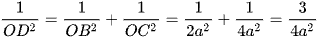
Vì OA (OBC) nên OA OD.
Xét tam giác AOD vuông tại O, OE là đường cao nên
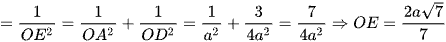
Vậy 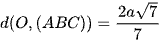d(O, (ABC))
Nguồn: loigiaitoan.com
Tổng số đánh giá:
Xếp hạng: / 5 sao
Bài tập liên quan:
Bài 7.33 trang 64 Toán 11 Tập 2
Cho các phát biểu sau:
(1) (P) và (Q) có giao tuyến là đường thẳng a và cùng vuông góc với mặt phẳng (R) thì a (R).
(2) Hai mặt phẳng (P) và (Q) vuông góc với nhau và có giao tuyến là đường thẳng a, một đường thẳng b nằm trong mặt phẳng (P) và vuông góc với đường thẳng a thì b (Q).
(3) Mặt phẳng (P) chứa đường thẳng a và a vuông góc với (Q) thì (P) (Q).
(4) Đường thẳng a nằm trong mặt phẳng (P) và mặt phẳng (P) vuông góc với mặt phẳng (Q) thì a (Q).
Số phát biểu đúng trong các phát biểu trên là:
A. 1.
B. 2.
C. 3.
D. 4.
Bài 7.34 trang 64 Toán 11 Tập 2
Cho mặt phẳng (P) vuông góc với mặt phẳng (Q) và a là giao tuyến của (P) và (Q). Trong các phát biểu dưới đây, phát biểu nào đúng?
A. Đường thẳng d nằm trên (Q) thì d vuông góc với (P).
B. Đường thẳng d nằm trên (Q) và d vuông góc với a thì d vuông góc với (P).
C. Đường thẳng d vuông góc với a thì d vuông góc với (P).
D. Đường thẳng d vuông góc với (Q) thì d vuông góc với (P).
Bài 7.35 trang 64 Toán 11 Tập 2
Cho hình chóp tứ giác đều S.ABCD. Phát biểu nào sau đây là đúng?
A. Số đo của góc nhị diện [S, AB, C] bằng .
B. Số đo của góc nhị diện [D, SA, B] bằng 90°.
C. Số đo của góc nhị diện [S, AC, B] bằng 90°.
D. Số đo của góc nhị diện [D, SA, B] bằng .
Bài 7.36 trang 64 Toán 11 Tập 2
Cho hình chóp S.ABCD có đáy ABCD là hình vuông và SA (ABCD). Phát biểu nào sau đây là sai?
A. Đường thẳng BC vuông góc với mặt phẳng (SAB).
B. Đường thẳng BD vuông góc với mặt phẳng (SAC).
C. Đường thẳng AC vuông góc với mặt phẳng (SBD).
D. Đường thẳng AD vuông góc với mặt phẳng (SAB).
Bài 7.37 trang 64 Toán 11 Tập 2
Thể tích của khối chóp có diện tích đáy bằng S, chiều cao bằng h là:
A. V = S.h.
B. V = .S.h.
C. V = .S.h.
D. V = .S.h.
Bài 7.39 trang 65 Toán 11 Tập 2
Cho tứ diện ABCD có tam giác ABC cân tại A, tam giác BCD cân tại D. Gọi I là trung điểm của cạnh BC.
a) Chứng minh rằng BC (AID).
b) Kẻ đường cao AH của tam giác AID. Chứng minh rằng AH (BCD).
c) Kẻ đường cao IJ của tam giác AID. Chứng minh rằng IJ là đường vuông góc chung của AD và BC.
Bài 7.40 trang 65 Toán 11 Tập 2
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, BC = a và 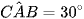= 30o. Biết SA (ABC) và SA = .
a) Chứng minh rằng (SBC) (SAB).
b) Tính theo a khoảng cách từ điểm A đến đường thẳng SC và khoảng cách từ điểm A đến mặt phẳng (SBC).
Bài 7.41 trang 65 Toán 11 Tập 2
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a. Biết tam giác SAD vuông cân tại S và (SAD) (ABCD).
a) Tính theo a thể tích của khối chóp S.ABCD.
b) Tính khoảng cách giữa hai đường thẳng AD và SC.
Bài 7.42 trang 65 Toán 11 Tập 2
Cho hình hộp ABCD.A'B'C'D' có độ dài tất cả các cạnh bằng a, AA' (ABCD) và 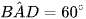= 60o.
a) Tính thể tích của khối hộp ABCD.A'B'C'D'.
b) Tính khoảng cách từ A đến mặt phẳng (A'BD).
Bài 7.43 trang 65 Toán 11 Tập 2
Cho hình lăng trụ ABCD.A'B'C'D'. Biết A'.ABCD là hình chóp đều có tất cả các cạnh đều bằng nhau và bằng a. Tính theo a thể tích của khối lăng trụ ABCD.A'B'C'D' và thể tích của khối chóp A'.BB'C'C.
Bài 7.44 trang 65 Toán 11 Tập 2
Cho hình chóp S.ABCD có đáy ABCD là hình thang cân, AB // CD và AB = BC = DA = a, CD = 2a. Biết hai mặt phẳng (SAC) và (SBD) cùng vuông góc với mặt phẳng đáy (ABCD) và 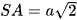SA = . Tính theo a khoảng cách từ S đến mặt phẳng (ABCD) và thể tích của khối chóp S.ABCD.
Bài 7.45 trang 65 Toán 11 Tập 2
Trên mặt đất phẳng, người ta dựng một cây cột AB có chiều dài bằng 10 m và tạo với mặt đất góc 80°. Tại một thời điểm dưới ánh sáng mặt trời, bóng BC của cây cột trên mặt đất dài 12 m vào tạo với cây cột một góc bằng 120° (tức là 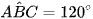= 120o). Tính góc giữa mặt đất và đường thẳng chứa tia sáng mặt trời tại thời điểm nói trên.