Giải bài tập Toán 11 Chương 5: Giới hạn. Hàm số liên tục | Kết Nối Tri Thức
Hướng dẫn giải Chương 5: Giới hạn. Hàm số liên tục
Giải bài tập Bài 15: Giới hạn của dãy số

Bài 5.1 trang 109 Toán 11 Tập 1
Tìm các giới hạn sau. Bài 5.1 trang 109 Toán 11 Tập 1
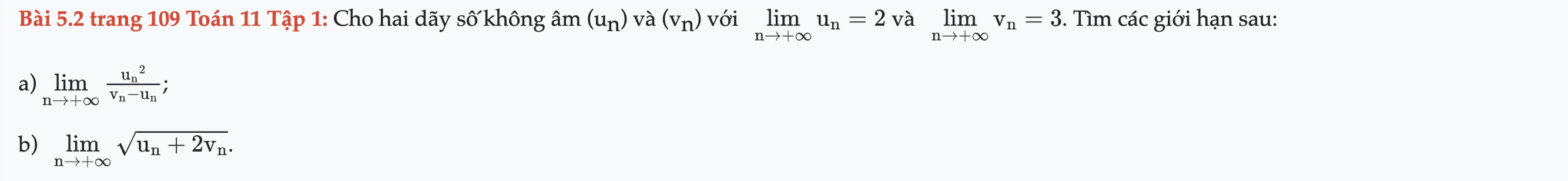
Bài 5.2 trang 109 Toán 11 Tập 1
Cho hai dãy số không âm (un) và (vn). Tìm các giới hạn sau. Bài 5.2 trang 109 Toán 11 Tập 1

Bài 5.3 trang 109 Toán 11 Tập 1
Tìm giới hạn của các dãy số cho bởi. Bài 5.3 trang 109 Toán 11 Tập 1

Bài 5.4 trang 109 Toán 11 Tập 1
Viết các số thập phân vô hạn tuần hoàn sau đây dưới dạng phân số: 1,(12) = 1,121212...; 3,(102) = 3,102102102... Bài 5.4 trang 109 Toán 11 Tập 1
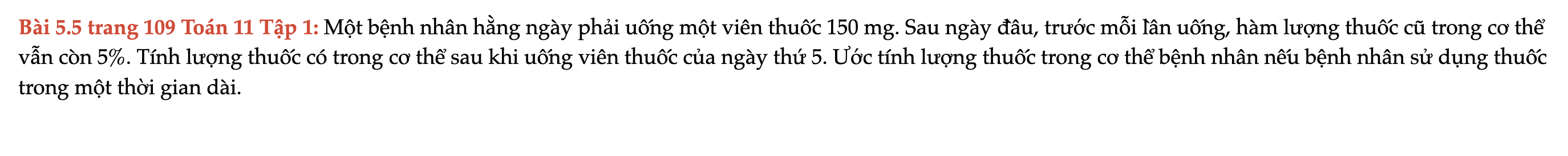
Bài 5.5 trang 109 Toán 11 Tập 1
Một bệnh nhân hằng ngày phải uống một viên thuốc 150 mg. Sau ngày đầu, trước mỗi lần uống, hàm lượng thuốc cũ trong cơ thể vẫn còn 5%. Tính lượng thuốc có trong cơ thể sau khi uống viên thuốc của ngày thứ 5. Bài 5.5 trang 109 Toán 11 Tập 1

Bài 5.6 trang 109 Toán 11 Tập 1
Cho tam giác vuông ABC vuông tại A, có AB = h và góc B bằng α (H.5.3). Từ A kẻ AA1 ⊥ BC, từ A1 kẻ A1A2 ⊥ AC, sau đó lại kẻ A2A3 ⊥ BC. Tiếp tục quá trình trên, ta được đường gấp khúc vô hạn AA1A2A3... Bài 5.6 trang 109 Toán 11 Tập 1

HĐ1 trang 105 Toán 11 Tập 1
Nhận biết dãy số có giới hạn là 0. Cho dãy số (un). Biểu diễn năm số hạng đầu của dãy số này trên trục số. HĐ1 trang 105 Toán 11 Tập 1
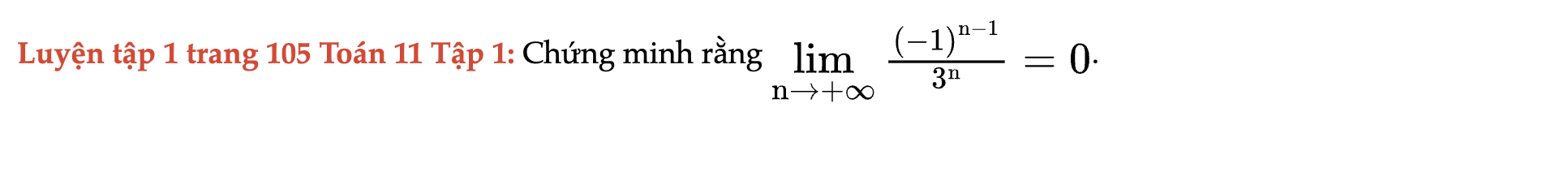
Luyện tập 1 trang 105 Toán 11 Tập 1
Luyện tập 1 trang 105 Toán 11 Tập 1

HĐ2 trang 105 Toán 11 Tập 1
Nhận biết dãy số có giới hạn hữu hạn. HĐ2 trang 105 Toán 11 Tập 1
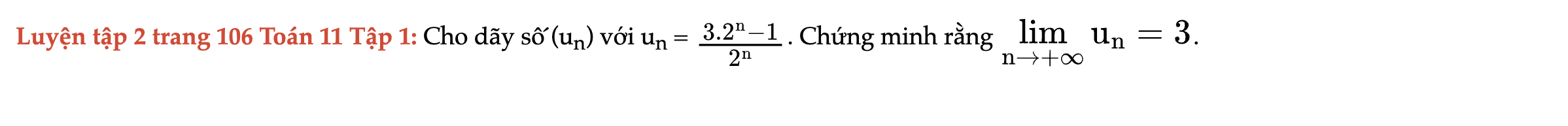
Luyện tập 2 trang 106 Toán 11 Tập 1
Luyện tập 2 trang 106 Toán 11 Tập 1

Vận dụng 1 trang 106 Toán 11 Tập 1
Một quả bóng cao su được thả từ độ cao 5 m xuống mặt sàn. Sau mỗi lần chạm sàn, quả bóng nảy lên độ cao bằng 2/3 độ cao trước đó. Vận dụng 1 trang 106 Toán 11 Tập 1

HĐ3 trang 106 Toán 11 Tập 1
Hình thành quy tắc tính giới hạn. HĐ3 trang 106 Toán 11 Tập 1
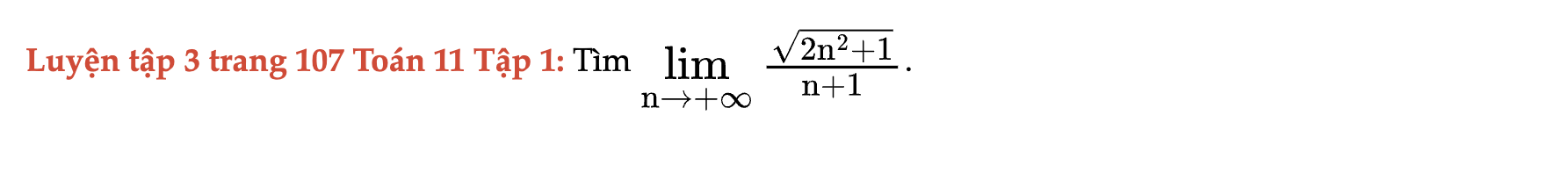
Luyện tập 3 trang 107 Toán 11 Tập 1
Tìm giới hạn sau. Luyện tập 3 trang 107 Toán 11 Tập 1

HĐ4 trang 107 Toán 11 Tập 1
Làm quen với việc tính tổng vô hạn. Cho hình vuông cạnh 1 (đơn vị độ dài). Chia hình vuông đó thành bốn hình vuông nhỏ bằng nhau, sau đó tô màu hình vuông nhỏ góc dưới bên trái (H.5.2). HĐ4 trang 107 Toán 11 Tập 1
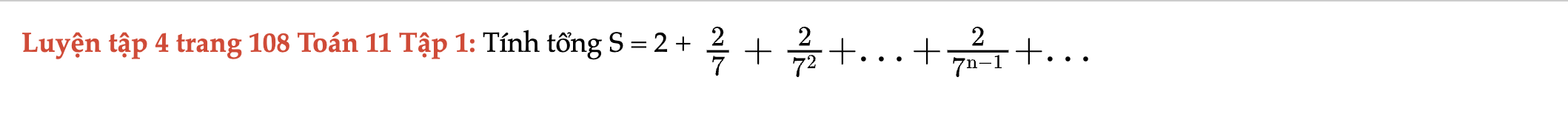
Luyện tập 4 trang 108 Toán 11 Tập 1
Luyện tập 4 trang 108 Toán 11 Tập 1

Vận dụng 2 trang 108 Toán 11 Tập 1
(Giải thích nghịch lí Zeno). Để đơn giản, ta giả sử Achilles chạy với vận tốc 100 km/h, vận tốc của rùa là 1 km/h và khoảng cách ban đầu là a = 100 (km). Vận dụng 2 trang 108 Toán 11 Tập 1

HĐ5 trang 108 Toán 11 Tập 1
Nhận biết giới hạn vô cực. Một loại vi khuẩn được nuôi cấy với số lượng ban đầu là 50. Sau mỗi chu kì 4 giờ, số lượng của chúng sẽ tăng gấp đôi. HĐ5 trang 108 Toán 11 Tập 1
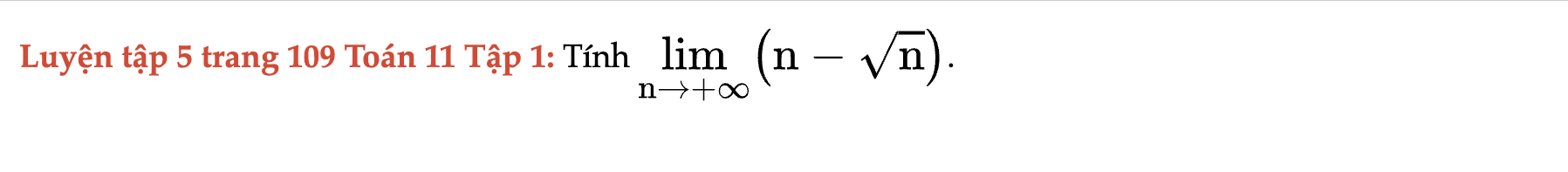
Luyện tập 5 trang 109 Toán 11 Tập 1
Tính giới hạn sau. Luyện tập 5 trang 109 Toán 11 Tập 1
Giải bài tập Bài 16: Giới hạn của hàm số

Bài 5.7 trang 118 Toán 11 Tập 1
Khẳng định nào sau đây là đúng. Bài 5.7 trang 118 Toán 11 Tập 1

Bài 5.8 trang 118 Toán 11 Tập 1
Tính các giới hạn sau. Bài 5.8 trang 118 Toán 11 Tập 1

Bài 5.9 trang 118 Toán 11 Tập 1
Cho hàm số H(t) (hàm Heaviside, thường được dùng để mô tả việc chuyển trạng thái tắt/mở của dòng điện tại thời điểm t = 0). Bài 5.9 trang 118 Toán 11 Tập 1

Bài 5.10 trang 118 Toán 11 Tập 1
Tính các giới hạn một bên. Bài 5.10 trang 118 Toán 11 Tập 1
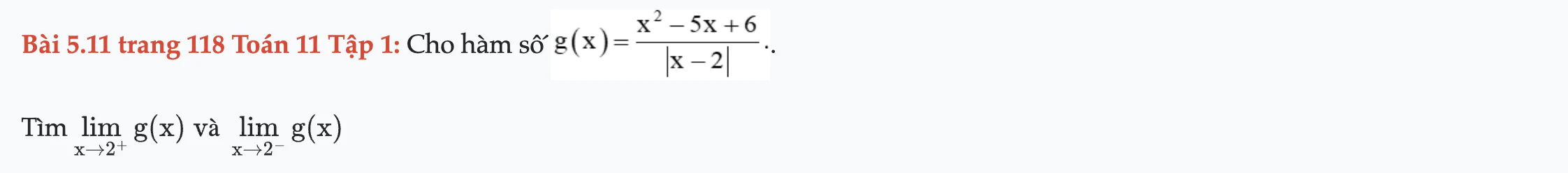
Bài 5.11 trang 118 Toán 11 Tập 1
Bài 5.11 trang 118 Toán 11 Tập 1

Bài 5.12 trang 118 Toán 11 Tập 1
Tính các giới hạn sau. Bài 5.12 trang 118 Toán 11 Tập 1
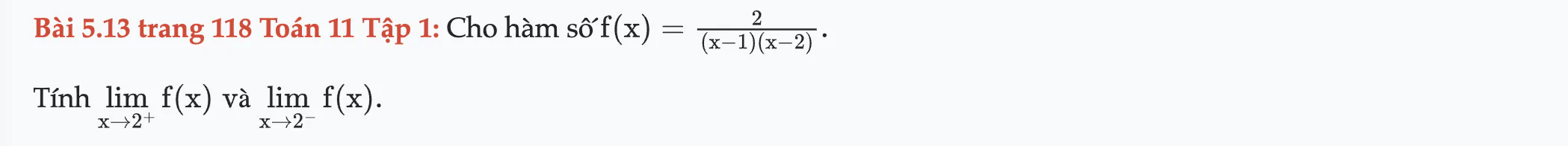
Bài 5.13 trang 118 Toán 11 Tập 1
Bài 5.13 trang 118 Toán 11 Tập 1

Mở đầu trang 111 Toán 11 Tập 1
Trong Thuyết tương đối của Einstein, khối lượng của vật chuyển động với vận tốc v cho bởi công thức m, trong đó m0 là khối lượng của vật khi nó đứng yên, c là vận tốc ánh sáng. Mở đầu trang 111 Toán 11 Tập 1

HĐ1 trang 111 Toán 11 Tập 1
Nhận biết khái niệm giới hạn tại một điểm. Cho hàm số f(x). Tìm tập xác định của hàm số f(x). HĐ1 trang 111 Toán 11 Tập 1
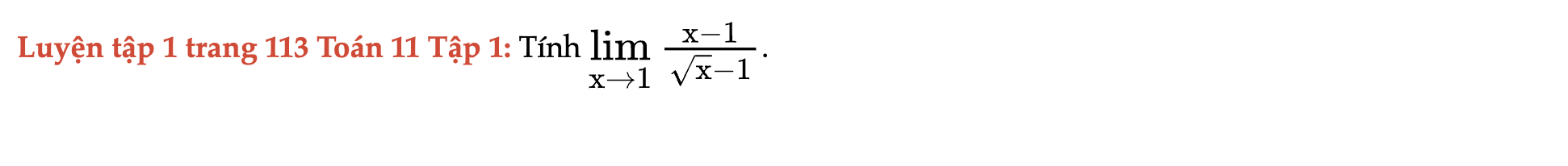
Luyện tập 1 trang 113 Toán 11 Tập 1
Luyện tập 1 trang 113 Toán 11 Tập 1
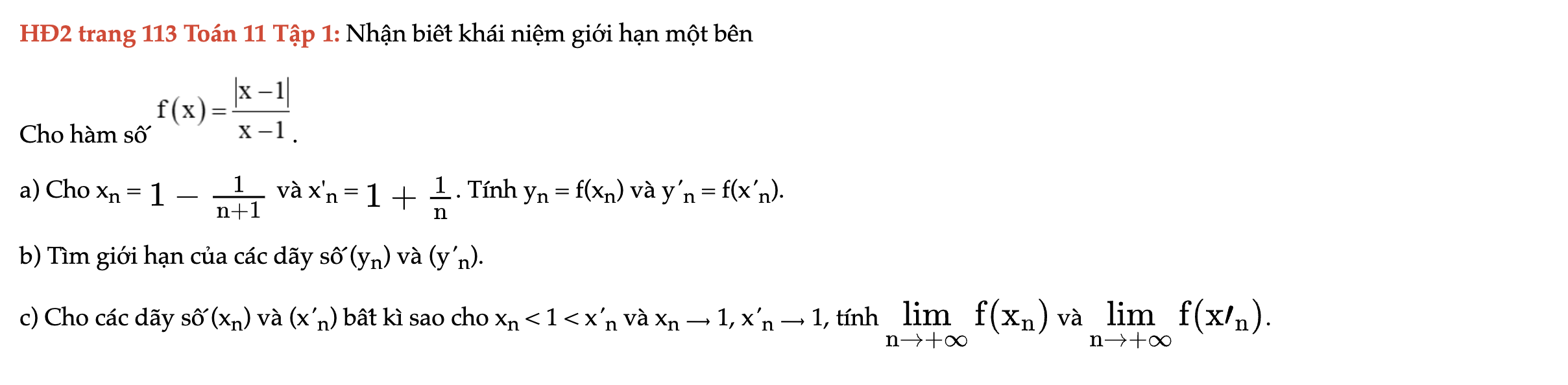
HĐ2 trang 113 Toán 11 Tập 1
Nhận biết khái niệm giới hạn một bên. HĐ2 trang 113 Toán 11 Tập 1

Luyện tập 2 trang 113 Toán 11 Tập 1
Cho hàm số f(x). Tính các giớ hạn tới một điểm sau đây. Luyện tập 2 trang 113 Toán 11 Tập 1

HĐ3 trang 114 Toán 11 Tập 1
Nhận biết khái niệm giới hạn tại vô cực. Cho hàm số f(x) có đồ thị như Hình 5.4. Tính f(xn) và tìm giới hạn sau. HĐ3 trang 114 Toán 11 Tập 1
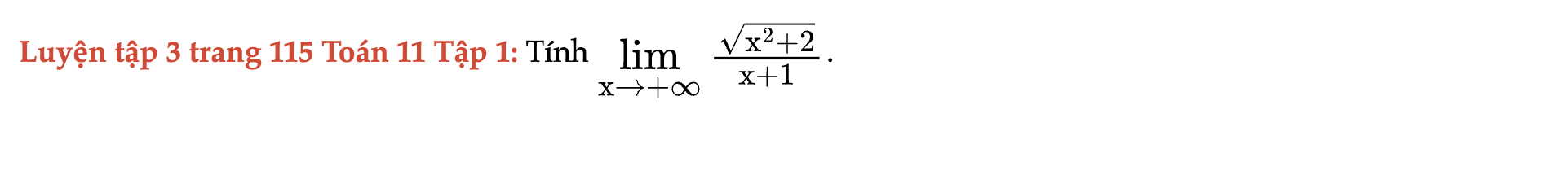
Luyện tập 3 trang 115 Toán 11 Tập 1
Tính giới hạn sau. Luyện tập 3 trang 115 Toán 11 Tập 1

Vận dụng trang 115 Toán 11 Tập 1
Cho tam giác vuông OAB với A = (a; 0) và B = (0; 1) như Hình 5.5. Đường cao OH có độ dài là h. Tính h theo a. Khi điểm A dịch chuyển về O, điểm H thay đổi thế nào? Tại sao? Vận dụng trang 115 Toán 11 Tập 1

HĐ4 trang 115 Toán 11 Tập 1
Nhận biết khái niệm giới hạn vô cực. Xét hàm số f(x) có đồ thị như Hình 5.6. HĐ4 trang 115 Toán 11 Tập 1
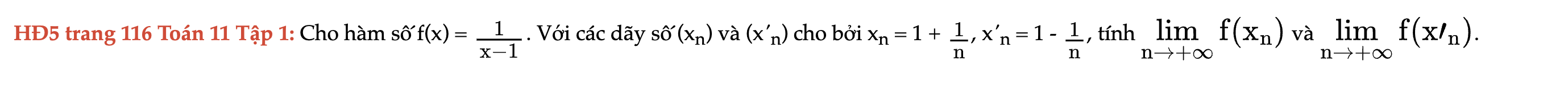
HĐ5 trang 116 Toán 11 Tập 1
HĐ5 trang 116 Toán 11 Tập 1

Luyện tập 4 trang 116 Toán 11 Tập 1
Tính các giới hạn sau. Luyện tập 4 trang 116 Toán 11 Tập 1
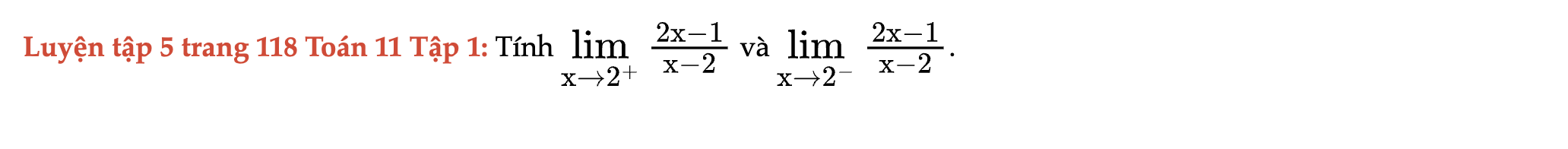
Luyện tập 5 trang 118 Toán 11 Tập 1
Tính các giới hạn sau. Luyện tập 5 trang 118 Toán 11 Tập 1
Giải bài tập Bài 17: Hàm số liên tục
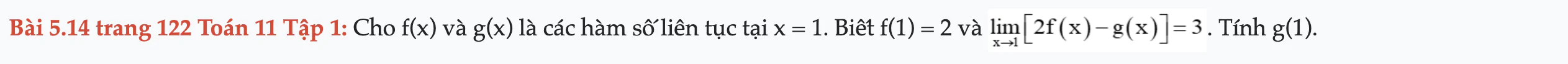
Bài 5.14 trang 122 Toán 11 Tập 1
Bài 5.14 trang 122 Toán 11 Tập 1

Bài 5.15 trang 122 Toán 11 Tập 1
Xét tính liên tục của các hàm số sau trên tập xác định của chúng. Bài 5.15 trang 122 Toán 11 Tập 1
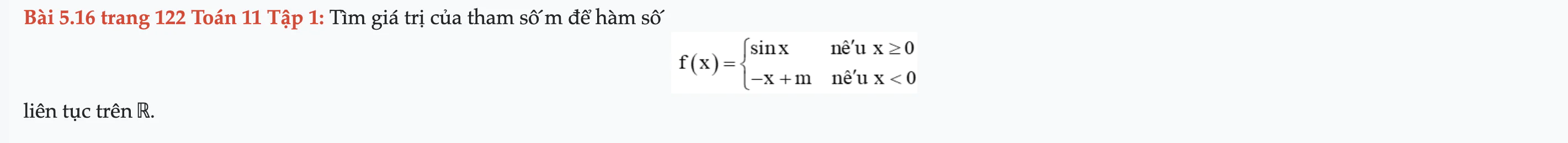
Bài 5.16 trang 122 Toán 11 Tập 1
Tìm giá trị của tham số m để hàm số liên tục trên ℝ. Bài 5.16 trang 122 Toán 11 Tập 1

Bài 5.17 trang 122 Toán 11 Tập 1
Một bảng giá cước taxi được cho như sau. Viết công thức hàm số mô tả số tiền khách phải trả theo quãng đường di chuyển. Bài 5.17 trang 122 Toán 11 Tập 1

Mở đầu trang 119 Toán 11 Tập 1
Một người lái xe từ địa điểm A đến địa điểm B trong thời gian 3 giờ. Biết quãng đường từ A đến B dài 180 km. Chứng tỏ rằng có ít nhất một thời điểm trên hành trình, xe chạy với vận tốc 60 km/h. Mở đầu trang 119 Toán 11 Tập 1

HĐ1 trang 119 Toán 11 Tập 1
Nhận biết tính liên tục của hàm số tại một điểm. Cho hàm số f(x). HĐ1 trang 119 Toán 11 Tập 1
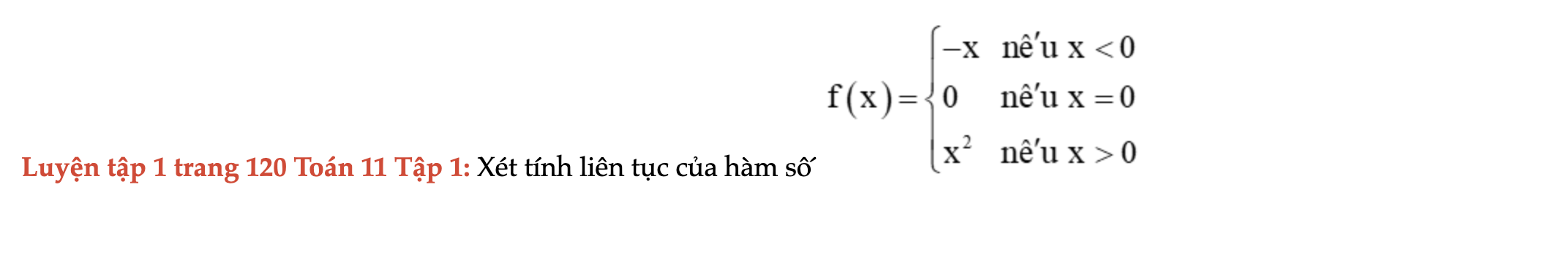
Luyện tập 1 trang 120 Toán 11 Tập 1
Xét tính liên tục của hàm số . Luyện tập 1 trang 120 Toán 11 Tập 1

HĐ2 trang 120 Toán 11 Tập 1
Cho hai hàm số f(x) và g(x) với đồ thị tương ứng như Hình 5.7. Xét tính liên tục của các hàm số f(x) và g(x) tại điểm x = 1/2 và nhận xét về sự khác nhau giữa hai đồ thị. HĐ2 trang 120 Toán 11 Tập 1
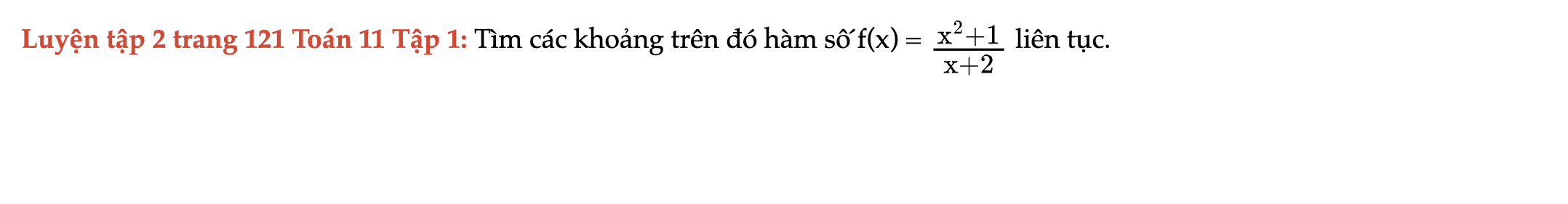
Luyện tập 2 trang 121 Toán 11 Tập 1
Tìm các khoảng trên đó hàm số f(x) liên tục. Luyện tập 2 trang 121 Toán 11 Tập 1
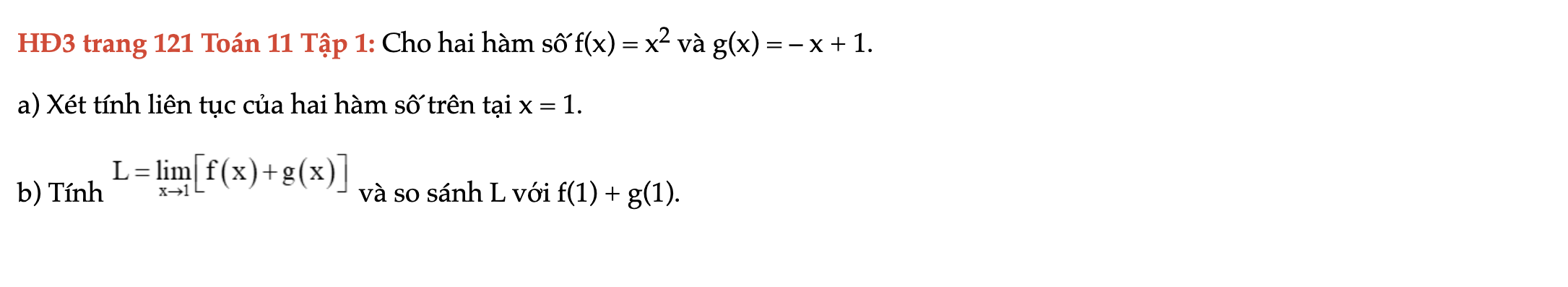
HĐ3 trang 121 Toán 11 Tập 1
Cho hai hàm số f(x) và g(x). Xét tính liên tục của hai hàm số trên tại x = 1. HĐ3 trang 121 Toán 11 Tập 1

Vận dụng trang 122 Toán 11 Tập 1
Giải bài toán ở tình huống mở đầu. Vận dụng trang 122 Toán 11 Tập 1
Giải bài tập Bài tập cuối chương 5
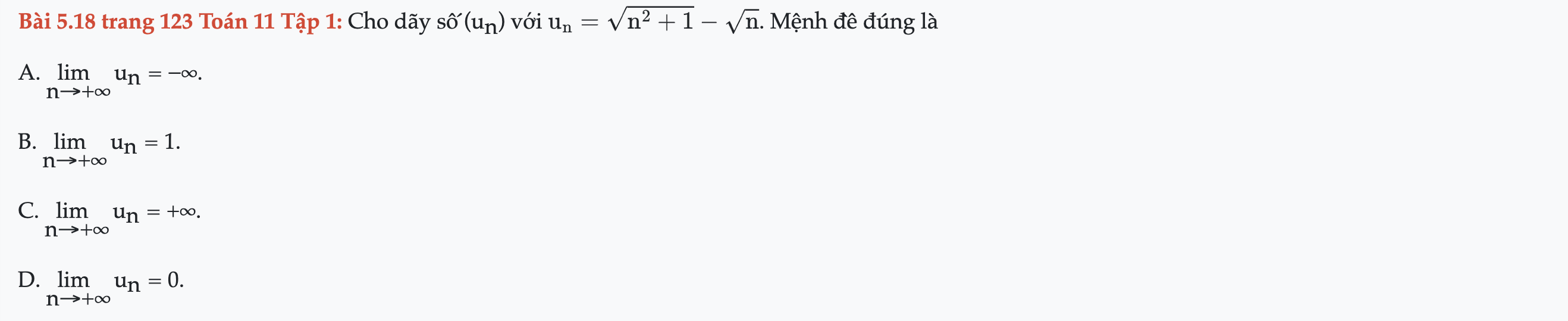
Bài 5.18 trang 123 Toán 11 Tập 1
Cho dãy số (un). Mệnh đề đúng là. Bài 5.18 trang 123 Toán 11 Tập 1
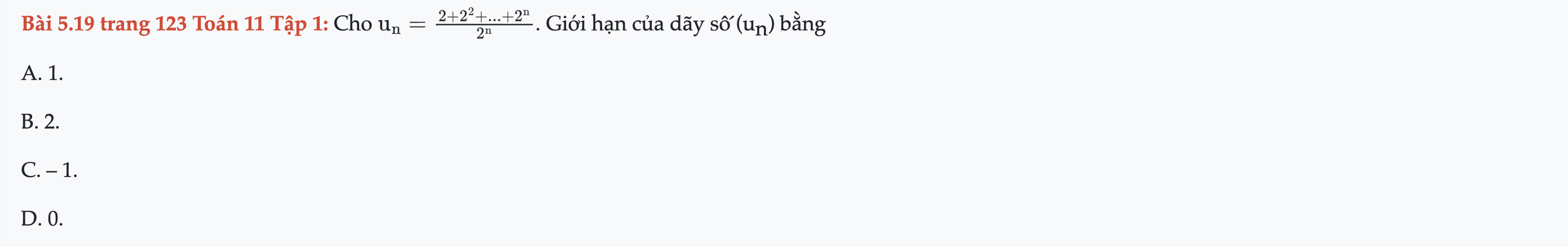
Bài 5.19 trang 123 Toán 11 Tập 1
Cho un, tìm giới hạn của dãy số (un). Bài 5.19 trang 123 Toán 11 Tập 1
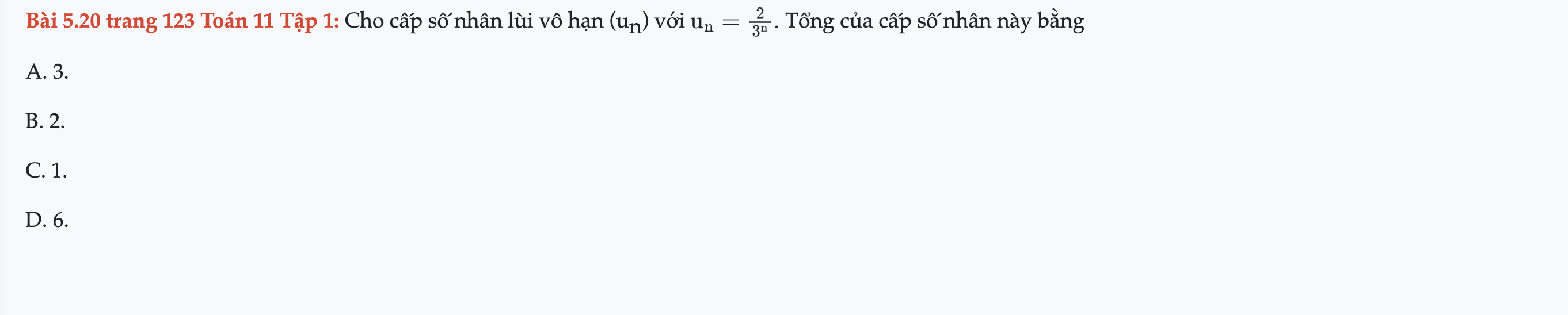
Bài 5.20 trang 123 Toán 11 Tập 1
Cho cấp số nhân lùi vô hạn (un). Tổng của cấp số nhân này bằng. Bài 5.20 trang 123 Toán 11 Tập 1

Bài 5.21 trang 123 Toán 11 Tập 1
Cho hàm số f(x). Tìm mệnh đề đúng. Bài 5.21 trang 123 Toán 11 Tập 1
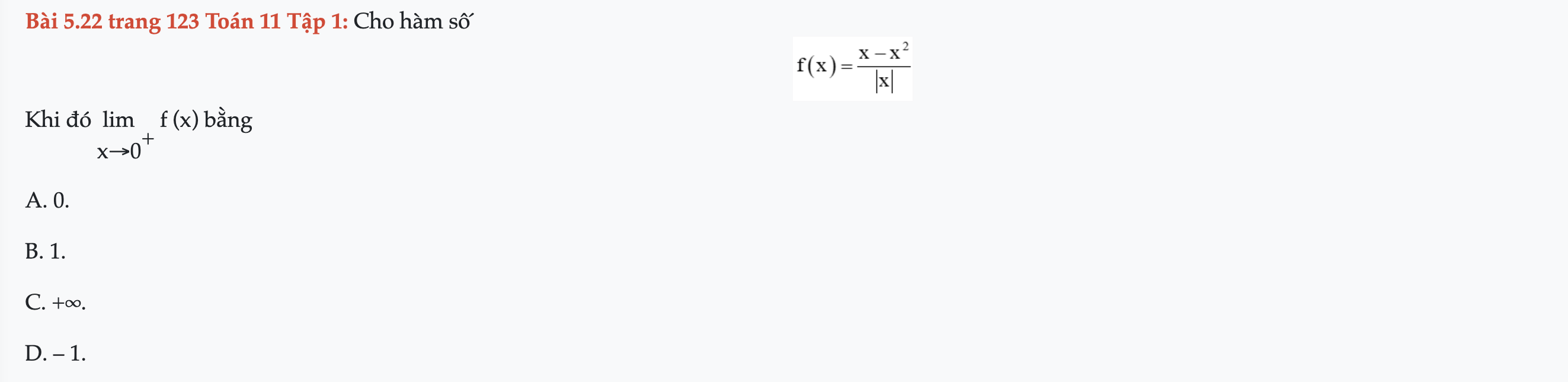
Bài 5.22 trang 123 Toán 11 Tập 1
Cho hàm số f(x). Khi đó tìm giới hạn khi x→0+. Bài 5.22 trang 123 Toán 11 Tập 1

Bài 5.23 trang 123 Toán 11 Tập 1
Cho hàm số f(x). Hàm số f(x) liên tục trên. Bài 5.23 trang 123 Toán 11 Tập 1

Bài 5.24 trang 123 Toán 11 Tập 1
Cho hàm số f(x) liên tục tại x = 1 khi a bằng bao nhiêu. Bài 5.24 trang 123 Toán 11 Tập 1
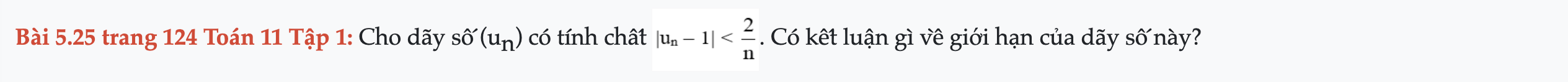
Bài 5.25 trang 124 Toán 11 Tập 1
Cho dãy số (un). Có kết luận gì về giới hạn của dãy số này. Bài 5.25 trang 124 Toán 11 Tập 1

Bài 5.26 trang 124 Toán 11 Tập 1
Tìm giới hạn của các dãy số có số hạng tổng quát cho bởi công thức sau. Bài 5.26 trang 124 Toán 11 Tập 1

Bài 5.27 trang 124 Toán 11 Tập 1
Viết các số thập phân vô hạn tuần hoàn sau đây dưới dạng phân số. Bài 5.27 trang 124 Toán 11 Tập 1

Bài 5.28 trang 124 Toán 11 Tập 1
Tính các giới hạn sau. Bài 5.28 trang 124 Toán 11 Tập 1

Bài 5.29 trang 124 Toán 11 Tập 1
Tính các giới hạn một bên. Bài 5.29 trang 124 Toán 11 Tập 1
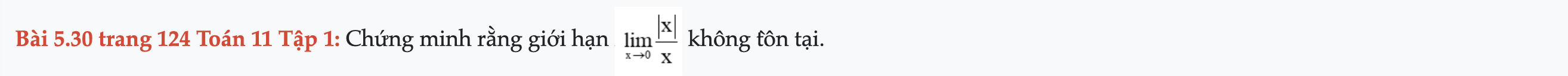
Bài 5.30 trang 124 Toán 11 Tập 1
Chứng minh rằng giới hạn sau không tồn tại. Bài 5.30 trang 124 Toán 11 Tập 1

Bài 5.31 trang 124 Toán 11 Tập 1
Giải thích tại sao các hàm số sau đây gián đoạn tại điểm đã cho. Bài 5.31 trang 124 Toán 11 Tập 1

Bài 5.32 trang 124 Toán 11 Tập 1
Lực hấp dẫn tác dụng lên một đơn vị khối lượng ở khoảng cách r tính từ tâm Trái Đất là. Bài 5.32 trang 124 Toán 11 Tập 1

Bài 5.33 trang 124 Toán 11 Tập 1
Tìm tập xác định của các hàm số sau và giải thích tại sao các hàm này liên tục trên các khoảng xác định của chúng. Bài 5.33 trang 124 Toán 11 Tập 1
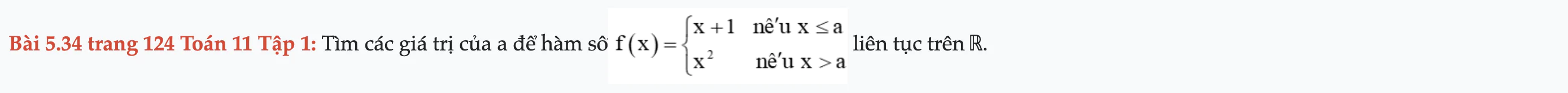
Bài 5.34 trang 124 Toán 11 Tập 1
Tìm các giá trị của a để hàm số liên tục trên ℝ. Bài 5.34 trang 124 Toán 11 Tập 1