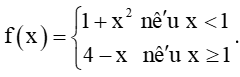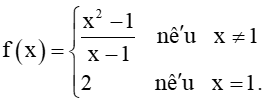Giải bài tập Luyện tập 1 trang 120 Toán 11 Tập 1 | Toán 11 - Kết nối tri thức
Hướng dẫn giải chi tiết từng bước bài tập Luyện tập 1 trang 120 Toán 11 Tập 1. Bài 17: Hàm số liên tục. Toán 11 - Kết nối tri thức
Đề bài:
Xét tính liên tục của hàm số 
Đáp án và cách giải chi tiết:
Hàm số f(x) xác định trên ℝ, do đó x0 = 0 thuộc tập xác định của hàm số.
Ta có: .
Do đó, , suy ra .
Lại có f(0) = 0 nên = f(0). Vậy hàm số f(x) liên tục tại x0 = 0.
Nguồn: loigiaitoan.com
Tổng số đánh giá:
Xếp hạng: / 5 sao
Bài tập liên quan:
Bài 5.14 trang 122 Toán 11 Tập 1
Cho f(x) và g(x) là các hàm số liên tục tại x = 1. Biết f(1) = 2 và . Tính g(1).
Bài 5.15 trang 122 Toán 11 Tập 1
Xét tính liên tục của các hàm số sau trên tập xác định của chúng:
a) ;
b)
Bài 5.16 trang 122 Toán 11 Tập 1
Tìm giá trị của tham số m để hàm số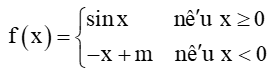
Bài 5.17 trang 122 Toán 11 Tập 1
Một bảng giá cước taxi được cho như sau:

a) Viết công thức hàm số mô tả số tiền khách phải trả theo quãng đường di chuyển.
b) Xét tính liên tục của hàm số ở câu a.
Mở đầu trang 119 Toán 11 Tập 1
Một người lái xe từ địa điểm A đến địa điểm B trong thời gian 3 giờ. Biết quãng đường từ A đến B dài 180 km. Chứng tỏ rằng có ít nhất một thời điểm trên hành trình, xe chạy với vận tốc 60 km/h.

HĐ1 trang 119 Toán 11 Tập 1
Nhận biết tính liên tục của hàm số tại một điểm
Cho hàm số
Tìm giới hạn và so sánh giá trị này với f(1).
HĐ2 trang 120 Toán 11 Tập 1
Cho hai hàm số  với đồ thị tương ứng như Hình 5.7.
với đồ thị tương ứng như Hình 5.7.
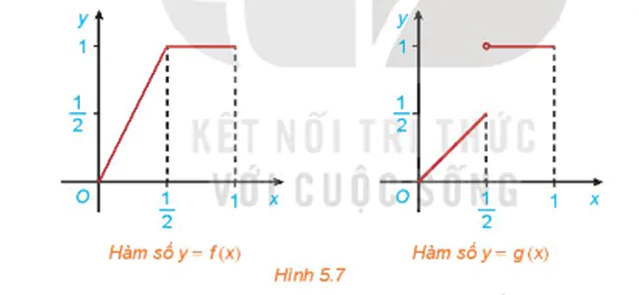
Xét tính liên tục của các hàm số f(x) và g(x) tại điểm x = và nhận xét về sự khác nhau giữa hai đồ thị.
Luyện tập 2 trang 121 Toán 11 Tập 1
Tìm các khoảng trên đó hàm số f(x) = liên tục.
HĐ3 trang 121 Toán 11 Tập 1
Cho hai hàm số f(x) = x2 và g(x) = – x + 1.
a) Xét tính liên tục của hai hàm số trên tại x = 1.
b) Tính và so sánh L với f(1) + g(1).