Giải bài tập Toán 12 Chương 5. Phương pháp tọa độ trong không gian | Kết Nối Tri Thức
Hướng dẫn giải Chương 5. Phương pháp tọa độ trong không gian. Tìm hiểu về Phương trình mặt phẳng, đường thẳng, mặt cầu trong không gian Oxyz và cách vận dụng để giải quyết vấn đề trong thực tiễn.
Giải bài tập Bài 14. Phương trình mặt phẳng.

Bài 5.1 trang 39 Toán 12 Tập 2
Trong không gian Oxyz, viết phương trình mặt phẳng đi qua điểm M(1; 2; −1) và vuông góc với trục Ox. Bài 5.1 trang 39 Toán 12 Tập 2

Bài 5.2 trang 39 Toán 12 Tập 2
Trong không gian Oxyz, cho hình hộp ABCD.A'B'C'D', với A(1; −1; 3), B(0; 2; 4), D(2; −1; 1), A'(0; 1; 2). Bài 5.2 trang 39 Toán 12 Tập 2

Bài 5.3 trang 39 Toán 12 Tập 2
Trong không gian Oxyz, viết phương trình mặt phẳng (P) đi qua điểm M(1; −1; 5) và vuông góc với hai mặt phẳng (Q): 3x + 2y – z = 0, (R): x + y – z = 0. Bài 5.3 trang 39 Toán 12 Tập 2

Bài 5.4 trang 39 Toán 12 Tập 2
Trong không gian Oxyz, viết phương trình mặt phẳng đi qua M(2; 3; −1), song song với trục Ox và vuông góc với mặt phẳng (Q): x + 2y – 3z + 1 = 0. Bài 5.4 trang 39 Toán 12 Tập 2
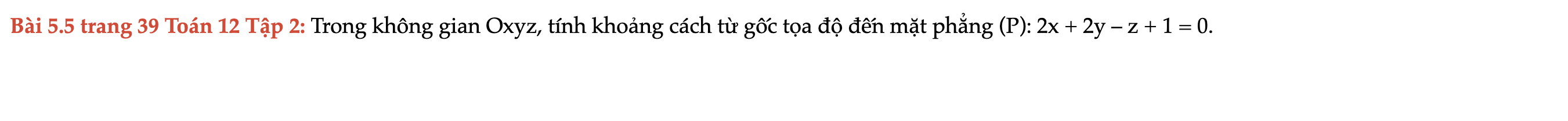
Bài 5.5 trang 39 Toán 12 Tập 2
Trong không gian Oxyz, tính khoảng cách từ gốc tọa độ đến mặt phẳng (P): 2x + 2y – z + 1 = 0. Bài 5.5 trang 39 Toán 12 Tập 2
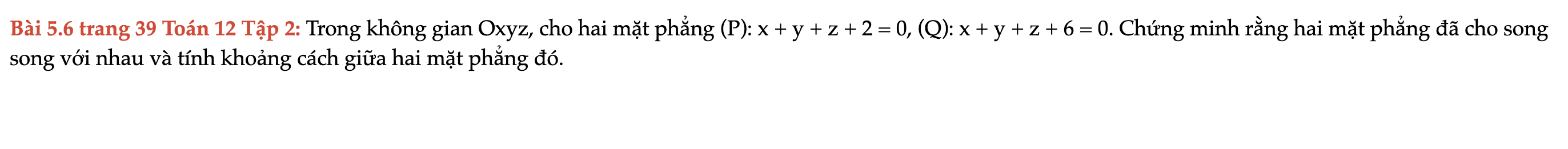
Bài 5.6 trang 39 Toán 12 Tập 2
Trong không gian Oxyz, cho hai mặt phẳng (P): x + y + z + 2 = 0, (Q): x + y + z + 6 = 0. Chứng minh rằng hai mặt phẳng đã cho song song với nhau và tính khoảng cách giữa hai mặt phẳng đó. Bài 5.6 trang 39 Toán 12 Tập 2
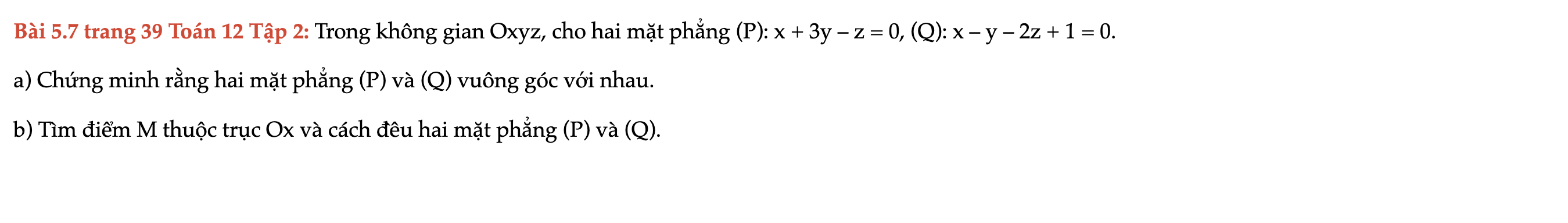
Bài 5.7 trang 39 Toán 12 Tập 2
Trong không gian Oxyz, cho hai mặt phẳng (P): x + 3y – z = 0, (Q): x – y – 2z + 1 = 0. Bài 5.7 trang 39 Toán 12 Tập 2

Bài 5.8 trang 39 Toán 12 Tập 2
Bác An dự định làm bốn mái của ngôi nhà sao cho chúng là bốn mặt bên của một hình chóp đều và các mái nhà kề nhau thì vuông góc với nhau. Hỏi ý tưởng trên có thực hiện được không. Bài 5.8 trang 39 Toán 12 Tập 2

Bài 5.9 trang 39 Toán 12 Tập 2
Trong không gian Oxyz, một ngôi nhà có sàn nhà thuộc mặt phẳng Oxy, trần nhà tầng 1 thuộc mặt phẳng z – 1 = 0, mái nhà tầng 2 thuộc mặt phẳng x + y + 50z – 100 = 0. Bài 5.9 trang 39 Toán 12 Tập 2

Bài 5.10 trang 40 Toán 12 Tập 2
Xét một cối xay lúa trong không gian Oxyz, với đơn vị đo là mét. Nếu tác động vào tai cối xay lúa (ở vị trí P) một lực F thì moment lực M được tính bởi công thức M=[OP, F]. Bài 5.10 trang 40 Toán 12 Tập 2

Mở đầu trang 29 Toán 12 Tập 2
Một vật thể chuyển động trong không gian Oxyz. Tại mỗi thời điểm t, vật thể ở vị trí M(cost – sint; cost + sint; cost). Hỏi vật thể có chuyển động trong một mặt phẳng cố định hay không? Mở đầu trang 29 Toán 12 Tập 2

HĐ1 trang 29 Toán 12 Tập 2
HĐ1 trang 29 Toán 12 Tập 2
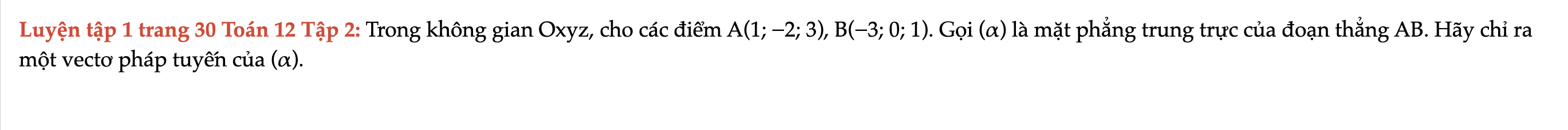
Luyện tập 1 trang 30 Toán 12 Tập 2
Trong không gian Oxyz, cho các điểm A(1; −2; 3), B(−3; 0; 1). Gọi (α) là mặt phẳng trung trực của đoạn thẳng AB. Hãy chỉ ra một vectơ pháp tuyến của (α). Luyện tập 1 trang 30 Toán 12 Tập 2

HĐ2 trang 30 Toán 12 Tập 2
Trong không gian Oxyz, cho hai vectơ u = (a; b; c) và v = (a'; b'; c'). Vectơ n = (bc' - b'c; ca' - c'a; ab' - a'b) có vuông góc với cả hai vectơ u và v hay không? HĐ2 trang 30 Toán 12 Tập 2
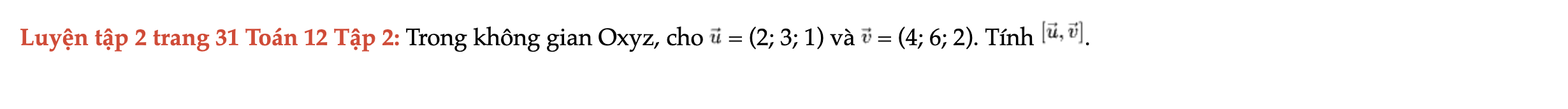
Luyện tập 2 trang 31 Toán 12 Tập 2
Trong không gian Oxyz, cho u = (2; 3; 1) và v = (4; 6; 2). Tính [u, v]. Luyện tập 2 trang 31 Toán 12 Tập 2

HĐ3 trang 31 Toán 12 Tập 2
Trong không gian Oxyz, cho hai vectơ u, v không cùng phương và có giá nằm trong hoặc song song với mặt phẳng (P). Vectơ [u, v] có khác vectơ-không và giá của nó có vuông góc với cả hai giá của vectơ u, v không? HĐ3 trang 31 Toán 12 Tập 2
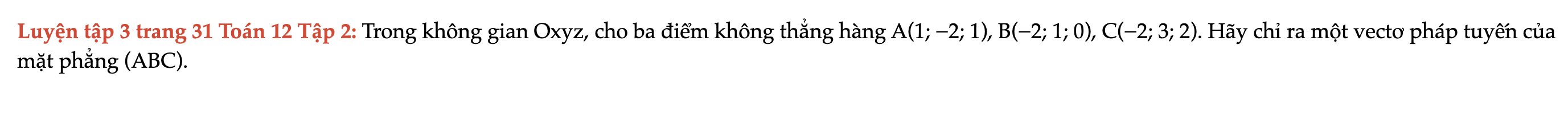
Luyện tập 3 trang 31 Toán 12 Tập 2
Trong không gian Oxyz, cho ba điểm không thẳng hàng A(1; −2; 1), B(−2; 1; 0), C(−2; 3; 2). Hãy chỉ ra một vectơ pháp tuyến của mặt phẳng (ABC). Luyện tập 3 trang 31 Toán 12 Tập 2

Vận dụng 1 trang 31 Toán 12 Tập 2
Moment lực là một đại lượng Vật lí, thể hiện tác động gây ra sự quay quanh một điểm hoặc một trục của một vật thể. Trong không gian Oxyz, với đơn vị đo là mét. Vận dụng 1 trang 31 Toán 12 Tập 2

HĐ4 trang 32 Toán 12 Tập 2
Trong không gian Oxyz, cho mặt phẳng (α). Gọi n = (A; B; C) là một vectơ pháp tuyến của (α) và M0(x0; y0; z0) là một điểm thuộc (α). HĐ4 trang 32 Toán 12 Tập 2

Luyện tập 4 trang 32 Toán 12 Tập 2
Trong không gian Oxyz, phương trình nào trong các phương trình sau là phương trình tổng quát của một mặt phẳng? Luyện tập 4 trang 32 Toán 12 Tập 2
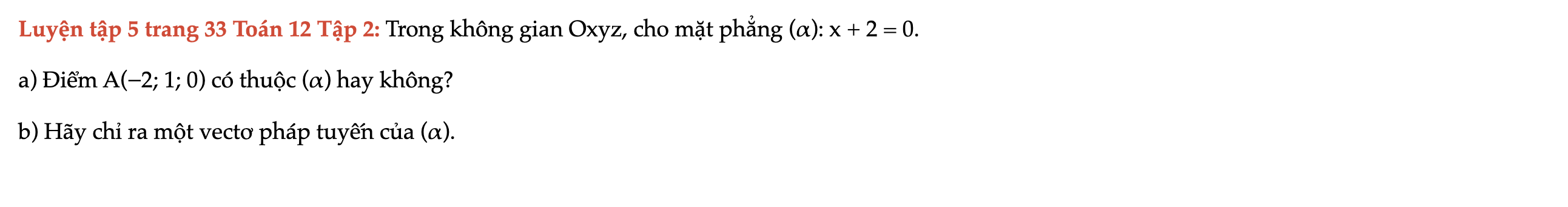
Luyện tập 5 trang 33 Toán 12 Tập 2
Trong không gian Oxyz, cho mặt phẳng (α): x + 2 = 0. Điểm A(−2; 1; 0) có thuộc (α) hay không? Hãy chỉ ra một vectơ pháp tuyến của (α). Luyện tập 5 trang 33 Toán 12 Tập 2

HĐ5 trang 33 Toán 12 Tập 2
Trong không gian Oxyz, cho mặt phẳng (α) đi qua điểm M0(x0; y0; z0) và có vectơ pháp tuyến n = (A; B; C). Dựa vào Hoạt động 4, hãy nêu phương trình của (α). HĐ5 trang 33 Toán 12 Tập 2

Luyện tập 6 trang 33 Toán 12 Tập 2
Trong không gian Oxyz, viết phương trình mặt phẳng (α) đi qua điểm M(1; 2; −4) và vuông góc với trục Oz. Luyện tập 6 trang 33 Toán 12 Tập 2

HĐ6 trang 33 Toán 12 Tập 2
Trong không gian Oxyz, cho mặt phẳng (α) đi qua điểm M(x0; y0; z0) và biết cặp vectơ chỉ phương u = (a; b; c) và v = (a'; b'; c'). Hãy chỉ ra một vectơ pháp tuyến của mặt phẳng (α). Viết phương trình mặt phẳng (α). HĐ6 trang 33 Toán 12 Tập 2
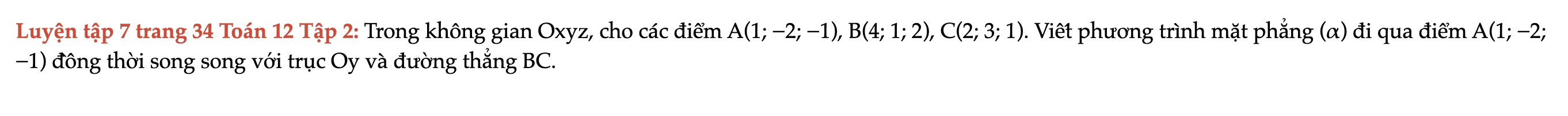
Luyện tập 7 trang 34 Toán 12 Tập 2
Trong không gian Oxyz, cho các điểm A(1; −2; −1), B(4; 1; 2), C(2; 3; 1). Viết phương trình mặt phẳng (α) đi qua điểm A(1; −2; −1) đồng thời song song với trục Oy và đường thẳng BC. Luyện tập 7 trang 34 Toán 12 Tập 2

HĐ7 trang 34 Toán 12 Tập 2
Trong không gian Oxyz, cho ba điểm không thẳng hàng: A(1; 2; 3), B(−1; 3; 4), C(2; −1; 2). Hãy chỉ ra một cặp vectơ chỉ phương của mặt phẳng (ABC). Viết phương trình mặt phẳng (ABC). HĐ7 trang 34 Toán 12 Tập 2

Luyện tập 8 trang 35 Toán 12 Tập 2
H.5.8) Trong không gian Oxyz, cho mặt phẳng (α) không đi qua gốc tọa độ và cắt ba trục Ox, Oy, Oz tương ứng tại các điểm A(a; 0; 0), B(0; b; 0), C(0; 0; c) (a, b, c ≠ 0). Luyện tập 8 trang 35 Toán 12 Tập 2

Vận dụng 2 trang 35 Toán 12 Tập 2
Trong tình huống mở đầu, hãy thực hiện các bước sau và trả lời câu hỏi đã được nêu ra. Xác định tọa độ của vị trí M1, M2, M3 của vật tương ứng với các thời điểm t = 0, t = π/2, t = π. Vận dụng 2 trang 35 Toán 12 Tập 2

HĐ8 trang 35 Toán 12 Tập 2
Trong không gian Oxyz, cho hai mặt phẳng: (α): Ax + By + Cz + D = 0, (β): A'x + B'y + C'z + D' = 0, với hai vectơ pháp tuyến n = (A; B; C), n' = (A'; B'; C') tương ứng. HĐ8 trang 35 Toán 12 Tập 2

Luyện tập 9 trang 36 Toán 12 Tập 2
Trong không gian Oxyz, hai mặt phẳng sau đây có vuông góc với nhau hay không? (α): 3x + y – z + 1 = 0, (β): 9x + 3y – 3z + 3 = 0. Luyện tập 9 trang 36 Toán 12 Tập 2

Vận dụng 3 trang 36 Toán 12 Tập 2
(H.5.10) Trong không gian Oxyz, sàn của một căn phòng có dạng hình tứ giác với bốn đỉnh O(0; 0; 0), A(2; 0; 0), B(2; 3; 0), C(0; căn 2; 0). Bốn bức tường của căn phòng đều vuông góc với sàn. Vận dụng 3 trang 36 Toán 12 Tập 2

HĐ9 trang 37 Toán 12 Tập 2
Trong không gian Oxyz, cho hai mặt phẳng (α): Ax + By + Cz + D = 0, (β): A'x + B'y + C'x + D' = 0, với các vectơ pháp tuyến n = (A; B; C), n' = (A'; B'; C'). HĐ9 trang 37 Toán 12 Tập 2

Luyện tập 10 trang 37 Toán 12 Tập 2
Trong không gian Oxyz, cho hai mặt phẳng: (α): 5x + 2y – 4z + 6 = 0 và (β): 10x + 4y – 2z + 12 = 0. Hỏi (α) và (β) có song song với nhau hay không? Luyện tập 10 trang 37 Toán 12 Tập 2

Vận dụng 4 trang 37 Toán 12 Tập 2
Trong một kì thi tuyển sinh có ba môn thi Toán, Văn, Tiếng Anh. Trong không gian Oxyz, người ta biểu diễn kết quả thi của mỗi thí sinh bởi điểm có hoành độ, tung độ, cao độ tương ứng là điểm Toán, Văn, Tiếng Anh. Vận dụng 4 trang 37 Toán 12 Tập 2

HĐ10 trang 38 Toán 12 Tập 2
Trong không gian Oxyz, cho điểm M(x0; y0; z0) và mặt phẳng (P): Ax + By + Cz + D = 0 có vectơ pháp tuyến n = (A; B; C). Gọi N là hình chiếu vuông góc của M trên (P) (H.5.13). HĐ10 trang 38 Toán 12 Tập 2

Luyện tập 11 trang 39 Toán 12 Tập 2
Trong không gian Oxyz, cho hai mặt phẳng (P): x + 3y + z + 2 = 0 và (Q): x + 3y + z + 5 = 0. Chứng minh rằng (P) và (Q) song song với nhau. Luyện tập 11 trang 39 Toán 12 Tập 2

Vận dụng 5 trang 39 Toán 12 Tập 2
(H.5.14) Góc quan sát ngang của một camera là 115°. Trong không gian Oxyz, camera được đặt tại điểm C(1; 2; 4) và chiếu thẳng về phía mặt phẳng (P): x + 2y + 2z + 3 = 0. Vận dụng 5 trang 39 Toán 12 Tập 2
Giải bài tập Bài 15. Phương trình đường thẳng trong không gian.
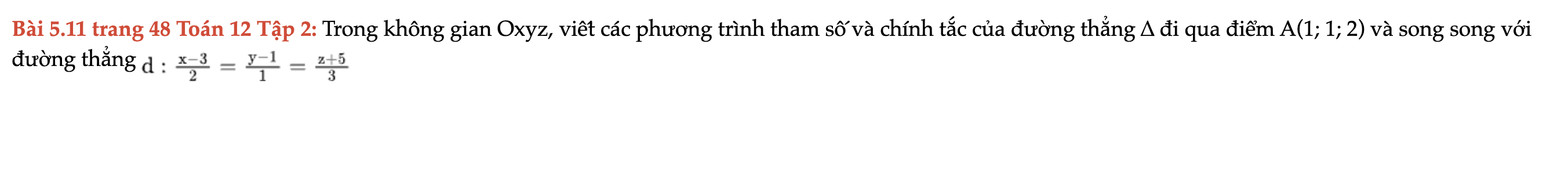
Bài 5.11 trang 48 Toán 12 Tập 2
Trong không gian Oxyz, viết các phương trình tham số và chính tắc của đường thẳng ∆ đi qua điểm A(1; 1; 2) và song song với đường thẳng. Bài 5.11 trang 48 Toán 12 Tập 2
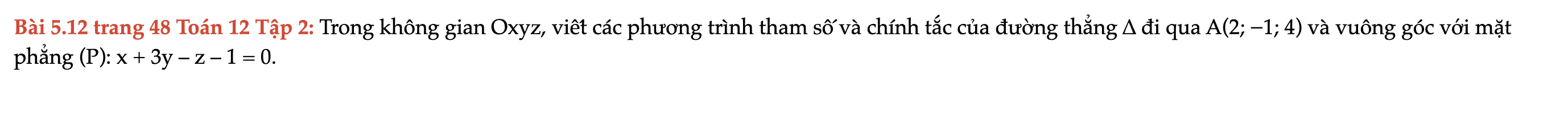
Bài 5.12 trang 48 Toán 12 Tập 2
Trong không gian Oxyz, viết các phương trình tham số và chính tắc của đường thẳng ∆ đi qua A(2; −1; 4) và vuông góc với mặt phẳng (P): x + 3y – z – 1 = 0. Bài 5.12 trang 48 Toán 12 Tập 2
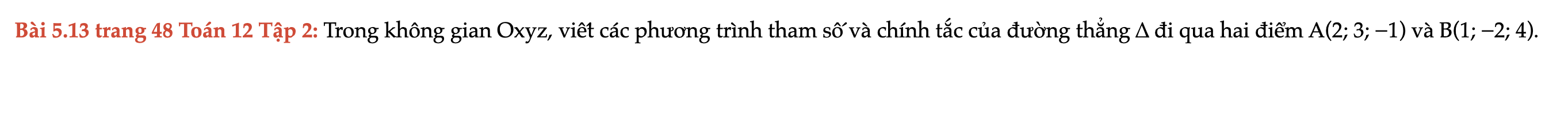
Bài 5.13 trang 48 Toán 12 Tập 2
Trong không gian Oxyz, viết các phương trình tham số và chính tắc của đường thẳng ∆ đi qua hai điểm A(2; 3; −1) và B(1; −2; 4). Bài 5.13 trang 48 Toán 12 Tập 2
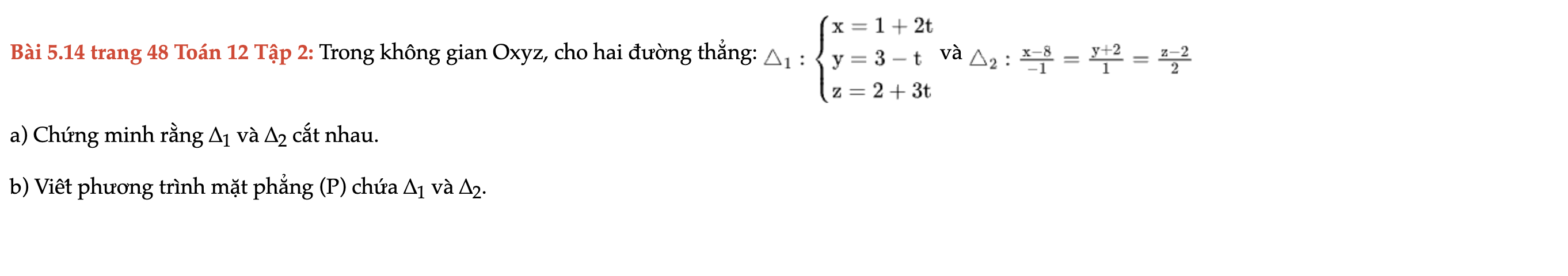
Bài 5.14 trang 48 Toán 12 Tập 2
Trong không gian Oxyz, cho hai đường thẳng chứng minh rằng ∆1 và ∆2 cắt nhau. Bài 5.14 trang 48 Toán 12 Tập 2
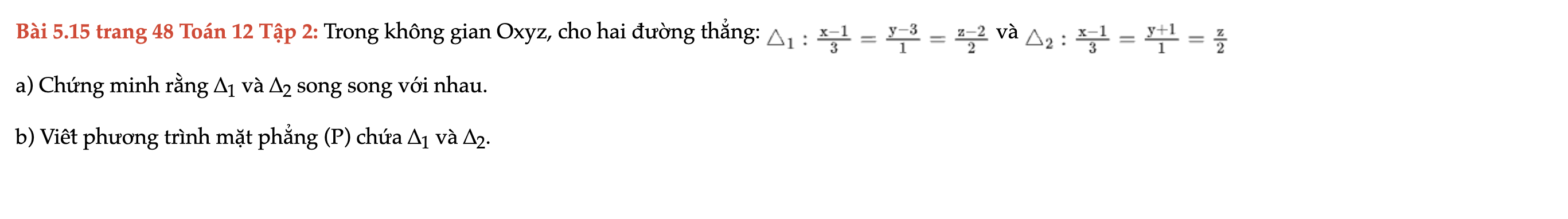
Bài 5.15 trang 48 Toán 12 Tập 2
Bài 5.15 trang 48 Toán 12 Tập 2

Bài 5.16 trang 48 Toán 12 Tập 2
Trong không gian Oxyz, xác định vị trí tương đối giữa hai đường thẳng. Bài 5.16 trang 48 Toán 12 Tập 2

Bài 5.17 trang 49 Toán 12 Tập 2
Tại một nút giao thông có hai con đường. Trên thiết kế, trong không gian Oxyz, hai con đường đó thuộc hai đường thẳng lần lượt có phương trình. Bài 5.17 trang 49 Toán 12 Tập 2

Bài 5.18 trang 49 Toán 12 Tập 2
Trong không gian Oxyz, một viên đạn được bắn ra từ điểm A(1; 3; 4) và trong 3 giây, đầu đạn đi với vận tốc không đổi. Bài 5.18 trang 49 Toán 12 Tập 2

Bài 5.19 trang 49 Toán 12 Tập 2
Trên mặt đất phẳng, người ta dựng một cây cột thẳng cao 6 m vuông góc với mặt đất, có chân cột đặt tại ví trí O trên mặt đất. Bài 5.19 trang 49 Toán 12 Tập 2

Mở đầu trang 41 Toán 12 Tập 2
Trong không gian Oxyz, mắt một người quan sát ở điểm M(2; 3; −4) và vật cần quan sát đặt tại điểm N(−1; 0; 8). Một tấm bìa chắn đường truyền của ánh sáng có dạng hình tròn với tâm O(0; 0; 0), bán kính bằng 3. Mở đầu trang 41 Toán 12 Tập 2

HĐ1 trang 41 Toán 12 Tập 2
Trong không gian, cho điểm M và vectơ khác vectơ – không. Khẳng định nào trong hai khẳng định sau là đúng? Có duy nhất đường thẳng đi qua M và vuông góc với giá của u. HĐ1 trang 41 Toán 12 Tập 2

Luyện tập 1 trang 42 Toán 12 Tập 2
Luyện tập 1 trang 42 Toán 12 Tập 2

HĐ2 trang 42 Toán 12 Tập 2
Trong không gian Oxyz, một vật thể chuyển động với vectơ vận tốc không đổi u = (a; b; c) ≠ vectơ 0 và xuất phát từ điểm A(x0; y0; z0) (H.5.26). HĐ2 trang 42 Toán 12 Tập 2

Luyện tập 2 trang 43 Toán 12 Tập 2
Trong không gian Oxyz, cho đường thẳng ∆. Hãy chỉ ra hai điểm thuộc ∆ và một vectơ chỉ phương của ∆. Viết phương trình tham số của đường thẳng đi qua gốc tọa độ O(0; 0; 0) và có vectơ chỉ phương v = (1; 3; 1). Luyện tập 2 trang 43 Toán 12 Tập 2

HĐ3 trang 43 Toán 12 Tập 2
Trong không gian Oxyz, cho đường thẳng ∆ đi qua điểm A(x0; y0; z0) và có vectơ chỉ phương u = (a; b; c) (a, b, c là các số khác 0). HĐ3 trang 43 Toán 12 Tập 2
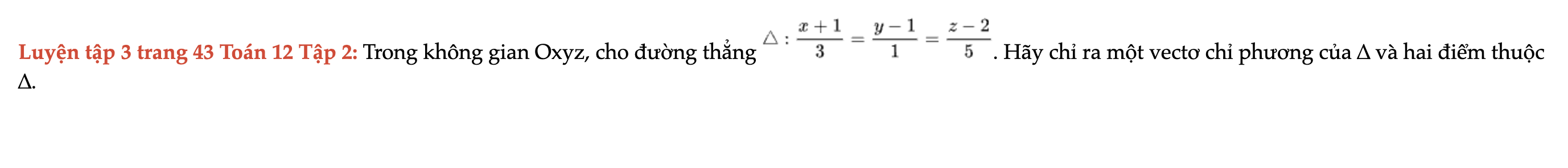
Luyện tập 3 trang 43 Toán 12 Tập 2
Trong không gian Oxyz, cho đường thẳng ∆. Hãy chỉ ra một vectơ chỉ phương của ∆ và hai điểm thuộc ∆. Luyện tập 3 trang 43 Toán 12 Tập 2

Luyện tập 4 trang 44 Toán 12 Tập 2
Trong không gian Oxyz, viết phương trình tham số và phương trình chính tắc của đường thẳng ∆ đi qua điểm A(2; −1; 0) và có vectơ chỉ phương u = (-1; 2; 3). Luyện tập 4 trang 44 Toán 12 Tập 2
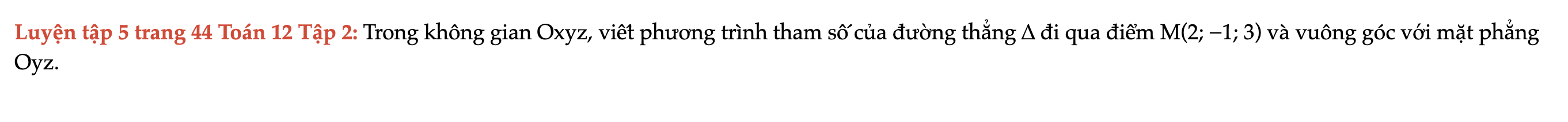
Luyện tập 5 trang 44 Toán 12 Tập 2
Trong không gian Oxyz, viết phương trình tham số của đường thẳng ∆ đi qua điểm M(2; −1; 3) và vuông góc với mặt phẳng Oyz. Luyện tập 5 trang 44 Toán 12 Tập 2

HĐ4 trang 44 Toán 12 Tập 2
Trong không gian Oxyz, cho hai điểm phân biệt A1(x1; y1; z1), A2(x2; y2; z2). Hãy chỉ ra một vectơ chỉ phương của đường thẳng A1A2. Viết phương trình đường thẳng A1A2. HĐ4 trang 44 Toán 12 Tập 2

Luyện tập 6 trang 44 Toán 12 Tập 2
Trong không gian Oxyz, viết phương trình đường thẳng đi qua hai điểm A(2; 1; 3) và B(2; 4; 6). Luyện tập 6 trang 44 Toán 12 Tập 2

Vận dụng 1 trang 45 Toán 12 Tập 2
(H.5.27) Trong tình huống mở đầu hãy thực hiện các bước sau và trả lời câu hỏi đã được nêu ra. Viết phương trình tham số của đường thẳng MN. Tính tọa độ giao điểm D của đường thẳng MN với mặt phẳng Oxy. Vận dụng 1 trang 45 Toán 12 Tập 2

HĐ5 trang 45 Toán 12 Tập 2
Trong không gian Oxyz, cho hai đường thẳng ∆1, ∆2 tương ứng có vectơ chỉ phương u1, u2. HĐ5 trang 45 Toán 12 Tập 2
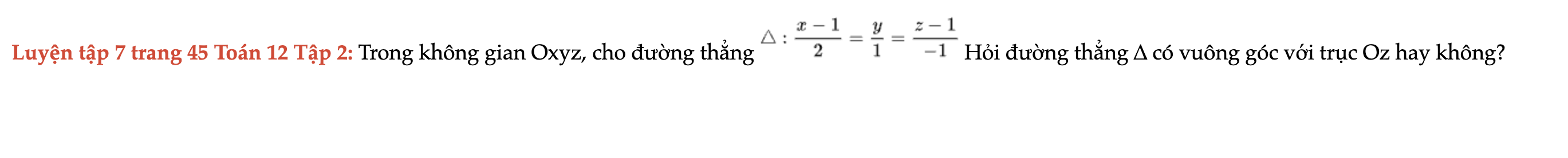
Luyện tập 7 trang 45 Toán 12 Tập 2
Trong không gian Oxyz, cho đường thẳng ∆. Hỏi đường thẳng ∆ có vuông góc với trục Oz hay không? Luyện tập 7 trang 45 Toán 12 Tập 2

Vận dụng 2 trang 45 Toán 12 Tập 2
Tại một nút giao thông có hai con đường. Trên thiết kế, trong không gian Oxyz, hai con đường đó tương ứng thuộc hai đường thẳng Δ1, Δ2. Hỏi hai con đường trên có vuông góc với nhau hay không? Vận dụng 2 trang 45 Toán 12 Tập 2

HĐ6 trang 46 Toán 12 Tập 2
Trong không gian Oxyz, cho hai đường thẳng ∆1; ∆2 lần lượt đi qua các điểm A1(x1; y1; z1), A2(x2; y2; z2) và tương ứng có vectơ chỉ phương u1, u2 (H.5.29). HĐ6 trang 46 Toán 12 Tập 2

Luyện tập 8 trang 46 Toán 12 Tập 2
Trong không gian Oxyz, chứng minh rằng hai đường thẳng sau song song với nhau. Luyện tập 8 trang 46 Toán 12 Tập 2
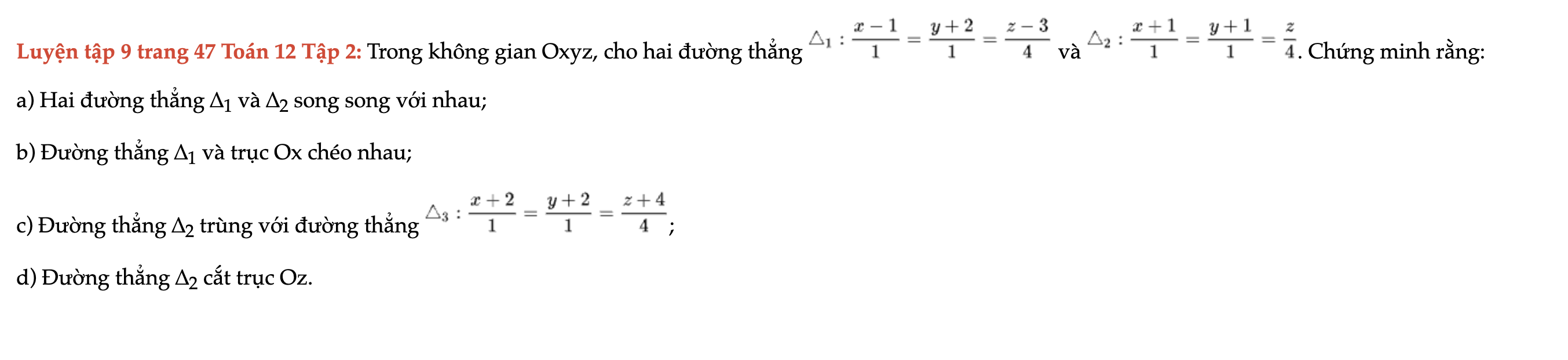
Luyện tập 9 trang 47 Toán 12 Tập 2
Trong không gian Oxyz, cho hai đường thẳng ∆1 và ∆2. Chứng minh rằng hai đường thẳng ∆1 và ∆2 song song với nhau; đường thẳng ∆1 và trục Ox chéo nhau. Luyện tập 9 trang 47 Toán 12 Tập 2

Luyện tập 10 trang 48 Toán 12 Tập 2
Trong không gian Oxyz, xét vị trí tương đối giữa hai đường thẳng ∆1 và ∆2. Luyện tập 10 trang 48 Toán 12 Tập 2

Vận dụng 3 trang 48 Toán 12 Tập 2
(H.5.30) Trong không gian Oxyz, có hai vật thể lần lượt xuất phát từ A(1; 2; 0) và B(3; 5; 0) với vận tốc không đổi tương ứng là v1 = (2; 1; 3), v2 = (1; 2; 1). Vận dụng 3 trang 48 Toán 12 Tập 2
Giải bài tập Bài 16. Công thức tính góc trong không gian.

Bài 5.20 trang 53 Toán 12 Tập 2
Trong không gian Oxyz, tính góc giữa hai đường thẳng. Bài 5.20 trang 53 Toán 12 Tập 2

Bài 5.21 trang 53 Toán 12 Tập 2
Bài 5.21 trang 53 Toán 12 Tập 2
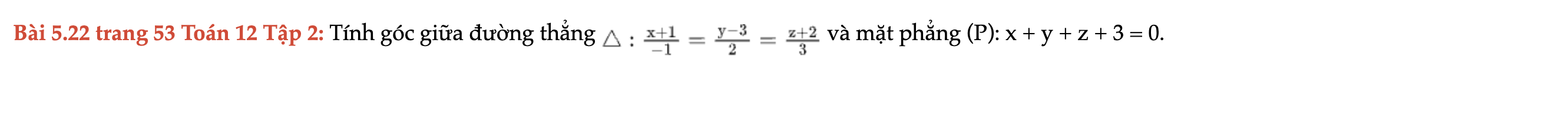
Bài 5.22 trang 53 Toán 12 Tập 2
Tính góc giữa đường thẳng và mặt phẳng (P). Bài 5.22 trang 53 Toán 12 Tập 2

Bài 5.23 trang 53 Toán 12 Tập 2
Kim tự tháp Kheops ở Ai Cập có dạng hình chóp S.ABCD, có đáy là hình vuông với cạnh dài 230 m, các cạnh bên bằng nhau và dài 219 m (H.5.38). Tính góc giữa hai mặt phẳng (SAB) và (SBC). Bài 5.23 trang 53 Toán 12 Tập 2

Bài 5.24 trang 53 Toán 12 Tập 2
Trong một bể hình lập phương cạnh 1 m có chứa một ít nước. Người ta đặt đáy bể nghiêng so với mặt phẳng nằm ngang. Biết rằng, lúc đó mặt nước có dạng hình bình hành ABCD. Bài 5.24 trang 53 Toán 12 Tập 2

Mở đầu trang 50 Toán 12 Tập 2
Một mái nhà hình tròn được đặt trên ba cây cột trụ (H.5.33). Các cây cột vuông góc với mặt sàn nhà phẳng và có độ cao lần lượt là 7 m, 6 m, 5 m. Ba chân cột là ba đỉnh của một tam giác đều trên mặt sàn nhà với cạnh dài 4 m. Mở đầu trang 50 Toán 12 Tập 2

HĐ1 trang 50 Toán 12 Tập 2
Trong không gian Oxyz, cho hai đường thẳng ∆ và ∆' tương ứng có các vectơ chỉ phương u = (a; b; c), u' = (a'; b'; c') (H.5.34). HĐ1 trang 50 Toán 12 Tập 2
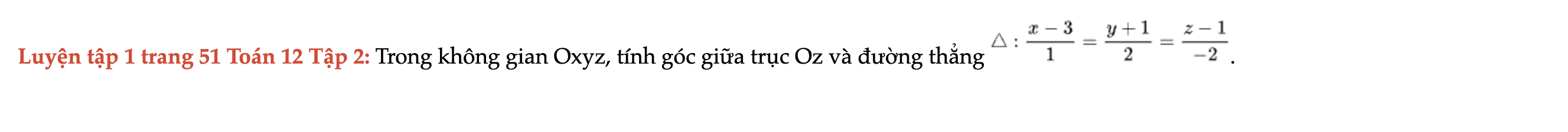
Luyện tập 1 trang 51 Toán 12 Tập 2
Trong không gian Oxyz, tính góc giữa trục Oz và đường thẳng Δ. Luyện tập 1 trang 51 Toán 12 Tập 2

HĐ2 trang 51 Toán 12 Tập 2
Trong không gian Oxyz, cho đường thẳng ∆ và mặt phẳng (P). Xét u = (a; b; c) là một vectơ chỉ phương của ∆ và n = (A; B; C) (với giá ∆') là một vectơ pháp tuyến của (P) (H.5.35). HĐ2 trang 51 Toán 12 Tập 2
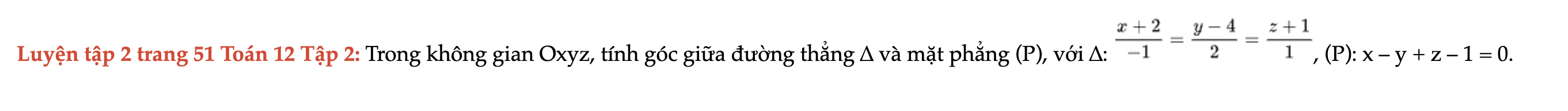
Luyện tập 2 trang 51 Toán 12 Tập 2
Trong không gian Oxyz, tính góc giữa đường thẳng ∆ và mặt phẳng (P), với ∆, (P): x – y + z – 1 = 0. Luyện tập 2 trang 51 Toán 12 Tập 2

HĐ3 trang 52 Toán 12 Tập 2
Trong không gian Oxyz, cho hai mặt phẳng (P), (Q) tương ứng có các vectơ pháp tuyến là n = (A; B; C), n' = (A'; B'; C'). Lấy các đường thẳng ∆, ∆' tương ứng có vectơ chỉ phương n, n' (H.5.36). HĐ3 trang 52 Toán 12 Tập 2
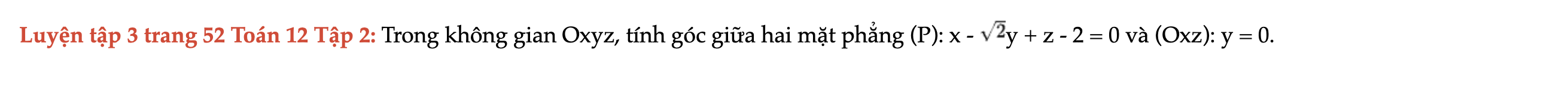
Luyện tập 3 trang 52 Toán 12 Tập 2
Trong không gian Oxyz, tính góc giữa hai mặt phẳng (P) và (Oxz): y = 0. Luyện tập 3 trang 52 Toán 12 Tập 2

Vận dụng trang 53 Toán 12 Tập 2
Hãy trả lời câu hỏi đã được nêu ra trong tình huống mở đầu. Vận dụng trang 53 Toán 12 Tập 2
Giải bài tập Bài 17. Phương trình mặt cầu.

Bài 5.25 trang 59 Toán 12 Tập 2
Bài 5.25 trang 59 Toán 12 Tập 2

Bài 5.26 trang 59 Toán 12 Tập 2
Trong không gian Oxyz, viết phương trình của mặt cầu (S) có tâm I(−2; 0; 5) và bán kính R = 2. Bài 5.26 trang 59 Toán 12 Tập 2

Bài 5.27 trang 59 Toán 12 Tập 2
Trong không gian Oxyz, viết phương trình của mặt cầu (S) có tâm I(0; 3; −1) và có bán kính bằng khoảng cách từ I đến mặt phẳng (P): 3x + 2y – z = 0. Bài 5.27 trang 59 Toán 12 Tập 2
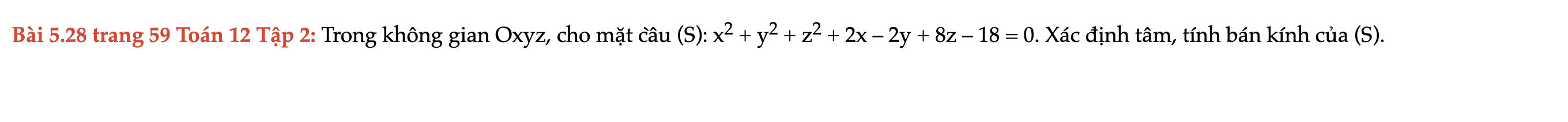
Bài 5.28 trang 59 Toán 12 Tập 2
Trong không gian Oxyz, cho mặt cầu (S): x2 + y2 + z2 + 2x – 2y + 8z – 18 = 0. Xác định tâm, tính bán kính của (S). Bài 5.28 trang 59 Toán 12 Tập 2

Bài 5.29 trang 59 Toán 12 Tập 2
Trong không gian Oxyz, phương trình nào trong các phương trình sau là phương trình mặt cầu? Xác định tâm và tính bán kính của mặt cầu đó. Bài 5.29 trang 59 Toán 12 Tập 2

Bài 5.30 trang 59 Toán 12 Tập 2
Trong không gian Oxyz, một thiết bị phát sóng đặt tại vị trí A(2; 0; 0). Vùng phủ sóng của thiết bị có bán kính bằng 1.Hỏi vị trí M(2; 1; 1) có thuộc vùng phủ sóng của thiết bị nói trên hay không? Bài 5.30 trang 59 Toán 12 Tập 2

Mở đầu trang 54 Toán 12 Tập 2
Bằng ứng dụng Google Maps, thực hiện phép đo khoảng cách trên bề mặt Trái Đất từ vị trí 10°N, 15°E đến vị trí 80°N, 70°E ta sẽ được khoảng cách 8271,74 km (H.5.40). Cơ sở toán học cho việc thiết lập phần mềm tính công thức khoảng cách trên bề mặt Trái Đất
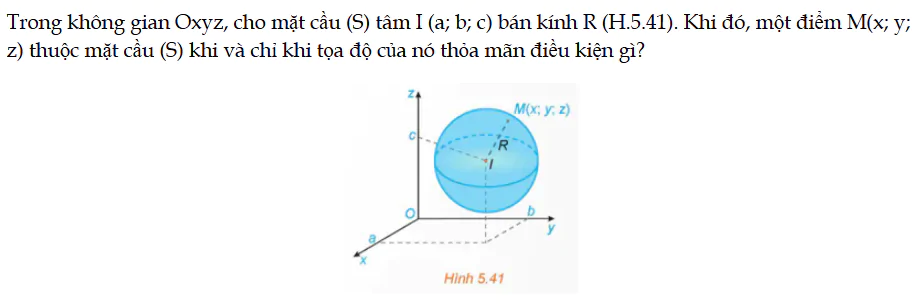
HĐ trang 54 Toán 12 Tập 2
Trong không gian Oxyz, cho mặt cầu (S) tâm I (a; b; c) bán kính R (H.5.41). Khi đó, một điểm M(x; y; z) thuộc mặt cầu (S) khi và chỉ khi tọa độ của nó thỏa mãn điều kiện gì? HĐ trang 54 Toán 12 Tập 2

Luyện tập 1 trang 55 Toán 12 Tập 2
Trong không gian Oxyz, cho mặt cầu (S) có phương trình sau. Luyện tập 1 trang 55 Toán 12 Tập 2

Luyện tập 2 trang 55 Toán 12 Tập 2
Trong không gian Oxyz, viết phương trình mặt cầu (S) trong các trường hợp sau: Luyện tập 2 trang 55 Toán 12 Tập 2

Luyện tập 3 trang 56 Toán 12 Tập 2
Trong không gian Oxyz, cho (S) là tập hợp các điểm M(x; y; z) có tọa độ thỏa mãn phương trình (S): x2 + y2 + z2 – 4x + 6y – 12 = 0. Chứng minh rằng (S) là một mặt cầu. Xác định tâm và tính bán kính của mặt cầu đó. Luyện tập 3 trang 56 Toán 12 Tập 2

Luyện tập 4 trang 56 Toán 12 Tập 2
Trong không gian Oxyz, cho mặt cầu (S) có phương trình, xác định tâm, tính bán kính của (S). Luyện tập 4 trang 56 Toán 12 Tập 2

Luyện tập 5 trang 58 Toán 12 Tập 2
Tính khoảng cách trên mặt đất từ vị trí A là giao giữa kinh tuyến gốc với xích đạo đến vị trí B: 45°N, 30°E. Luyện tập 5 trang 58 Toán 12 Tập 2

Trải nghiệm trang 58 Toán 12 Tập 2
Trên Google Maps, thực hiện phép đo khoảng cách từ vị trí 0°N, 0°E đến vị trí 45°N, 30°E và so sánh với kết quả tính được ở luyện tập 5. Trải nghiệm trang 58 Toán 12 Tập 2
Giải bài tập Bài tập cuối chương 5.

Bài 5.31 trang 61 Toán 12 Tập 2
Trong không gian Oxyz, cho mặt phẳng (P): x – 2y – 3z + 1 = 0. Một vectơ pháp tuyến của mặt phẳng (P) có tọa độ là. Bài 5.31 trang 61 Toán 12 Tập 2

Bài 5.32 trang 61 Toán 12 Tập 2
Trong không gian Oxyz, phương trình mặt phẳng (P) đi qua điểm I(1; −1; 2) và có vectơ n làm vectơ pháp tuyến. Bài 5.32 trang 61 Toán 12 Tập 2
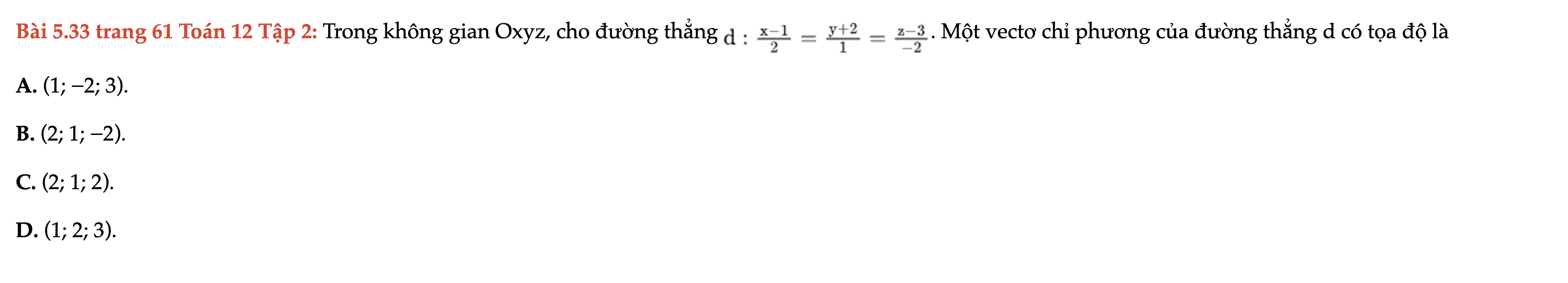
Bài 5.33 trang 61 Toán 12 Tập 2
Trong không gian Oxyz, cho đường thẳng d. Một vectơ chỉ phương của đường thẳng d có tọa độ là. Bài 5.33 trang 61 Toán 12 Tập 2
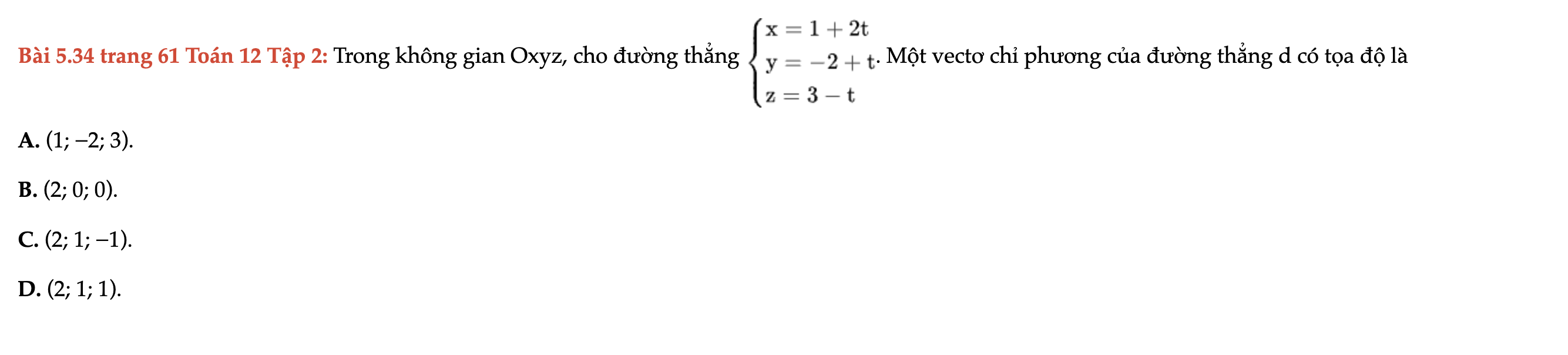
Bài 5.34 trang 61 Toán 12 Tập 2
Bài 5.34 trang 61 Toán 12 Tập 2

Bài 5.35 trang 61 Toán 12 Tập 2
Trong không gian Oxyz, phương trình đường thẳng d đi qua I(2; −1; 1) và nhận vectơ u làm vectơ chỉ phương. Bài 5.35 trang 61 Toán 12 Tập 2

Bài 5.36 trang 61 Toán 12 Tập 2
Trong không gian Oxyz, cho hai điểm A(−1; 0; −1), B(2; 1; 1). Phương trình đường thẳng AB là. Bài 5.36 trang 61 Toán 12 Tập 2

Bài 5.37 trang 61 Toán 12 Tập 2
Trong không gian Oxyz, phương trình đường thẳng d đi qua I(2; 1; −3) và vuông góc với mặt phẳng (P): x – 2y + z – 3 = 0 là. Bài 5.37 trang 61 Toán 12 Tập 2
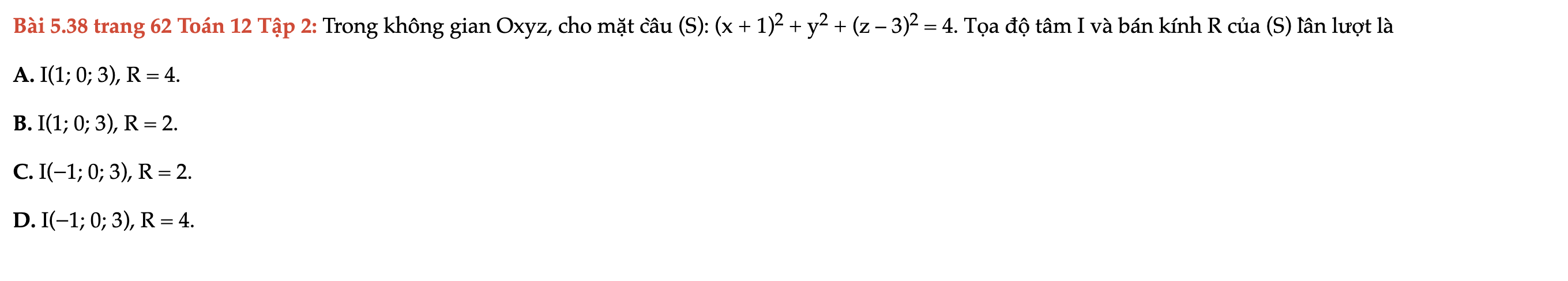
Bài 5.38 trang 62 Toán 12 Tập 2
Trong không gian Oxyz, cho mặt cầu (S), tọa độ tâm I và bán kính R của (S) lần lượt là. Bài 5.38 trang 62 Toán 12 Tập 2
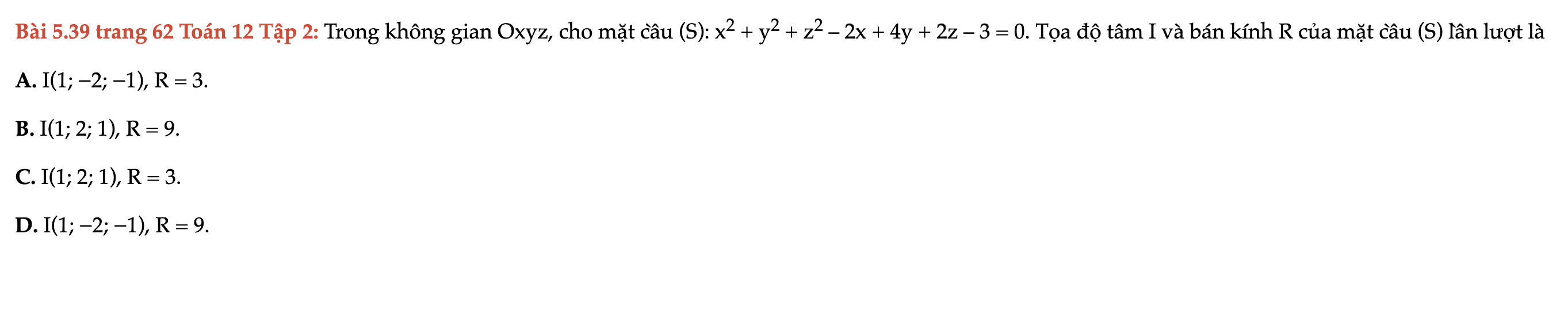
Bài 5.39 trang 62 Toán 12 Tập 2
Trong không gian Oxyz, cho mặt cầu (S), tọa độ tâm I và bán kính R của mặt cầu (S) lần lượt là. Bài 5.39 trang 62 Toán 12 Tập 2

Bài 5.40 trang 62 Toán 12 Tập 2
Trong không gian Oxyz, cho ba điểm A(1; 0; −1), B(0; 1; 2), C(−1; −2; 3). Bài 5.40 trang 62 Toán 12 Tập 2
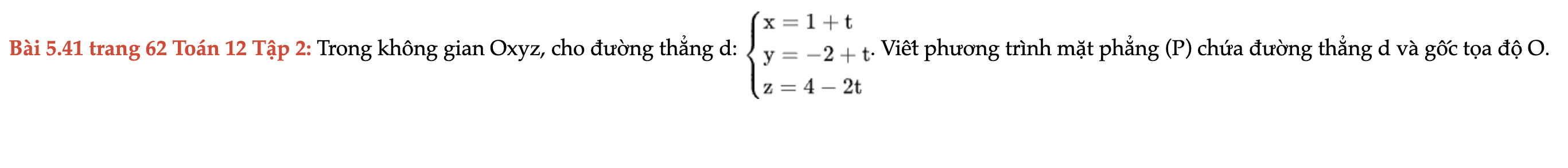
Bài 5.41 trang 62 Toán 12 Tập 2
Trong không gian Oxyz, cho đường thẳng d, viết phương trình mặt phẳng (P) chứa đường thẳng d và gốc tọa độ O. Bài 5.41 trang 62 Toán 12 Tập 2

Bài 5.42 trang 62 Toán 12 Tập 2
Trong không gian Oxyz, cho mặt phẳng (P): x – 2y + 2z – 1 = 0 và hai điểm A(1; −1; 2), B(−1; 1; 0). Bài 5.42 trang 62 Toán 12 Tập 2

Bài 5.43 trang 62 Toán 12 Tập 2
Trong không gian Oxyz, cho điểm A(1; 0; 2) và hai đường thẳng xét vị trí tương đối của hai đường thẳng d và d'. Bài 5.43 trang 62 Toán 12 Tập 2
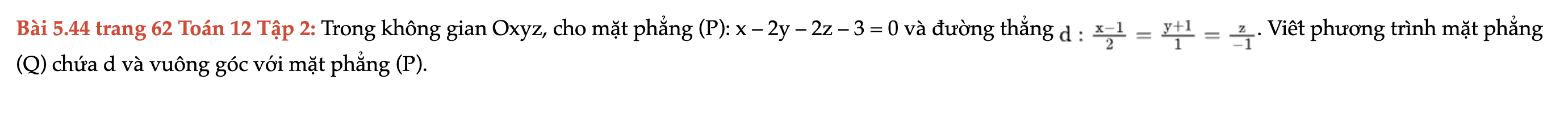
Bài 5.44 trang 62 Toán 12 Tập 2
Trong không gian Oxyz, cho mặt phẳng (P): x – 2y – 2z – 3 = 0 và đường thẳng d, viết phương trình mặt phẳng (Q) chứa d và vuông góc với mặt phẳng (P). Bài 5.44 trang 62 Toán 12 Tập 2
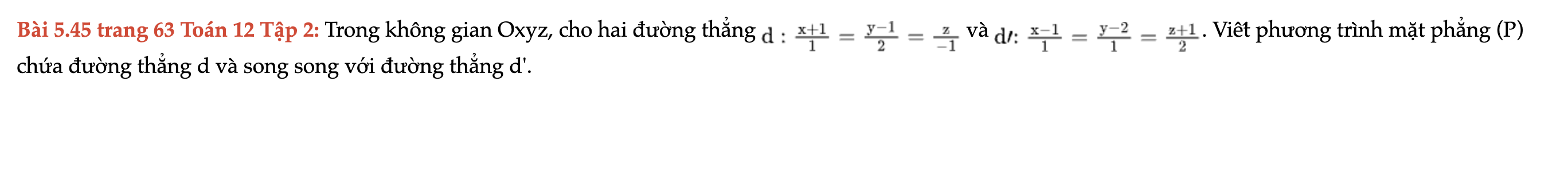
Bài 5.45 trang 63 Toán 12 Tập 2
Trong không gian Oxyz, cho hai đường thẳng, viết phương trình mặt phẳng (P) chứa đường thẳng d và song song với đường thẳng d'. Bài 5.45 trang 63 Toán 12 Tập 2
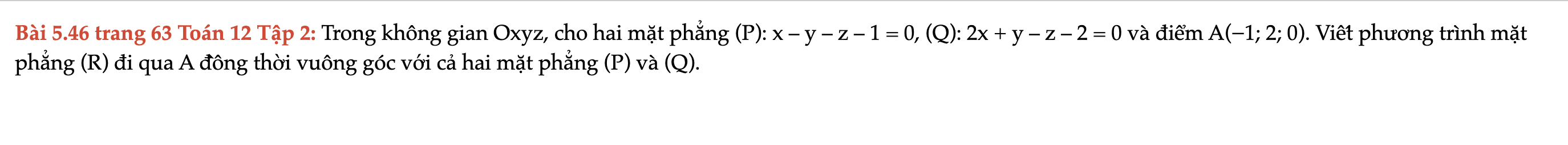
Bài 5.46 trang 63 Toán 12 Tập 2
Trong không gian Oxyz, cho hai mặt phẳng (P): x – y – z – 1 = 0, (Q): 2x + y – z – 2 = 0 và điểm A(−1; 2; 0). Viết phương trình mặt phẳng (R) đi qua A đồng thời vuông góc với cả hai mặt phẳng (P) và (Q). Bài 5.46 trang 63 Toán 12 Tập 2
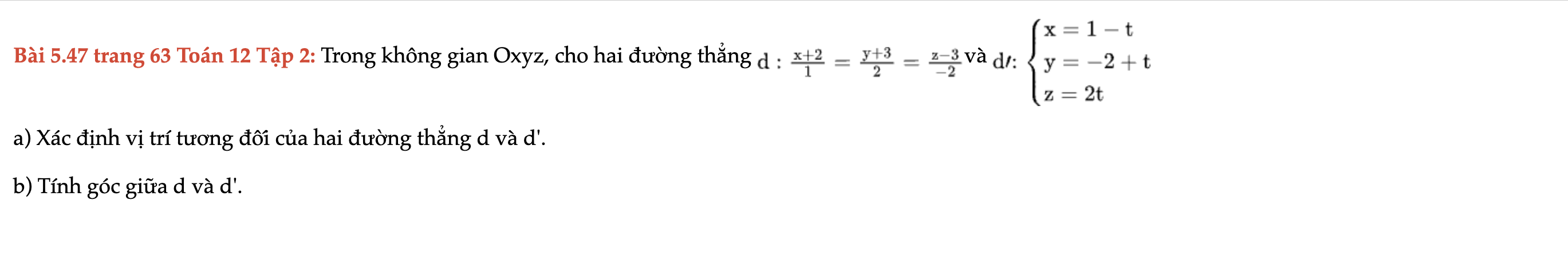
Bài 5.47 trang 63 Toán 12 Tập 2
Trong không gian Oxyz, cho hai đường thẳng xác định vị trí tương đối của hai đường thẳng d và d'. Bài 5.47 trang 63 Toán 12 Tập 2

Bài 5.48 trang 63 Toán 12 Tập 2
Trong không gian Oxyz, tính góc tạo bởi đường thẳng d và mặt phẳng (P): x + y – 2z + 3 = 0. Bài 5.48 trang 63 Toán 12 Tập 2
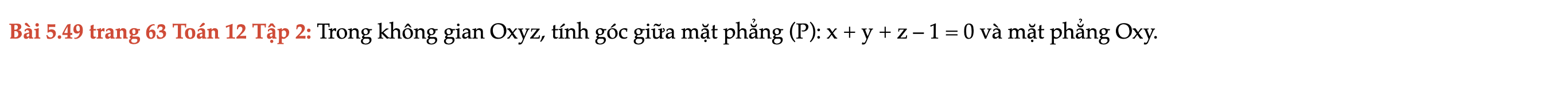
Bài 5.49 trang 63 Toán 12 Tập 2
Trong không gian Oxyz, tính góc giữa mặt phẳng (P): x + y + z – 1 = 0 và mặt phẳng Oxy. Bài 5.49 trang 63 Toán 12 Tập 2

Bài 5.50 trang 63 Toán 12 Tập 2
Từ mặt nước trong một bể nước, tại ba vị trí đôi một cách nhau 2 m, người ta lần lượt thả dây dọi để quả dọi chạm đáy bể. Phần dây dọi (thẳng) nằm trong nước tại ba vị trí đó lần lượt có độ dài 4 m; 4,4 m; 4,8 m. Bài 5.50 trang 63 Toán 12 Tập 2

Bài 5.51 trang 63 Toán 12 Tập 2
Bản vẽ thiết kế của một công trình được vẽ trong một hệ trục tọa độ Oxyz. Sàn nhà của công trình thuộc mặt phẳng Oxy, đường ống thoát nước thẳng và đi qua hai điểm A(1; 2; −1); B(5; 6; −2); tính góc giữa đường ống thoát sàn Bài 5.51 trang 63 Toán 12 Tập 2

Bài 5.52 trang 63 Toán 12 Tập 2
Nếu đứng trước biển và nhìn ra xa, người ta sẽ thấy một đường giao giữa mặt biển và bầu trời, đó là đường chân trời đối với người quan sát (H.5.45a). Bài 5.52 trang 63 Toán 12 Tập 2