Giải bài tập Toán 12 Chương 1. Ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số | Kết Nối Tri Thức
Hướng dẫn giải chi tiết từng bước bài tập thuộc Chương 1. Ứng dụng đạo hàm để khảo sát hàm số. Đạo hàm, bảng biến thiên, đồng biến nghịch biến, cực trị, min, max, tiệm cận đứng, tiệm cận ngang, tiệm cận xiên sách giáo khoa Chân trời sáng tạo.
Giải bài tập Bài 1. Tính đơn điệu và cực trị của hàm số.
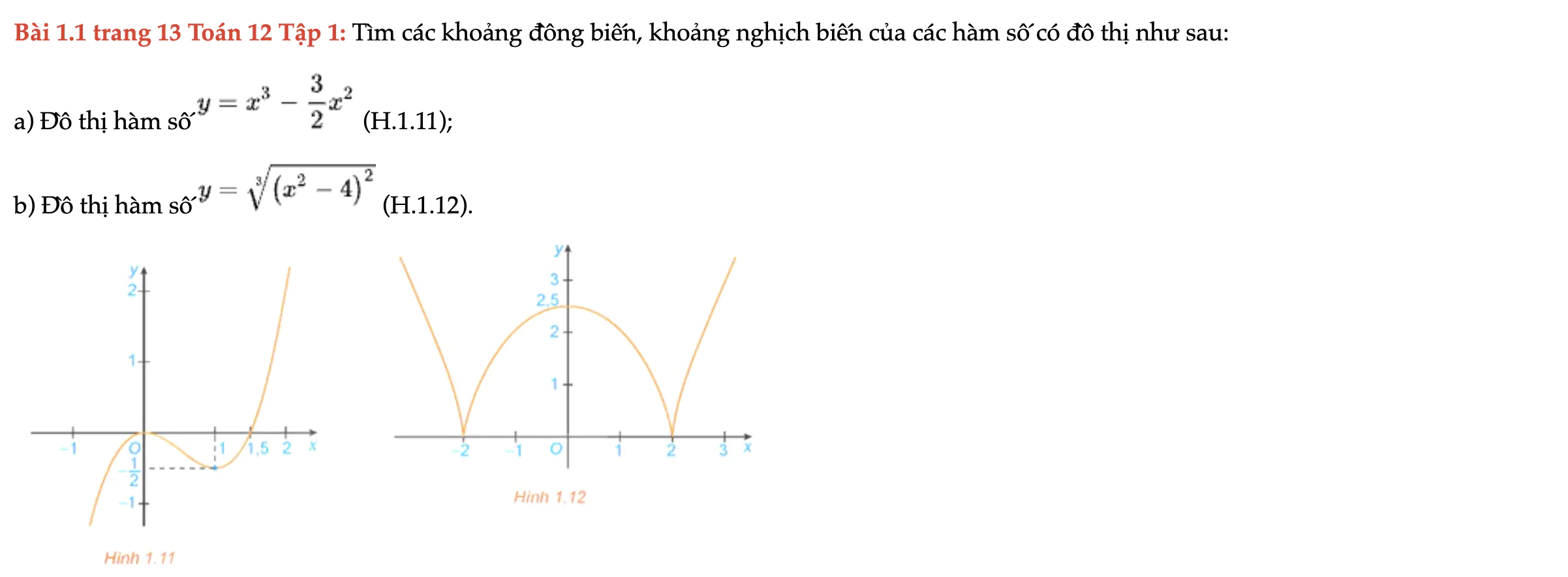
Bài 1.1 trang 13 Toán 12 Tập 1
Tìm các khoảng đồng biến, khoảng nghịch biến của các hàm số có đồ thị như sau. Bài 1.1 trang 13 Toán 12 Tập 1

Bài 1.2 trang 13 Toán 12 Tập 1
Xét sự đồng biến, nghịch biến của các hàm số sau. Bài 1.2 trang 13 Toán 12 Tập 1

Bài 1.3 trang 13 Toán 12 Tập 1
Tìm các khoảng đơn điệu của các hàm số sau. Bài 1.3 trang 13 Toán 12 Tập 1

Bài 1.4 trang 13 Toán 12 Tập 1
Xét chiều biến thiên của các hàm số sau. Bài 1.4 trang 13 Toán 12 Tập 1

Bài 1.5 trang 13 Toán 12 Tập 1
Giả sử số dân của một thị trấn sau t năm kể từ năm 2000 được mô tả bởi hàm số; tính số dân của thị trấn đó vào các năm 2000 và 2015. Bài 1.5 trang 13 Toán 12 Tập 1

Bài 1.6 trang 14 Toán 12 Tập 1
Đồ thị của đạo hàm bậc nhất y = f'(x) của hàm số f(x) được cho trong hình 1.13. Bài 1.6 trang 14 Toán 12 Tập 1
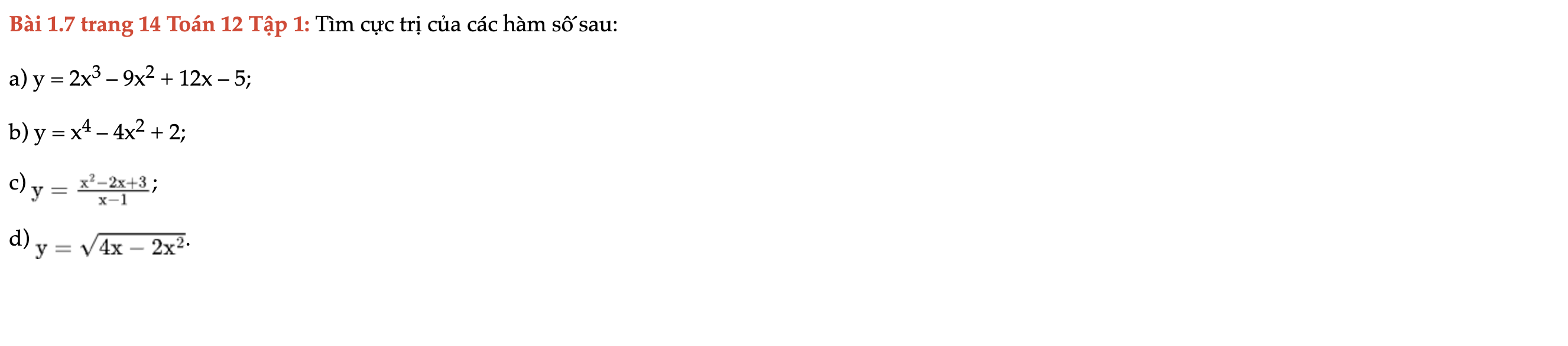
Bài 1.7 trang 14 Toán 12 Tập 1
Tìm cực trị của các hàm số sau. Bài 1.7 trang 14 Toán 12 Tập 1

Bài 1.8 trang 14 Toán 12 Tập 1
Cho hàm số y = f(x) = |x|. Bài 1.8 trang 14 Toán 12 Tập 1

Bài 1.9 trang 14 Toán 12 Tập 1
Giả sử doanh số (tính bằng số sản phẩm) của một sản phẩm mới (trong vòng một số năm nhất định) tuân theo quy luật logistic được mô hình hóa bằng hàm số, hỏi sau khi phát hành bao nhiêu năm thì tốc độ bán hàng là lớn nhất. Bài 1.9 trang 14 Toán 12 Tập 1

Mở đầu trang 5 Toán 12 Tập 1
Xét một chất điểm chuyển động trên một trục số nằm ngang, chiều dương từ trái sang phải (H.1.1). Giả sử vị trí s(t) (mét) của chất điểm trên trục số đã chọn tại thời điểm t (giây) được cho bởi công thức. Mở đầu trang 5 Toán 12 Tập 1
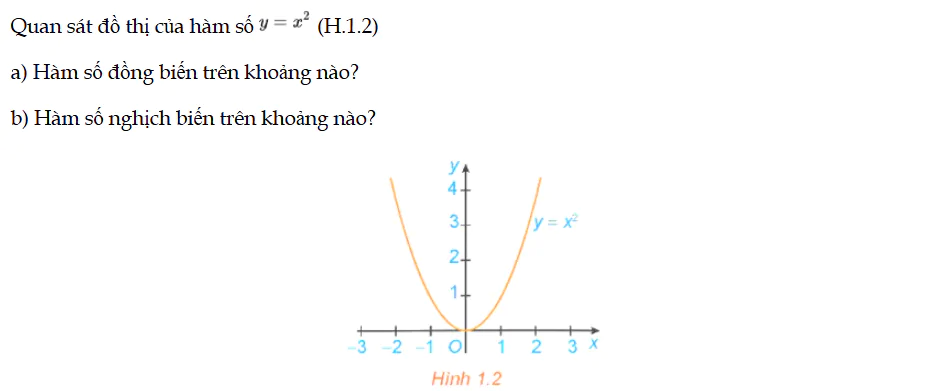
HĐ1 trang 6 Toán 12 Tập 1
Quan sát đồ thị của hàm số (H.1.2). Hàm số đồng biến, nghịch biến trên khoảng nào? HĐ1 trang 6 Toán 12 Tập 1
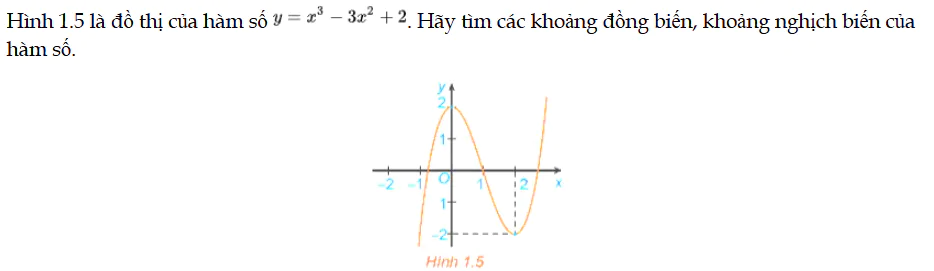
Luyện tập 1 trang 6 Toán 12 Tập 1
Hình 1.5 là đồ thị của hàm số y = f(x), hãy tìm các khoảng đồng biến, khoảng nghịch biến của hàm số. Luyện tập 1 trang 6 Toán 12 Tập 1
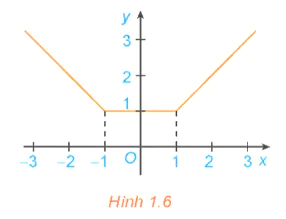
HĐ2 trang 7 Toán 12 Tập 1
Xét hàm số y = f(x) có đồ thị như hình 1.6. HĐ2 trang 7 Toán 12 Tập 1

Luyện tập 2 trang 7 Toán 12 Tập 1
Tìm các khoảng đồng biến, khoảng nghịch biến của hàm số y = f(x). Luyện tập 2 trang 7 Toán 12 Tập 1

HĐ3 trang 7 Toán 12 Tập 1
Cho hàm số y = f(x), thực hiện các yêu cầu đề bài. HĐ3 trang 7 Toán 12 Tập 1

Luyện tập 3 trang 9 Toán 12 Tập 1
Tìm các khoảng đơn điệu của các hàm số sau. Luyện tập 3 trang 9 Toán 12 Tập 1

Vận dụng 1 trang 9 Toán 12 Tập 1
Giải bài toán trong tình huống mở đầu bằng cách thực hiện lần lượt các yêu cầu sau. Vận dụng 1 trang 9 Toán 12 Tập 1
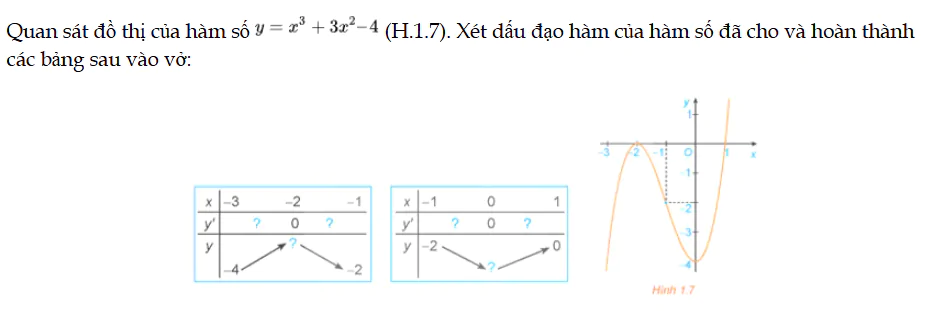
HĐ4 trang 9 Toán 12 Tập 1
Quan sát đồ thị của hàm số y = f(x), xét dấu đạo hàm của hàm số đã cho và hoàn thành các bảng sau vào vở. HĐ4 trang 9 Toán 12 Tập 1
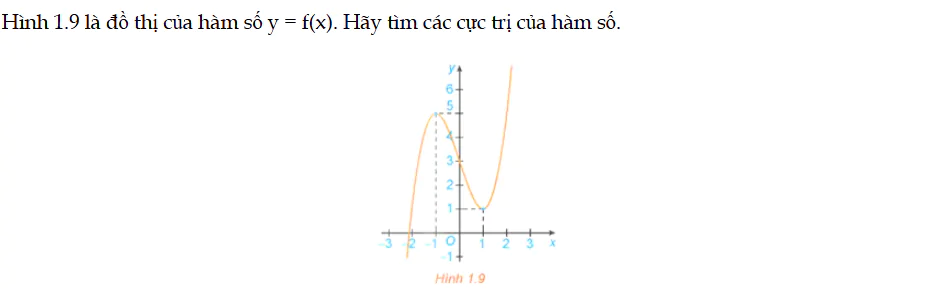
Luyện tập 4 trang 10 Toán 12 Tập 1
Hình 1.9 là đồ thị của hàm số y = f(x). Hãy tìm các cực trị của hàm số. Luyện tập 4 trang 10 Toán 12 Tập 1

HĐ5 trang 10 Toán 12 Tập 1
Cho hàm số y = f(x), a) Tính đạo hàm f'(x) và tìm các điểm mà tại đó đạo hàm f'(x) = 0. b) Lập bảng biến thiên của hàm số. c) Từ bảng biến thiên suy ra các điểm cực trị của hàm số. HĐ5 trang 10 Toán 12 Tập 1
Câu hỏi trang 11 Toán 12 Tập 1
Giải thích vì sao nếu f'(x) không đổi dấu khi x qua x0 thì x0 không phải là điểm cực trị của hàm số f(x)? Câu hỏi trang 11 Toán 12 Tập 1

Luyện tập 5 trang 12 Toán 12 Tập 1
Tìm cực trị của các hàm số sau.Luyện tập 5 trang 12 Toán 12 Tập 1

Vận dụng 2 trang 12 Toán 12 Tập 1
Một vật được phóng thẳng đứng lên trên từ độ cao 2m với vận tốc ban đầu là 24,5 m/s. Trong Vật lí, ta biết rằng khi bỏ qua sức cản của không khí thì độ cao h của vật sau t (giây) được cho bởi công thức. Hỏi tại thời điểm nào thì vật đạt độ cao lớn nhất?
Giải bài tập Bài 2. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số.

Bài 1.10 trang 19 Toán 12 Tập 1
Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của các hàm số sau. Bài 1.10 trang 19 Toán 12 Tập 1

Bài 1.11 trang 19 Toán 12 Tập 1
Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của các hàm số sau. Bài 1.11 trang 19 Toán 12 Tập 1

Bài 1.12 trang 19 Toán 12 Tập 1
Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau. Bài 1.12 trang 19 Toán 12 Tập 1

Bài 1.13 trang 19 Toán 12 Tập 1
Trong các hình chữ nhật có chu vi là 24 cm, hãy tìm hình chữ nhật có diện tích lớn nhất. Bài 1.13 trang 19 Toán 12 Tập 1

Bài 1.14 trang 19 Toán 12 Tập 1
Một nhà sản xuất muốn thiết kế một chiếc hộp có dạng hình hộp chữ nhật không có nắp, có đáy là hình vuông; tìm các kích thước của chiếc hộp sao cho thể tích của hộp là lớn nhất. Bài 1.14 trang 19 Toán 12 Tập 1

Bài 1.15 trang 19 Toán 12 Tập 1
Bài 1.15 trang 19 Toán 12 Tập 1. Tính các kích thước của bình để chi phí vật liệu sản xuất mỗi chiếc bình là nhỏ nhất.
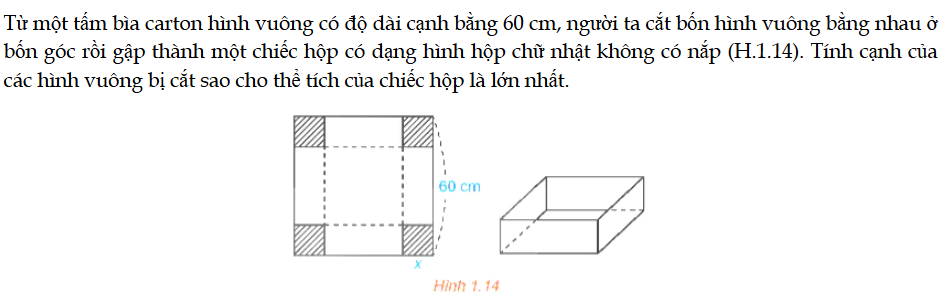
Mở đầu trang 15 Toán 12 Tập 1
Từ một tấm bìa carton hình vuông có độ dài cạnh bằng 60 cm, người ta cắt bốn hình vuông bằng nhau ở bốn góc rồi gập thành một chiếc hộp có dạng hình hộp chữ nhật không có nắp (H.1.14). Tính cạnh của các hình vuông bị cắt sao cho thể tích của chiếc hộp là
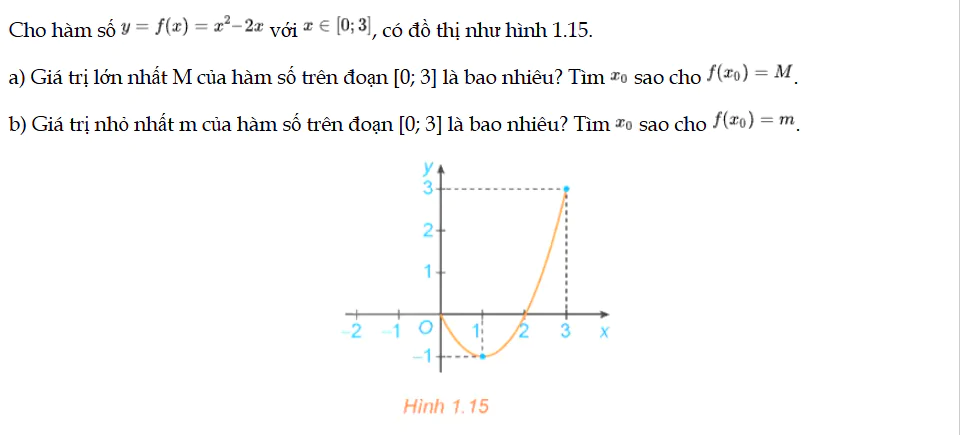
HĐ1 trang 15 Toán 12 Tập 1
Cho hàm số y = f(x), có đồ thị như hình 1.15. HĐ1 trang 15 Toán 12 Tập 1

Luyện tập 1 trang 17 Toán 12 Tập 1
Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của các hàm số sau: Luyện tập 1 trang 17 Toán 12 Tập 1

HĐ2 trang 17 Toán 12 Tập 1
Xét hàm số y = f(x) trên đoạn [−1; 2] với đồ thị như hình 1.16. HĐ2 trang 17 Toán 12 Tập 1

Luyện tập 2 trang 18 Toán 12 Tập 1
Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau. Luyện tập 2 trang 18 Toán 12 Tập 1

Vận dụng trang 18 Toán 12 Tập 1
Giả sử sự lây lan của một loại virus ở một địa phương có thể được mô hình hóa bằng hàm số N(t), trong đó N là số người bị nhiễm bệnh (tính bằng trăm người) và t là thời gian (tuần). Vận dụng trang 18 Toán 12 Tập 1
Giải bài tập Bài 3. Đường tiệm cận của đồ thị hàm số.
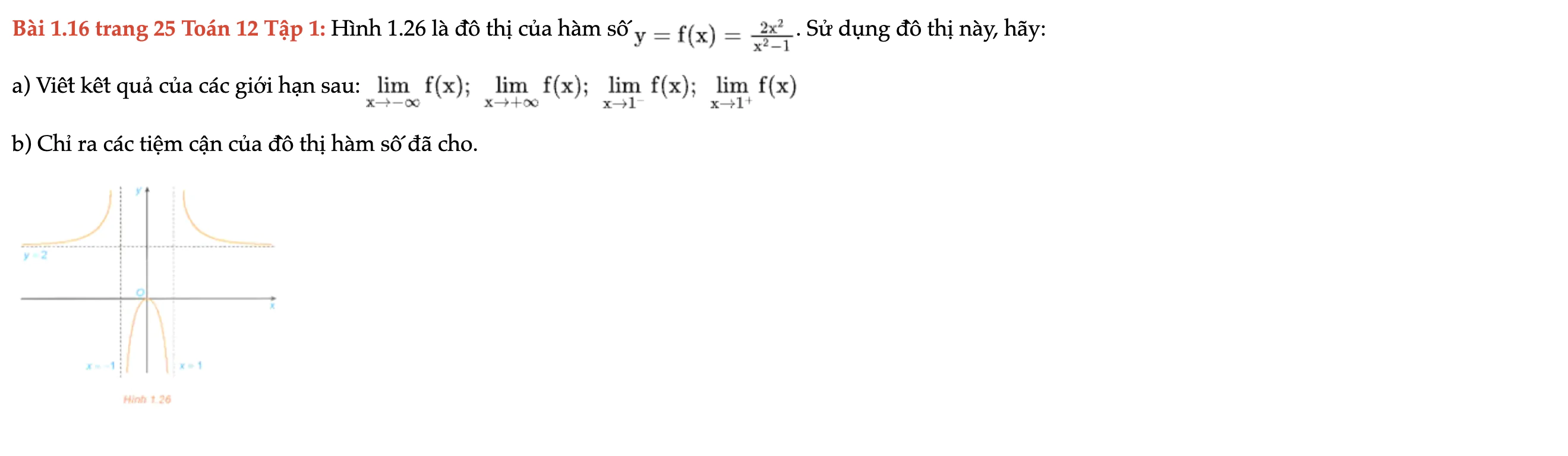
Bài 1.16 trang 25 Toán 12 Tập 1
Hình 1.26 là đồ thị của hàm số; chỉ ra các tiệm cận của đồ thị hàm số đã cho. Bài 1.16 trang 25 Toán 12 Tập 1

Bài 1.17 trang 25 Toán 12 Tập 1
Đường thẳng x = 1 có phải là tiệm cận đứng của đồ thị hàm số không. Bài 1.17 trang 25 Toán 12 Tập 1

Bài 1.18 trang 25 Toán 12 Tập 1
Tìm các tiệm cận của đồ thị các hàm số sau. Bài 1.18 trang 25 Toán 12 Tập 1
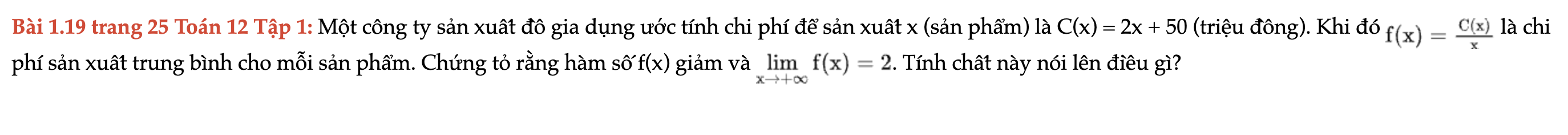
Bài 1.19 trang 25 Toán 12 Tập 1
Một công ty sản xuất đồ gia dụng ước tính chi phí để sản xuất x (sản phẩm) là C(x) = 2x + 50 (triệu đồng). Bài 1.19 trang 25 Toán 12 Tập 1

Bài 1.20 trang 25 Toán 12 Tập 1
Một mảnh vườn hình chữ nhật có diện tích bằng 144 m2, biết độ dài một cạnh của mảnh vườn là x (m); viết biểu thức tính chu vi P(x) mét của mảnh vườn. Bài 1.20 trang 25 Toán 12 Tập 1
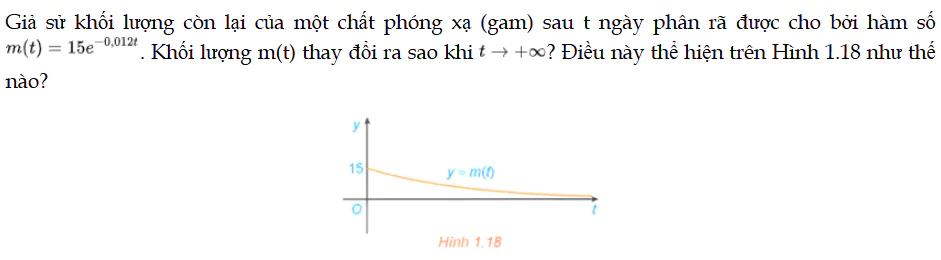
Mở đầu trang 20 Toán 12 Tập 1
Giả sử khối lượng còn lại của một chất phóng xạ (gam) sau t ngày phân rã được cho bởi hàm số m(t). Khối lượng m(t) thay đổi ra sao khi, điều này thể hiện trên Hình 1.18 như thế nào? Mở đầu trang 20 Toán 12 Tập 1
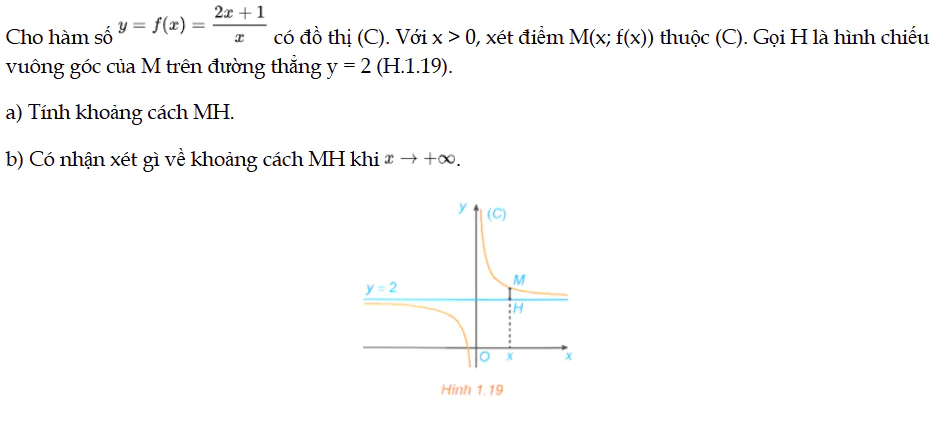
HĐ1 trang 20 Toán 12 Tập
Cho hàm số y = f(x) có đồ thị (C). Với x > 0, xét điểm M(x; f(x)) thuộc (C). Gọi H là hình chiếu vuông góc của M trên đường thẳng y = 2 (H.1.19). HĐ1 trang 20 Toán 12 Tập
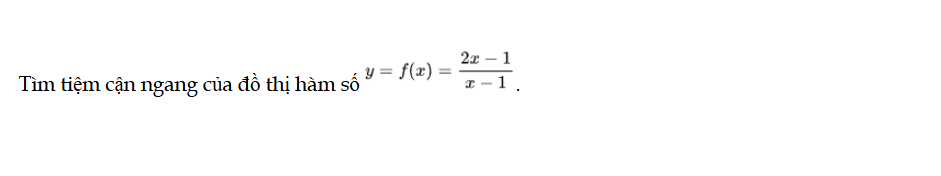
Luyện tập 1 trang 21 Toán 12 Tập 1
Tìm tiệm cận ngang của đồ thị hàm số y = f(x). Luyện tập 1 trang 21 Toán 12 Tập 1

Vận dụng 1 trang 21 Toán 12 Tập 1
Giải bài toán trong tình huống mở đầu. Vận dụng 1 trang 21 Toán 12 Tập 1
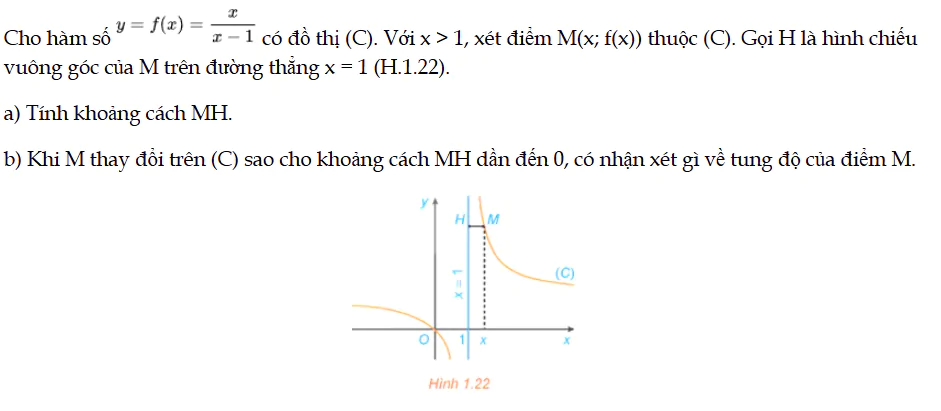
HĐ2 trang 21 Toán 12 Tập 1
Cho hàm số y = f(x) có đồ thị (C). Với x > 1, xét điểm M(x; f(x)) thuộc (C). Gọi H là hình chiếu vuông góc của M trên đường thẳng x = 1 (H.1.22). HĐ2 trang 21 Toán 12 Tập 1

Luyện tập 2 trang 22 Toán 12 Tập 1
Tìm các tiệm cận ngang và tiệm cận đứng của đồ thị hàm số y = f(x). Luyện tập 2 trang 22 Toán 12 Tập 1

Vận dụng 2 trang 22 Toán 12 Tập 1
Để loại bỏ p% một loài tảo độc khỏi một hồ nước, người ta ước tính chi phí bỏ ra là C(p). Tìm tiệm cận đứng của đồ thị hàm số C(p) và nêu ý nghĩa thực tiễn của đường tiệm cận này. Vận dụng 2 trang 22 Toán 12 Tập 1

HĐ3 trang 23 Toán 12 Tập 1
Cho hàm số y = f(x) có đồ thị (C) và đường thẳng y = x −1 như hình 1.24. HĐ3 trang 23 Toán 12 Tập 1

Luyện tập 3 trang 24 Toán 12 Tập 1
Tìm các tiệm cận đứng và tiệm cận xiên của đồ thị hàm số y = f(x). Luyện tập 3 trang 24 Toán 12 Tập 1
Giải bài tập Bài 4. Khảo sát sự biến thiên và vẽ đồ thị của hàm số.

Bài 1.21 trang 32 Toán 12 Tập 1
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau. Bài 1.21 trang 32 Toán 12 Tập 1

Bài 1.22 trang 32 Toán 12 Tập 1
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau. Bài 1.22 trang 32 Toán 12 Tập 1

Bài 1.24 trang 32 Toán 12 Tập 1
Một cốc chứa 30 ml dung dịch KOH (potassium hydroxide) với nồng độ 100 mg/ml. Một bình chứa dung dịch KOH khác với nồng độ 8 mg/ml được trộn vào cốc. Bài 1.24 trang 32 Toán 12 Tập 1

Bài 1.25 trang 32 Toán 12 Tập 1
Giả sử một điện trở 8 W được mắc song song với một biến trở như Hình 1.33. Nếu điện trở đó được kí hiệu x (W) thì điện trở tương đương R là hàm số của x. Vẽ đồ thị của hàm số y = R(x), x > 0 và dựa vào đồ thị đã vẽ. Bài 1.25 trang 32 Toán 12 Tập 1

Bài 1.23 trang 32 Toán 12 Tập 1
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau. Bài 1.23 trang 32 Toán 12 Tập 1
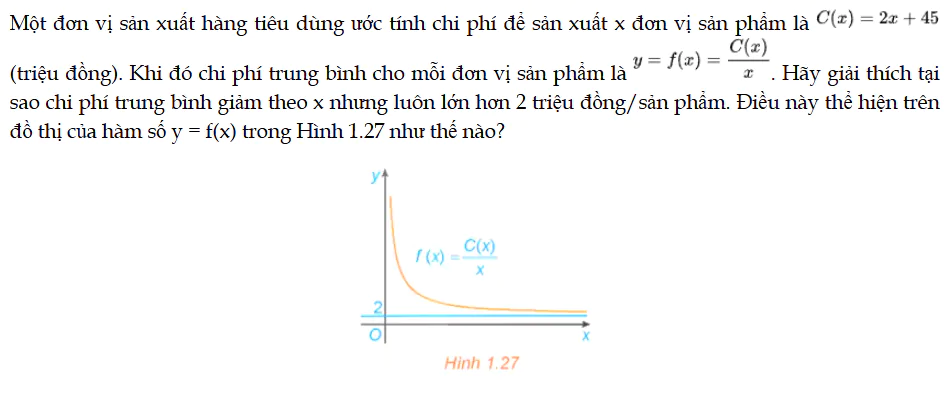
Mở đầu trang 26 Toán 12 Tập 1
Một đơn vị sản xuất hàng tiêu dùng ước tính chi phí để sản xuất x đơn vị sản phẩm là C(x) = 2x + 45 (triệu đồng). Khi đó chi phí trung bình cho mỗi đơn vị sản phẩm là y =f(x). Mở đầu trang 26 Toán 12 Tập 1

HĐ1 trang 26 Toán 12 Tập 1
Cho hàm số y = f(x). Thực hiện lần lượt các yêu cầu sau. HĐ1 trang 26 Toán 12 Tập 1

Luyện tập 1 trang 28 Toán 12 Tập 1
Khảo sát sự biến thiên và vẽ đồ thị của hàm số y = f(x). Luyện tập 1 trang 28 Toán 12 Tập 1

Luyện tập 2 trang 29 Toán 12 Tập 1
Giải bài toán ở tình huống mở đầu, coi f(x) là hàm số xác định với x lớn hơn hoặc bằng 1. Luyện tập 2 trang 29 Toán 12 Tập 1

Vận dụng trang 29 Toán 12 Tập 1
Một bể chứa ban đầu có 200 lít nước. Sau đó, cứ mỗi phút người ta bơm thêm 40 lít nước, đồng thời cho vào bể 20 gam chất khử trùng (hòa tan). Vận dụng trang 29 Toán 12 Tập 1

Luyện tập 3 trang 32 Toán 12 Tập 1
Khảo sát sự biến thiên và vẽ đồ thị của hàm số y = f(x). Luyện tập 3 trang 32 Toán 12 Tập 1
Giải bài tập Bài 5. Ứng dụng đạo hàm để giải quyết một số vấn đề liên quan đến thực tiễn.

Bài 1.26 trang 40 Toán 12 Tập 1
Giả sử một hạt chuyển động trên một trục thẳng đứng chiều dương hướng lên trên sao cho tọa độ của hạt (đơn vị: mét) tại thời điểm t; tìm các hàm vận tốc và gia tốc. Bài 1.26 trang 40 Toán 12 Tập 1

Bài 1.27 trang 41 Toán 12 Tập 1
Giả sử chi phí (tính bằng trăm nghìn đồng) để sản xuất x đơn vị hàng hóa nào đó, tìm hàm chi phí biên. Bài 1.27 trang 41 Toán 12 Tập 1

Bài 1.28 trang 41 Toán 12 Tập 1
Người quản lí của một khu chung cư có 100 căn hộ cho thuê nhận thấy rằng tất cả các căn hộ sẽ có người thuê nếu giá thuê một căn hộ là 8 triệu đồng một tháng. Bài 1.28 trang 41 Toán 12 Tập 1

Bài 1.29 trang 41 Toán 12 Tập 1
Giả sử hàm cầu đối với một loại hàng hóa trong đó p là giá bán (nghìn đồng) của mỗi đơn vị sản phẩm và x là số lượng đơn vị sản phẩm đã bán. Bài 1.29 trang 41 Toán 12 Tập 1

Mở đầu trang 33 Toán 12 Tập 1
Một đội bóng đá thi đấu trong một sân vận động có sức chứa 55 000 khán giả. Với giá mỗi vé là 100 nghìn đồng, số khán giả trung bình là 27 000 người. Hỏi ban tổ chức nên đặt giá vé là bao nhiêu để doanh thu từ tiền bán vé là lớn nhất?

Luyện tập 1 trang 36 Toán 12 Tập 1
Khi máu di chuyển từ tim qua các động mạch chính rồi đến các mao mạch và quay trở lại qua các tĩnh mạch, huyết áp tâm thu (tức là áp lực của máu lên động mạch khi tim co bóp) liên tục giảm xuống. Luyện tập 1 trang 36 Toán 12 Tập 1

Luyện tập 2 trang 38 Toán 12 Tập 1
Anh An chèo thuyền từ điểm A trên bờ một con sông thẳng rộng 3 km và muốn đến điểm B ở bờ đối diện cách 8 km về phía hạ lưu càng nhanh càng tốt (H.1.35). Luyện tập 2 trang 38 Toán 12 Tập 1

Vận dụng trang 40 Toán 12 Tập 1
Một nhà sản xuất trung bình bán được 1000 ti vi màn hình phẳng mỗi tuần với giá 14 triệu đồng một chiếc. Một cuộc khảo sát thị trường chỉ ra rằng nếu cứ giảm giá bán 500 nghìn đồng, số lượng ti vi bán ra sẽ tăng thêm khoảng 100 ti vi mỗi tuần.
Giải bài tập Bài tập cuối chương 1

Bài 1.30 trang 42 Toán 12 Tập 1
Cho hàm số y = f(x) có đạo hàm trên khoảng (a; b); phát biểu nào dưới đây là đúng. Bài 1.30 trang 42 Toán 12 Tập 1

Bài 1.31 trang 42 Toán 12 Tập 1
Hàm số nào sau đây nghịch biến trên ℝ. Bài 1.31 trang 42 Toán 12 Tập 1
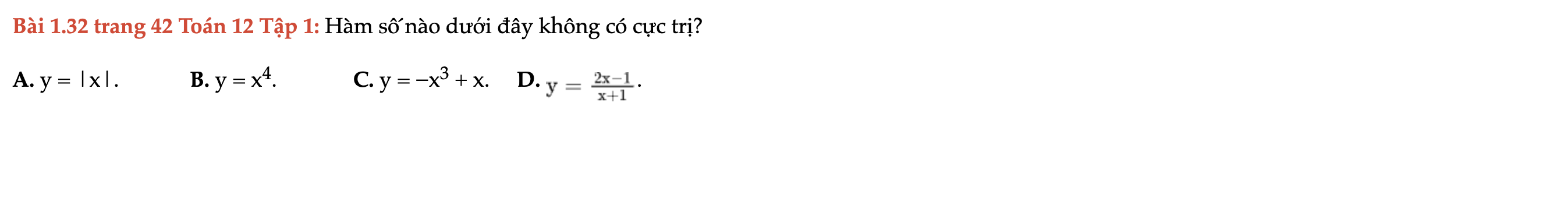
Bài 1.32 trang 42 Toán 12 Tập 1
Hàm số nào dưới đây không có cực trị. Bài 1.32 trang 42 Toán 12 Tập 1
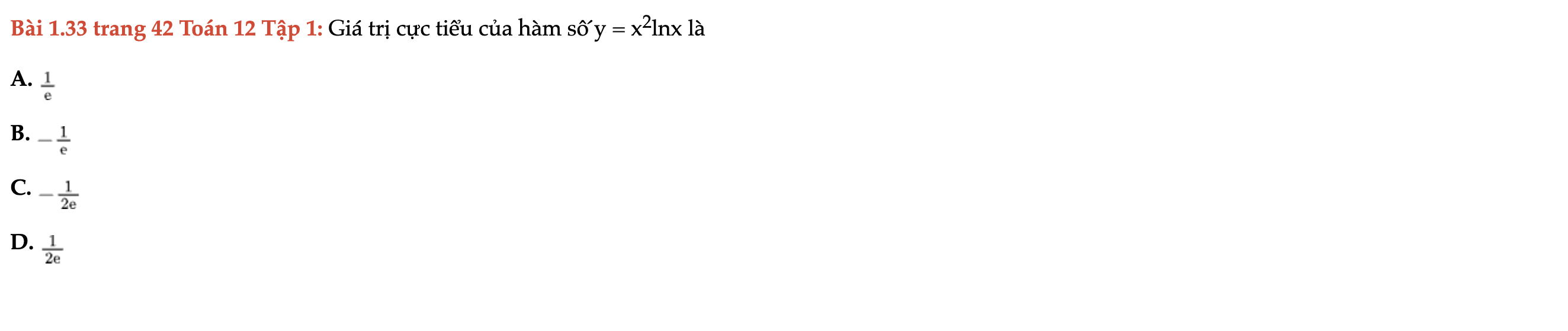
Bài 1.33 trang 42 Toán 12 Tập 1
Giá trị cực tiểu của hàm số. Bài 1.33 trang 42 Toán 12 Tập 1

Bài 1.34 trang 42 Toán 12 Tập 1
Giá trị lớn nhất của hàm số. Bài 1.34 trang 42 Toán 12 Tập 1
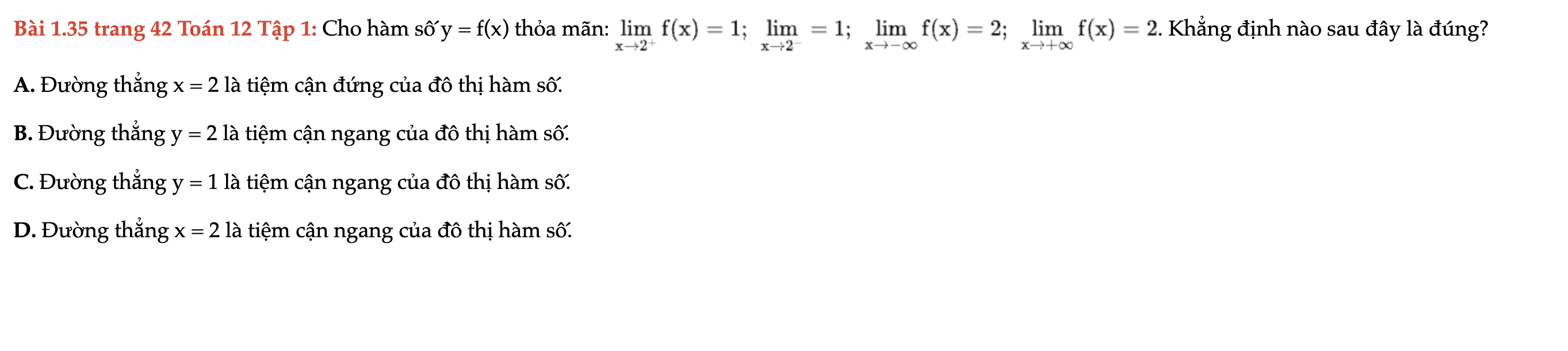
Bài 1.35 trang 42 Toán 12 Tập 1
Khẳng định nào sau đây là đúng. Bài 1.35 trang 42 Toán 12 Tập 1
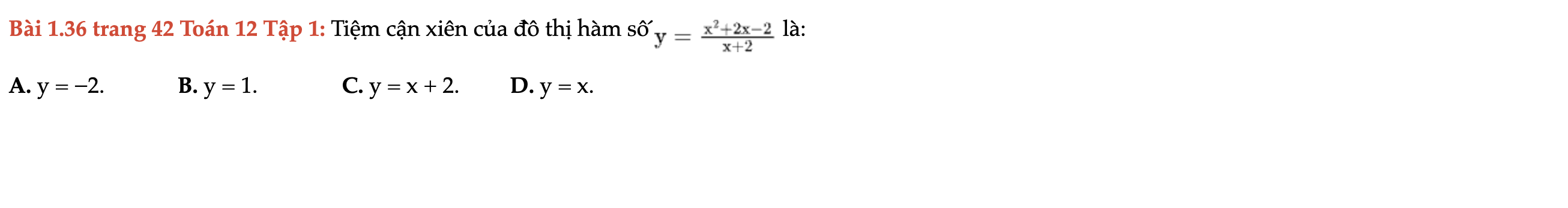
Bài 1.36 trang 42 Toán 12 Tập 1
Tiệm cận xiên của đồ thị hàm số. Bài 1.36 trang 42 Toán 12 Tập 1
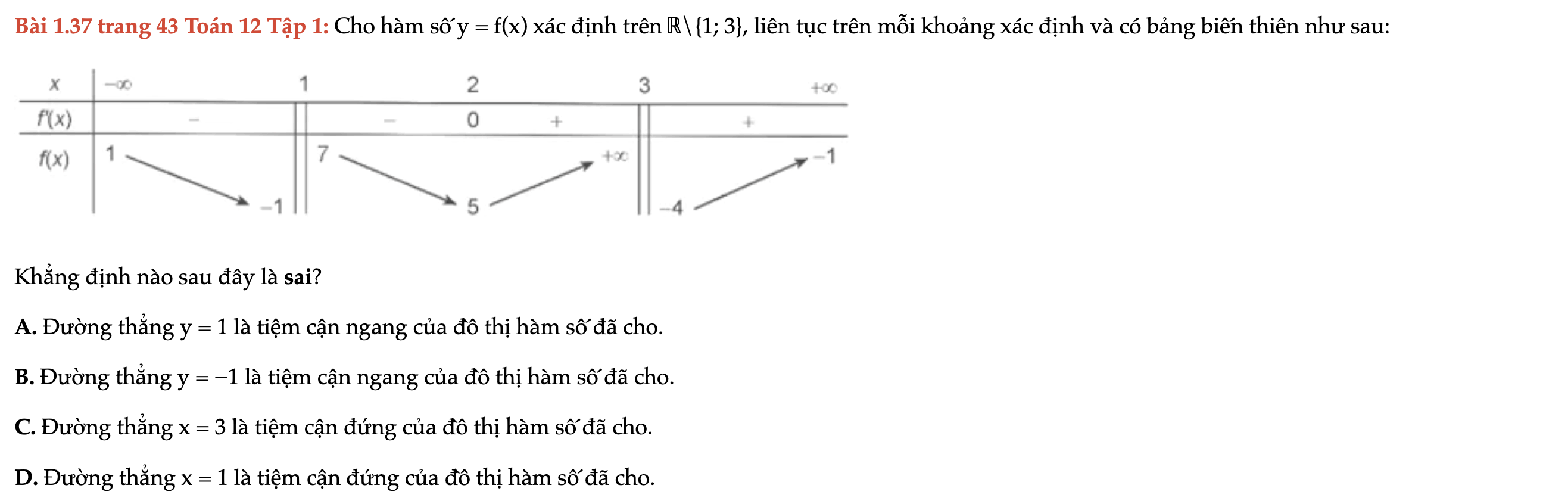
Bài 1.37 trang 43 Toán 12 Tập 1
Cho hàm số y = f(x) xác định trên ℝ\{1; 3}, liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau; khẳng định nào sau đây là sai. Bài 1.37 trang 43 Toán 12 Tập 1

Bài 1.38 trang 43 Toán 12 Tập 1
Đồ thị trong Hình 1.37 là đồ thị của hàm số. Bài 1.38 trang 43 Toán 12 Tập 1

Bài 1.39 trang 43 Toán 12 Tập 1
Đồ thị trong Hình 1.38 là đồ thị của hàm số. Bài 1.39 trang 43 Toán 12 Tập 1

Bài 1.40 trang 43 Toán 12 Tập 1
Xét chiều biến thiên và tìm các cực trị (nếu có) của các hàm số sau. Bài 1.40 trang 43 Toán 12 Tập 1

Bài 1.41 trang 44 Toán 12 Tập 1
Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của các hàm số sau. Bài 1.41 trang 44 Toán 12 Tập 1

Bài 1.42 trang 44 Toán 12 Tập 1
Tìm các tiệm cận của mỗi đồ thị hàm số sau. Bài 1.42 trang 44 Toán 12 Tập 1

Bài 1.43 trang 44 Toán 12 Tập 1
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau. Bài 1.43 trang 44 Toán 12 Tập 1

Bài 1.44 trang 44 Toán 12 Tập 1
Xét một thấu kính hội tụ có tiêu cự f (H.1.39). Khoảng cách p từ vật đến thấu kính liên hệ với khoảng cách q từ ảnh đến thấu kính bởi hệ thức. Bài 1.44 trang 44 Toán 12 Tập 1

Bài 1.45 trang 44 Toán 12 Tập 1
Dân số của một quốc gia sau t (năm) kể từ năm 2023 được tính bằng triệu người, 0 ≤ t ≤ 50). Bài 1.45 trang 44 Toán 12 Tập 1

Bài 1.46 trang 44 Toán 12 Tập 1
Bài 1.46 trang 44 Toán 12 Tập 1