Giải bài tập Vận dụng 2 trang 22 Toán 12 Tập 1 | SGK Toán 12 - Kết nối tri thức
Hướng dẫn giải chi tiết từng bước bài tập Vận dụng 2 trang 22 Toán 12 Tập 1. Bài 3. Đường tiệm cận của đồ thị hàm số.. SGK Toán 12 - Kết nối tri thức
Đề bài:
Để loại bỏ p% một loài tảo độc khỏi một hồ nước, người ta ước tính chi phí bỏ ra là 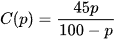 (triệu đồng), với
(triệu đồng), với  . Tìm tiệm cận đứng của đồ thị hàm số C(p) và nêu ý nghĩa thực tiễn của đường tiệm cận này.
. Tìm tiệm cận đứng của đồ thị hàm số C(p) và nêu ý nghĩa thực tiễn của đường tiệm cận này.
Đáp án và cách giải chi tiết:
Ta có 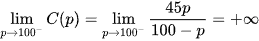
Vậy p = 100 là đường tiệm cận đứng của đồ thị hàm số C(P).
Đường tiệm cận đứng cho ta biết rằng không thể loại bỏ 100% tảo độc ra khỏi hồ nước.
Nguồn: loigiaitoan.com
Tổng số đánh giá:
Xếp hạng: / 5 sao
Bài tập liên quan:
Bài 1.16 trang 25 Toán 12 Tập 1
Bài 1.16 trang 25 Toán 12 Tập 1: Hình 1.26 là đồ thị của hàm số . Sử dụng đồ thị này, hãy:
a) Viết kết quả của các giới hạn sau:
b) Chỉ ra các tiệm cận của đồ thị hàm số đã cho.

Bài 1.17 trang 25 Toán 12 Tập 1
Bài 1.17 trang 25 Toán 12 Tập 1: Đường thẳng x = 1 có phải là tiệm cận đứng của đồ thị hàm số không?
Bài 1.18 trang 25 Toán 12 Tập 1
Bài 1.18 trang 25 Toán 12 Tập 1: Tìm các tiệm cận của đồ thị các hàm số sau:
a)
b)
Bài 1.19 trang 25 Toán 12 Tập 1
Bài 1.19 trang 25 Toán 12 Tập 1: Một công ty sản xuất đồ gia dụng ước tính chi phí để sản xuất x (sản phẩm) là C(x) = 2x + 50 (triệu đồng). Khi đó là chi phí sản xuất trung bình cho mỗi sản phẩm. Chứng tỏ rằng hàm số f(x) giảm và . Tính chất này nói lên điều gì?
Bài 1.20 trang 25 Toán 12 Tập 1
Bài 1.20 trang 25 Toán 12 Tập 1: Một mảnh vườn hình chữ nhật có diện tích bằng 144 m2. Biết độ dài một cạnh của mảnh vườn là x (m).
a) Viết biểu thức tính chu vi P(x) mét của mảnh vườn.
b) Tìm các tiệm cận của đồ thị hàm số P(x).
Mở đầu trang 20 Toán 12 Tập 1
Giả sử khối lượng còn lại của một chất phóng xạ (gam) sau t ngày phân rã được cho bởi hàm số  . Khối lượng m(t) thay đổi ra sao khi
. Khối lượng m(t) thay đổi ra sao khi  ? Điều này thể hiện trên Hình 1.18 như thế nào?
? Điều này thể hiện trên Hình 1.18 như thế nào?

HĐ1 trang 20 Toán 12 Tập
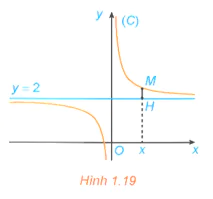
Cho hàm số 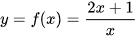 có đồ thị (C). Với x > 0, xét điểm M(x; f(x)) thuộc (C). Gọi H là hình chiếu vuông góc của M trên đường thẳng y = 2 (H.1.19).
có đồ thị (C). Với x > 0, xét điểm M(x; f(x)) thuộc (C). Gọi H là hình chiếu vuông góc của M trên đường thẳng y = 2 (H.1.19).
a) Tính khoảng cách MH.
b) Có nhận xét gì về khoảng cách MH khi 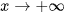 .
.
HĐ2 trang 21 Toán 12 Tập 1
Cho hàm số 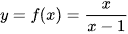 có đồ thị (C). Với x > 1, xét điểm M(x; f(x)) thuộc (C). Gọi H là hình chiếu vuông góc của M trên đường thẳng x = 1 (H.1.22).
có đồ thị (C). Với x > 1, xét điểm M(x; f(x)) thuộc (C). Gọi H là hình chiếu vuông góc của M trên đường thẳng x = 1 (H.1.22).
a) Tính khoảng cách MH.
b) Khi M thay đổi trên (C) sao cho khoảng cách MH dần đến 0, có nhận xét gì về tung độ của điểm M.

Luyện tập 2 trang 22 Toán 12 Tập 1
Tìm các tiệm cận ngang và tiệm cận đứng của đồ thị hàm số  .
.
HĐ3 trang 23 Toán 12 Tập 1
Cho hàm số  có đồ thị (C) và đường thẳng
có đồ thị (C) và đường thẳng  như hình 1.24.
như hình 1.24.
a) Với x > −1, xét điểm M(x; f(x)) thuộc (C). Gọi H là hình chiếu vuông góc của M trên đường thẳng  . Có nhận xét gì về khoảng cách MH khi
. Có nhận xét gì về khoảng cách MH khi  ?
?
b) Chứng tỏ rằng  . Tính chất này thể hiện trên Hình 1.24 như thế nào?
. Tính chất này thể hiện trên Hình 1.24 như thế nào?

Luyện tập 3 trang 24 Toán 12 Tập 1
Tìm các tiệm cận đứng và tiệm cận xiên của đồ thị hàm số  .
.
 .
.