Giải bài tập Bài 1.19 trang 25 Toán 12 Tập 1 | SGK Toán 12 - Kết nối tri thức
Hướng dẫn giải chi tiết từng bước bài tập Bài 1.19 trang 25 Toán 12 Tập 1. Bài 3. Đường tiệm cận của đồ thị hàm số.. SGK Toán 12 - Kết nối tri thức
Đề bài:
Bài 1.19 trang 25 Toán 12 Tập 1: Một công ty sản xuất đồ gia dụng ước tính chi phí để sản xuất x (sản phẩm) là C(x) = 2x + 50 (triệu đồng). Khi đó là chi phí sản xuất trung bình cho mỗi sản phẩm. Chứng tỏ rằng hàm số f(x) giảm và . Tính chất này nói lên điều gì?
Đáp án và cách giải chi tiết:
Có
Có . Do đó hàm số f(x) giảm.
Có
Tính chất này nói lên rằng chi phí sản xuất trung bình cho mỗi sản phẩm sẽ giảm khi số lượng sản phẩm được sản xuất tăng lên và giới hạn của chi phí trung bình là 2 triệu đồng khi số lượng sản phẩm tiến gần đến vô cùng. Điều này có thể hiểu là khi sản xuất nhiều sản phẩm hơn, chi phí trung bình cho mỗi sản phẩm sẽ giảm và tiến gần đến một giá trị ổn định.
Nguồn: loigiaitoan.com
Tổng số đánh giá:
Xếp hạng: / 5 sao
Bài tập liên quan:
Bài 1.16 trang 25 Toán 12 Tập 1
Bài 1.16 trang 25 Toán 12 Tập 1: Hình 1.26 là đồ thị của hàm số . Sử dụng đồ thị này, hãy:
a) Viết kết quả của các giới hạn sau:
b) Chỉ ra các tiệm cận của đồ thị hàm số đã cho.

Bài 1.17 trang 25 Toán 12 Tập 1
Bài 1.17 trang 25 Toán 12 Tập 1: Đường thẳng x = 1 có phải là tiệm cận đứng của đồ thị hàm số không?
Bài 1.18 trang 25 Toán 12 Tập 1
Bài 1.18 trang 25 Toán 12 Tập 1: Tìm các tiệm cận của đồ thị các hàm số sau:
a)
b)
Bài 1.20 trang 25 Toán 12 Tập 1
Bài 1.20 trang 25 Toán 12 Tập 1: Một mảnh vườn hình chữ nhật có diện tích bằng 144 m2. Biết độ dài một cạnh của mảnh vườn là x (m).
a) Viết biểu thức tính chu vi P(x) mét của mảnh vườn.
b) Tìm các tiệm cận của đồ thị hàm số P(x).
Mở đầu trang 20 Toán 12 Tập 1
Giả sử khối lượng còn lại của một chất phóng xạ (gam) sau t ngày phân rã được cho bởi hàm số  . Khối lượng m(t) thay đổi ra sao khi
. Khối lượng m(t) thay đổi ra sao khi  ? Điều này thể hiện trên Hình 1.18 như thế nào?
? Điều này thể hiện trên Hình 1.18 như thế nào?

HĐ1 trang 20 Toán 12 Tập
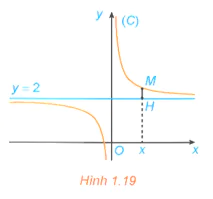
Cho hàm số 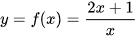 có đồ thị (C). Với x > 0, xét điểm M(x; f(x)) thuộc (C). Gọi H là hình chiếu vuông góc của M trên đường thẳng y = 2 (H.1.19).
có đồ thị (C). Với x > 0, xét điểm M(x; f(x)) thuộc (C). Gọi H là hình chiếu vuông góc của M trên đường thẳng y = 2 (H.1.19).
a) Tính khoảng cách MH.
b) Có nhận xét gì về khoảng cách MH khi 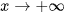 .
.
HĐ2 trang 21 Toán 12 Tập 1
Cho hàm số 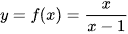 có đồ thị (C). Với x > 1, xét điểm M(x; f(x)) thuộc (C). Gọi H là hình chiếu vuông góc của M trên đường thẳng x = 1 (H.1.22).
có đồ thị (C). Với x > 1, xét điểm M(x; f(x)) thuộc (C). Gọi H là hình chiếu vuông góc của M trên đường thẳng x = 1 (H.1.22).
a) Tính khoảng cách MH.
b) Khi M thay đổi trên (C) sao cho khoảng cách MH dần đến 0, có nhận xét gì về tung độ của điểm M.

Luyện tập 2 trang 22 Toán 12 Tập 1
Tìm các tiệm cận ngang và tiệm cận đứng của đồ thị hàm số  .
.
Vận dụng 2 trang 22 Toán 12 Tập 1
Để loại bỏ p% một loài tảo độc khỏi một hồ nước, người ta ước tính chi phí bỏ ra là 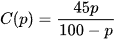 (triệu đồng), với
(triệu đồng), với  . Tìm tiệm cận đứng của đồ thị hàm số C(p) và nêu ý nghĩa thực tiễn của đường tiệm cận này.
. Tìm tiệm cận đứng của đồ thị hàm số C(p) và nêu ý nghĩa thực tiễn của đường tiệm cận này.
HĐ3 trang 23 Toán 12 Tập 1
Cho hàm số  có đồ thị (C) và đường thẳng
có đồ thị (C) và đường thẳng  như hình 1.24.
như hình 1.24.
a) Với x > −1, xét điểm M(x; f(x)) thuộc (C). Gọi H là hình chiếu vuông góc của M trên đường thẳng  . Có nhận xét gì về khoảng cách MH khi
. Có nhận xét gì về khoảng cách MH khi  ?
?
b) Chứng tỏ rằng  . Tính chất này thể hiện trên Hình 1.24 như thế nào?
. Tính chất này thể hiện trên Hình 1.24 như thế nào?

Luyện tập 3 trang 24 Toán 12 Tập 1
Tìm các tiệm cận đứng và tiệm cận xiên của đồ thị hàm số  .
.
 .
.