Giải bài tập Toán 12 Chương 4. Nguyên hàm và Tích phân. | Kết Nối Tri Thức
Chương 4. Nguyên hàm và Tích phân. Khái niệm và tính chất cơ bản của Nguyên hàm, tích phân. Xác định nguyên hàm hàm số cơ bản, tính được tích phân cơ bản. Ứng dụng tích phân để tính diện tích hình phẳng, thể tích và bài toán thực tế.
Giải bài tập Bài 11. Nguyên hàm.

Bài 4.1 trang 11 Toán 12 Tập 2
Trong mỗi trường hợp sau, hàm số F(x) có là một nguyên hàm của hàm số f(x) trên khoảng tương ứng không? Vì sao? Bài 4.1 trang 11 Toán 12 Tập 2

Bài 4.2 trang 11 Toán 12 Tập 2
Tìm nguyên hàm của các hàm số sau. Bài 4.2 trang 11 Toán 12 Tập 2

Bài 4.3 trang 11 Toán 12 Tập 2
Tìm nguyên hàm. Bài 4.3 trang 11 Toán 12 Tập 2

Bài 4.4 trang 11 Toán 12 Tập 2
Tìm nguyên hàm. Bài 4.4 trang 11 Toán 12 Tập 2
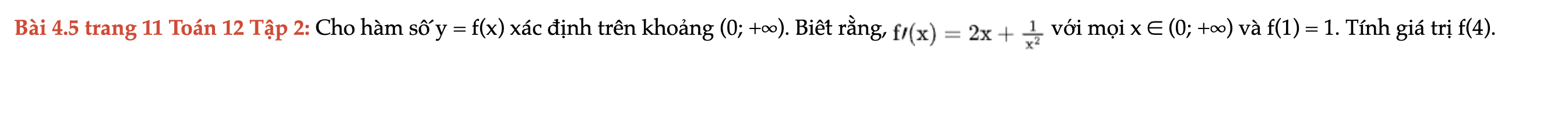
Bài 4.5 trang 11 Toán 12 Tập 2
Cho hàm số y = f(x) xác định trên khoảng (0; +∞) biết f'(x) và f(1)=1; tính f(4). Bài 4.5 trang 11 Toán 12 Tập 2

Bài 4.6 trang 11 Toán 12 Tập 2
Cho hàm số y = f(x) có đồ thị là (C). Xét điểm M(x; f(x)) thay đổi trên (C). Biết rằng, hệ số góc của tiếp tuyến của đồ thị (C) tại M là kM = (x-1)^2 và điểm M trùng với gốc tọa độ khi nó nằm trên trục tung. Tìm f(x). Bài 4.6 trang 11 Toán 12 Tập 2

Bài 4.7 trang 11 Toán 12 Tập 2
Một viên đạn được bắn thẳng đứng lên trên từ mặt đất. Giả sử tại thời điểm t giây (coi t=0 là thời điểm viên đạn được bắn lên), vận tốc của nó được cho bởi v(t) = 160 – 9,8t (m/s). Tìm độ cao của viên đạn (tính từ mặt đất). Bài 4.7 trang 11 Toán 12 Tập 2

Mở đầu trang 4 Toán 12 Tập 2
Một máy bay di chuyển ra đến đường băng và bắt đầu chạy đà để cất cánh. Giả sử vận tốc của máy bay khi chạy đà được cho bởi v(t) = 5 + 3t (m/s). Mở đầu trang 4 Toán 12 Tập 2
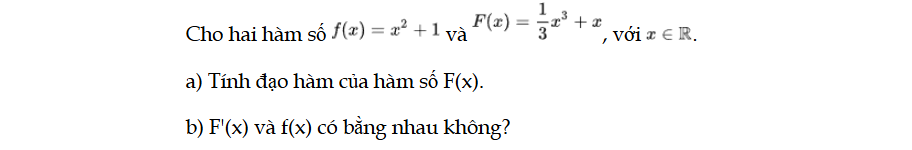
HĐ1 trang 4 Toán 12 Tập 2
Cho hai hàm số f(x) và F(x). a) Tính đạo hàm của hàm số F(x). b) F'(x) và f(x) có bằng nhau không? HĐ1 trang 4 Toán 12 Tập 2
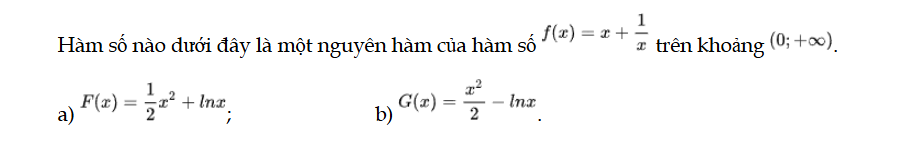
Luyện tập 1 trang 5 Toán 12 Tập 2
Hàm số nào dưới đây là một nguyên hàm của hàm số f(x). Luyện tập 1 trang 5 Toán 12 Tập 2

HĐ2 trang 5 Toán 12 Tập 2
HĐ2 trang 5 Toán 12 Tập 2
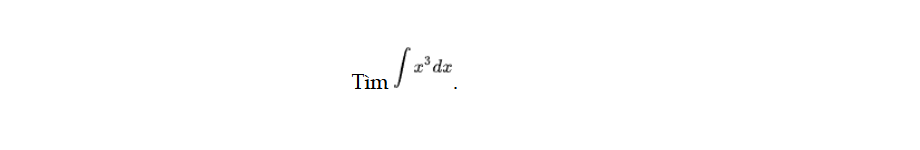
Luyện tập 2 trang 6 Toán 12 Tập 2
Tìm nguyên hàm. Luyện tập 2 trang 6 Toán 12 Tập 2

HĐ3 trang 6 Toán 12 Tập 2
Cho f(x) là hàm số liên tục trên K, k là một hằng số khác 0. Giả sử F(x) là một nguyên hàm của f(x) trên K. HĐ3 trang 6 Toán 12 Tập 2

Luyện tập 3 trang 7 Toán 12 Tập 2
Cho hàm số f(x), thực hiện các yêu cầu đề bài. Luyện tập 3 trang 7 Toán 12 Tập 2

HĐ4 trang 7 Toán 12 Tập 2
Cho f(x) và g(x) là hai hàm số liên tục trên K. Giả sử F(x) là một nguyên hàm của f(x), G(x) là một nguyên hàm của g(x) trên K. HĐ4 trang 7 Toán 12 Tập 2
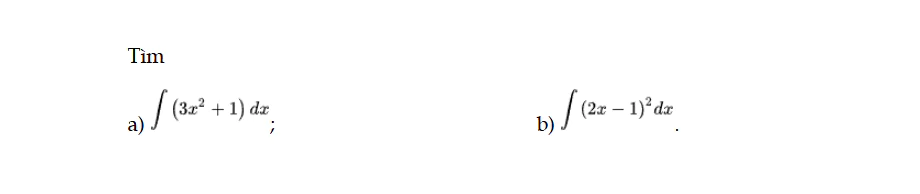
Luyện tập 4 trang 7 Toán 12 Tập 2
Tìm các nguyên hàm sau. Luyện tập 4 trang 7 Toán 12 Tập 2

Vận dụng trang 8 Toán 12 Tập 2
Doanh thu bán hàng của một công ty khi bán một loại sản phẩn là số tiền R(x) (triệu đồng) thu được khi x đơn vị sản phẩm được bán ra. Tốc độ biến động (thay đổi) của doanh thu khi x đơn vị sản phẩm đã được bán là hàm số MR(x) = R'(x).
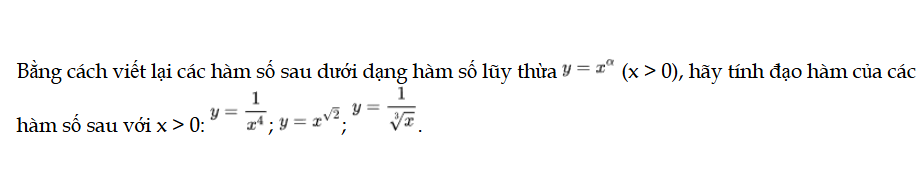
Câu hỏi trang 8 Toán 12 Tập 2
Bằng cách viết lại các hàm số sau dưới dạng hàm số lũy thừa, hãy tính đạo hàm của các hàm số sau với x > 0. Câu hỏi trang 8 Toán 12 Tập 2
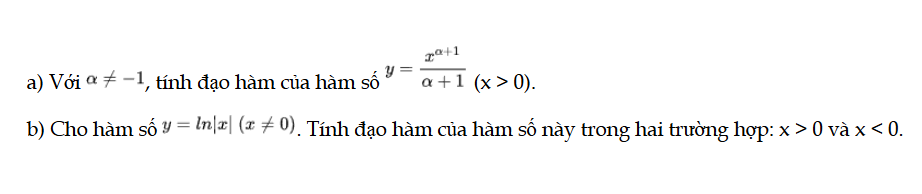
HĐ5 trang 8 Toán 12 Tập 2
HĐ5 trang 8 Toán 12 Tập 2
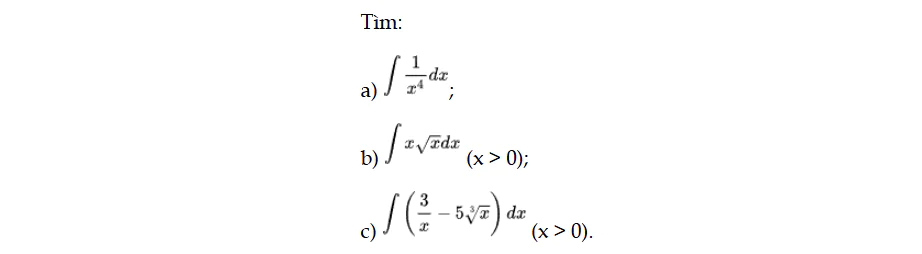
Luyện tập 5 trang 9 Toán 12 Tập 2
Tìm. Luyện tập 5 trang 9 Toán 12 Tập 2
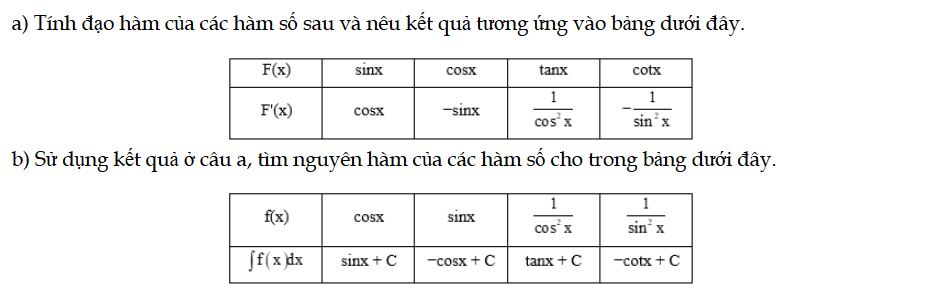
HĐ6 trang 9 Toán 12 Tập 2
a) Tính đạo hàm của các hàm số sau và nêu kết quả tương ứng vào bảng dưới đây. b) Sử dụng kết quả ở câu a, tìm nguyên hàm của các hàm số cho trong bảng dưới đây. HĐ6 trang 9 Toán 12 Tập 2
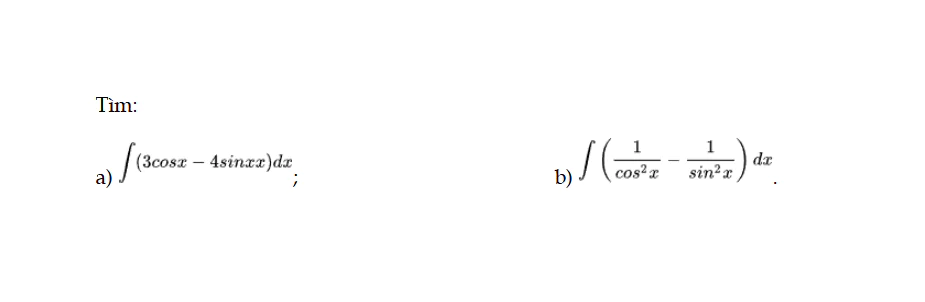
Luyện tập 6 trang 9 Toán 12 Tập 2
Tìm các đạo hàm sau. Luyện tập 6 trang 9 Toán 12 Tập 2

HĐ7 trang 10 Toán 12 Tập 2
a) Tính đạo hàm của các hàm số sau và nêu kết quả tương ứng vào bảng dưới đây. b) Sử dụng kết quả ở câu a, tìm nguyên hàm của các hàm số cho trong bảng dưới đây. HĐ7 trang 10 Toán 12 Tập 2
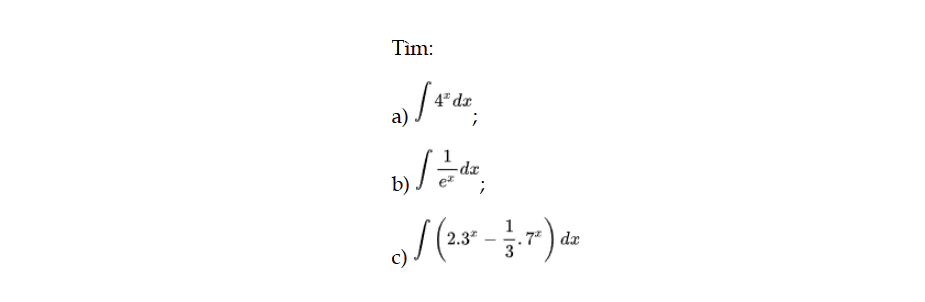
Luyện tập 7 trang 10 Toán 12 Tập 2
Tìm. Luyện tập 7 trang 10 Toán 12 Tập 2
Giải bài tập Bài 12. Tích phân.

Bài 4.8 trang 18 Toán 12 Tập 2
Sử dụng ý nghĩa hình học của tích phân để tính các câu sau. Bài 4.8 trang 18 Toán 12 Tập 2
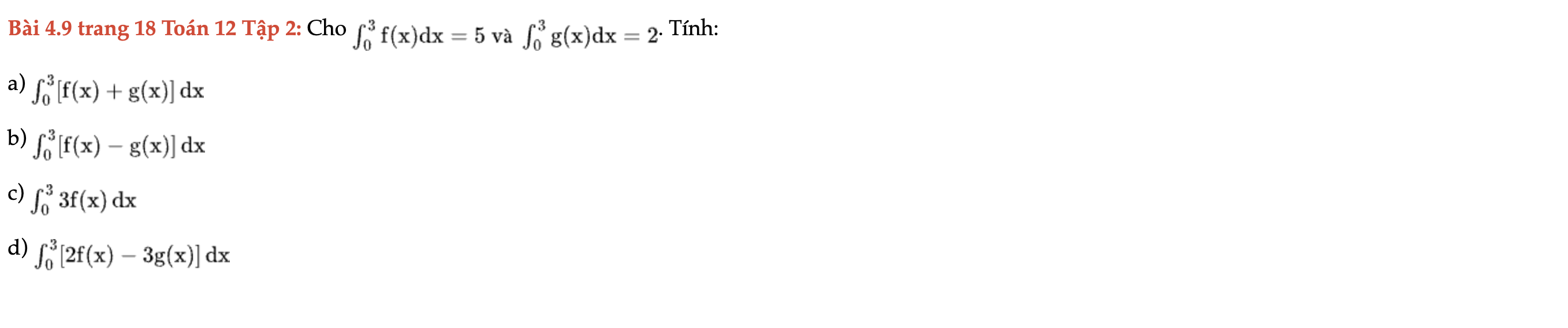
Bài 4.9 trang 18 Toán 12 Tập 2
Cho giá trị các tích phân sau, tính các tích phân dưới đây. Bài 4.9 trang 18 Toán 12 Tập 2

Bài 4.10 trang 18 Toán 12 Tập 2
Tính các tích phân sau. Bài 4.10 trang 18 Toán 12 Tập 2

Bài 4.11 trang 18 Toán 12 Tập 2
Một vật chuyển động dọc theo một đường thẳng sao cho vận tốc của nó tại thời điểm t (giây); tìm độ dịch chuyển của vật trong khoảng thời gian 1 ≤ t ≤ 4. Bài 4.11 trang 18 Toán 12 Tập 2

Bài 4.12 trang 18 Toán 12 Tập 2
Giả sử lợi nhuận biên (tính bằng triệu đồng) của một sản phẩm được mô hình hóa bằng công thức P'(x) = −0,0005x + 12,2. Ở đây P(x) là lợi nhuận (tính bằng triệu đồng) khi bán được x đơn vị sản phẩm. Bài 4.12 trang 18 Toán 12 Tập 2

Bài 4.13 trang 18 Toán 12 Tập 2
Giả sử vận tốc v của dòng máu ở khoảng cách r từ tâm của động mạch bán kính R không đổi, tìm vận tốc trung bình (đối với r) của động mạch trong khoảng 0 ≤ r ≤ R. So sánh vận tốc trung bình với vận tốc lớn nhất. Bài 4.13 trang 18 Toán 12 Tập 2

Mở đầu trang 12 Toán 12 Tập 2
Một ô tô đang chạy với vận tốc 20 m/s thì người lái đạp phanh. Sau khi đạp phanh, ô tô chuyển động chậm dần đều với vận tốc v(t) = −40t + 20 (m/s), trong đó t là thời gian tính bằng giây kể từ lúc đạp phanh. Mở đầu trang 12 Toán 12 Tập 2
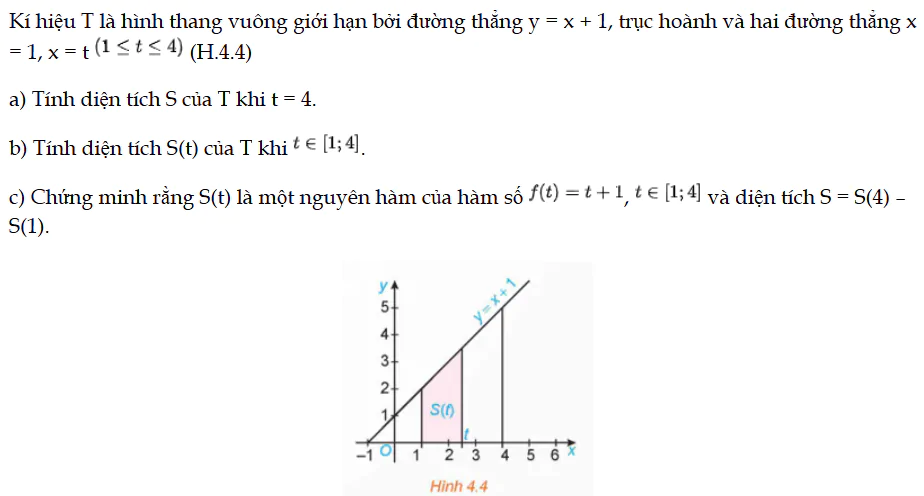
HĐ1 trang 13 Toán 12 Tập 2
Kí hiệu T là hình thang vuông giới hạn bởi đường thẳng y = x + 1, trục hoành và hai đường thẳng x = 1, x = t (H.4.4).

HĐ2 trang 13 Toán 12 Tập 2
Xét hình thang cong giới hạn bởi đồ thị y = x2, trục hoành và hai đường thẳng x = 1, x = 2. Ta muốn tính diện tích S của hình thang cong này. HĐ2 trang 13 Toán 12 Tập 2
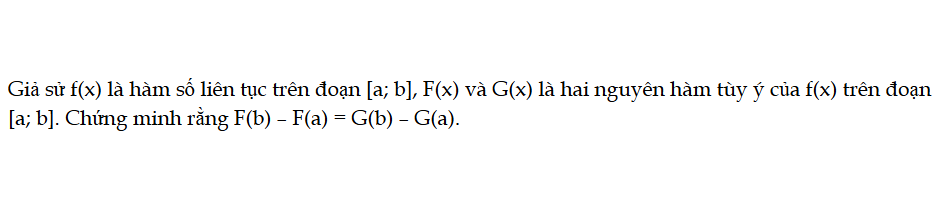
HĐ3 trang 14 Toán 12 Tập 2
Giả sử f(x) là hàm số liên tục trên đoạn [a; b], F(x) và G(x) là hai nguyên hàm tùy ý của f(x) trên đoạn [a; b]. Chứng minh rằng F(b) – F(a) = G(b) – G(a). HĐ3 trang 14 Toán 12 Tập 2
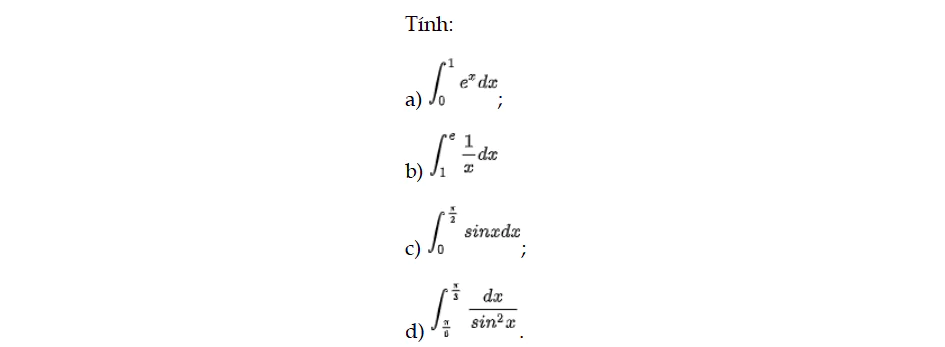
Luyện tập 1 trang 15 Toán 12 Tập 2
Tính các tích phân sau. Luyện tập 1 trang 15 Toán 12 Tập 2
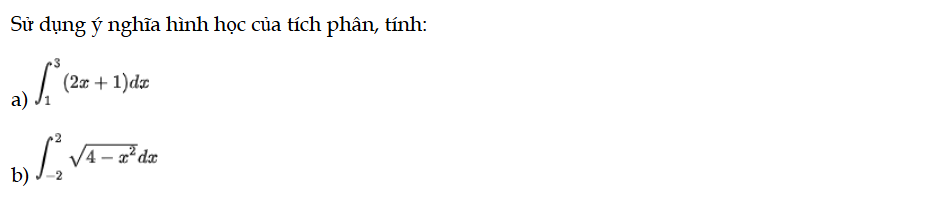
Luyện tập 2 trang 16 Toán 12 Tập 2
Sử dụng ý nghĩa hình học của tích phân, tính: Luyện tập 2 trang 16 Toán 12 Tập 2

Vận dụng 1 trang 16 Toán 12 Tập 2
Giải quyết bài toán ở tình huống mở đầu. Vận dụng 1 trang 16 Toán 12 Tập 2

HĐ4 trang 16 Toán 12 Tập 2
Tính và so sánh: HĐ4 trang 16 Toán 12 Tập 2

Luyện tập 3 trang 17 Toán 12 Tập 2
Tính các tích phân sau. Luyện tập 3 trang 17 Toán 12 Tập 2
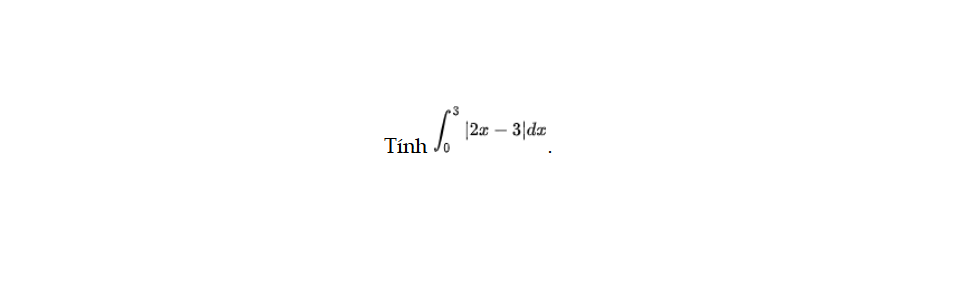
Luyện tập 4 trang 17 Toán 12 Tập 2
Tính tích phân sau. Luyện tập 4 trang 17 Toán 12 Tập 2

Vận dụng 2 trang 17 Toán 12 Tập 2
Giá trị trung bình của hàm số liên tục f(x) trên đoạn [a; b] được định nghĩa là. Giả sử nhiệt độ (tính bằng °C) tại thời điểm t giờ trong khoảng thời gian từ 6 giờ sáng đến 12 giờ trưa ở một địa phương vào một ngày nào đó được mô hình hóa bởi hàm số
Giải bài tập Bài 13. Ứng dụng hình học của tích phân.

Bài 4.14 trang 25 Toán 12 Tập 2
Tính diện tích của hình phẳng được tô màu trong Hình 4.29. Bài 4.14 trang 25 Toán 12 Tập 2

Bài 4.15 trang 25 Toán 12 Tập 2
Tính diện tích của hình phẳng giới hạn bởi các đường sau. Bài 4.15 trang 25 Toán 12 Tập 2

Bài 4.16 trang 25 Toán 12 Tập 2
Các nhà kinh tế sử dụng đường cong Lorenz để minh họa sự phân phối thu nhập trong một quốc gia. Bài 4.16 trang 25 Toán 12 Tập 2

Bài 4.17 trang 26 Toán 12 Tập 2
Tính thể tích của khối tròn xoay sinh ra khi quay hình phẳng giới hạn bởi các đường sau xung quanh trục Ox: y = 2x – x2, y = 0, x = 0, x = 2. Bài 4.17 trang 26 Toán 12 Tập 2

Bài 4.18 trang 26 Toán 12 Tập 2
Khối chỏm cầu có bán kính R và chiều cao h (0 < h ≤ R) sinh ra khi quay hình phẳng giới hạn bởi cung tròn, tính thể tích của khối chỏm cầu này. Bài 4.18 trang 26 Toán 12 Tập 2
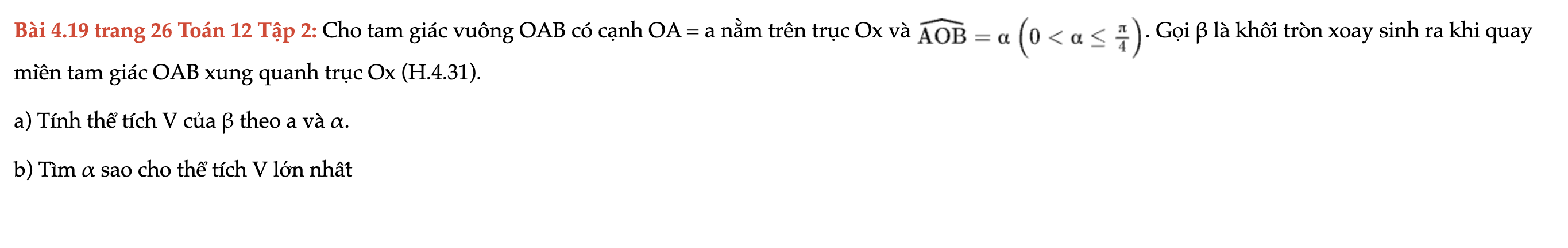
Bài 4.19 trang 26 Toán 12 Tập 2
Cho tam giác vuông OAB có cạnh OA = a nằm trên trục Ox và góc AOB. Gọi β là khối tròn xoay sinh ra khi quay miền tam giác OAB xung quanh trục Ox. Bài 4.19 trang 26 Toán 12 Tập 2
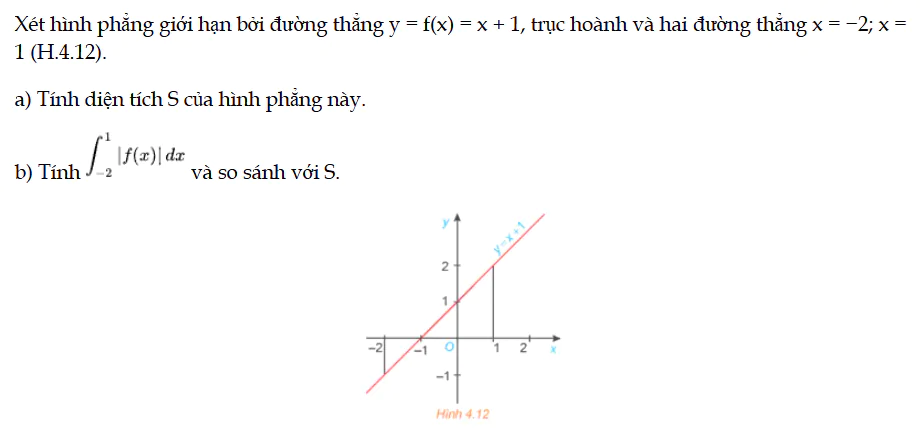
HĐ1 trang 19 Toán 12 Tập 2
Xét hình phẳng giới hạn bởi đường thẳng y = f(x) = x + 1, trục hoành và hai đường thẳng x = −2; x = 1 (H.4.12). HĐ1 trang 19 Toán 12 Tập 2
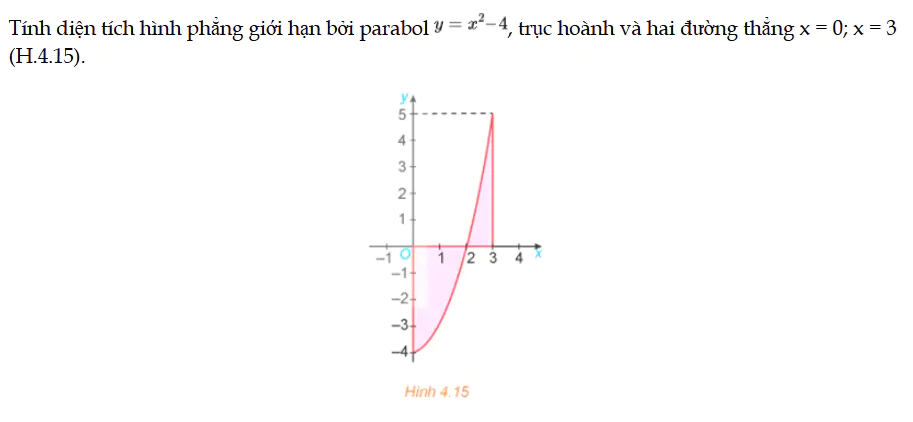
Luyện tập 1 trang 20 Toán 12 Tập 2
Tính diện tích hình phẳng giới hạn bởi parabol, trục hoành và hai đường thẳng x = 0; x = 3 (H.4.15). Luyện tập 1 trang 20 Toán 12 Tập 2
HĐ2 trang 20 Toán 12 Tập 2
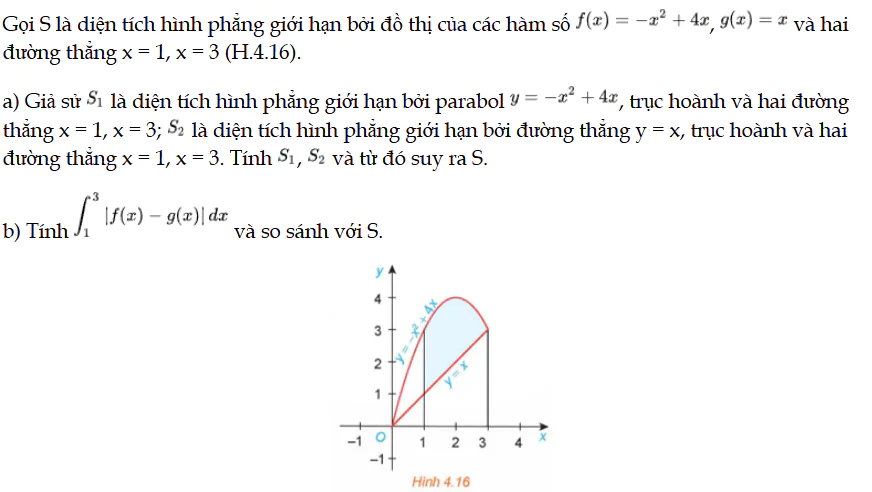
Gọi S là diện tích hình phẳng giới hạn bởi đồ thị của các hàm số f(x), g(x) và hai đường thẳng x = 1, x = 3 (H.4.16). HĐ2 trang 20 Toán 12 Tập 2

Luyện tập 2 trang 21 Toán 12 Tập 2
Tính diện tích hình phẳng giới hạn bởi đồ thị của các hàm số và hai đường thẳng. Luyện tập 2 trang 21 Toán 12 Tập 2

Vận dụng 1 trang 22 Toán 12 Tập 2
Ta biết rằng hàm cầu liên quan đến giá p của một sản phẩm với nhu cầu của người tiêu dùng, hàm cung liên quan đến giá p của sản phẩm với mức độ sẵn sàng cung cấp sản phẩm của nhà sản xuất. Vận dụng 1 trang 22 Toán 12 Tập 2
HĐ3 trang 22 Toán 12 Tập 2
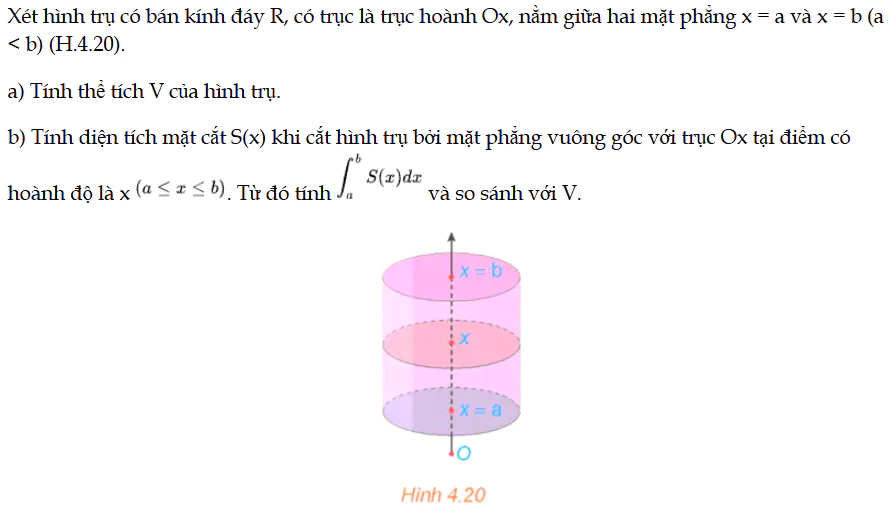
Xét hình trụ có bán kính đáy R, có trục là trục hoành Ox, nằm giữa hai mặt phẳng x = a và x = b (a < b) (H.4.20). HĐ3 trang 22 Toán 12 Tập 2
Vận dụng 2 trang 23 Toán 12 Tập 2
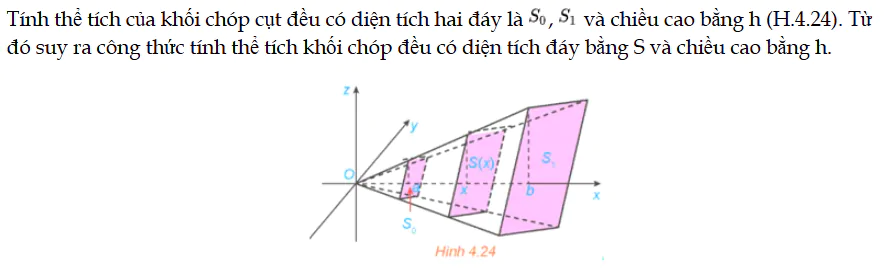
Tính thể tích của khối chóp cụt đều có diện tích hai đáy là S0, S1 và chiều cao bằng h (H.4.24). Từ đó suy ra công thức tính thể tích khối chóp đều có diện tích đáy bằng S và chiều cao bằng h. Vận dụng 2 trang 23 Toán 12 Tập 2

HĐ4 trang 24 Toán 12 Tập 2
Xét hình phẳng giới hạn bởi đồ thị hàm số f(x), trục hoành và hai đường thẳng x = 0, x = 4. Khi quay hình phẳng này xung quanh trục hoành Ox ta được khối nón có đỉnh là gốc O, trục là Ox và đáy là hình tròn bán kính bằng 2 (H.4.25).
Vận dụng 3 trang 25 Toán 12 Tập 2
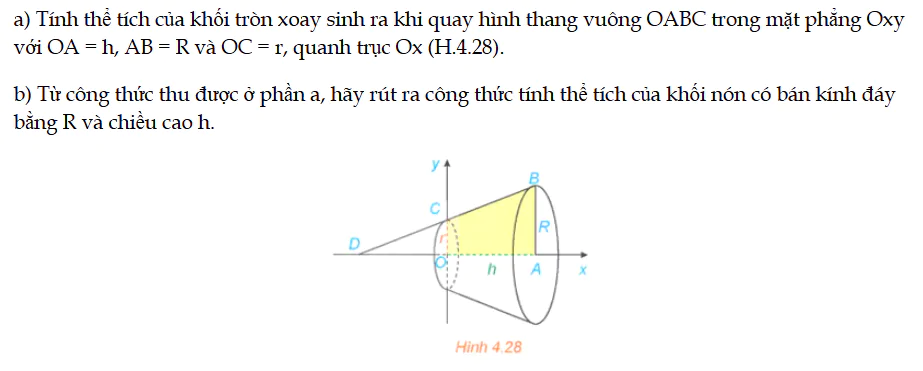
a) Tính thể tích của khối tròn xoay sinh ra khi quay hình thang vuông OABC trong mặt phẳng Oxy với OA = h, AB = R và OC = r, quanh trục Ox (H.4.28). b) Từ công thức thu được ở phần a, hãy rút ra công thức tính thể tích của khối nón có bán kính đáy bằng R
Giải bài tập Bài tập cuối chương 4.
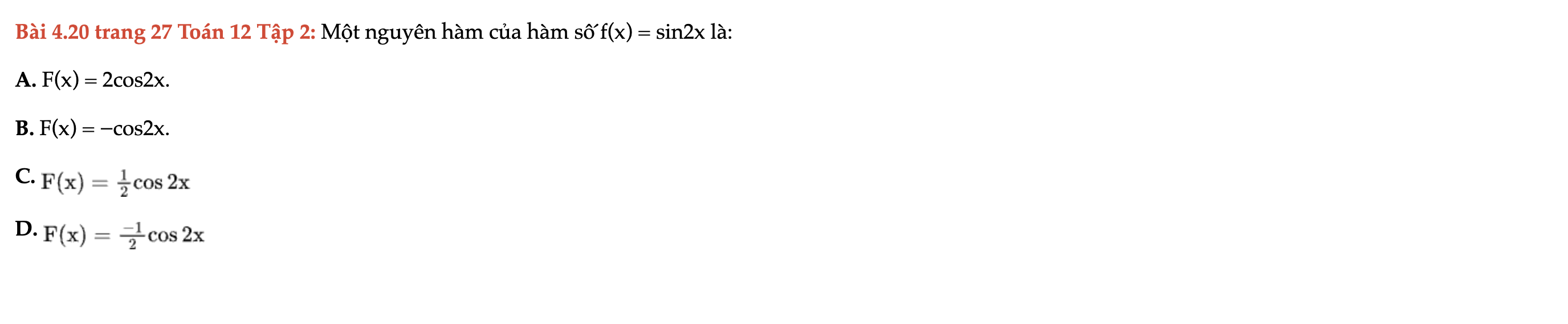
Bài 4.20 trang 27 Toán 12 Tập 2
Bài 4.20 trang 27 Toán 12 Tập 2

Bài 4.21 trang 27 Toán 12 Tập 2
Họ tất cả các nguyên hàm của hàm số 2ex là. Bài 4.21 trang 27 Toán 12 Tập 2

Bài 4.22 trang 27 Toán 12 Tập 2
Nguyên hàm F(x) của hàm số f(x) thỏa mãn F(0) = 4 là. Bài 4.22 trang 27 Toán 12 Tập 2

Bài 4.23 trang 27 Toán 12 Tập 2
Cho hàm số f(x) có đạo hàm f'(x) liên tục trên ℝ, f(1) = 16, khi đó giá trị của f(3) bằng. Bài 4.23 trang 27 Toán 12 Tập 2
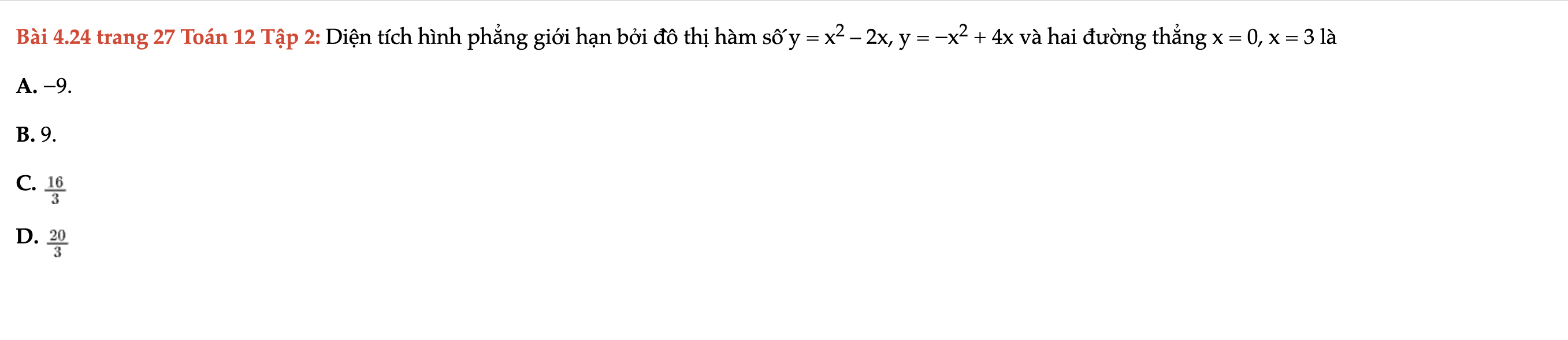
Bài 4.24 trang 27 Toán 12 Tập 2
Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = x2 – 2x, y = −x2 + 4x và hai đường thẳng x = 0, x = 3 là. Bài 4.24 trang 27 Toán 12 Tập 2

Bài 4.25 trang 27 Toán 12 Tập 2
Cho đồ thị hàm số y = f(x) trên đoạn [−2;2] như Hình 4.32. Bài 4.25 trang 27 Toán 12 Tập 2
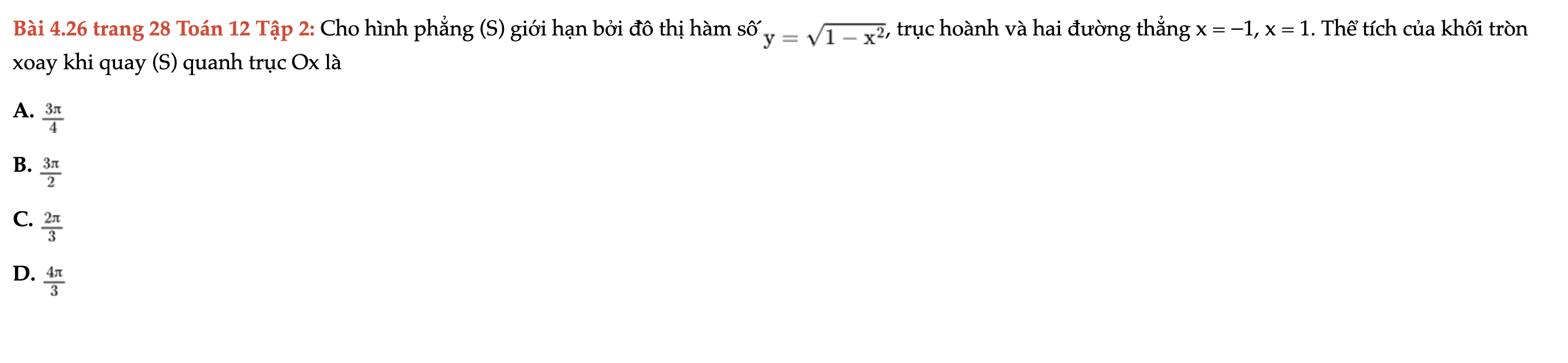
Bài 4.26 trang 28 Toán 12 Tập 2
Cho hình phẳng (S) giới hạn bởi đồ thị hàm số trục hoành và hai đường thẳng x = −1, x = 1. Thể tích của khối tròn xoay khi quay (S) quanh trục Ox là. Bài 4.26 trang 28 Toán 12 Tập 2
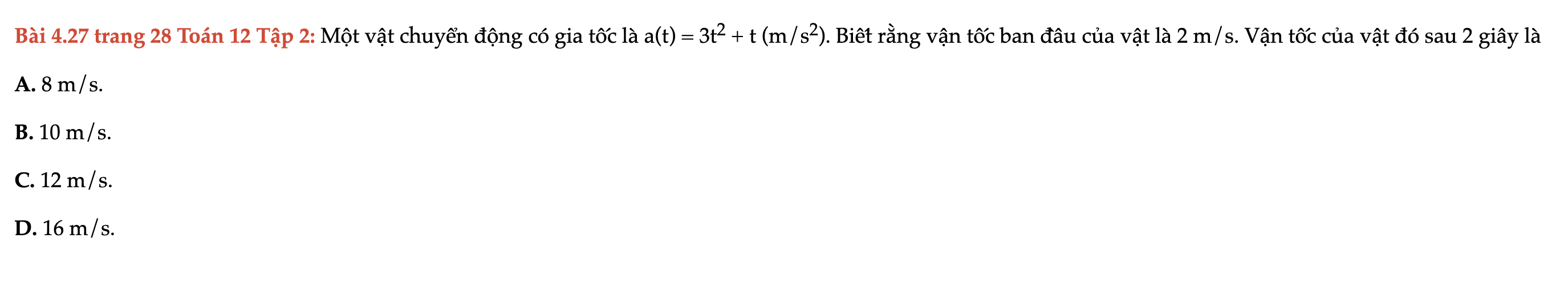
Bài 4.27 trang 28 Toán 12 Tập 2
Một vật chuyển động có gia tốc là a(t), biết rằng vận tốc ban đầu của vật là 2 m/s. Vận tốc của vật đó sau 2 giây là. Bài 4.27 trang 28 Toán 12 Tập 2

Bài 4.28 trang 28 Toán 12 Tập 2
Tìm họ tất cả các nguyên hàm của các hàm số sau. Bài 4.28 trang 28 Toán 12 Tập 2
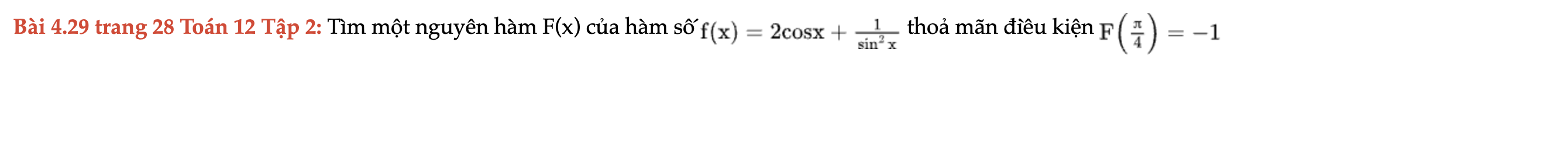
Bài 4.29 trang 28 Toán 12 Tập 2
Tìm một nguyên hàm F(x) của hàm số thoả mãn điều kiện. Bài 4.29 trang 28 Toán 12 Tập 2

Bài 4.30 trang 28 Toán 12 Tập 2
Một viên đạn được bắn lên từ mặt đất theo phương thẳng đứng với vận tốc ban đầu là 30 m/s. Gia tốc trọng trường là 9,8 m/s^2. Tìm vận tốc của viên đạn ở thời điểm 2 giây. Bài 4.30 trang 28 Toán 12 Tập 2

Bài 4.31 trang 28 Toán 12 Tập 2
Cá hồi Thái Bình Dương đến mùa sinh sản thường bơi từ biển ngược dòng vào sông và đến thượng nguồn các dòng sông để đẻ trứng. Bài 4.31 trang 28 Toán 12 Tập 2

Bài 4.32 trang 28 Toán 12 Tập 2
Tính các tích phân sau. Bài 4.32 trang 28 Toán 12 Tập 2

Bài 4.33 trang 28 Toán 12 Tập 2
Tính diện tích hình phẳng giới hạn bởi các đường y = ex, y = x, x = 0 và x = 1. Bài 4.33 trang 28 Toán 12 Tập 2

Bài 4.34 trang 28 Toán 12 Tập 2
Tính thể tích của khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường sau xung quanh trục Ox. Bài 4.34 trang 28 Toán 12 Tập 2

Bài 4.35 trang 28 Toán 12 Tập 2
Nghệ thuật làm gốm có lịch sử phát triển lâu đời và vẫn còn tồn tại cho đến ngày nay. Giả sử một bình gốm có mặt trong của bình là một mặt tròn xoay sinh ra khi cho phần đồ thị của hàm số. Bài 4.35 trang 28 Toán 12 Tập 2