Giải bài tập Toán 10 Chương 7: Phương pháp tọa độ trong mặt phẳng | Kết Nối Tri Thức
Hướng dẫn giải Chương 7: Phương pháp tọa độ trong mặt phẳng
Giải bài tập Bài 19: Phương trình đường thẳng

Bài 7.1 trang 34 Toán 10 Tập 2
Trong mặt phẳng tọa độ, cho vectơ n, vectơ v và A(1;3), B(-2;1). Bài 7.1 trang 34 Toán 10 Tập 2

Bài 7.2 trang 34 Toán 10 Tập 2
Lập phương trình đường thẳng tổng quát của các trục tọa độ. Bài 7.2 trang 34 Toán 10 Tập 2
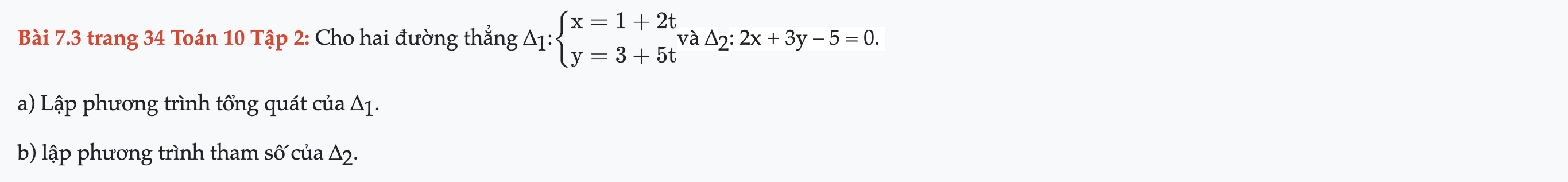
Bài 7.3 trang 34 Toán 10 Tập 2
Cho hai đường thẳng ∆1 và ∆2: 2x + 3y – 5 = 0, lập phương trình tổng quát của ∆1. Bài 7.3 trang 34 Toán 10 Tập 2

Bài 7.4 trang 34 Toán 10 Tập 2
Trong mặt phẳng tọa độ, cho tam giác ABC có A(1; 2), B(3; 0) và C(– 2; – 1). Bài 7.4 trang 34 Toán 10 Tập 2

Bài 7.5 trang 34 Toán 10 Tập 2
(Phương trình đoạn chắn của đường thẳng). Chứng minh rằng, đường thẳng đi qua hai điểm A(a; 0), B(0; b) với ab ≠ 0. Bài 7.5 trang 34 Toán 10 Tập 2

Bài 7.6 trang 34 Toán 10 Tập 2
Theo Google Maps, sân bay Nội Bài có vĩ độ 21,2° Bắc, kinh độ 105,8° Đông, sân bay Đà Nẵng có vĩ độ 16,1° Bắc, kinh độ 108,2° Đông. Bài 7.6 trang 34 Toán 10 Tập 2

HĐ1 trang 31 Toán 10 Tập 2
Cho vectơ n ≠ vectơ 0 và điểm A. Tìm tập hợp những điểm M sao cho vectơ AM vuông góc với vectơ n. HĐ1 trang 31 Toán 10 Tập 2

HĐ2 trang 31 Toán 10 Tập 2
Trong mặt phẳng tọa độ, cho đường thẳng ∆ đi qua điểm A(x0; y0) và có vectơ pháp tuyến n = (a,b). Chứng minh rằng điểm M(x; y) thuộc ∆ khi và chỉ khi a(x – x0) + b(y – y0) = 0. (1) HĐ2 trang 31 Toán 10 Tập 2

Luyện tập 1 trang 32 Toán 10 Tập 2
Trong mặt phẳng tọa độ, cho tam giác có ba đỉnh A(– 1; 5), B(2; 3), C(6; 1). Lập phương trình tổng quát của đường cao kẻ từ A của tam giác ABC. Luyện tập 1 trang 32 Toán 10 Tập 2

Luyện tập 2 trang 32 Toán 10 Tập 2
Hãy chỉ ra một vectơ pháp tuyến của đường thẳng ∆: y = 3x + 4. Luyện tập 2 trang 32 Toán 10 Tập 2

HĐ3 trang 32 Toán 10 Tập 2
Trong Hình 7.2a, nếu một vật thể chuyển động với vectơ vận tốc bằng vectơ v và đi qua A thì nó di chuyển trên đường nào? HĐ3 trang 32 Toán 10 Tập 2

Luyện tập 3 trang 33 Toán 10 Tập 2
Hãy chỉ ra một vectơ chỉ phương của đường thẳng ∆: 2x – y + 1 = 0. Luyện tập 3 trang 33 Toán 10 Tập 2

HĐ4 trang 33 Toán 10 Tập 2
Chuyển động của một vật thể được thể hiện trên mặt phẳng Oxy. Vật thể khởi hành từ A(2; 1) và chuyển động thẳng đều với vectơ vận tốc vectơ v = (3; 4). HĐ4 trang 33 Toán 10 Tập 2

Luyện tập 4 trang 33 Toán 10 Tập 2
Lập phương trình tham số của đường thẳng ∆ đi qua hai điểm M(– 1; 2) và song song với đường thẳng d: 3x – 4y – 1 = 0. Luyện tập 4 trang 33 Toán 10 Tập 2

Luyện tập 5 trang 33 Toán 10 Tập 2
Lập phương trình tham số và phương trình tổng quát của đường thẳng đi qua hai điểm phân biệt A(x1; y1), B(x2; y2) cho trước. Luyện tập 5 trang 33 Toán 10 Tập 2

Vận dụng trang 34 Toán 10 Tập 2
Việc quy đổi nhiệt độ giữa đơn vị độ C (Anders Celsius, 1701 – 1744) và đơn vị độ F (Daniel Fahrenheit, 1686 – 1736) được xác định bởi hai mốc sau. Vận dụng trang 34 Toán 10 Tập 2
Giải bài tập Bài 20: Vị trí tương đối giữa hai đường thẳng. Góc và khoảng cách

Bài 7.9 trang 41 Toán 10 Tập 2
Trong mặt phẳng tọa độ Oxy, cho điểm A(0; – 2) và đường thẳng ∆: x + y – 4 = 0. Bài 7.9 trang 41 Toán 10 Tập 2

Bài 7.10 trang 41 Toán 10 Tập 2
Trong mặt phẳng tọa độ, cho tam giác ABC có A(1; 0), B(3; 2) và C(– 2; – 1). Bài 7.10 trang 41 Toán 10 Tập 2
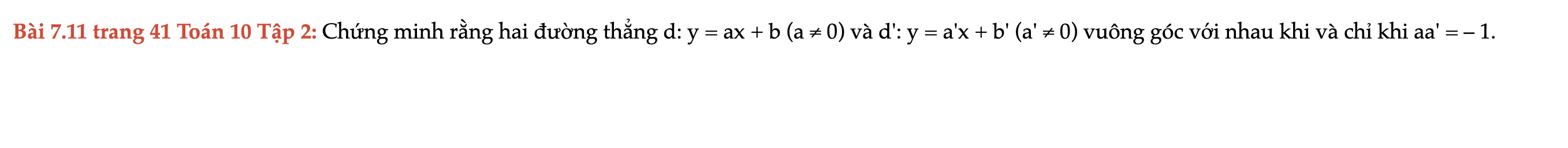
Bài 7.11 trang 41 Toán 10 Tập 2
Chứng minh rằng hai đường thẳng d: y = ax + b (a ≠ 0) và d': y = a'x + b' (a' ≠ 0) vuông góc với nhau khi và chỉ khi aa' = – 1. Bài 7.11 trang 41 Toán 10 Tập 2

Bài 7.12 trang 41 Toán 10 Tập 2
Trong mặt phẳng tọa độ, một tín hiệu âm thanh phát đi từ một vị trí và được ba thiết bị ghi tín hiệu đặt tại ba vị trí O(0; 0), A(1; 0), B(1; 3) nhận được cùng một thời điểm. Hãy xác định vị trí phát tín hiệu âm thanh. Bài 7.12 trang 41 Toán 10 Tập 2

Bài 7.7 trang 41 Toán 10 Tập 2
Xét vị trí tương đối giữa các cặp đường thẳng sau. Bài 7.7 trang 41 Toán 10 Tập 2

Bài 7.8 trang 41 Toán 10 Tập 2
Tính góc giữa các cặp đường thẳng sau. Bài 7.8 trang 41 Toán 10 Tập 2

Mở đầu trang 36 Toán 10 Tập 2
Trong mặt phẳng tọa độ, mỗi đường thẳng đều có đối tượng đại số tương ứng, gọi là phương trình của nó. Vậy các yếu tố liên quan tới đường thẳng được thể hiện như thế nào qua phương trình tương ứng? Mở đầu trang 36 Toán 10 Tập 2

HĐ1 trang 36 Toán 10 Tập 2
Trong mặt phẳng tọa độ, cho hai đường thẳng ∆1 và ∆2. Điểm M(1; 2) có thuộc cả hai đường thẳng nói trên hay không? HĐ1 trang 36 Toán 10 Tập 2

Luyện tập 1 trang 37 Toán 10 Tập 2
Xét vị trí tương đối giữa các cặp đường thẳng sau. Luyện tập 1 trang 37 Toán 10 Tập 2

HĐ2 trang 37 Toán 10 Tập 2
Hai đường thẳng ∆1 và ∆2 cắt nhau tạo thành bốn góc (H.7.6). Các số đo của bốn góc đó có mối quan hệ gì với nhau? HĐ2 trang 37 Toán 10 Tập 2
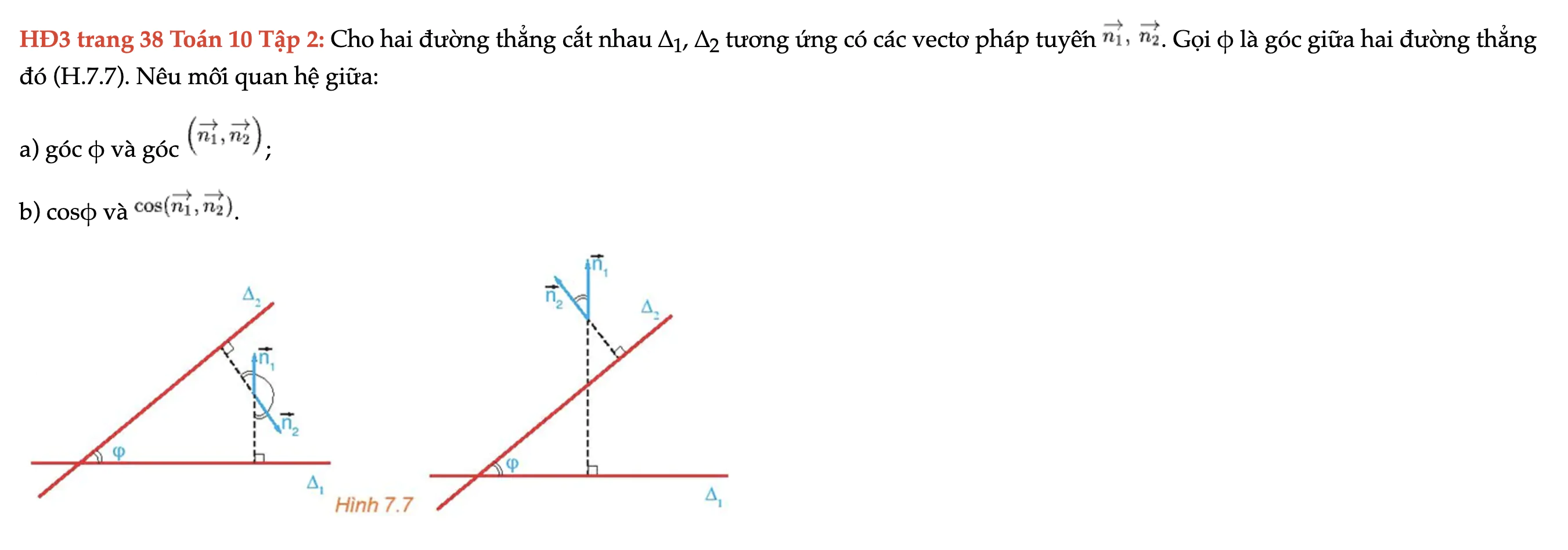
HĐ3 trang 38 Toán 10 Tập 2
Cho hai đường thẳng cắt nhau ∆1, ∆2 tương ứng có các vectơ pháp tuyến n1, n2. Gọi φ là góc giữa hai đường thẳng đó (H.7.7). HĐ3 trang 38 Toán 10 Tập 2

Luyện tập 2 trang 38 Toán 10 Tập 2
Tính góc giữa hai đường thẳng sau đây. Luyện tập 2 trang 38 Toán 10 Tập 2
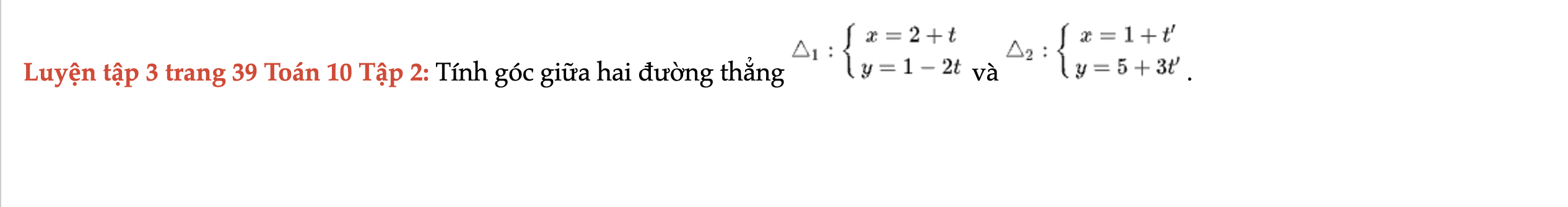
Luyện tập 3 trang 39 Toán 10 Tập 2
Tính góc giữa hai đường thẳng sau đây. Luyện tập 3 trang 39 Toán 10 Tập 2

Luyện tập 4 trang 39 Toán 10 Tập 2
Cho đường thẳng ∆: y = ax + b với a ≠ 0. Chứng minh rằng ∆ cắt trục hoành. Lập phương trình đường thẳng ∆0 đi qua O(0; 0) và song song (hoặc trùng) với ∆. Luyện tập 4 trang 39 Toán 10 Tập 2

HĐ4 trang 40 Toán 10 Tập 2
Cho điểm M(x0; y0) và đường thẳng ∆: ax + by + c = 0 có vectơ pháp tuyến n = (a;b). Gọi H là hình chiếu vuông góc của M trên ∆ (H.7.9). HĐ4 trang 40 Toán 10 Tập 2

Trải nghiệm trang 40 Toán 10 Tập 2
Đo trực tiếp khoảng cách từ điểm M đến đường thẳng ∆ (H.7.10) và giải thích vì sao kết quả đo đạc đó phù hợp với kết quả tính toán trong lời giải Ví dụ 4. Trải nghiệm trang 40 Toán 10 Tập 2

Luyện tập 5 trang 40 Toán 10 Tập 2
Tính khoảng cách từ điểm M(1; 2) đến đường thẳng Δ. Luyện tập 5 trang 40 Toán 10 Tập 2

Vận dụng trang 41 Toán 10 Tập 2
Nhân dịp nghỉ hè, Nam về quê ở với ông bà nội. Nhà ông bà nội có một ao cá có dạng hình chữ nhật ABCD với chiều dài AD = 15 m, chiều rộng AB = 12 m. Vận dụng trang 41 Toán 10 Tập 2
Giải bài tập Bài 21: Đường tròn trong mặt phẳng tọa độ
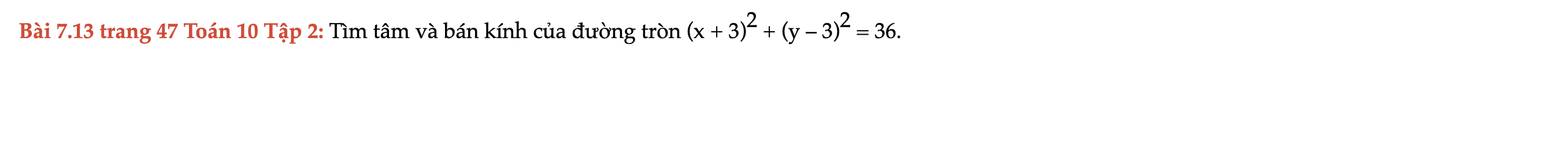
Bài 7.13 trang 47 Toán 10 Tập 2
Tìm tâm và bán kính của đường tròn. Bài 7.13 trang 47 Toán 10 Tập 2

Bài 7.14 trang 47 Toán 10 Tập 2
Hãy cho biết phương trình nào dưới đây là phương trình của một đường tròn và tìm tâm, bán kính của đường tròn tương ứng. Bài 7.14 trang 47 Toán 10 Tập 2

Bài 7.15 trang 47 Toán 10 Tập 2
Viết phương trình của đường tròn trong mỗi trường hợp sau. Bài 7.15 trang 47 Toán 10 Tập 2

Bài 7.16 trang 47 Toán 10 Tập 2
Trong mặt phẳng tọa độ, cho tam giác ABC, với A(6; – 2), B(4; 2), C(5; –5). Viết phương trình đường tròn ngoại tiếp tam giác đó. Bài 7.16 trang 47 Toán 10 Tập 2

Bài 7.17 trang 47 Toán 10 Tập 2
Cho đường tròn (C), viết phương trình tiếp tuyến d của (C) tại điểm M(0; 2). Bài 7.17 trang 47 Toán 10 Tập 2

Bài 7.18 trang 47 Toán 10 Tập 2
Chuyển động của một vật thể trong khoảng thời gian 180 phút được thể hiện trong mặt phẳng tọa độ. Theo đó, tại thời điểm t (0 ≤ t ≤ 180) vật thể ở vị trí có tọa độ (2 + sint°; 4 + cost°). Bài 7.18 trang 47 Toán 10 Tập 2

HĐ1 trang 43 Toán 10 Tập 2
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C), tâm I(a; b), bán kính R (H.7.13). Khi đó, một điểm M(x; y) thuộc đường tròn (C) khi và chỉ khi tọa độ của nó thỏa mãn điều kiện đại số nào? HĐ1 trang 43 Toán 10 Tập 2

Luyện tập 1 trang 44 Toán 10 Tập 2
Tìm tâm và bán kính của đường tròn (C). Luyện tập 1 trang 44 Toán 10 Tập 2

Luyện tập 2 trang 44 Toán 10 Tập 2
Hãy cho biết phương trình nào dưới đây là phương trình của một đường tròn. Tìm tâm và bán kính của đường tròn đó. Luyện tập 2 trang 44 Toán 10 Tập 2

Luyện tập 3 trang 45 Toán 10 Tập 2
Viết phương trình đường tròn (C) đi qua ba điểm M(4; – 5), N(2; – 1), P(3; – 8). Luyện tập 3 trang 45 Toán 10 Tập 2

Vận dụng 1 trang 45 Toán 10 Tập 2
Bên trong một hồ bơi, người ta dự định thiết kế hai bể sục nửa hình tròn bằng nhau và một bể sục hình tròn (H.7.15a) để người bơi có thể ngồi tựa lưng vào thành các bể sục thư giãn. Vận dụng 1 trang 45 Toán 10 Tập 2

HĐ2 trang 46 Toán 10 Tập 2
Cho đường tròn (C). Chứng minh điểm M(4; – 2) thuộc đường tròn (C). HĐ2 trang 46 Toán 10 Tập 2
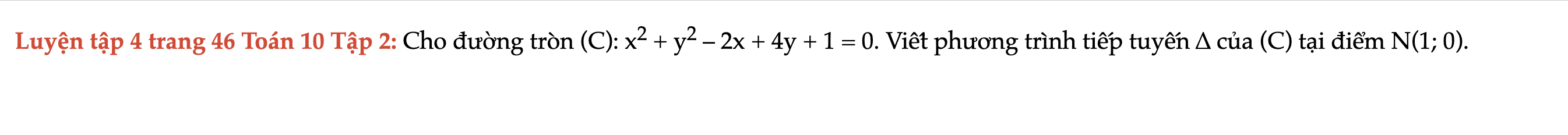
Luyện tập 4 trang 46 Toán 10 Tập 2
Cho đường tròn (C). Viết phương trình tiếp tuyến ∆ của (C) tại điểm N(1; 0). Luyện tập 4 trang 46 Toán 10 Tập 2

Vận dụng 2 trang 46 Toán 10 Tập 2
Trên mặt phẳng tọa độ Oxy, một vật chuyển động nhanh trên đường tròn có phương trình sau đây. Vận dụng 2 trang 46 Toán 10 Tập 2
Giải bài tập Bài 22: Ba đường conic

Bài 7.19 trang 56 Toán 10 Tập 2
Cho elip có phương trình sau, tìm tiêu điểm và tiêu cự của elip. Bài 7.19 trang 56 Toán 10 Tập 2

Bài 7.20 trang 56 Toán 10 Tập 2
Cho hypebol có phương trình sau, tìm tiêu điểm và tiêu cự của hypebol. Bài 7.20 trang 56 Toán 10 Tập 2

Bài 7.21 trang 56 Toán 10 Tập 2
Cho parabol có phương trình sau, tìm tiêu điểm và đường chuẩn của parabol. Bài 7.21 trang 56 Toán 10 Tập 2

Bài 7.22 trang 56 Toán 10 Tập 2
Lập phương trình chính tắc của elip đi qua điểm A(5; 0) và có một tiêu điểm là F2(3; 0). Bài 7.22 trang 56 Toán 10 Tập 2

Bài 7.23 trang 56 Toán 10 Tập 2
Lập phương trình chính tắc của parabol đi qua điểm M(2; 4). Bài 7.23 trang 56 Toán 10 Tập 2

Bài 7.24 trang 56 Toán 10 Tập 2
Có hai trạm phát tín hiệu vô tuyến đặt tại hai vị trí A, B cách nhau 300 km. Tại cùng một thời điểm, hai trạm cùng phát tín hiệu với vận tốc 292 000 km/s để một tàu thủy thu và đo độ lệch thời gian. Bài 7.24 trang 56 Toán 10 Tập 2

Bài 7.25 trang 56 Toán 10 Tập 2
Khúc cua của một con đường có dạng hình parabol, điểm đầu vào khúc cua là A, điểm cuối là B, khoảng cách AB = 400 m. Đỉnh parabol (P) của khúc của cách đường thẳng AB một khoảng 20 m và cách đều A, B. Bài 7.25 trang 56 Toán 10 Tập 2

HĐ1 trang 48 Toán 10 Tập 2
Đính hai đầu của một sợi dây không đàn hồi vào hai vị trí cố định F1, F2 trên một mặt bàn (độ dài sợi dây lớn hơn khoảng cách giữa hai điểm F1, F2 ). HĐ1 trang 48 Toán 10 Tập 2
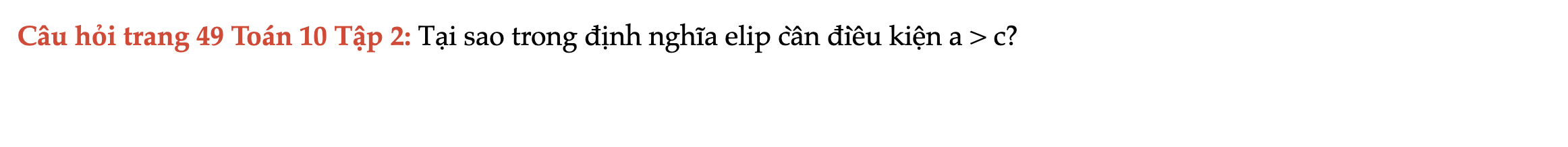
Câu hỏi trang 49 Toán 10 Tập 2
Tại sao trong định nghĩa elip cần điều kiện a > c? Câu hỏi trang 49 Toán 10 Tập 2

Luyện tập 1 trang 49 Toán 10 Tập 2
Trên bàn bida hình elip có một lỗ thu bi tại một tiêu điểm (H.7.20). Nếu gậy chơi tác động đủ mạnh vào một bi đặt tại tiêu điểm còn lại của bàn. Luyện tập 1 trang 49 Toán 10 Tập 2

HĐ2 trang 49 Toán 10 Tập 2
Xét một elip (E) với các kí hiệu như trong định nghĩa. Chọn hệ trục tọa độ Oxy có gốc O là trung điểm của F1F2, tia Ox trùng tia OF2 (H.7.21). Nêu tọa độ của các tiêu điểm F1, F2. HĐ2 trang 49 Toán 10 Tập 2
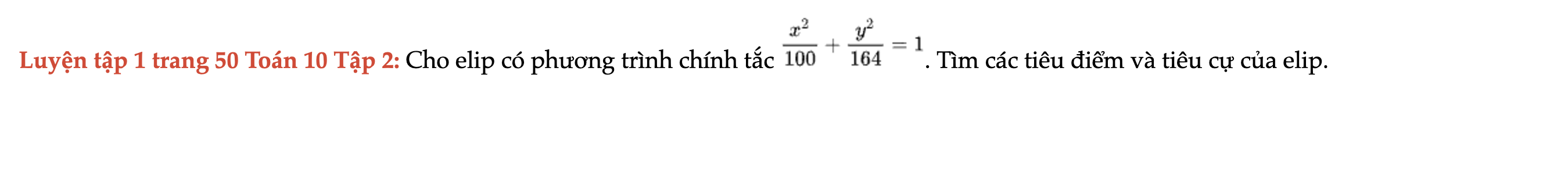
Luyện tập 1 trang 50 Toán 10 Tập 2
Cho elip có phương trình chính tắc sau đây. Tìm các tiêu điểm và tiêu cự của elip. Luyện tập 1 trang 50 Toán 10 Tập 2

Vận dụng 1 trang 50 Toán 10 Tập 2
Trong bản vẽ thiết kế, vòm của ô thoáng trong Hình 7.22 là nửa nằm phía trên trục hoành của elip có phương trình sau. Vận dụng 1 trang 50 Toán 10 Tập 2

HĐ3 trang 50 Toán 10 Tập 2
Giả sử thiết bị tại F2 nhận được tín hiệu âm thanh sớm hơn thiết bị tại F1 là 2 giây và vận tốc âm thanh là 343 m/s. HĐ3 trang 50 Toán 10 Tập 2

Câu hỏi trang 50 Toán 10 Tập 2
Tại sao trong định nghĩa hypebol cần điều kiện a < c? Câu hỏi trang 50 Toán 10 Tập 2

Luyện tập 3 trang 51 Toán 10 Tập 2
Cho hình chữ nhật ABCD và M, N tương ứng là trung điểm của các cạnh AB, CD (H.7.25). Chứng minh rằng bốn điểm A, B, C, D cùng thuộc một hypebol có hai tiêu điểm là M và N. Luyện tập 3 trang 51 Toán 10 Tập 2

HĐ4 trang 51 Toán 10 Tập 2
Xét một hypebol (H) với các kí hiệu như trong định nghĩa. Chọn hệ trục Oxy có gốc O là trung điểm của F1F2, tia Ox trùng tia OF2 (H.7.26). HĐ4 trang 51 Toán 10 Tập 2
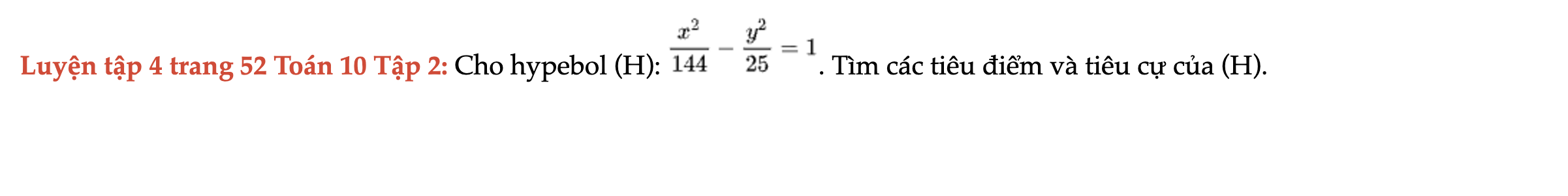
Luyện tập 4 trang 52 Toán 10 Tập 2
Cho hypebol (H). Tìm các tiêu điểm và tiêu cự của (H). Luyện tập 4 trang 52 Toán 10 Tập 2

HĐ5 trang 52 Toán 10 Tập 2
Cho parabol (P). Xét F(0; 1) và đường thẳng Δ: y + 1 = 0. Với điểm M(x; y) bất kì, chứng minh rằng MF = d(M, Δ) ⇔ M(x; y) thuộc (P). HĐ5 trang 52 Toán 10 Tập 2

HĐ6 trang 52 Toán 10 Tập 2
Hoạt động 6 trang 52 SGK Toán lớp 10 Tập 2: Xét (P) là một parabol với tiêu điểm F và đường chuẩn Δ. Gọi p là tham số tiêu của (P) và H là hình chiếu vuông góc của F trên Δ. HĐ6 trang 52 Toán 10 Tập 2

Vận dụng 2 trang 53 Toán 10 Tập 2
Tại một vùng biển giữa đất liền và một đảo, người ta phân định một đường ranh giới cách đều đất liền và đảo (H.7.28). Vận dụng 2 trang 53 Toán 10 Tập 2

Vận dụng 3 trang 56 Toán 10 Tập 2
Gương elip trong một máy tán sỏi thận (H.7.33) ứng với elip có phương trình chính tắc sau đây (theo đơn vị cm). Vận dụng 3 trang 56 Toán 10 Tập 2
Giải bài tập Bài tập cuối chương 7

Bài 7.26 trang 59 Toán 10 Tập 2
Phương trình nào sau đây là phương trình tham số của đường thẳng. Bài 7.26 trang 59 Toán 10 Tập 2

Bài 7.27 trang 59 Toán 10 Tập 2
Phương trình nào sau đây là phương trình tổng quát của đường thẳng. Bài 7.27 trang 59 Toán 10 Tập 2

Bài 7.28 trang 59 Toán 10 Tập 2
Phương trình nào sau đây là phương trình của đường tròn. Bài 7.28 trang 59 Toán 10 Tập 2

Bài 7.29 trang 59 Toán 10 Tập 2
Phương trình nào sau đây là phương trình chính tắc của đường elip. Bài 7.29 trang 59 Toán 10 Tập 2

Bài 7.30 trang 59 Toán 10 Tập 2
Phương trình nào sau đây là phương trình chính tắc của đường hypebol. Bài 7.30 trang 59 Toán 10 Tập 2

Bài 7.31 trang 59 Toán 10 Tập 2
Phương trình nào sau đây là phương trình chính tắc của đường parabol. Bài 7.31 trang 59 Toán 10 Tập 2
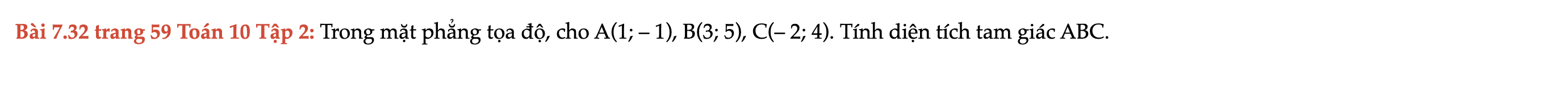
Bài 7.32 trang 59 Toán 10 Tập 2
Trong mặt phẳng tọa độ, cho A(1; – 1), B(3; 5), C(– 2; 4). Tính diện tích tam giác ABC. Bài 7.32 trang 59 Toán 10 Tập 2

Bài 7.33 trang 59 Toán 10 Tập 2
Trong mặt phẳng tọa độ, cho hai điểm A(– 1; 0) và B(3; 1); viết phương trình đường tròn tâm A và đi qua B. Bài 7.33 trang 59 Toán 10 Tập 2

Bài 7.34 trang 59 Toán 10 Tập 2
Cho đường tròn (C) có phương trình tìm tọa độ tâm I và bán kính R của (C). Bài 7.34 trang 59 Toán 10 Tập 2

Bài 7.35 trang 59 Toán 10 Tập 2
Cho elip (E) tìm các giao điểm A1, A2 của (E) với trục hoành và các giao điểm B1, B2 của (E) với trục tung. Tính A1A2, B1B2. Bài 7.35 trang 59 Toán 10 Tập 2

Bài 7.36 trang 59 Toán 10 Tập 2
Cho hypebol có phương trình tìm các giao điểm A1, A2 của hypebol với trục hoành (hoành độ của A1 nhỏ hơn của A2). Bài 7.36 trang 59 Toán 10 Tập 2

Bài 7.37 trang 59 Toán 10 Tập 2
Một cột trụ hình hypebol, có chiều cao 6 m, chỗ nhỏ nhất ở chính giữa và rộng 0,8 m, đỉnh cột và đáy cột đều rộng 1 m. Tính độ rộng của cột ở độ cao 5 m. Bài 7.37 trang 59 Toán 10 Tập 2