Giải bài tập Bài 7.17 trang 47 Toán 10 Tập 2 | Toán 10 - Kết nối tri thức
Hướng dẫn giải chi tiết từng bước bài tập Bài 7.17 trang 47 Toán 10 Tập 2. Bài 21: Đường tròn trong mặt phẳng tọa độ. Toán 10 - Kết nối tri thức
Đề bài:
Bài 7.17 trang 47 Toán 10 Tập 2: Cho đường tròn (C): x2 + y2+ 2x – 4y + 4 = 0. Viết phương trình tiếp tuyến d của (C) tại điểm M(0; 2).
Đáp án và cách giải chi tiết:
Ta có: x2 + y2 + 2x – 4y + 4 = 0 ⇔ x2 + y2 – 2 . (– 1) . x – 2 . 2 . y + 4 = 0.
Các hệ số: a = – 1, b = 2, c = 4.
Khi đó đường tròn (C) có tâm I(– 1; 2).
Do 02 + 22 + 2 . 0 – 4 . 2 + 4 = 0 nên điểm M(0; 2) thuộc (C).
Tiếp tuyến d của (C) tại điểm M(0; 2) có vectơ pháp tuyến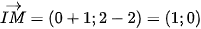
nên có phương trình d: 1(x – 0) + 0(y – 2) = 0 hay d: x = 0.
Nguồn: loigiaitoan.com
Tổng số đánh giá:
Xếp hạng: / 5 sao
Bài tập liên quan:
Bài 7.13 trang 47 Toán 10 Tập 2
Bài 7.13 trang 47 Toán 10 Tập 2: Tìm tâm và bán kính của đường tròn (x + 3)2 + (y – 3)2 = 36.
Bài 7.18 trang 47 Toán 10 Tập 2
Bài 7.18 trang 47 Toán 10 Tập 2: Chuyển động của một vật thể trong khoảng thời gian 180 phút được thể hiện trong mặt phẳng tọa độ. Theo đó, tại thời điểm t (0 ≤ t ≤ 180) vật thể ở vị trí có tọa độ (2 + sint°; 4 + cost°).
a) Tìm vị trí ban đầu và vị trí kết thúc của vật thể.
b) Tìm quỹ đạo chuyển động của vật thể.
HĐ1 trang 43 Toán 10 Tập 2
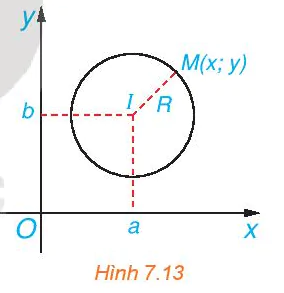
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C), tâm I(a; b), bán kính R (H.7.13). Khi đó, một điểm M(x; y) thuộc đường tròn (C) khi và chỉ khi tọa độ của nó thỏa mãn điều kiện đại số nào?
Luyện tập 1 trang 44 Toán 10 Tập 2
Tìm tâm và bán kính của đường tròn (C): (x + 2)2 + (y – 4)2 = 7.
Luyện tập 2 trang 44 Toán 10 Tập 2
Hãy cho biết phương trình nào dưới đây là phương trình của một đường tròn. Tìm tâm và bán kính của đường tròn đó.
a) x2 – y2 – 2x + 4y – 1 = 0;
b) x2 + y2 – 2x + 4y + 6 = 0;
c) x2 + y2 + 6x – 4y + 2 = 0.
Luyện tập 3 trang 45 Toán 10 Tập 2
Viết phương trình đường tròn (C) đi qua ba điểm M(4; – 5), N(2; – 1), P(3; – 8).
Vận dụng 1 trang 45 Toán 10 Tập 2
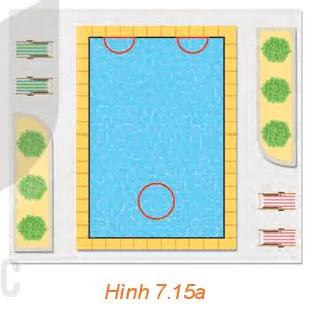
Bên trong một hồ bơi, người ta dự định thiết kế hai bể sục nửa hình tròn bằng nhau và một bể sục hình tròn (H.7.15a) để người bơi có thể ngồi tựa lưng vào thành các bể sục thư giãn. Hãy tìm bán kính của các bể sục để tổng chu vi của ba bể là 32 m mà tổng diện tích (chiếm hồ bơi) là nhỏ nhất. Trong tính toán, lấy π = 3,14, độ dài tính theo mét và làm tròn tới chữ số thập phân thứ hai.
HĐ2 trang 46 Toán 10 Tập 2
Cho đường tròn (C): (x – 1)2+ (y – 2)2 = 25 và điểm M(4; – 2).
a) Chứng minh điểm M(4; – 2) thuộc đường tròn (C).
b) Xác định tâm và bán kính của (C).
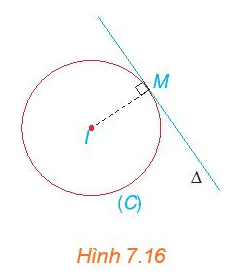
c) Gọi ∆ là tiếp tuyến của (C) tại M. Hãy chỉ ra một vectơ pháp tuyến của đường thẳng ∆ (H.7.16). Từ đó, viết phương trình đường thẳng ∆.
Luyện tập 4 trang 46 Toán 10 Tập 2
Cho đường tròn (C): x2 + y2 – 2x + 4y + 1 = 0. Viết phương trình tiếp tuyến ∆ của (C) tại điểm N(1; 0).
Vận dụng 2 trang 46 Toán 10 Tập 2
Trên mặt phẳng tọa độ Oxy, một vật chuyển động nhanh trên đường tròn có phương trình x2 + y2 = 25. Khi tới vị trí M(3; 4) thì vật bị văng khỏi quỹ đạo tròn và ngày sau đó, trong một khoảng thời gian ngắn bay theo hướng tiếp tuyến của đường tròn. Hỏi trong khoảng thời gian ngắn ngay sau khi văng, vật chuyển động trên đường thẳng nào?
Bài 7.14 trang 47 Toán 10 Tập 2
Bài 7.14 trang 47 Toán 10 Tập 2: Hãy cho biết phương trình nào dưới đây là phương trình của một đường tròn và tìm tâm, bán kính của đường tròn tương ứng.
a)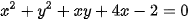 
;
b)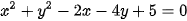 
;
c)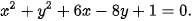 
Bài 7.15 trang 47 Toán 10 Tập 2
Bài 7.15 trang 47 Toán 10 Tập 2: Viết phương trình của đường tròn trong mỗi trường hợp sau:
a) Có tâm I(– 2; 5) và bán kính R = 7;
b) Có tâm I(1; – 2) và đi qua điểm A(– 2; 2);
c) Có đường kính AB, với A(– 1; – 3), B(– 3; 5);
d) Có tâm I(1; 3) và tiếp xúc với đường thẳng x + 2y + 3 = 0.
Bài 7.16 trang 47 Toán 10 Tập 2
Bài 7.16 trang 47 Toán 10 Tập 2: Trong mặt phẳng tọa độ, cho tam giác ABC, với A(6; – 2), B(4; 2), C(5; –5). Viết phương trình đường tròn ngoại tiếp tam giác đó.