Giải bài tập Toán 10 Chương 9: Phương pháp toạ độ trong mặt phẳng | Chân trời sáng tạo
Hướng dẫn giải Chương 9: Phương pháp toạ độ trong mặt phẳng
Giải bài tập Bài 1: Toạ độ của vectơ

Bài 1 trang 44 Toán lớp 10 Tập 2
Trên trục cho các điểm A, B, C, D có tọa độ lần lượt là 4; -1; -5; 0; vẽ trục và biểu diễn các điểm đã cho trên trục đó. Bài 1 trang 44 Toán lớp 10 Tập 2

Bài 2 trang 45 Toán lớp 10 Tập 2
Chứng minh hai vectơ ngược hướng, hai vectơ cùng hướng, hai vectơ đối nhau. Bài 2 trang 45 Toán lớp 10 Tập 2

Bài 3 trang 45 Toán lớp 10 Tập 2
Tìm tọa độ của các vectơ. Bài 3 trang 45 Toán lớp 10 Tập 2

Bài 4 trang 45 Toán lớp 10 Tập 2
Cho bốn điểm A(3; 5), B(4;0), C(0; -3), D(2; 2); trong các điểm đã cho, hãy tìm điểm thuộc trục hoành. Bài 4 trang 45 Toán lớp 10 Tập 2

Bài 5 trang 45 Toán lớp 10 Tập 2
Cho điểm M, tìm tọa độ điểm H là hình chiếu vuông góc của điểm M trên trục Ox. Bài 5 trang 45 Toán lớp 10 Tập 2

Bài 6 trang 45 Toán lớp 10 Tập 2
Cho ba điểm A(2; 2), B(3; 5), C(5; 5); tìm tọa độ điểm D sao cho ABCD là một hình bình hành. Bài 6 trang 45 Toán lớp 10 Tập 2

Bài 7 trang 45 Toán lớp 10 Tập 2
Cho tam giác ABC có các điểm M(2; 2), N(3; 4), P(5; 3) lần lượt là trung điểm của các cạnh AB, BC và CA; tìm tọa độ các đỉnh của tam giác ABC. Bài 7 trang 45 Toán lớp 10 Tập 2

Bài 8 trang 45 Toán lớp 10 Tập 2
Cho hai điểm A(1; 3), B(4; 2); tìm tọa độ điểm D nằm trên trục Ox sao cho DA = DB. Bài 8 trang 45 Toán lớp 10 Tập 2

Bài 9 trang 45 Toán lớp 10 Tập 2
Tính góc giữa hai vectơ a và b trong các trường hợp sau. Bài 9 trang 45 Toán lớp 10 Tập 2

Bài 10 trang 45 Toán lớp 10 Tập 2
Cho bốn điểm A(7; -3), B(8; 4), C(1; 5), D(0; -2); chứng minh rằng tứ giác ABCD là hình vuông. Bài 10 trang 45 Toán lớp 10 Tập 2
Bài 11 trang 45 Toán lớp 10 Tập 2
Một máy bay đang hạ cánh với vận tốc v, cho biết vận tốc của gió là w và một đơn vị trên hệ trục tọa độ tương ứng với 1km; tìm độ dài vectơ tổng hai vận tốc v và w. Bài 11 trang 45 Toán lớp 10 Tập 2

Hoạt động khởi động trang 38 Toán lớp 10 Tập 2
Hoạt động khởi động trang 38 Toán lớp 10 Tập 2: Tìm cách xác định vị trí các quân mã trên bàn cờ vua.
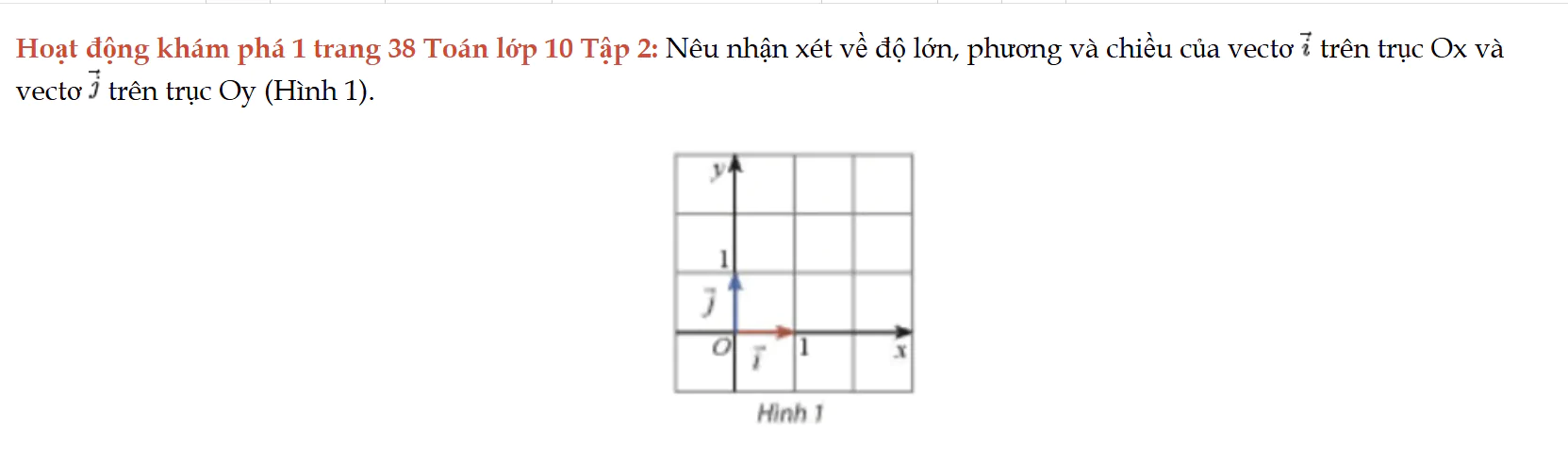
Hoạt động khám phá 1 trang 38 Toán lớp 10 Tập 2
Hoạt động khám phá 1 trang 38 Toán lớp 10 Tập 2: Nêu nhận xét về độ lớn, phương và chiều của vectơ
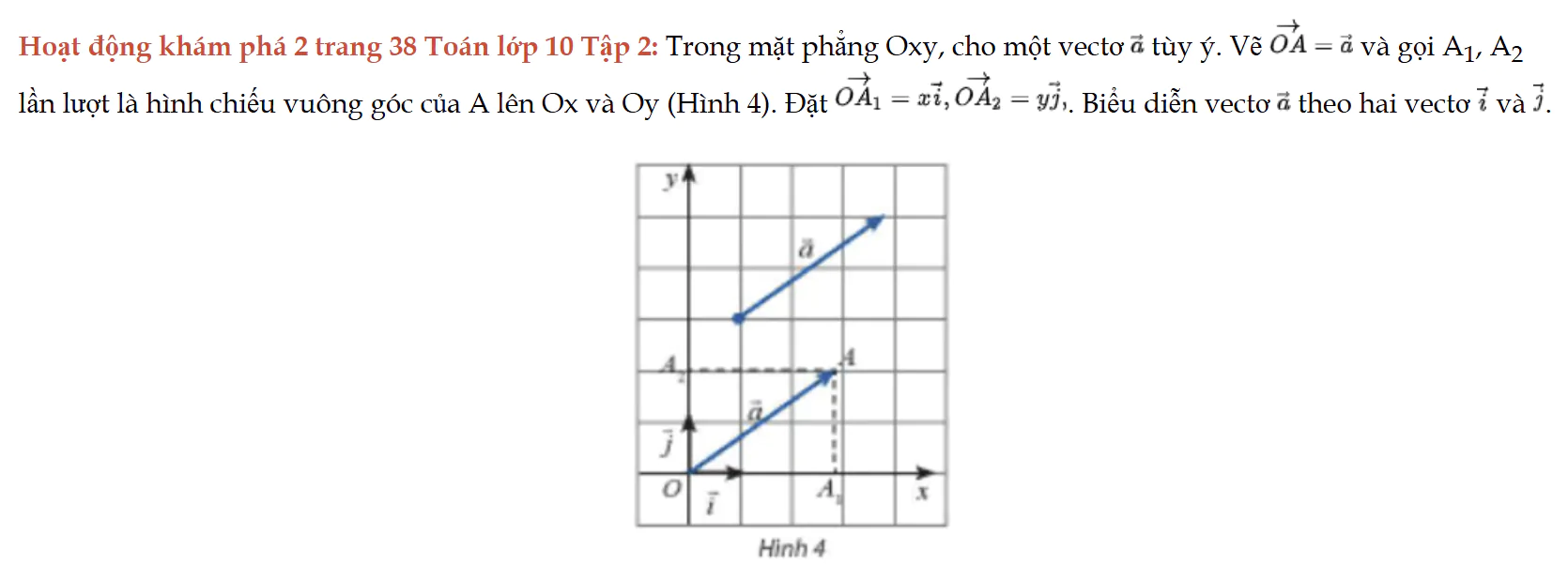
Hoạt động khám phá 2 trang 38 Toán lớp 10 Tập 2
Hoạt động khám phá 2 trang 38 Toán lớp 10 Tập 2

Hoạt động khám phá 3 trang 39 Toán lớp 10 Tập 2
Hoạt động khám phá 3 trang 39 Toán lớp 10 Tập 2: Trong mặt phẳng tọa độ, cho điểm M. Xác định tọa độ của vectơ

Hoạt động khám phá 4 trang 40 Toán lớp 10 Tập 2
Hoạt động khám phá 4 trang 40 Toán lớp 10 Tập 2

Hoạt động khám phá 5 trang 41 Toán lớp 10 Tập 2
Hoạt động khám phá 5 trang 41 Toán lớp 10 Tập 2: tìm tọa độ vecto

Hoạt động khám phá 6 trang 42 Toán lớp 10 Tập 2
Hoạt động khám phá 6 trang 42 Toán lớp 10 Tập 2

Thực hành 1 trang 40 Toán lớp 10 Tập 2
Thực hành 1 trang 40 Toán lớp 10 Tập 2

Vận dụng 1 trang 40 Toán lớp 10 Tập 2
Một máy bay đang cất cánh với vận tốc 240km/h theo phương hợp với phương nằm ngang một góc 30° (Hình 7).Vận dụng 1 trang 40 Toán lớp 10 Tập 2
Thực hành 2 trang 41 Toán lớp 10 Tập 2
Cho hai vectơ m = (-6; 1) và n = (0; 2). Tìm tọa độ của các vectơ sau. Tính các tích vô hướng sau. Thực hành 2 trang 41 Toán lớp 10 Tập 2

Vận dụng 2 trang 41 Toán lớp 10 Tập 2
Một thiết bị thăm dò đáy biển đang lặn với vận tốc vectơ v = (10; -8) (Hình 8). Cho viết vận tốc của dòng hải lưu vùng biển là vectơ w = (3,5; 0). Vận dụng 2 trang 41 Toán lớp 10 Tập 2

Thực hành 3 trang 42 Toán lớp 10 Tập 2
Cho E((9; 9), F(8; -7), G(0; -6). Tìm tọa độ của các vectơ FE, FG, EG. Thực hành 3 trang 42 Toán lớp 10 Tập 2

Thực hành 4 trang 43 Toán lớp 10 Tập 2
Cho tam giác QRS có tọa độ các đỉnh là Q(7; -2), R(-4; 9) và S(5; 8). Tìm tọa độ trung điểm M của cạnh QS. Tìm tọa độ trọng tâm G của tam giác QRS. Thực hành 4 trang 43 Toán lớp 10 Tập 2

Hoạt động khám phá 7 trang 43 Toán lớp 10 Tập 2
Cho hai vectơ a = (a1; a2), b = (b1; b2) và hai điểm A(xA; yA), B(xB; yB). Hoàn thành các phép biến đổi sau. Hoạt động khám phá 7 trang 43 Toán lớp 10 Tập 2

Thực hành 5 trang 44 Toán lớp 10 Tập 2
Trong mặt phẳng Oxy, cho tam giác DEF có tọa độ đỉnh là D(2; 2), E(6; 2) và F(2; 6). Tìm tọa độ điểm H là chân đường cao của tam giác DEF kẻ từ D. Giải tam giác DEF. Thực hành 5 trang 44 Toán lớp 10 Tập 2

Vận dụng 3 trang 44 Toán lớp 10 Tập 2
Một trò chơi trên máy tính đang mô phỏng một vùng biển có hai hòn đảo nhỏ có tọa độ B(50; 30) và C(32; -23). Một con tàu đang neo đậu tại điểm A(-10; 20). Vận dụng 3 trang 44 Toán lớp 10 Tập 2
Giải bài tập Bài 2: Đường thẳng trong mặt phẳng toạ độ

Bài 1 trang 57 Toán lớp 10 Tập 2
Lập phương trình tham số và phương trình tổng quát của đường thẳng d trong mỗi trường hợp sau. Bài 1 trang 57 Toán lớp 10 Tập 2

Bài 2 trang 57 Toán lớp 10 Tập 2
Cho tam giác ABC, biết A(2; 5), B(1; 2) và C(5; 4); lập phương trình tổng quát của đường thẳng BC. Bài 2 trang 57 Toán lớp 10 Tập 2

Bài 3 trang 57 Toán lớp 10 Tập 2
Lập phương trình tham số và phương trình tổng quát của đường thẳng ∆ trong các trường hợp; ∆ đi qua A(2; 1) và song song với đường thẳng 3x + y + 9 = 0. Bài 3 trang 57 Toán lớp 10 Tập 2
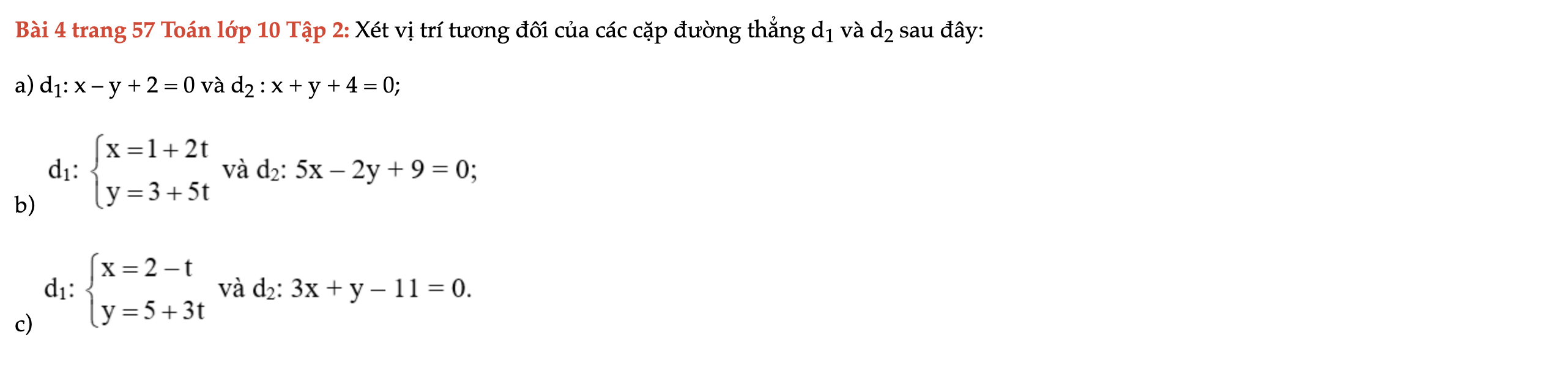
Bài 4 trang 57 Toán lớp 10 Tập 2
Xét vị trí tương đối của các cặp đường thẳng d1 và d2; d1: x – y + 2 = 0 và d2 : x + y + 4 = 0. Bài 4 trang 57 Toán lớp 10 Tập 2
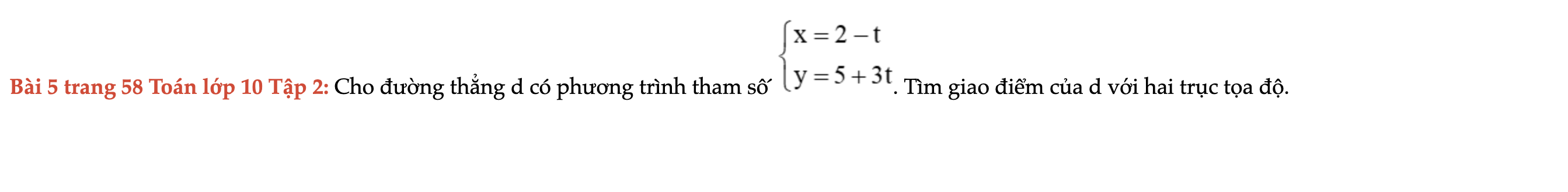
Bài 5 trang 58 Toán lớp 10 Tập 2
Cho đường thẳng d; tìm giao điểm của d với hai trục tọa độ. Bài 5 trang 58 Toán lớp 10 Tập 2

Bài 6 trang 58 Toán lớp 10 Tập 2
Tìm số đo của góc giữa hai đường thẳng d1 và d2 trong các trường hợp; d1: x – 2y + 3 = 0 và d2: 3x – y – 11 = 0. Bài 6 trang 58 Toán lớp 10 Tập 2

Bài 7 trang 58 Toán lớp 10 Tập 2
Tính khoảng cách từ điểm M đến đường thẳng ∆ trong các trường hợp; M(1; 2) và ∆: 3x – 4y + 12 = 0. Bài 7 trang 58 Toán lớp 10 Tập 2
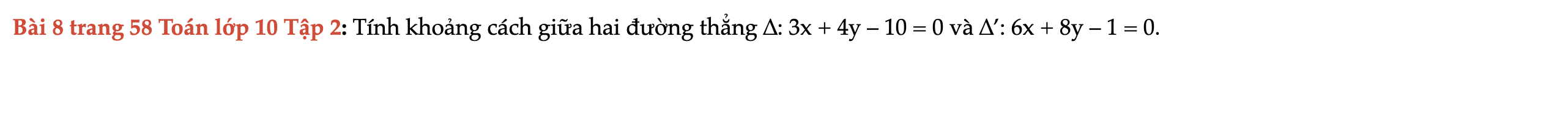
Bài 8 trang 58 Toán lớp 10 Tập 2
Tính khoảng cách giữa hai đường thẳng ∆: 3x + 4y – 10 = 0 và ∆’: 6x + 8y – 1 = 0. Bài 8 trang 58 Toán lớp 10 Tập 2

Bài 9 trang 58 Toán lớp 10 Tập 2
Trong mặt phẳng Oxy, cho điểm S(x; y) di động trên đường thẳng d: 12x – 5y + 16 = 0; tính khoảng cách ngắn nhất từ điểm M(5;10) đến điểm S. Bài 9 trang 58 Toán lớp 10 Tập 2
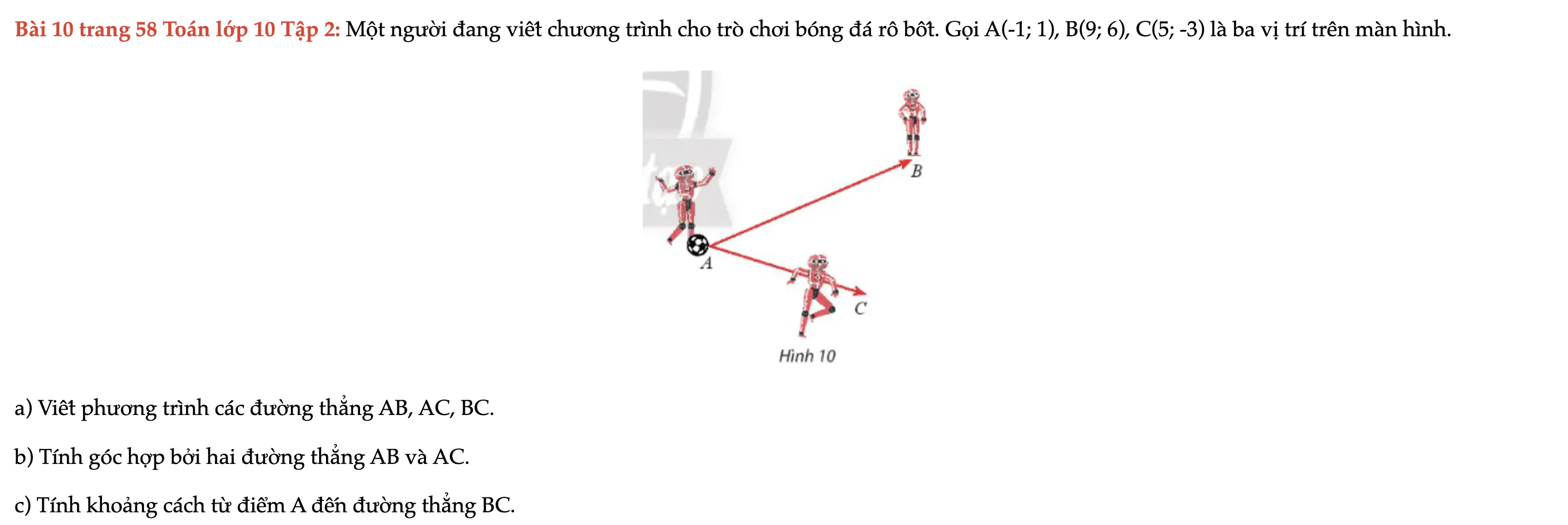
Bài 10 trang 58 Toán lớp 10 Tập 2
Một người đang viết chương trình cho trò chơi bóng đá rô bốt, gọi A(-1; 1), B(9; 6), C(5; -3) là ba vị trí trên màn hình; viết phương trình các đường thẳng AB, AC, BC. Bài 10 trang 58 Toán lớp 10 Tập 2
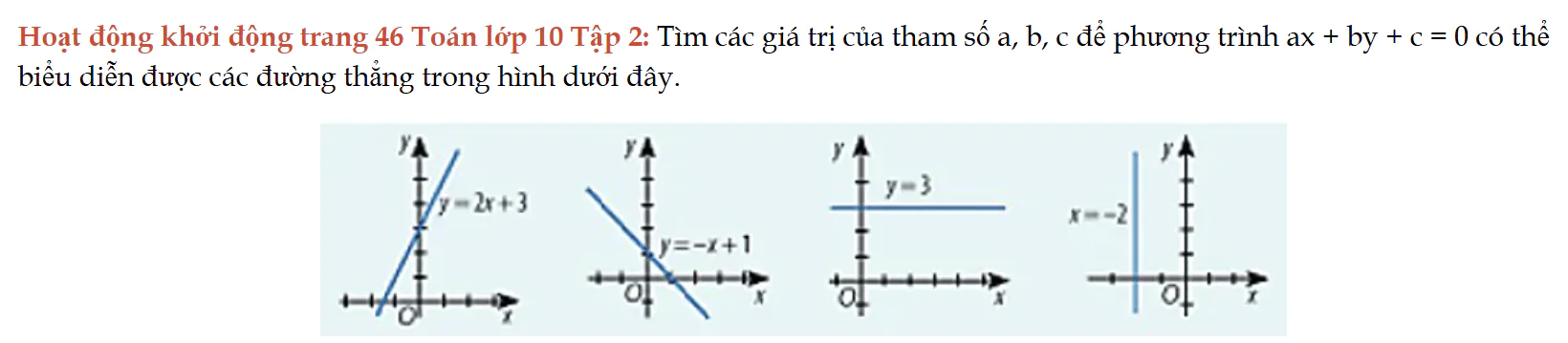
Hoạt động khởi động trang 46 Toán lớp 10 Tập 2
Hoạt động khởi động trang 46 Toán lớp 10 Tập 2: Tìm các giá trị của tham số a, b, c để phương trình ax + by + c = 0 có thể biểu diễn được các đường thẳng trong hình dưới đây.

Hoạt động khám phá 1 trang 46 Toán lớp 10 Tập 2
Trong mặt phẳng Oxy, cho đường thẳng ∆ đi qua điểm M0(x0; y0) và cho hai vectơ n = (a; b) và u = (-b; a) khác vectơ – không. Cho biết vectơ u có giá song song hoặc trùng với ∆. Hoạt động khám phá 1 trang 46 Toán lớp 10 Tập 2

Hoạt động khám phá 2 trang 47 Toán lớp 10 Tập 2
Trong mặt phẳng Oxy, cho đường thẳng ∆ đi qua điểm M0(x0; y0) và nhận vectơ u = (u1; u2) làm VTCP. Với mỗi điểm M(x; y) thuộc ∆, tìm tọa độ điểm M theo tọa độ M0 và vectơ u. Hoạt động khám phá 2 trang 47 Toán lớp 10 Tập 2

Thực hành 1 trang 47 Toán lớp 10 Tập 2
Viết phương trình tham số của đường thẳng d đi qua điểm B(-9; 5) và nhận vectơ v = (8; -4) làm vectơ chỉ phương. Thực hành 1 trang 47 Toán lớp 10 Tập 2

Vận dụng 1 trang 48 Toán lớp 10 Tập 2
Một trò chơi đua xe ô tô vượt xa mạc trên máy tính đã xác định trước một hệ trục tọa độ Oxy. Cho biết một ô tô chuyển động thẳng đều từ điểm M(1; 1) với vectơ vận tốc v = (40; 30). Vận dụng 1 trang 48 Toán lớp 10 Tập 2

Hoạt động khám phá 3 trang 48 Toán lớp 10 Tập 2
Trong mặt phẳng Oxy, cho đường thẳng ∆ đi qua điểm M0(x0; y0) và nhận vectơ n = (a; b) làm vectơ pháp tuyến. Với mỗi điểm M(x; y) thuộc ∆, chứng tỏ rằng điểm M(x; y) có tọa độ thỏa mãn phương trình. Hoạt động khám phá 3 trang 48 Toán lớp 10 Tập 2

Thực hành 2 trang 49 Toán lớp 10 Tập 2
Viết phương trình tham số và phương trình tổng quát của đường thẳng trong các trường hợp sau. Thực hành 2 trang 49 Toán lớp 10 Tập 2

Vận dụng 2 trang 49 Toán lớp 10 Tập 2
Một người đang lập trình một trò chơi trên máy tính. Trên màn hình máy tính đã xác định được một hệ trục tọa độ Oxy. Vận dụng 2 trang 49 Toán lớp 10 Tập 2

Thực hành 3 trang 51 Toán lớp 10 Tập 2
Tìm các hàm số bậc nhất có đồ thị là các đường thẳng trong thực hành 2. Thực hành 3 trang 51 Toán lớp 10 Tập 2

Vận dụng 3 trang 51 Toán lớp 10 Tập 2
Một người bắt đầu mở một vòi nước. Nước từ vòi chảy với tốc độ là 2m3/h vào một cái bể đã chứa sẵn 5m3 nước. Vận dụng 3 trang 51 Toán lớp 10 Tập 2
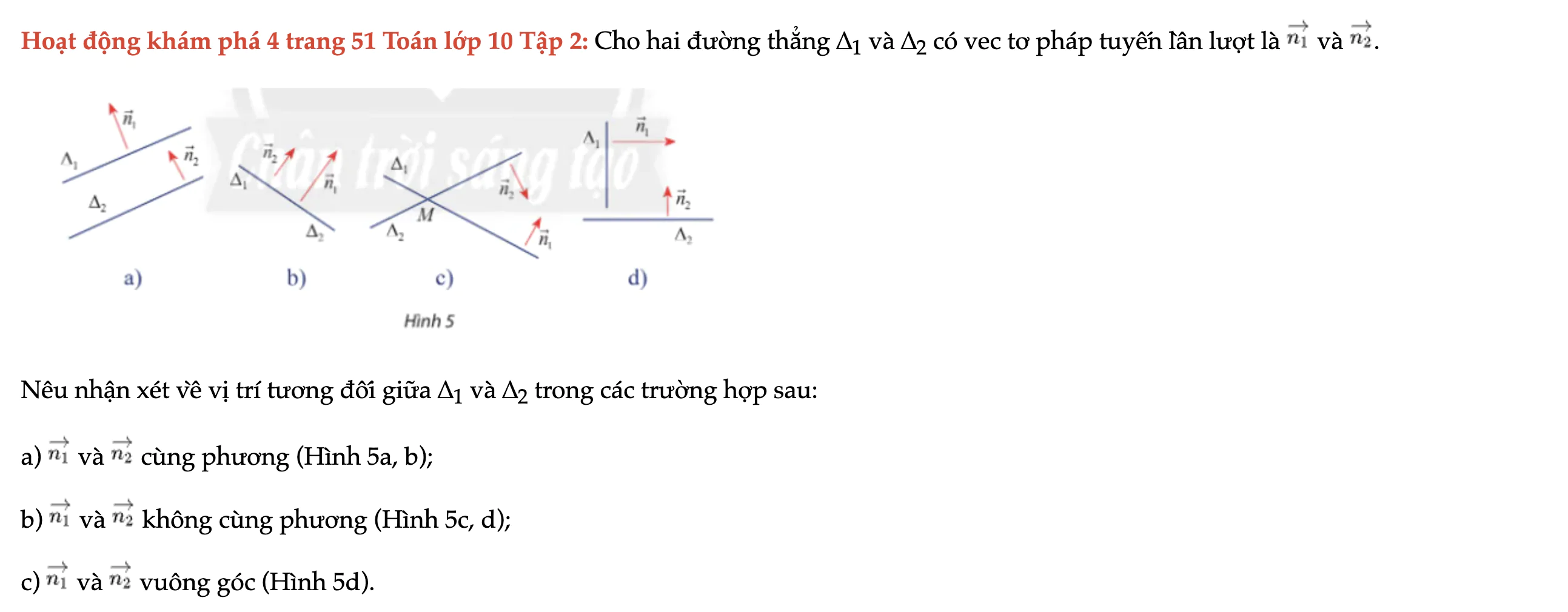
Hoạt động khám phá 4 trang 51 Toán lớp 10 Tập 2
Cho hai đường thẳng ∆1 và ∆2 có vec tơ pháp tuyến lần lượt là n1 và n2. Nêu nhận xét về vị trí tương đối giữa ∆1 và ∆2 trong các trường hợp sau. Hoạt động khám phá 4 trang 51 Toán lớp 10 Tập 2

Thực hành 4 trang 53 Toán lớp 10 Tập 2
Xét vị trí tương đối của các cặp đường thẳng d1 và d2 trong các trường hợp sau. Thực hành 4 trang 53 Toán lớp 10 Tập 2

Vận dụng 4 trang 53 Toán lớp 10 Tập 2
Viết phương trình đường thẳng d1 đi qua điểm A(2; 3) và song song với đường thẳng d2: x + 3y + 2 = 0. Vận dụng 4 trang 53 Toán lớp 10 Tập 2

Hoạt động khám phá 5 trang 54 Toán lớp 10 Tập 2
Cho hai đường thẳng xy và zt cắt nhau tại O và cho biết góc xOz = 38 độ (Hình 6). Tính số đo các góc xOt, tOy và yOz. Hoạt động khám phá 5 trang 54 Toán lớp 10 Tập 2

Hoạt động khám phá 6 trang 54 Toán lớp 10 Tập 2
Cho hai đường thẳng: ∆1: a1x + b1y + c1 = 0 và ∆2: a2x + b2y + c2 = 0 có vectơ pháp tuyến lần lượt là n1 và n2. Hoạt động khám phá 6 trang 54 Toán lớp 10 Tập 2

Thực hành 5 trang 56 Toán lớp 10 Tập 2
Tìm số đo của góc giữa hai đường thẳng ∆1 và ∆2 trong các trường hợp sau. Thực hành 5 trang 56 Toán lớp 10 Tập 2

Vận dụng 5 trang 56 Toán lớp 10 Tập 2
Tìm số đo của góc giữa hai đường thẳng là đồ thị của hai hàm số y = x và y = 2x + 1. Vận dụng 5 trang 56 Toán lớp 10 Tập 2

Hoạt động khám phá 7 trang 56 Toán lớp 10 Tập 2
Trong mặt phẳng Oxy, cho đường thẳng ∆: ax + by + c = 0 (a2 + b2 > 0) có vectơ pháp tuyến và cho điểm M0(x0; y0) có hình chiếu vuông góc H(xH; yH) trên ∆ (Hình 9). Hoạt động khám phá 7 trang 56 Toán lớp 10 Tập 2
Thực hành 6 trang 57 Toán lớp 10 Tập 2
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có tọa độ các đỉnh A(1; 1), B(5; 2), C(4; 4). Tính độ dài các đường cao của tam giác ABC. Thực hành 6 trang 57 Toán lớp 10 Tập 2
Vận dụng 6 trang 57 Toán lớp 10 Tập 2
Tính khoảng cách giữa hai đường thẳng d1: 4x – 3y + 2 = 0 và d2: 4x – 3y + 12 = 0. Vận dụng 6 trang 57 Toán lớp 10 Tập 2
Giải bài tập Bài 3: Đường tròn trong mặt phẳng toạ độ

Bài 1 trang 62 Toán lớp 10 Tập 2
Phương trình nào trong các phương trình sau đây là phương trình đường tròn, tìm tọa độ tâm và bán kính của đường tròn đó. Bài 1 trang 62 Toán lớp 10 Tập 2

Bài 2 trang 62 Toán lớp 10 Tập 2
Lập phương trình đường tròn (C) trong các trường hợp sau; (C) có tâm I(1; 5) có bán kính r = 4. Bài 2 trang 62 Toán lớp 10 Tập 2

Bài 3 trang 62 Toán lớp 10 Tập 2
Lập phương trình đường tròn ngoại tiếp tam giác có tọa độ các đỉnh là M(2; 5), N(1; 2), P(5; 4). Bài 3 trang 62 Toán lớp 10 Tập 2

Bài 4 trang 62 Toán lớp 10 Tập 2
Lập phương trình đường tròn tiếp xúc với hai trục tọa độ Ox, Oy và đi qua điểm A(4; 2). Bài 4 trang 62 Toán lớp 10 Tập 2
Bài 5 trang 63 Toán lớp 10 Tập 2
Cho đường tròn (C), chứng tỏ rằng điểm M(4; 6) thuộc đường tròn (C). Bài 5 trang 63 Toán lớp 10 Tập 2
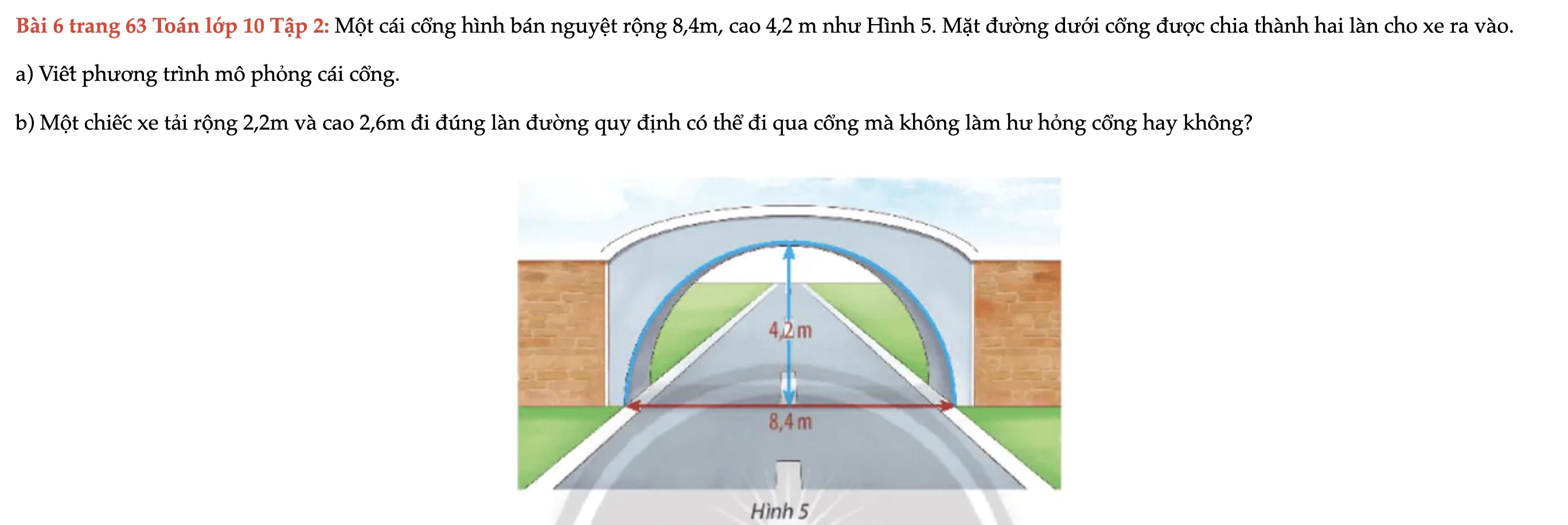
Bài 6 trang 63 Toán lớp 10 Tập 2
Một cái cổng hình bán nguyệt rộng 8,4m, cao 4,2 m như Hình 5. Mặt đường dưới cổng được chia thành hai làn cho xe ra vào; viết phương trình mô phỏng cái cổng. Bài 6 trang 63 Toán lớp 10 Tập 2

Hoạt động khởi động trang 59 Toán lớp 10 Tập 2
Hoạt động khởi động trang 59 Toán lớp 10 Tập 2: Làm thế nào để viết phương trình biểu diến tập hợp các điểm

Hoạt động khám phá 1 trang 59 Toán lớp 10 Tập 2
Hoạt động khám phá 1 trang 59 Toán lớp 10 Tập 2: Hãy nhắc lại công thức tính khoảng cách giữa hai điểm I(a; b) và M(x; y) nằm trong mặt phẳng Oxy.

Thực hành 2 trang 61 Toán lớp 10 Tập 2
Thực hành 2 trang 61 Toán lớp 10 Tập 2: Phương trình nào trong các phương trình sau đây là phương trình đường tròn? Tìm tọa độ tâm và bán kính của đường tròn đó.

Thực hành 3 trang 62 Toán lớp 10 Tập 2
Thực hành 3 trang 62 Toán lớp 10 Tập 2: Viết phương trình tiếp tuyến của đường tròn

Vận dụng 1 trang 61 Toán lớp 10 Tập 2
Vận dụng 1 trang 61 Toán lớp 10 Tập 2: Theo dữ kiện đã cho trong hoạt động của bài học, viết phương trình đường tròn biểu diễn tập hợp các điểm xa nhất mà vòi nước có thể phun tới.

Vận dụng 2 trang 61 Toán lớp 10 Tập 2
Vận dụng 2 trang 61 Toán lớp 10 Tập 2: Tìm tọa độ tâm và bán kính của đường tròn
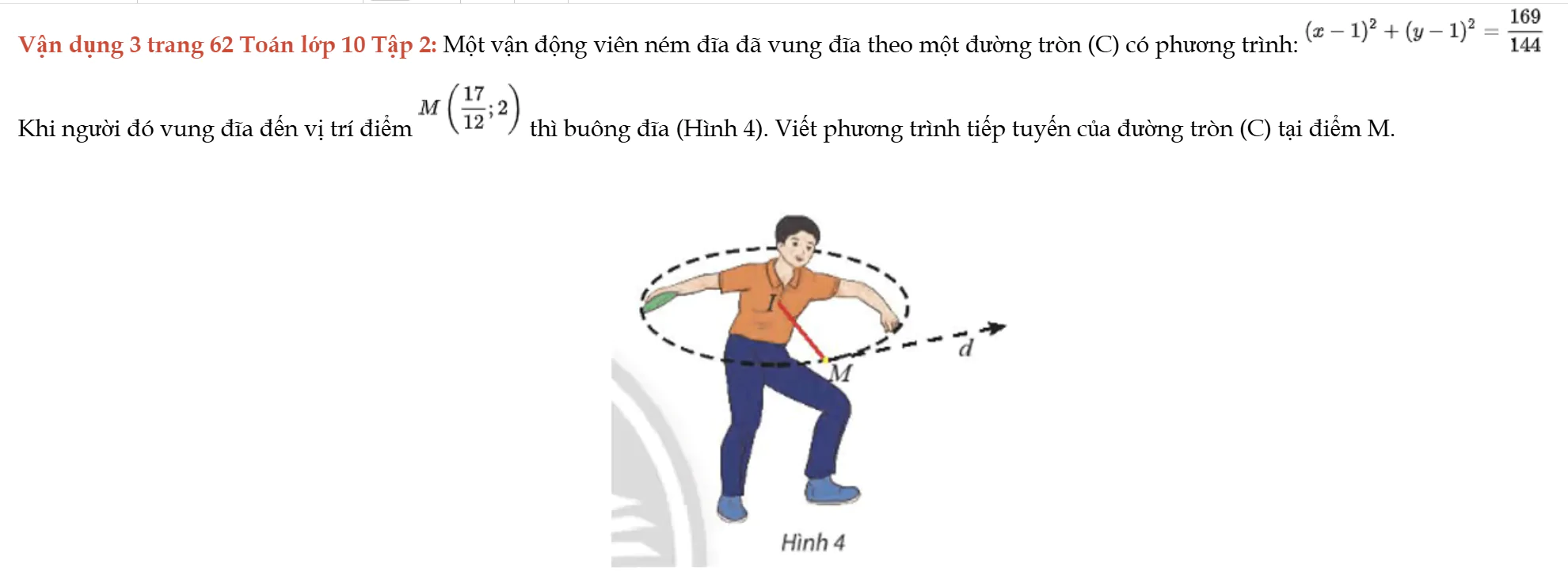
Vận dụng 3 trang 62 Toán lớp 10 Tập 2
Vận dụng 3 trang 62 Toán lớp 10 Tập 2

Thực hành 1 trang 60 Toán lớp 10 Tập 2
Viết phương trình đường tròn (C) trong các trường hợp sau. (C) có tâm O(0; 0), bán kính R = 4. Thực hành 1 trang 60 Toán lớp 10 Tập 2

Hoạt động khám phá 2 trang 61 Toán lớp 10 Tập 2
Cho điểm M(x0; y0) nằm trên đường tròn (C) tâm I(a; b) và cho điểm M(x; y) tùy ý trong mặt phẳng Oxy. Gọi ∆ là tiếp tuyến của (C) tại M0. Hoạt động khám phá 2 trang 61 Toán lớp 10 Tập 2
Giải bài tập Bài 4: Ba đường conic trong mặt phẳng toạ độ

Bài 1 trang 70 Toán lớp 10 Tập 2
Viết phương trình chính tắc của elip có trục lớn bằng 20 và trục nhỏ bằng 16. Bài 1 trang 70 Toán lớp 10 Tập 2

Bài 2 trang 70 Toán lớp 10 Tập 2
Viết phương trình chính tắc của các đường conic dưới đây; gọi tên và tìm tọa độ các tiêu điểm của chúng. Bài 2 trang 70 Toán lớp 10 Tập 2

Bài 3 trang 70 Toán lớp 10 Tập 2
Để cắt một bảng hiệu quảng cáo hình elip có trục lớn là 80 cm và trục nhỏ là 40 cm từ một tấm ván ép hình chữ nhật có kích thước 80 cm × 40 cm, người ta vẽ hình elip đó lên ván ép như hướng dẫn sau. Bài 3 trang 70 Toán lớp 10 Tập 2
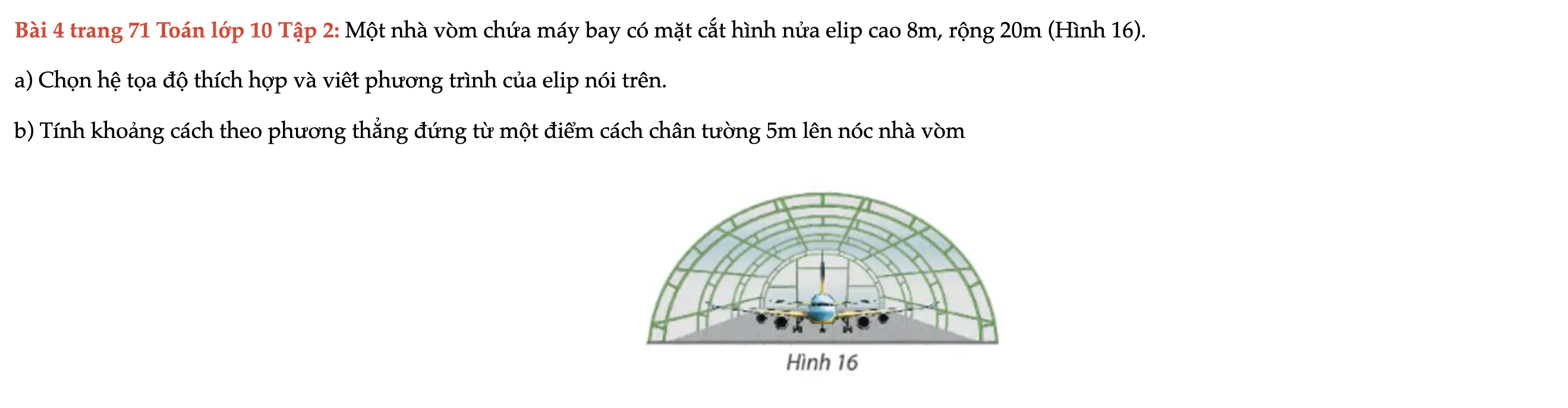
Bài 4 trang 71 Toán lớp 10 Tập 2
Một nhà vòm chứa máy bay có mặt cắt hình nửa elip cao 8m, rộng 20m, chọn hệ tọa độ thích hợp và viết phương trình của elip nói trên. Bài 4 trang 71 Toán lớp 10 Tập 2

Bài 5 trang 71 Toán lớp 10 Tập 2
Một tháp làm nguội của một nhà máy có mặt cắt là hình hypebol, biết chiều cao của tháp là 150m và khoảng cách từ nóc tháp đến tâm đối xứng của hypebol bằng 2/3 khoảng cách từ tâm đối xứng đến đáy. Bài 5 trang 71 Toán lớp 10 Tập 2
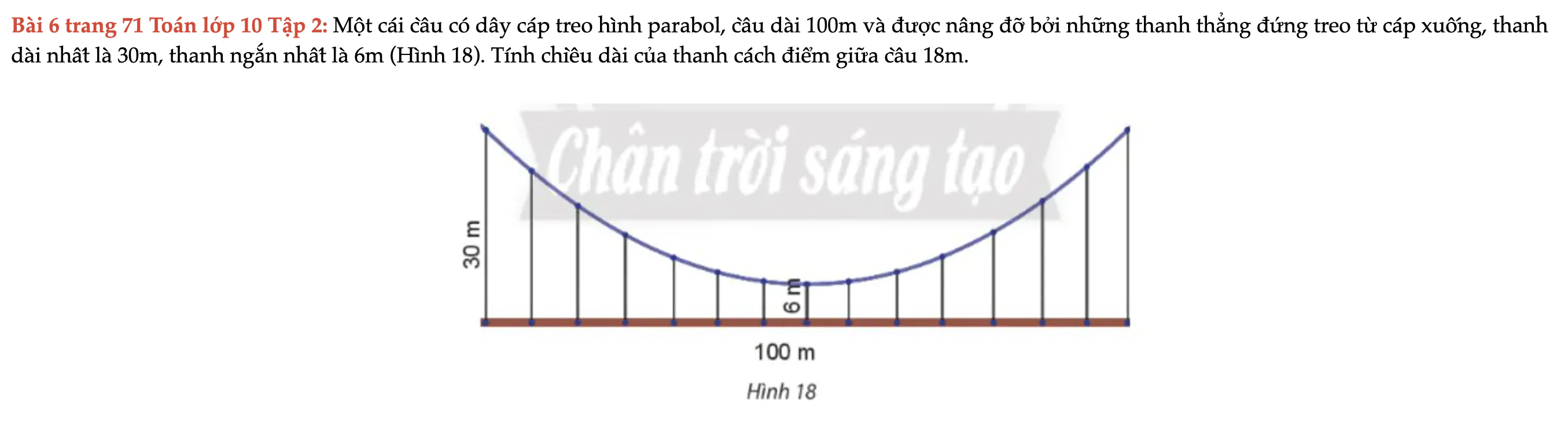
Bài 6 trang 71 Toán lớp 10 Tập 2
Một cái cầu có dây cáp treo hình parabol, cầu dài 100m và được nâng đỡ bởi những thanh thẳng đứng treo từ cáp xuống, thanh dài nhất là 30m, thanh ngắn nhất là 6m; tính chiều dài của thanh cách điểm giữa cầu 18m. Bài 6 trang 71 Toán lớp 10 Tập 2

Hoạt động khởi động trang 63 Toán lớp 10 Tập 2
Hoạt động khởi động trang 63 Toán lớp 10 Tập 2: Nếu cắt mặt nón tròn xoay bởi mặt phẳng vuông góc với trục và không đi qua đỉnh của các mặt nón thì ta thu được một đường tròn (C).
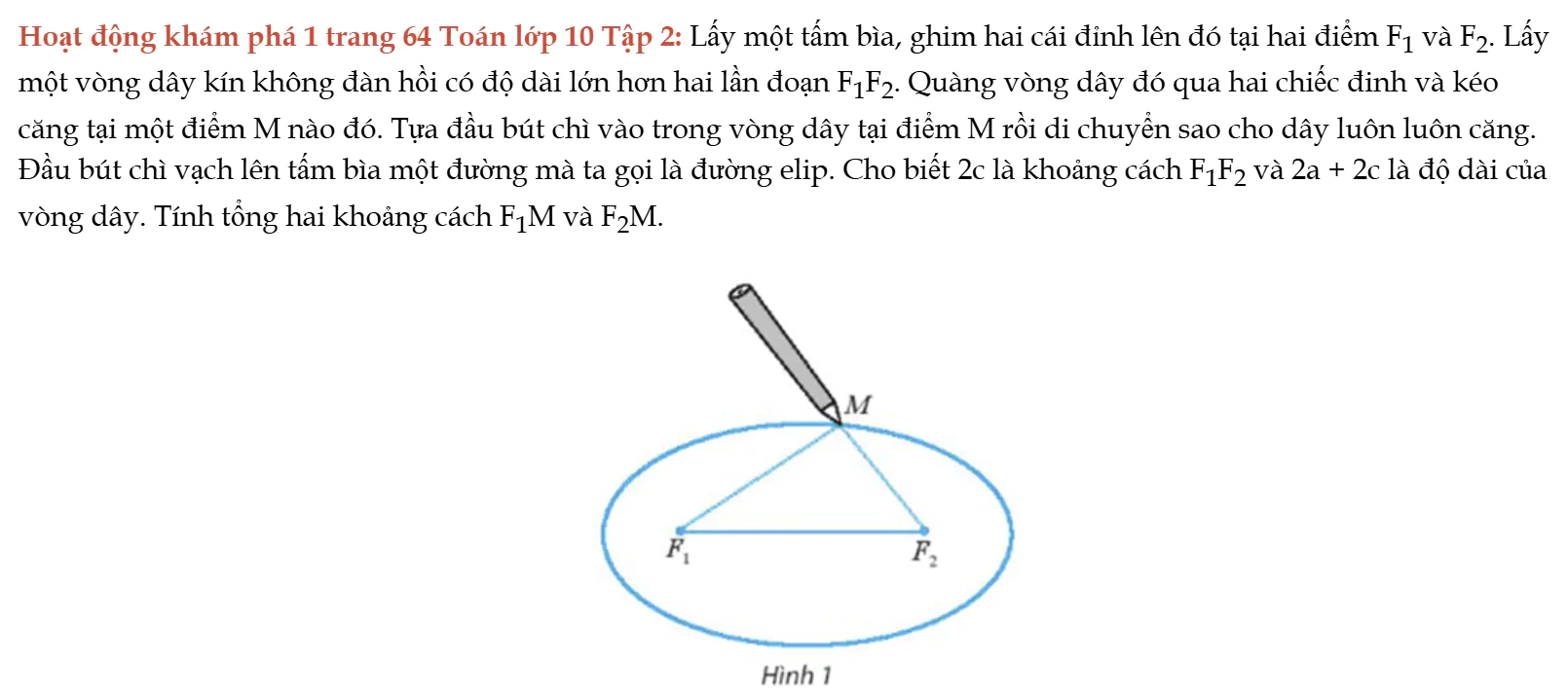
Hoạt động khám phá 1 trang 64 Toán lớp 10 Tập 2
Hoạt động khám phá 1 trang 64 Toán lớp 10 Tập 2

Hoạt động khám phá 2 trang 64 Toán lớp 10 Tập 2
Hoạt động khám phá 2 trang 64 Toán lớp 10 Tập 2

Hoạt động khám phá 3 trang 65 Toán lớp 10 Tập 2
Hoạt động khám phá 3 trang 65 Toán lớp 10 Tập 2
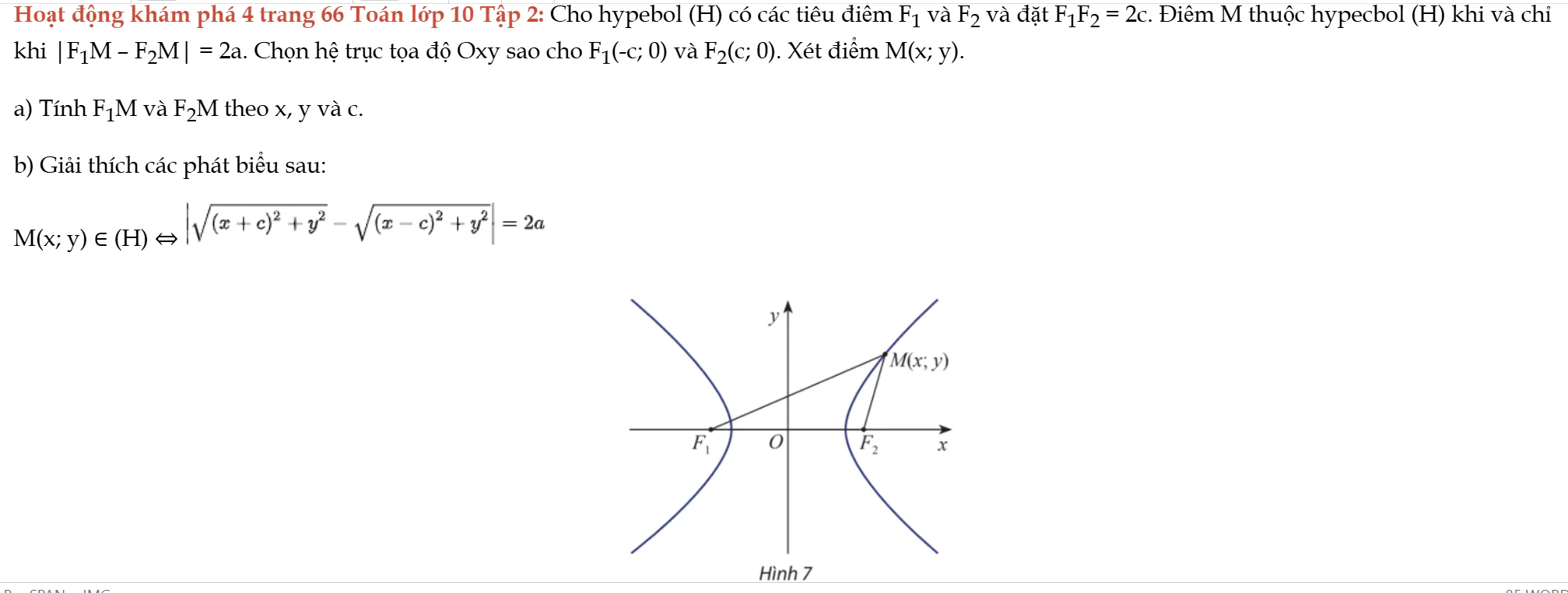
Hoạt động khám phá 4 trang 66 Toán lớp 10 Tập 2
Hoạt động khám phá 4 trang 66 Toán lớp 10 Tập 2

Hoạt động khám phá 5 trang 68 Toán lớp 10 Tập 2
Hoạt động khám phá 5 trang 68 Toán lớp 10 Tập 2
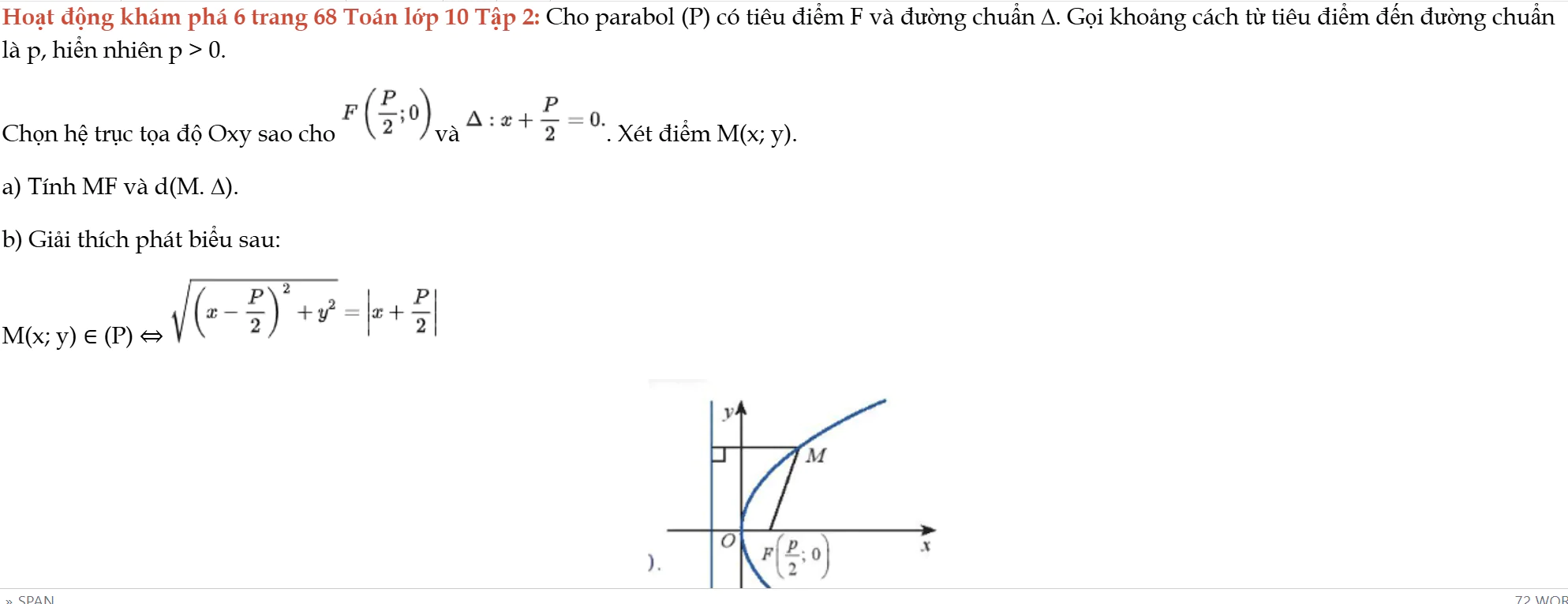
Hoạt động khám phá 6 trang 68 Toán lớp 10 Tập 2
Hoạt động khám phá 6 trang 68 Toán lớp 10 Tập 2: Cho parabol (P) có tiêu điểm F và đường chuẩn ∆. Gọi khoảng cách từ tiêu điểm đến đường chuẩn là p, hiển nhiên p > 0.
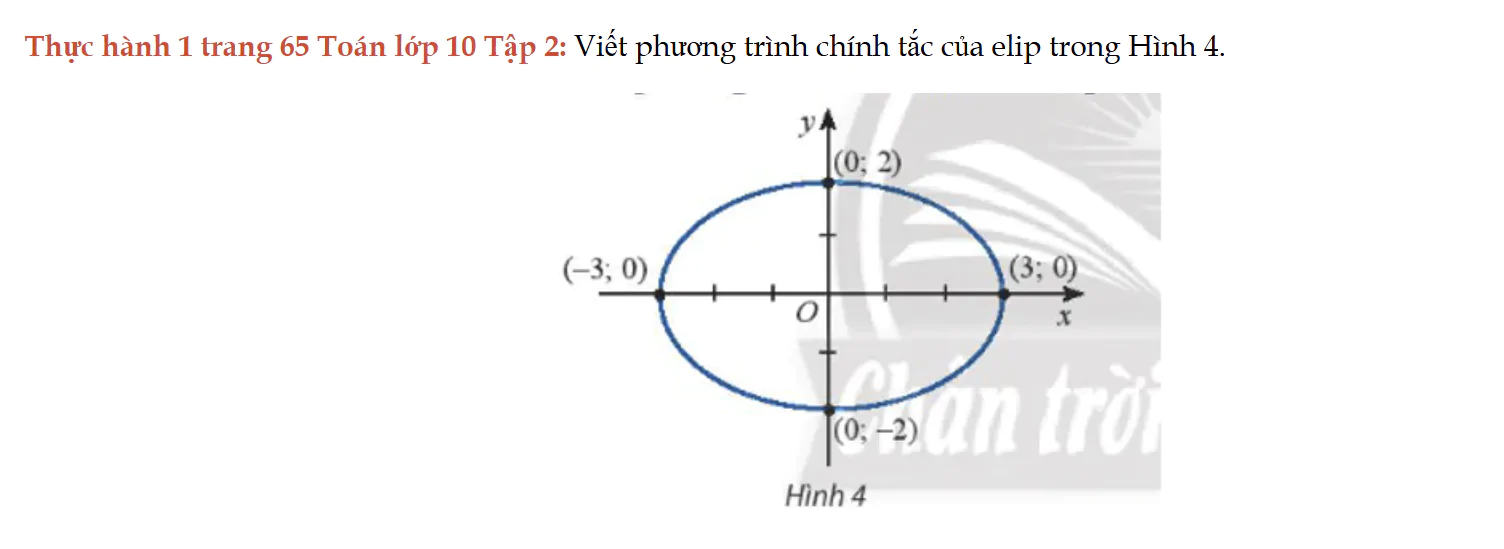
Thực hành 1 trang 65 Toán lớp 10 Tập 2
Thực hành 1 trang 65 Toán lớp 10 Tập 2: Viết phương trình chính tắc của elip trong Hình 4.

Thực hành 2 trang 67 Toán lớp 10 Tập 2
Thực hành 2 trang 67 Toán lớp 10 Tập 2: Viết phương trình chính tắc của hypebol có tiêu cự bằng 10 và độ dài trục ảo bằng 6.

Thực hành 3 trang 70 Toán lớp 10 Tập 2
Thực hành 3 trang 70 Toán lớp 10 Tập 2: Viết phương trình chính tắc của parabol (P) có đường chuẩn

Vận dụng 1 trang 65 Toán lớp 10 Tập 2
Một đường hầm có mặt cắt hình nửa elip cao 4m, rộng 10m (Hình 5). Viết phương trình chính tắc của elip đó. Vận dụng 1 trang 65 Toán lớp 10 Tập 2

Vận dụng 2 trang 67 Toán lớp 10 Tập 2
Một tháp làm nguội của một nhà máy có mặt cắt là một hypebol có phương trình sau (Hình 9). Vận dụng 2 trang 67 Toán lớp 10 Tập 2

Vận dụng 3 trang 70 Toán lớp 10 Tập 2
Một cổng chào có hình parabol cao 10m và bề rộng của cổng tại chân cổng là 5m. Tính bề rộng của cổng tại chỗ cách đỉnh 2m. Vận dụng 3 trang 70 Toán lớp 10 Tập 2
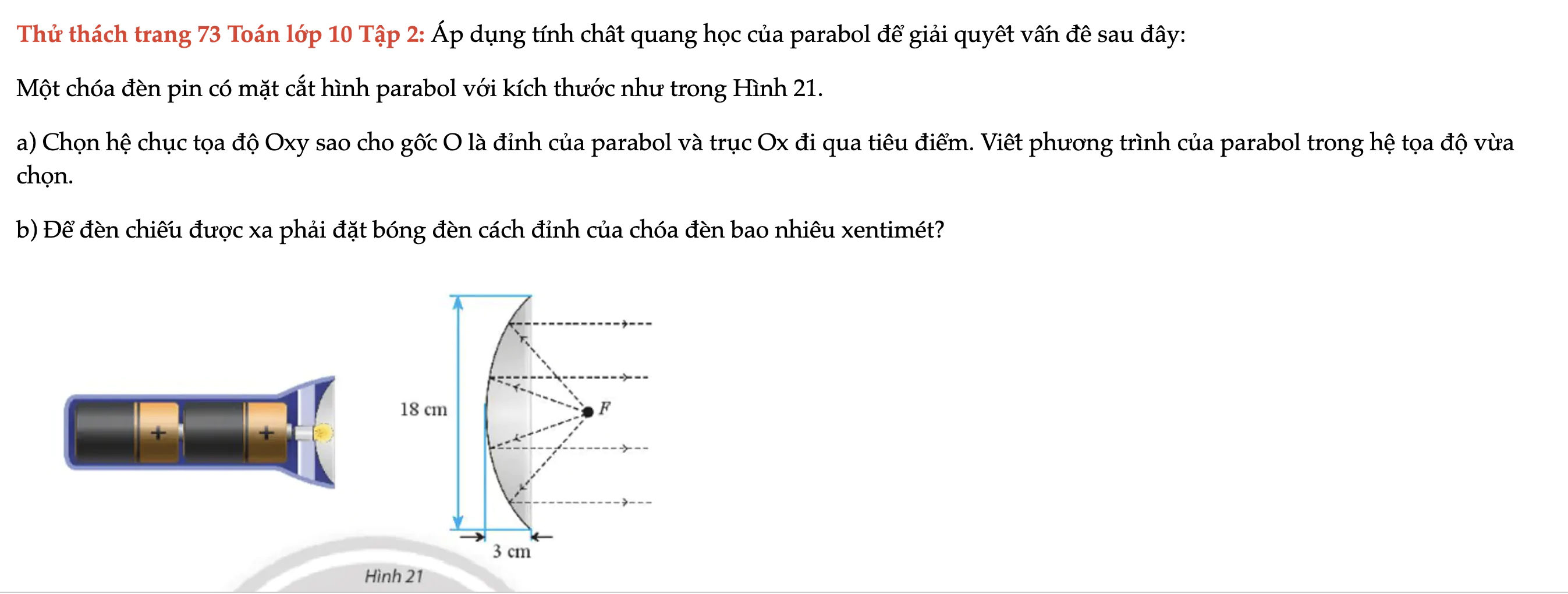
Thử thách trang 73 Toán lớp 10 Tập 2
Áp dụng tính chất quang học của parabol để giải quyết vấn đề sau đây. Một chóa đèn pin có mặt cắt hình parabol với kích thước như trong Hình 21. Thử thách trang 73 Toán lớp 10 Tập 2
Giải bài tập Bài tập cuối chương 9

Bài 1 trang 73 Toán lớp 10 Tập 2
Trong mặt phẳng Oxy, cho bốn điểm A(2; 1), B(1; 4), C(4; 5), D(5; 2); chứng minh ABCD là một hình vuông. Bài 1 trang 73 Toán lớp 10 Tập 2

Bài 2 trang 73 Toán lớp 10 Tập 2
Cho AB và CD là hai dây cung vuông góc tại E của đường tròn (O); vẽ hình chữ nhật AECF; dùng phương pháp tọa độ để chứng minh EF vuông góc với DB. Bài 2 trang 73 Toán lớp 10 Tập 2

Bài 3 trang 73 Toán lớp 10 Tập 2
Tìm tọa độ giao điểm và góc giữa hai đường thẳng d1 và d2 trong mỗi trường hợp; d1: x – y + 2 = 0 và d2: x + y + 4 = 0. Bài 3 trang 73 Toán lớp 10 Tập 2
Bài 4 trang 74 Toán lớp 10 Tập 2
Tính tâm và bán kính của đường tròn tâm M(-2; 3) và tiếp xúc với đường thẳng d: 14x – 5y + 60 = 0. Bài 4 trang 74 Toán lớp 10 Tập 2
Bài 5 trang 74 Toán lớp 10 Tập 2
Tính khoảng cách giữa hai đường thẳng: ∆: 6x + 8y – 13 = 0 và ∆’: 3x + 4y – 27 = 0. Bài 5 trang 74 Toán lớp 10 Tập 2

Bài 6 trang 74 Toán lớp 10 Tập 2
Tìm tâm và bán kính của các đường tròn có phương trình. Bài 6 trang 74 Toán lớp 10 Tập 2

Bài 7 trang 74 Toán lớp 10 Tập 2
Lập phương trình đường tròn trong các trường hợp sau. Bài 7 trang 74 Toán lớp 10 Tập 2
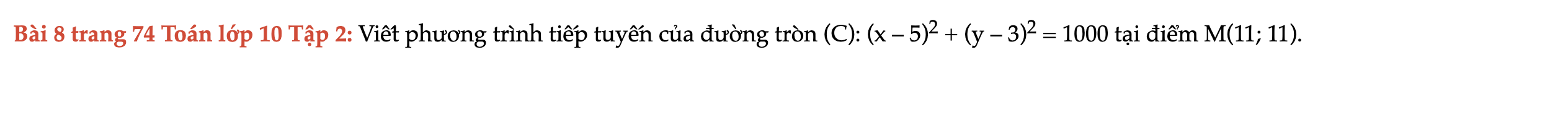
Bài 8 trang 74 Toán lớp 10 Tập 2
Viết phương trình tiếp tuyến của đường tròn (C). Bài 8 trang 74 Toán lớp 10 Tập 2

Bài 9 trang 74 Toán lớp 10 Tập 2
Tìm tọa độ các tiêu điểm, tọa độ các đỉnh, độ dài trục lớn và trục nhỏ của các elip. Bài 9 trang 74 Toán lớp 10 Tập 2

Bài 10 trang 74 Toán lớp 10 Tập 2
Viết phương trình chính tắc của elip thỏa mãn từng điều kiện đỉnh (5; 0), (0; 4). Bài 10 trang 74 Toán lớp 10 Tập 2

Bài 11 trang 74 Toán lớp 10 Tập 2
Tìm tọa độ các tiêu điểm, tọa độ các đỉnh, độ dài trục thực và trục ảo của các hypebol. Bài 11 trang 74 Toán lớp 10 Tập 2

Bài 12 trang 74 Toán lớp 10 Tập 2
Viết phương trình chính tắc của hypebol thỏa mãn từng điều kiện đỉnh (3; 0), tiêu điểm (5; 0). Bài 12 trang 74 Toán lớp 10 Tập 2

Bài 13 trang 74 Toán lớp 10 Tập 2
Tìm tọa độ tiêu điểm, phương trình đường chuẩn của các parabol. Bài 13 trang 74 Toán lớp 10 Tập 2

Bài 14 trang 74 Toán lớp 10 Tập 2
Viết phương trình chính tắc của parabol thỏa mãn từng điều kiện tiêu điểm (4; 0). Bài 14 trang 74 Toán lớp 10 Tập 2

Bài 15 trang 74 Toán lớp 10 Tập 2
Một gương lõm có mặt cắt hình parabol như Hình 1, có tiêu điểm cách đỉnh 5cm, cho biết bề sâu của gương là 45 cm có tính khoảng cách AB. Bài 15 trang 74 Toán lớp 10 Tập 2

Bài 16 trang 75 Toán lớp 10 Tập 2
Một bộ thu năng lượng mặt trời để làm nóng nước được làm bằng một tấm thép không gỉ có mặt cắt hình parabol, nước sẽ chảy thông qua một đường ống nằm ở tiêu điểm của parabol; viết phương trình chính tắc của parabol. Bài 16 trang 75 Toán lớp 10 Tập 2

Bài 17 trang 75 Toán lớp 10 Tập 2
Cổng trào của một thành phố dạng hình parabol có khoảng cách giữa hai chân cổng là 192m, từ một điểm M trên thân cổng, người ta đo được khoảng cách đến mặt đất là 2m và khoảng cách từ chân đường vuông góc vẽ từ M xuống mặt đất đến cổng gần nhất là 0,5 m.

Bài 18 trang 75 Toán lớp 10 Tập 2
Một người đứng ở giữa một tấm ván gỗ đặt trên giàn giáo để sơn tường nhà, biết rằng giàn giáo dài 16 m và độ võng tại tâm của ván gỗ (điểm ở giữa ván gỗ) là 3cm, cho biết đường cong của ván gỗ có hình parabol. Bài 18 trang 75 Toán lớp 10 Tập 2