Giải bài tập Toán 9 Chương 9. Tứ giác nội tiếp. Đa giác đều | Chân trời sáng tạo
Hướng dẫn giải chi tiết Chương 9. Tứ giác nội tiếp. Đa giác đều. Đường tròn ngoại tiếp và đường tròn nội tiếp tam giác, tứ giác nội tiếp. Các đa giác đều, các phép quay giữ nguyên hình đa giác đều và ứng dụng thực tiễn
Giải bài tập Bài 1. Đường tròn ngoại tiếp tam giác. Đường tròn nội tiếp tam giác

Khởi động trang 65 Toán 9 Tập 2
Ba cụm dân cư A, B, C nối với nhau bởi ba con đường AB, BC, CA như hình dưới đây. Người ta muốn tìm địa điểm O để xây một trường học và địa điểm I cách đều ba con đường. Khởi động trang 65 Toán 9 Tập 2

Khám phá 1 trang 65 Toán 9 Tập 2
Cho ba điểm A, B, C không thẳng hàng. Gọi O là giao điểm của đường trung trực của đoạn thẳng AB và BC (Hình 1). Khám phá 1 trang 65 Toán 9 Tập 2

Thực hành 1 trang 67 Toán 9 Tập 2
Xác định tâm và bán kính của đường tròn ngoại tiếp mỗi tam giác sau. Thực hành 1 trang 67 Toán 9 Tập 2

Vận dụng 1 trang 67 Toán 9 Tập 2
Có ba tổ dựng lều ở ba vị trí A, B, C như Hình 6. Ban tổ chức đặt ba thùng có dung tích bằng nhau tại một điểm tập kết chung. Vận dụng 1 trang 67 Toán 9 Tập 2

Khám phá 2 trang 67 Toán 9 Tập 2
Gọi I là giao điểm ba đường phân giác của tam giác ABC. Vẽ ID, IE, IF lần lượt vuông góc với các cạnh BC, AC và AB (Hình 7). Khám phá 2 trang 67 Toán 9 Tập 2
Thực hành 2 trang 68 Toán 9 Tập 2
Xác định tâm và bán kính đường tròn nội tiếp tam giác đều MNP có độ dài cạnh bằng 8 cm. Thực hành 2 trang 68 Toán 9 Tập 2
Vận dụng 2 trang 68 Toán 9 Tập 2
Theo gợi ý trong Hình 10, nêu cách xác định hai điểm I và O của tình huống trong Hoạt động khởi động (trang 65). Vận dụng 2 trang 68 Toán 9 Tập 2

Bài 1 trang 68 Toán 9 Tập 2
Cho tam giác đều ABC có cạnh bằng 6 cm. Bài 1 trang 68 Toán 9 Tập 2

Bài 2 trang 69 Toán 9 Tập 2
Cho tam giác ABC (AC < BC) nội tiếp đường tròn (O) có AB là đường kính. Từ điểm O vẽ đường thẳng song song với AC và cắt đường tròn (O) tại I (điểm I thuộc cung nhỏ CB). Bài 2 trang 69 Toán 9 Tập 2

Bài 3 trang 69 Toán 9 Tập 2
Cho tam giác ABC ngoại tiếp đường tròn (I). Gọi D, E, F lần lượt là các tiếp điểm của đường tròn (I) với các cạnh AB, BC, AC (Hình 11). Bài 3 trang 69 Toán 9 Tập 2

Bài 4 trang 69 Toán 9 Tập 2
Tính diện tích tam giác đều có bán kính đường tròn nội tiếp bằng 1 cm. Bài 4 trang 69 Toán 9 Tập 2

Bài 5 trang 69 Toán 9 Tập 2
Một trại nuôi gia súc có dạng hình tam giác đều cạnh 100 m (Hình 12). Người ta muốn đặt một trụ đèn cao áp tại một điểm cách đều ba đỉnh của tam giác. Bài 5 trang 69 Toán 9 Tập 2
Giải bài tập Bài 2. Tứ giác nội tiếp

Khởi động trang 70 Toán 9 Tập 2
Quan sát hai hình tứ giác ABCD và A'B'C'D', hãy nêu nhận xét sự khác biệt về vị trí của mỗi hình đối với đường tròn trong hình đó. Khởi động trang 70 Toán 9 Tập 2

Khám phá 1 trang 70 Toán 9 Tập 2
Các tứ giác trong Hình 1 có đặc điểm gì giống nhau? Khám phá 1 trang 70 Toán 9 Tập 2
Thực hành 1 trang 71 Toán 9 Tập 2
Vẽ một tứ giác nội tiếp hình tròn và một tứ giác không nội tiếp đường tròn. Thực hành 1 trang 71 Toán 9 Tập 2

Vận dụng 1 trang 71 Toán 9 Tập 2
Có nhận xét gì về tứ giác trong hình hoa văn trang trí mặt lưng của chiếc ghế với đường tròn trong Hình 3. Vận dụng 1 trang 71 Toán 9 Tập 2

Khám phá 2 trang 71 Toán 9 Tập 2
Cho tứ giác ABCD nội tiếp đường tròn (O) (Hình 4). Khám phá 2 trang 71 Toán 9 Tập 2

Thực hành 2 trang 71 Toán 9 Tập 2
Tìm số đo các góc chưa biết của tứ giác ABCD trong Hình 6. Thực hành 2 trang 71 Toán 9 Tập 2

Vận dụng 2 trang 71 Toán 9 Tập 2
Trong hình vẽ minh họa của học sinh có một tứ giác ABCD nội tiếp đường tròn tâm O (Hình 7). Vận dụng 2 trang 71 Toán 9 Tập 2

Khám phá 3 trang 72 Toán 9 Tập 2
Cho hình chữ nhật ABCD và hình vuông MNPQ (Hình 8). Khám phá 3 trang 72 Toán 9 Tập 2

Thực hành 3 trang 73 Toán 9 Tập 2
Xác định tâm và bán kính của đường tròn ngoại tiếp hình vuông và hình chữ nhật trong Hình 11. Thực hành 3 trang 73 Toán 9 Tập 2

Vận dụng 3 trang 73 Toán 9 Tập 2
Một người muốn thiết kế một bảng hiệu gồm một hình vuông nội tiếp một đường tròn bán kính R = 3 cm (Hình 12). Tính diện tích hình vuông đó. Vận dụng 3 trang 73 Toán 9 Tập 2

Bài 2 trang 74 Toán 9 Tập 2
Cho tam giác nhọn ABC. Gọi A', B', C' lần lượt là chân đường cao kẻ từ A, B, C và H là trực tâm của tam giác đó. Hãy chỉ ra các tứ giác nội tiếp có trong hình. Bài 2 trang 74 Toán 9 Tập 2
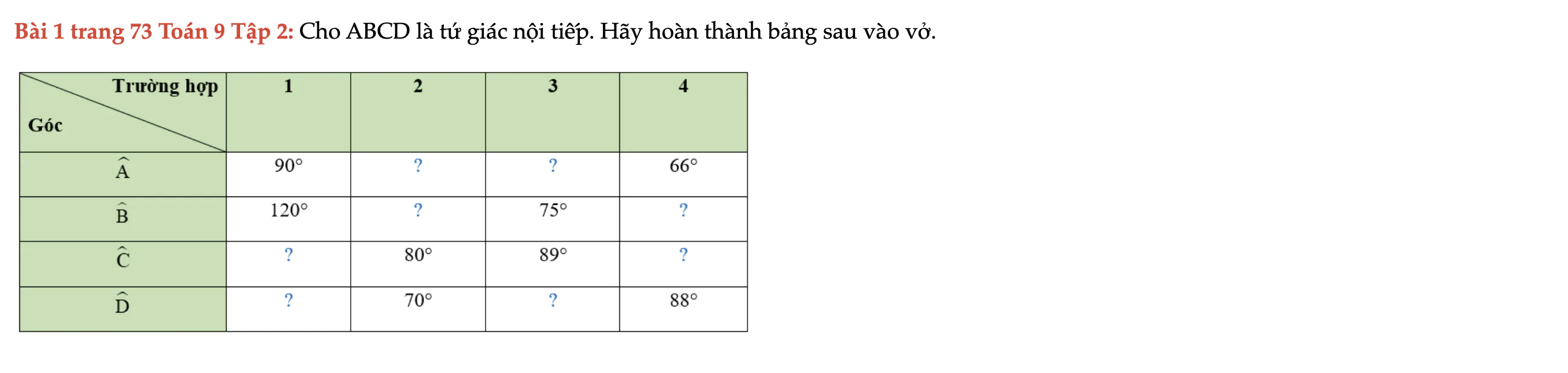
Bài 1 trang 73 Toán 9 Tập 2
Cho ABCD là tứ giác nội tiếp. Hãy hoàn thành bảng sau vào vở. Bài 1 trang 73 Toán 9 Tập 2

Bài 3 trang 74 Toán 9 Tập 2
Xác định tâm và bán kính đường tròn ngoại tiếp hình chữ nhật ABCD trong mỗi trường hợp sau. Bài 3 trang 74 Toán 9 Tập 2

Bài 4 trang 74 Toán 9 Tập 2
Cho hình vuông MNPQ nội tiếp đường tròn bán kính R. Tính độ dài cạnh và đường chéo của hình vuông theo R. Bài 4 trang 74 Toán 9 Tập 2

Bài 5 trang 74 Toán 9 Tập 2
Từ một điểm M nằm ngoài đường tròn (O), vẽ cát tuyến MBC và tiếp tuyến Mt tiếp xúc với (O) tại A. Gọi I là trung điểm của dây BC. Chứng minh AMIO là một tứ giác nội tiếp. Bài 5 trang 74 Toán 9 Tập 2

Bài 6 trang 74 Toán 9 Tập 2
Cho tam giác ABC vuông tại A. Lấy điểm M bất kì trên đoạn AC, đường tròn đường kính CM cắt hai đường thẳng BM và BC lần lượt tại D và N. Bài 6 trang 74 Toán 9 Tập 2

Bài 7 trang 74 Toán 9 Tập 2
Cho hình vuông ABCD có độ dài cạnh bằng a. Góc vuông xAy thay đổi sao cho tia Ax cắt đoạn thẳng BC tại M và tia Ay cắt đoạn thẳng CD kéo dài tại N. Bài 7 trang 74 Toán 9 Tập 2
Giải bài tập Bài 3. Đa giác đều và phép quay

Khởi động trang 75 Toán 9 Tập 2
Khởi động trang 75 Toán 9 Tập 2

Khám phá 1 trang 75 Toán 9 Tập 2
Có nhận xét gì về cạnh và góc của mỗi đa giác sau? Khám phá 1 trang 75 Toán 9 Tập 2

Thực hành 1 trang 77 Toán 9 Tập 2
Cho đường tròn (O; R), trên đó lấy các điểm M, N, P, Q, R sao cho số đo các cung MN, NP, PQ, QR, RM bằng nhau. Đa giác MNPQR có là đa giác đều không? Vì sao? Thực hành 1 trang 77 Toán 9 Tập 2
Vận dụng 1 trang 77 Toán 9 Tập 2
Cho lục giác đều ABCDEF có M, N, P, Q, R, S lần lượt là trung điểm của các cạnh AB, BC, DE, EF, FA. Đa giác MNPQRS có là đa giác đều không? Vì sao? Vận dụng 1 trang 77 Toán 9 Tập 2

Khám phá 2 trang 77 Toán 9 Tập 2
Vẽ hình vuông ABCD tâm O (Hình 5a). Cắt một tấm bìa hình vuông (gọi là ℋ) cùng độ dài cạnh với hình vuông ABCD (Hình 5b). Khám phá 2 trang 77 Toán 9 Tập 2

Thực hành 2 trang 78 Toán 9 Tập 2
Tìm phép quay biến hình ngũ giác đều tâm I thành chính nó (Hình 8). Thực hành 2 trang 78 Toán 9 Tập 2

Vận dụng 2 trang 78 Toán 9 Tập 2
Một vòng quay may mắn có dạng hình đa giác đều 10 cạnh (Hình 9). Tìm các phép quay biến đa giác này thành chính nó. Vận dụng 2 trang 78 Toán 9 Tập 2

Thực hành 3 trang 79 Toán 9 Tập 2
Em hãy tìm một số hình phẳng đều trong thực tế. Thực hành 3 trang 79 Toán 9 Tập 2
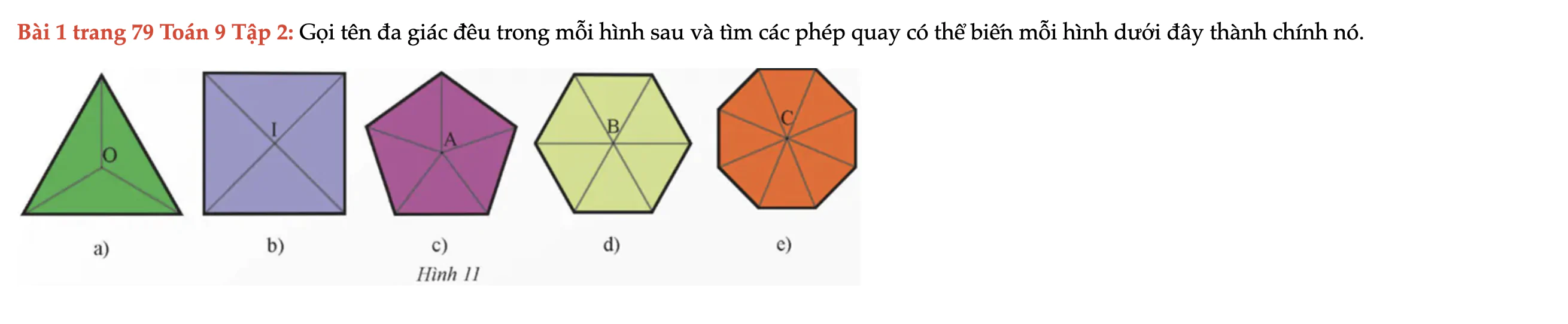
Bài 1 trang 79 Toán 9 Tập 2
Gọi tên đa giác đều trong mỗi hình sau và tìm các phép quay có thể biến mỗi hình dưới đây thành chính nó. Bài 1 trang 79 Toán 9 Tập 2

Bài 2 trang 79 Toán 9 Tập 2
Cho đa giác đều 9 cạnh có tâm O và AB, BC là hai cạnh đa giác (Hình 12). Bài 2 trang 79 Toán 9 Tập 2

Bài 3 trang 80 Toán 9 Tập 2
Đường viền ngoài của chiếc đồng hồ trong Hình 13 được làm theo hình đa giác đều nào? Tìm phép quay biến đa giác này thành chính nó. Bài 3 trang 80 Toán 9 Tập 2

Bài 4 trang 80 Toán 9 Tập 2
Cho đường tròn (O; R). Vẽ hình tam giác đều, hình vuông, hình lục giác đều có các đỉnh nằm trên (O; R). Tính các cạnh của các hình vừa vẽ theo R. Bài 4 trang 80 Toán 9 Tập 2

Bài 5 trang 80 Toán 9 Tập 2
Tìm các hình phẳng có tính đều trong tự nhiên; trong sản xuất, thiết kế, mĩ thuật. Bài 5 trang 80 Toán 9 Tập 2

Bài 6 trang 80 Toán 9 Tập 2
Vòng trong của mái giếng trời hình hoa sen của nhà ga Bến Thành (Thành phố Hồ Chí Minh) có dạng đa giác đều 12 cạnh (Hình 14). Bài 6 trang 80 Toán 9 Tập 2
Giải bài tập Bài tập cuối chương 9

Bài 1 trang 81 Toán 9 Tập 2
Cho tam giác đều ABC có đường cao AH = 9 cm. Bán kính r của đường tròn nội tiếp tam giác có độ dài là. Bài 1 trang 81 Toán 9 Tập 2

Bài 2 trang 81 Toán 9 Tập 2
Cho tam giác ABC có AB = AC = 4 cm. Bán kính R của đường tròn ngoại tiếp tam giác có độ dài là. Bài 2 trang 81 Toán 9 Tập 2
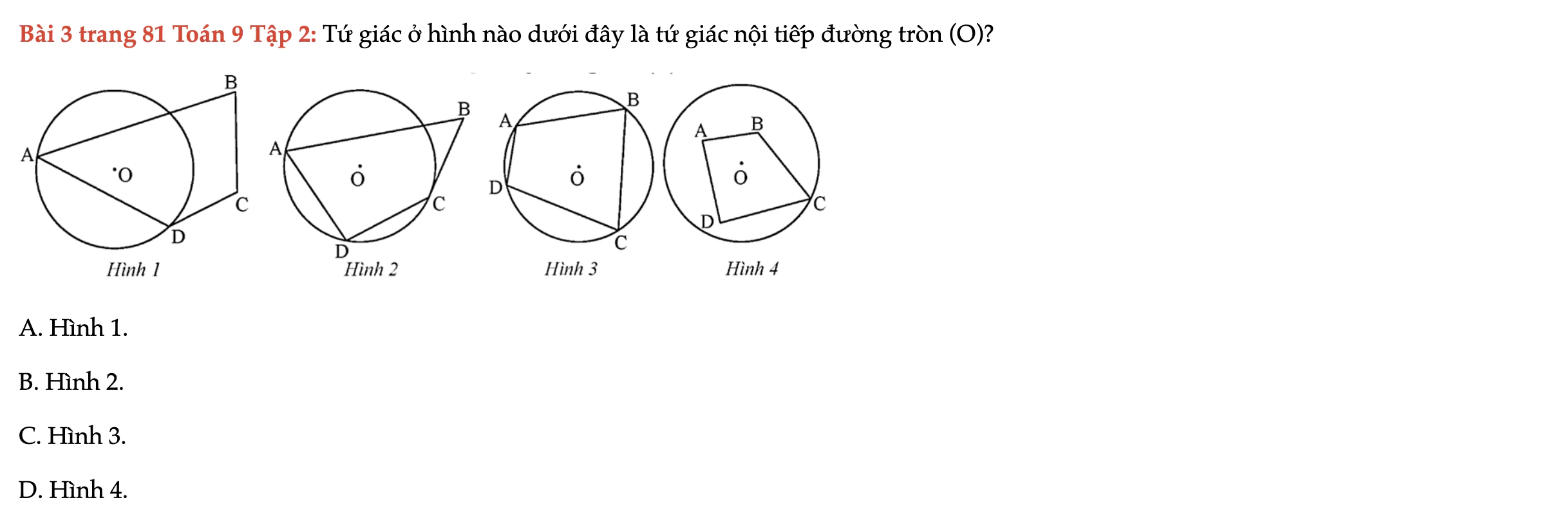
Bài 3 trang 81 Toán 9 Tập 2
Tứ giác ở hình nào dưới đây là tứ giác nội tiếp đường tròn (O)? Bài 3 trang 81 Toán 9 Tập 2

Bài 4 trang 81 Toán 9 Tập 2
Trong các phát biểu sau, phát biểu nào đúng? Bài 4 trang 81 Toán 9 Tập 2

Bài 5 trang 81 Toán 9 Tập 2
Cho tứ giác MNPQ nội tiếp đường tròn (O; R) và góc M = 60°. Số đo góc của góc P là. Bài 5 trang 81 Toán 9 Tập 2

Bài 6 trang 81 Toán 9 Tập 2
Cho tứ giác ABCD nội tiếp đường tròn (O). Biết góc DAO = 50°; OCD = 30°. Bài 6 trang 81 Toán 9 Tập 2

Bài 7 trang 81 Toán 9 Tập 2
Cho tứ giác ABDC nội tiếp có góc ACD = 60°. Khẳng định nào sau đây luôn đúng? Bài 7 trang 81 Toán 9 Tập 2

Bài 8 trang 82 Toán 9 Tập 2
Cho lục giác đều ABCDEF nội tiếp đường tròn bán kính R. Độ dài cạnh AB bằng. Bài 8 trang 82 Toán 9 Tập 2

Bài 9 trang 82 Toán 9 Tập 2
Cho tam giác đều ABC có O là tâm đường tròn ngoại tiếp. Phép quay nào với O là tâm biến tam giác ABC thành chính nó? Bài 9 trang 82 Toán 9 Tập 2

Bài 10 trang 82 Toán 9 Tập 2
Cho tam giác nhọn ABC có đường cao AH (H ∈ BC) và nội tiếp đường tròn tâm O có đường kính AM (hình 6). Chứng minh góc OAC = góc BAH. Bài 10 trang 82 Toán 9 Tập 2

Bài 11 trang 82 Toán 9 Tập 2
Cho tam giác ABC vuông tại A (AB < AC) có AH là đường cao. Lần lượt vẽ đường tròn (O) đường kính BH và đường tròn (O') đường kính HC. Bài 11 trang 82 Toán 9 Tập 2

Bài 12 trang 82 Toán 9 Tập 2
Mái nhà trong Hình 7 được đỡ bởi khung đa giác đều. Gọi tên đa giác đó. Tìm phép quay biến đa giác đó thành chính nó. Bài 12 trang 82 Toán 9 Tập 2