Giải bài tập Toán 9 Bài 1. Bất đẳng thức. | Chân trời sáng tạo
Hướng dẫn giải chi tiết Bài 1. Bất đẳng thức. Khái niệm và tính chất bất đẳng thức
Bài 1 trang 28 Toán 9 Tập 1
Bài 1 trang 28 Toán 9 Tập 1: Dùng các dấu >, <, ≥, ≤ để diễn tả:
a) Tốc độ v đúng quy định với biển báo giao thông ở Hình 4a.
b) Trọng tải P của toàn bộ xe khi đi qua cầu đúng quy định với biển báo giao thông ở Hình 4b.

Bài 2 trang 29 Toán 9 Tập 1
Bài 2 trang 29 Toán 9 Tập 1: Hãy chỉ ra các bất đẳng thức diễn tả mỗi khẳng định sau:
a) m lớn hơn 8;
b) n nhỏ hơn 21;
c) x nhỏ hơn hoặc bằng 4;
d) y lớn hơn hoặc bằng 0.
Bài 3 trang 29 Toán 9 Tập 1
Bài 3 trang 29 Toán 9 Tập 1: Hãy cho biết các bất đẳng thức được tạo thành khi:
a) Cộng hai vế của bất đẳng thức  với −4;
với −4;
b) Cộng hai vế của bất đẳng thức  với 9;
với 9;
c) Nhân hai vế của bất đẳng thức  với 3, rồi tiếp tục cộng với 2;
với 3, rồi tiếp tục cộng với 2;
d) Cộng hai vế của bất đẳng thức  với −1, rồi tiếp tục cộng với −7.
với −1, rồi tiếp tục cộng với −7.
Bài 4 trang 29 Toán 9 Tập 1
Bài 4 trang 29 Toán 9 Tập 1: So sánh hai số x và y trong mỗi trường hợp sau:
a)  ;
;
b)  ;
;
c)  ;
;
d)  .
.
Bài 5 trang 29 Toán 9 Tập 1
Bài 5 trang 29 Toán 9 Tập 1: Cho hai số a, b thỏa mãn a < b. Chứng tỏ:
a)  ;
;
b)  ;
;
c)  ;
;
d) 
Khởi động trang 25 Toán 9 Tập 1
Theo quy định của một hãng bay, khối lượng hành lí xách tay của khách hàng phổ thông không được vượt quá 12 kg. Gọi m là khối lượng hành lí xách tay của một khách hàng phổ thông. Hệ thức nào biểu diễn khối lượng hành lí đúng quy định của hãng bay?

Khám phá 1 trang 25 Toán 9 Tập 1
Cho hai số thực x và y được biểu diễn trên trục số (Hình 1).
Hãy cho biết số nào lớn hơn.

Thực hành 1 trang 26 Toán 9 Tập 1
Hãy chỉ ra các bất đẳng thức diễn tả mỗi khẳng định sau:
a) x nhỏ hơn 5;
b) a không lớn hơn b;
c) m không nhỏ hơn n.
Khám phá 2 trang 26 Toán 9 Tập 1
Cho a, b, c là ba số thỏa mãn a > b và b > c. Trong hai số a và c, số nào lớn hơn? Vì sao?

Khám phá 3 trang 26 Toán 9 Tập 1
Thay mỗi ? sau bằng dấu thích hợp (>, <):
a) 4 > 1
![]() b) −10 < −5
b) −10 < −5
![]()
Thực hành 4 trang 27 Toán 9 Tập 1
Cho hai số m và n thỏa mãn m > n. Chứng tỏ m + 5 > n + 4.
Vận dụng 1 trang 27 Toán 9 Tập 1
Gọi a là số tuổi của bạn Na, b là số tuổi của bạn Toàn, biết rằng bạn Toàn lớn tuổi hơn bạn Na. Hãy dùng bất đẳng thức để biểu diễn mối quan hệ về tuổi của hai bạn đó ở hiện tại và sau ba năm nữa.
Khám phá 4 trang 27 Toán 9 Tập 1
Thay mỗi ? sau bằng dấu thích hợp (>, <):
a) 3 > 2
![]()
b) -10 < -2
![]()
c) 5 > 3
![]()
d) -10 < -2
![]()
Đố vui trang 29 Toán 9 Tập 1
Tìm lỗi sai trong lập luận sau:
Bạn Trang nhỏ tuổi hơn bạn Mai, bạn Mai nhẹ cân hơn bạn Tín. Gọi a và b lần lượt là số tuổi của bạn Trang và bạn Mai; b và c là số cân nặng của bạn Mai và bạn Tín. Vì a < b và b < c nên theo tính chất bắc cầu ta suy ra a < c. Vậy bạn Trang nhỏ tuổi hơn bạn Tín.
 và
và  .
. và
và  .
. và
và 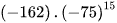
 . Chứng tỏ
. Chứng tỏ 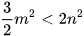 .
. , hãy so sánh m và n.
, hãy so sánh m và n.