Giải bài tập Bài 11 trang 82 Toán 9 Tập 2 | Toán 9 - Chân trời sáng tạo
Hướng dẫn giải chi tiết từng bước bài tập Bài 11 trang 82 Toán 9 Tập 2. Bài tập cuối chương 9. Toán 9 - Chân trời sáng tạo
Đề bài:
Cho tam giác ABC vuông tại A (AB < AC) có AH là đường cao. Lần lượt vẽ đường tròn (O) đường kính BH và đường tròn (O') đường kính HC.
a) Xét vị trí tương đối của hai đường tròn (O) và (O').
b) Đường tròn (O) cắt AB tại E, đường tròn (O') cắt AC tại F. Chứng minh rằng tứ giác AEHF là hình chữ nhật.
c) Chứng minh rằng EF là tiếp tuyến đường tròn (O) và đồng thời là tiếp tuyến đường tròn (O').
d) Đường trung tuyến AM của tam giác ABC cắt EF tại N. Cho biết AB = 6 cm, AC = 8 cm. Tính diện tích tam giác ANF.
Đáp án và cách giải chi tiết:
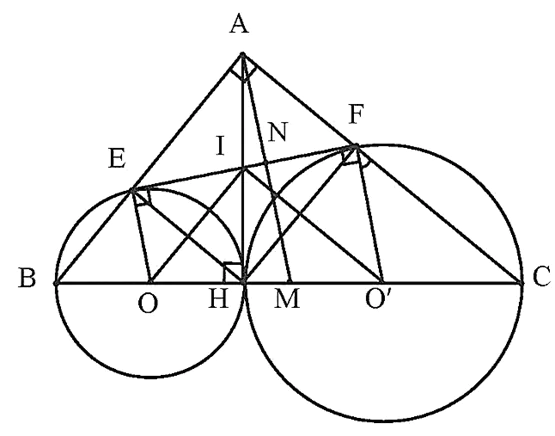
a) Đường tròn (O) có bán kính OH, đường tròn (O') có bán kính O'H.
Vì OO' = OH + HO' nên (O) và (O') tiếp xúc ngoài.
b) Ta có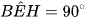 
(góc nội tiếp chắn nửa đường tròn (O)).
Suy ra HE ⊥ AB hay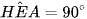 
Tương tự,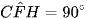 
(góc nội tiếp chắn nửa đường tròn (O')).
Suy ra HF ⊥ AC hay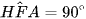 
Tứ giác AEHF có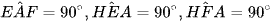 
Do đó, tứ giác AEHF là hình chữ nhật.
c) Gọi I là giao điểm AH và EF, ta có
IA = IE = IH = IF (tính chất hình chữ nhật).
• Xét ∆IEO và ∆IHO có: OI là cạnh chung; IE = IH; OE = OH.
Do đó ∆IEO = ∆IHO (c.c.c)
Suy ra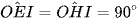 
(hai góc tương ứng).
Vì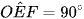 
và E thuộc đường tròn (O) nên EF là tiếp tuyến của (O). (1)
• Xét ∆IFO' và ∆IHO' có: O'I là cạnh chung; IF = IH; O'F = O'H.
Do đó ∆IFO' = ∆IHO' (c.c.c).
Suy ra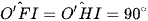 
(hai góc tương ứng).
Vì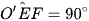 
và E thuộc đường tròn (O) nên EF là tiếp tuyến của (O). (2)
Từ (1) và (2) suy ra EF là tiếp tuyến của (O) và đồng thời là tiếp tuyến của (O').
d) Tam giác ABC vuông tại A có AM là đường trung tuyến.
Suy ra AM = BM = CM =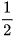 
BC.
Do đó ∆O'FC cân tại O' (vì O'F = O'C) suy ra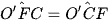 
Từ (3) và (4) suy ra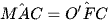 
Mà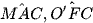 
là hai góc đồng vị nên AM // O'F).
Mặt khác O'F ⊥ EF, suy ra AM ⊥ EF tại N.
Xét tam giác ABC vuông tại A, áp dụng định lí Pythagore, ta có:
BC2 = AB2 + AC2.
Suy ra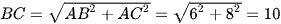 
(cm).
Diện tích tam giác ABC là:
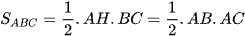
Suy ra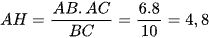 
(cm).
Do đó EF = AH = 4,8 cm.
• Vì ∆AHF ᔕ ∆ACH (g.g) nên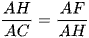 
Suy ra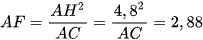 
(cm).
• Vì ∆AEF ᔕ ∆NAF (g.g) nên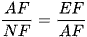 
Suy ra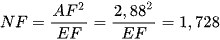 
(cm).
Xét tam giác AFN vuông tại A, áp dụng định lí Pythagore, ta có:
AF2 = AN2 + NF2.
Suy ra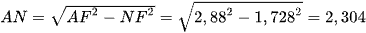 
(cm).
Diện tích tam giác AFN là:
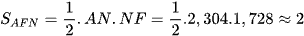(cm2).
Vậy diện tích tam giác ANF khoảng 2 cm2.
Nguồn: loigiaitoan.com
Tổng số đánh giá:
Xếp hạng: / 5 sao
Bài tập liên quan:
Bài 1 trang 81 Toán 9 Tập 2
Cho tam giác đều ABC có đường cao AH = 9 cm. Bán kính r của đường tròn nội tiếp tam giác có độ dài là
A. 6 cm.
B. 3 cm.
C. 4,5 cm.
D. 
cm.
Bài 2 trang 81 Toán 9 Tập 2
Cho tam giác ABC có AB = AC = 4 cm. Bán kính R của đường tròn ngoại tiếp tam giác có độ dài là
A.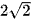 
cm.
B. 
cm.
C. 
cm.
D. 
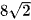cm.
Bài 3 trang 81 Toán 9 Tập 2
Tứ giác ở hình nào dưới đây là tứ giác nội tiếp đường tròn (O)?
A. Hình 1.
B. Hình 2.
C. Hình 3.
D. Hình 4.
Bài 4 trang 81 Toán 9 Tập 2
Trong các phát biểu sau, phát biểu nào đúng?
A. Mọi tứ giác luôn nội tiếp đường tròn.
B. Trong một tứ giác nội tiếp, tổng số đo hai góc đối nhau bằng 90°.
C. Tổng số đo hai góc đối của một tứ giác nội tiếp luôn bằng 180°.
D. Tất cả các hình thang đều là tứ giác nội tiếp.
Bài 5 trang 81 Toán 9 Tập 2
Cho tứ giác MNPQ nội tiếp đường tròn (O; R) và 
. Số đo góc củ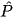a 
là
A. 30°.
B. 120°.
C. 180°.
D. 90°.
Bài 6 trang 81 Toán 9 Tập 2
Cho tứ giác ABCD nội tiếp đường tròn (O). Biết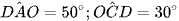 
(Hình 5).
Số đo củ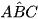a 
là
A. 80°.
B. 90°.
C. 100°.
D. 110°.
Bài 7 trang 81 Toán 9 Tập 2
Cho tứ giác ABDC nội tiếp có 
. Khẳng định nào sau đây luôn đúng?
A.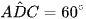 
B.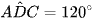 
C. 
D. 
Bài 8 trang 82 Toán 9 Tập 2
Cho lục giác đều ABCDEF nội tiếp đường tròn bán kính R. Độ dài cạnh AB bằng
A. R.
B. 
C.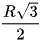 
D. 
Bài 9 trang 82 Toán 9 Tập 2
Cho tam giác đều ABC có O là tâm đường tròn ngoại tiếp. Phép quay nào với O là tâm biến tam giác ABC thành chính nó?
A. 90°.
B. 100°.
C. 110°.
D. 120°.
Bài 10 trang 82 Toán 9 Tập 2
Cho tam giác nhọn ABC có đường cao AH (H ∈ BC) và nội tiếp đường tròn tâm O có đường kính AM (hình 6). Chứng minh 
Bài 12 trang 82 Toán 9 Tập 2
Mái nhà trong Hình 7 được đỡ bởi khung đa giác đều. Gọi tên đa giác đó. Tìm phép quay biến đa giác đó thành chính nó.
